13. Квантовая головоломка. Массовая щель

В нескольких километрах к северу от Женевы граница между Швейцарией и Францией делает резкий изгиб. На поверхности в этом месте видны лишь проселочные дороги и небольшие деревеньки. Но под землей, на глубине от 50 до 175 м, находится самый крупный на планете научный прибор. Это гигантский кольцевой туннель более 8 км в диаметре, соединенный с другим, меньшим (примерно вчетверо) туннелем. Большая его часть находится под территорией Франции, но две секции приходятся на Швейцарию. По туннелям проложено по паре труб, которые сходятся в четырех точках.

Это Большой адронный коллайдер стоимостью €7,5 млрд (около $9 млрд). С его помощью ученые ведут исследования на переднем крае физики элементарных частиц. Ключевой целью 10 000 ученых более чем из 100 стран, вместе работающих на этой экспериментальной установке, было найти бозон Хиггса или не найти его, если так устроена Вселенная. Частица эта нужна была, чтобы дополнить Стандартную модель элементарных частиц, согласно которой все во Вселенной состоит из элементарных частиц 17 разновидностей. В теории бозон Хиггса — то, что придает всем частицам массу.

В декабре 2011 г. два основных детектора Большого адронного коллайдера — ATLAS и CMS — независимо друг от друга обнаружили предварительные свидетельства существования бозона Хиггса с массой около 125 ГэВ (гигаэлектронвольт — единица, которую в физике элементарных частиц используют для обозначения равно массы и энергии, поскольку то и другое эквивалентно). А 4 июля 2012 г. ЦЕРН — Европейский центр ядерных исследований, управляющий Большим адронным коллайдером, — объявил заинтересованной аудитории ученых и научных журналистов, что Вселенная высказалась в пользу Хиггса. Обе группы собрали большое количество дополнительных данных, и вероятность того, что данные показали случайную флуктуацию, а не присутствие новой частицы с хиггсовскими характеристиками, составляет теперь менее одной двухмиллионной. Именно такую степень уверенности традиционно требуют в физике элементарных частиц, прежде чем открывать шампанское.

Только дальнейшие эксперименты позволят с уверенностью сказать, обладает ли новая частица всеми теми свойствами, которые теоретически должны быть у бозона Хиггса. К примеру, теория предсказывает, что спин бозона Хиггса должен быть равен нулю, а на момент объявления наблюдаемые данные указывали на значение 0 либо 2. Может также оказаться, что «настоящий» бозон Хиггса состоит из других, меньших частиц или что это всего лишь первая ласточка из нового семейства хиггсоподобных частиц. В итоге либо существующая модель элементарных частиц будет подтверждена и закреплена, либо мы получим новую информацию, которая со временем позволит нам разработать другую, лучшую теорию.

Последняя из семи задач тысячелетия тесно связана со Стандартной моделью и бозоном Хиггса. Это центральный вопрос квантовой теории поля — математической области, в рамках которой изучается физика элементарных частиц. Его еще называют гипотезой «щели» в спектре масс, и он устанавливает конкретный нижний предел для возможной массы элементарной частицы. Это лишь одна репрезентативная задача, выбранная из целой серии крупных нерешенных вопросов в этой новейшей области математической физики, и она связана как с вопросами из самых передовых разделов чистой математики, так и с давней мечтой физиков — теорией, которая объединила бы две важнейшие физические теории: общую теорию относительности и квантовую теорию поля.

В классической ньютоновой механике фундаментальными физическими понятиями являются пространство, время и масса. Пространство считается трехмерным и евклидовым, время — одномерная величина, не зависящая от пространства, а масса указывает на присутствие вещества. Массы изменяют свое положение в пространстве под действием различных сил, и скорость, с которой меняется их положение, измеряется относительно времени. Ньютонов закон движения описывает, как ускорение тела (скорость изменения его скорости, которая, в свою очередь, отражает скорость изменения его позиции) соотносится с его массой и приложенной к нему силой.

Классические теории пространства, времени и вещества поднялись на максимальную высоту в уравнениях электромагнетизма, предложенных Джеймсом Максвеллом. Эта элегантная система уравнений объединила две силы природы, которые раньше рассматривались исключительно по отдельности. Оказалось, что вместо отдельных явлений электричества и магнетизма существует единое электромагнитное поле. Это поле пронизывает все пространство, как если бы Вселенная была наполнена какой-то невидимой жидкостью. В каждой точке пространства мы можем измерить величину и направление этого поля, как будто эта жидкость течет по математическим законам. Конечно, для некоторых целей электромагнитное поле можно разбить на два компонента, два поля: электрическое и магнитное. Но переменное магнитное поле порождает электрическое поле, и наоборот, так что, когда дело доходит до динамики, оба они должны рассматриваться совместно, как единое более сложное поле.

Эта удобная и уютная картина физического мира, в котором фундаментальные физические концепции описывали предметы и явления, воспринимаемые с помощью человеческих органов чувств, резко изменилась в самом начале XX в. Именно тогда физики начали понимать, что на очень маленьких масштабах, слишком мелких для тогдашних микроскопов и вообще каких бы то ни было средств наблюдения, вещество выглядит совсем не так, как считалось прежде. Физики и химики начали принимать всерьез странную теорию, возникшую более 2000 лет назад и восходящую к философствованиям древнего грека Демокрита и индийских ученых. Идея заключалась в том, что, хотя мир, судя по всему, сделан из бесчисленного множества различных материалов, все вещество на самом деле построено из крохотных частичек — атомов. Слово «атом» по-гречески означает «неделимый».

Химики XIX в. нашли немало косвенных свидетельств существования атомов: элементы, соединяясь вместе и образуя более сложные молекулы, делают это в очень конкретных соотношениях, часто близких к целым числам. Джон Дальтон сформулировал свои наблюдения в виде закона кратных пропорций и предложил в качестве объяснения атомы. Если каждое химическое соединение состоит из фиксированного числа атомов разных видов, то такое соотношение появится автоматически. К примеру, нам сегодня известно, что каждая молекула двуокиси углерода состоит из двух атомов кислорода и одного атома углерода, так что атомы в этом веществе всегда будут присутствовать в отношении два к одному. Однако есть и сложности: разные атомы имеют разную массу, а многие элементы существуют в виде молекул, состоящих из нескольких атомов — к примеру, молекула кислорода состоит из двух атомов кислорода. И если вы не понимаете, что происходит, то решите, что атом кислорода вдвое массивнее, чем на самом деле. Кроме того, некоторые распространенные элементы на самом деле представляют собой смесь разных «изотопов» — атомных структур. К примеру, хлор существует в природе в виде смеси двух стабильных форм, известных как хлор-35 и хлор-37 в соотношении примерно 76 и 24 % соответственно. Так что наблюдаемый «атомный вес» хлора равен 35,45. Зарождающаяся атомная теория интерпретировала это как «атом хлора состоит из тридцати пяти с половиной атомов водорода». А это означало, что атом не является неделимым. Век XX уже начался, а большинство ученых по-прежнему считало, что принятие атомной теории — слишком решительный шаг, чтобы сделать его, основываясь на таких данных.

Некоторые ученые, в первую очередь Максвелл и Людвиг Больцман, продвинулись дальше других и были убеждены, что газы — это тонко распределенные наборы молекул и что молекулы получаются при соединении атомов. Большинство их коллег убедило, судя по всему, данное Эйнштейном объяснение броуновского движения — хаотичного движения крохотных частиц взвеси, видимых под микроскопом. Эйнштейн решил, что эти подергивания вызываются столкновениями с хаотично движущимися молекулами жидкости. Он также провел кое-какие численные расчеты, подтвердившие эту точку зрения. Жан Перрен в 1908 г. подтвердил эти предположения экспериментально. Возможность видеть действие предполагаемых неделимых частиц вещества и делать на основании увиденного численные предсказания оказалась для ученых гораздо более убедительной, чем философские рассуждения и занятная нумерология. В 1911 г. Амедео Авогадро разобрался в проблеме изотопов, и существование атомов было признано окончательно.

Пока все это происходило, кое-кто из ученых начал понимать, что атомы вовсе не являются неделимыми. Они обладают структурой, и от них можно отбивать маленькие кусочки. В 1897 г. Джозеф Томсон, экспериментируя с катодными лучами, открыл, что атомы можно заставить испускать еще более мелкие частицы, электроны. И не только это: оказалось, что атомы разных элементов испускают одни и те же частицы. При помощи магнитного поля Томсон показал, что электроны несут отрицательный электрический заряд. Но атом электрически нейтрален, так что в нем должна быть какая-то часть, обладающая положительным зарядом. Обдумав это, Томсон предложил модель атома, известную как «пудинг с изюмом»: атом похож на положительно заряженный пудинг с отрицательно заряженными электронами-изюминками внутри. Но в 1909 г. Эрнест Резерфорд, один из бывших студентов Томсона, провел эксперимент и продемонстрировал, что большая часть массы атома сосредоточена возле его центра. Пудинги такими не бывают.

Как можно экспериментально прозондировать такую крохотную область пространства? Представьте себе участок земли, на котором могут быть здания и другие сооружения, а может и не быть ничего. Вам не позволяется входить на эту территорию, к тому же вокруг темно, хоть глаз выколи, и ничего не видно. Однако у вас есть винтовка и неограниченный запас патронов. Вы можете стрелять наугад в направлении участка и отслеживать направление, в котором пули из него вылетают. Если участок напоминает пудинг с изюмом, то большая часть пуль пролетит насквозь по прямой. Если вам придется время от времени уворачиваться от пуль, срикошетивших прямо на вас, то можно будет сделать вывод, что впереди находится что-то довольно твердое. Наблюдая за тем, как часто пули вылетают с участка под тем или иным углом, вы сможете оценить размеры твердого объекта.

Пулями Резерфорда стали альфа-частицы — ядра атомов гелия, а участком земли для него служила тончайшая золотая фольга. Работа Томсона показала, что электроны-изюминки обладают очень малой массой, так что почти вся масса атома должна была приходиться на сам пудинг. Если бы в пудинге не было уплотнений, то бо́льшая часть альфа-частиц должна была бы пролетать насквозь. Лишь некоторые частицы могли отклоняться от своего пути, и то ненамного. Вместо этого оказалось, что небольшая, но заметная часть альфа-частиц отклонялась на достаточно большие углы, что явно не соответствовало картине пудинга. Резерфорд предложил другую метафору, которой мы часто пользуемся и сегодня, несмотря на существование более современных моделей. Речь идет о планетарной модели атома. Атом подобен Солнечной системе, предположил Резерфорд: в нем есть громадное центральное ядро, «солнце» системы, а вокруг ядра, подобно планетам, обращаются электроны. Поэтому атом, как и Солнечная система, по большей части представляет собой пустое пространство.

Резерфорд пошел дальше и нашел доказательства того, что ядро состоит из двух различных типов частиц: протонов, несущих положительный заряд, и нейтронов с нулевым зарядом. Массы тех и других очень близки и примерно в 1800 раз превосходят массу электрона. Таким образом, атомы не только не являются неделимыми, но и состоят из еще более мелких субатомных частиц. Эта теория объясняет целочисленную нумерологию химических элементов: оказывается, подсчитывается не что-нибудь, а количество протонов и нейтронов. Кроме того, она объясняет изотопы: добавление или удаление нескольких нейтронов изменяет массу атома, но сохраняет его суммарный нулевой заряд и число электронов, равное числу протонов. Химические свойства атома определяются в основном его электронами. К примеру, хлор-35 содержит 17 протонов, 17 электронов и 18 нейтронов; хлор-37 − 17 протонов, 17 электронов и 20 нейтронов. Атомная масса 35,45 возникает потому, что природный хлор представляет собой неравную смесь этих двух изотопов.

В начале XX в. появилась и новая теория, применимая к веществу в масштабе субатомных частиц. Она получила название «квантовая механика», и после ее появления физика принципиально изменилась и уже никогда не будет прежней. Квантовая механика предсказала множество новых явлений, которые затем удалось пронаблюдать в лаборатории, и существование новых элементарных частиц. Она также помогла понять прежде не поддававшиеся объяснению явления. Наконец, она изменила наши представления о Вселенной, поскольку классический ее образ, несмотря на великолепную согласованность со всеми предыдущими наблюдениями, оказался неверен. Человеческие органы чувств плохо приспособлены для восприятия реальности на фундаментальном уровне.

В классической физике вещество состоит из частиц, а свет представляет собой волну. В квантовой механике свет тоже частица, фотон; и наоборот, вещество (к примеру, электроны) может иногда вести себя как волна. Прежнее четкое деление на волны и частицы не то чтобы размывается, а вовсе исчезает, сменяясь корпускулярно-волновым дуализмом. Если воспринимать все буквально, планетарная модель атома работала не слишком хорошо, поэтому вскоре появился новый образ. Электроны не обращаются вокруг ядра, как планеты вокруг Солнца, а образуют размытое облако с центром в ядре — облако вероятностей, а не чего-то конкретного. Плотность облака в некоторой точке соответствует вероятности обнаружить в данной точке электрон.

Итак, помимо протонов, нейтронов и электронов физики знали еще одну субатомную частицу — фотон. Вскоре появились и другие. Кажущееся нарушение закона сохранения энергии побудило Вольфганга Паули предложить коллегам исправить положение — постулировать существование нейтрино, невидимой и практически необнаружимой новой частицы, которая объяснила бы утечку энергии. Необнаружимость частицы, однако, оказалась неполной, что позволило в 1956 г. подтвердить ее существование. После этого как будто распахнулись шлюзы. Пионы, мюоны, каоны посыпались как из рога изобилия (последние были открыты в результате наблюдения космических лучей). Появилась новая дисциплина — физика элементарных частиц, и первым ее рабочим инструментом стал метод Резерфорда, позволявший проводить зондирование на тех невероятно малых масштабах, о которых шла речь: чтобы выяснить, как устроен тот или иной объект, нужно бомбардировать его разными «снарядами» и смотреть на результат. Началось строительство и использование все более масштабных ускорителей частиц — по существу, орудий, стреляющих теми самыми пробными снарядами. Стэнфордский линейный ускоритель имел длину 3 км. Чтобы не строить ускорителей длиной в целый континент, их стали изгибать и замыкать в круг, чтобы частицы могли беспрерывно двигаться по ним, одновременно набирая колоссальные скорости. Это серьезно усложнило технологию, поскольку частицы при движении по кругу излучают энергию, но с этим научились справляться.

Первым результатом этих трудов стал растущий каталог элементарных вроде бы частиц. Энрико Ферми так выразил свое разочарование: «Если бы я мог запомнить названия всех этих частиц, я был бы ботаником». Однако время от времени в квантовой теории появлялись новые идеи, и список вновь менялся: предлагались очередные мельчайшие частицы, чтобы объединить уже наблюдавшиеся структуры.

Вначале квантовая механика описывала отдельные волноподобные или частицеподобные явления, но никто не мог вразумительно описать квантово-механический аналог поля. Однако игнорировать этот пробел было невозможно, потому что частицы, описываемые квантовой механикой, могут взаимодействовать и взаимодействуют с полями, которые на тот момент квантовой механикой не описывались. Представьте, что кто-то захотел бы выяснить, как движутся планеты Солнечной системы, притом что ньютоновы законы движения (описывающие, как движутся массы под действием сил) были бы известны, а вот его же закон тяготения (объясняющий, что представляют собой эти силы) — нет.

Но помимо частиц была и другая причина стремиться прояснить вопрос с полями. Благодаря корпускулярно-волновому дуализму то и другое теснейшим образом связано. По существу, частица — это скомканный кусочек поля, а поле — это море плотно упакованных частиц. Эти две концепции неразделимы. К несчастью, разработанные к тому моменту методы были основаны на том, что частицы похожи на крохотные точки, и никак не распространялись на поля. Невозможно просто согнать множество частиц в одно место и назвать то, что получилось, полем, потому что частицы взаимодействуют друг с другом.

Представьте толпу людей… к примеру, в поле. Может быть, они собрались там послушать рок-концерт. Если посмотреть из пролетающего вертолета, толпа людей похожа на жидкость, хлюпающую в поле — часто буквально, как, к примеру, на фестивале в Гластонбери: известно, что поле там превращается в море грязи. Внизу, на земле, становится ясно, что на самом деле жидкость — это бурлящая масса отдельных частиц: людей. Или, возможно, тесных небольших групп людей, таких как несколько гуляющих вместе друзей, которые представляют собой неделимую единицу, или как группа незнакомых людей, объединенных общей целью — к примеру, походом в бар. Но невозможно точно смоделировать толпу, просто сложив воедино поведение отдельных людей (то, как они вели бы себя в одиночестве). Направляясь к бару, одна группа преграждает путь другой, группы сталкиваются и перемешиваются. Разработка эффективной квантовой теории поля напоминает моделирование поведения толпы, в которой роль людей выполняют локализованные квантовые волновые функции.

К концу 1920-х гг. физики убедились (в частности, при помощи подобных рассуждений), что, как бы трудна ни была задача, квантовую механику придется расширять, чтобы она могла описывать не только частицы, но и поля. Естественной отправной точкой для этого стало электромагнитное поле. Необходимо было каким-то образом квантовать и электрический, и магнитный его компоненты, т. е. переписать его характеристики на языке квантовой механики. Но тут возникали сложности. Математический аппарат квантовой механики был незнаком и к тому же выглядел крайне нефизически. То, что можно было увидеть и измерить, уже не выражалось добрыми старыми числами, а соответствовало операторам гильбертова пространства: математическим правилам, разработанным для работы с волнами. Эти операторы нарушали обычные постулаты классической механики. При перемножении двух чисел результат не зависит от их порядка; к примеру, 2 × 3 и 3 × 2 — это одно и то же. Это свойство сложения, известное как коммутативность, нарушается для многих пар операторов — примерно так же, как надеть сначала носки, а затем ботинки, не то же самое, что сначала надеть ботинки, а затем носки. Числа — существа пассивные, а вот операторы — активны. Действие, которое вы произведете первым, подготавливает сцену для дальнейших событий.

Коммутативность — очень приятное математическое свойство. Его отсутствие раздражает и мешает, поэтому, в частности, квантование поля оказалось такой хитрой задачей. Тем не менее она решаема. Электромагнитное поле удалось квантовать в несколько этапов. Начался этот процесс с теории электрона Дирака (1928 г.), а завершили его Синъитиро Томонага, Джулиан Швингер, Ричард Фейнман и Фримен Дайсон в конце 1940-х — начале 1950-х гг. Получившаяся в результате теория стала называться квантовой электродинамикой.

Точка зрения, использованная при разработке этой теории, давала подходы к методу, который мог бы применяться и более широко. В основе его лежала идея, восходившая непосредственно к Ньютону. Пытаясь решить уравнения, связанные с законом Ньютона, ученые открыли несколько полезных общих принципов, известных как законы сохранения. Дело в том, что при движении системы массивных тел некоторые величины остаются неизменными. Самая известная из них — энергия, которая бывает двух видов: кинетическая и потенциальная. Кинетическая энергия определяется тем, насколько быстро движется тело, а потенциальная — представляет собой работу, проделанную определенными силами. Когда камень падает со скалы, он как бы обменивает потенциальную энергию, связанную с тяготением, на кинетическую. Говоря обычным языком, он падает и ускоряется. Кроме этого, сохраняются такие величины, как импульс, равный произведению массы на скорость, и момент импульса, связанный со скоростью вращения тела. Сохраняющиеся величины связывают различные переменные, используемые для описания системы, и таким образом уменьшают их число. Это очень полезно при решении уравнений, как мы уже видели в главе 8, где речь шла о задаче двух тел.

К началу XX в. ученые разобрались в том, откуда взялись законы сохранения. Эмми Нетер доказала, что каждая сохраняющаяся величина соответствует непрерывной группе симметрий в уравнениях. Симметрия — это математическое преобразование, при котором уравнения не меняются. Все симметрии образуют группу с операцией «провести одно преобразование, затем другое». Непрерывная группа — это группа симметрий, определенная единственным действительным числом. К примеру, вращение вокруг заданной оси есть симметрия, и угол вращения может задаваться любым действительным числом, поэтому вращения — на все возможные углы — вокруг заданной оси образуют непрерывную группу. Из сохраняющихся величин с этой симметрией связан момент импульса, или вращательный момент. Точно так же сохранение импульса связано с непрерывной группой перемещений в заданном направлении. А как насчет энергии? Ее сохранение связанно с временны́ми симметриями — уравнения неизменны в любой момент времени.

Попытавшись унифицировать фундаментальные силы природы, физики убедились, что ключ к единой теории — именно симметрии. Первым такая унификация удалась Максвеллу, который соединил электричество и магнетизм в единое электромагнитное поле. Максвелл сделал это без привлечения симметрии, но вскоре стало ясно, что в его уравнениях присутствует особый вид симметрии, которого прежде никто не замечал: калибровочная симметрия. Создавалось впечатление, что она может стать стратегическим рычагом, при помощи которого ученым удастся открыть путь к более общим квантовым теориям поля.

Вращение и перенос — глобальные симметрии: они равно применимы в любой точке пространства и времени. Вращение вокруг определенной оси поворачивает на один и тот же угол каждую точку пространства. Не таковы калибровочные симметрии: это местные симметрии, они могут меняться от одной точки пространства к другой. В случае электромагнетизма местные симметрии — это смена фазы. Колебания электромагнитного поля в определенной точке обладают амплитудой (это размах колебаний) и фазой (это момент, в который колеблющаяся величина достигает своего максимума). Если взять решение уравнений поля Максвелла и в каждой точке поменять фазу, то получится другое решение (если, конечно, вы внесете в описание поля соответствующее компенсирующее изменение, включающее местный электромагнитный заряд).

Калибровочные симметрии ввел в обращение Герман Вейль в безуспешной попытке добиться дальнейшей унификации электромагнетизма и общей теории относительности, т. е. электромагнитных и гравитационных сил. Название появилось в результате недопонимания: он считал, что правильная местная симметрия должна означать изменение пространственного масштаба, т. е. «калибровку». Из этой идеи ничего не получилось, но логика квантовой механики заставила Владимира Фока и Фрица Лондона предложить другой тип местной симметрии. Квантовая механика формулируется с использованием не только действительных, но и комплексных чисел, и каждая квантовая волновая функция имеет комплексную фазу. Значимые местные симметрии вращают фазу на любой угол на комплексной плоскости. В принципе, эта группа симметрий включает в себя все вращения, но в комплексных координатах все они представляют собой «унитарные трансформации» (U) в пространстве с одним комплексным измерением (1), поэтому группа, сформированная этими симметриями, обозначается как U(1). Формальные обозначения здесь не просто математическая игра: они позволили физикам записать, а затем и решить уравнения для заряженных квантовых частиц, движущихся в электромагнитном поле. Именно благодаря этому Томонага, Швингер, Фейнман и Дайсон разработали первую релятивистскую квантовополевую теорию электромагнитных взаимодействий: квантовую электродинамику. Симметрия калибровочной группы U(1) играла в их работах фундаментальную роль.

Следующий шаг, объединивший квантовую электродинамику с теорией слабого ядерного взаимодействия, сделали в 1960-е гг. Абдус Салам, Шелдон Глэшоу, Стивен Вайнберг и другие ученые. К электромагнитному полю с его калибровочной симметрией U(1) они добавили поля, связанные с четырьмя элементарными частицами — так называемыми бозонами W⁺, W⁰, W^— и B⁰. Калибровочные симметрии такого поля, по существу, вращают комбинации этих частиц, порождая другие их комбинации; эти симметрии образуют другую группу, получившую обозначение U(2) — унитарные (U) трансформации в двумерном комплексном пространстве (2), являющиеся также специальными (S) — простое формальное условие. Иными словами, полная калибровочная группа — это U(1) × SU(2), где знак × указывает на то, что две группы действуют независимо на двух разных полях. Результат, получивший название теории электрослабых взаимодействий, потребовал введения сложного математического новшества. Группа U(1) в квантовой электродинамике коммутативна: два проведенных последовательно симметричных преобразования дают один и тот же результат, в каком бы порядке они ни проводились. Это свойство сильно упрощает всю математику, но для группы SU(2) не работает. Так впервые была применена некоммутативная калибровочная теория.

Сильное ядерное взаимодействие вступает в игру при рассмотрении внутренней структуры таких частиц, как протоны и нейтроны. Толчком к большому прорыву в этой области послужила интересная математическая закономерность, наблюдаемая в одном конкретном классе частиц, известных как адроны. Эта закономерность, известная как «восьмеричный путь», вдохновила ученых на создание теории квантовой хромодинамики. Теория постулировала существование скрытых частиц, названных кварками, и использовала их в качестве базовых компонент для целого зоопарка адронов.

Согласно Стандартной модели, все во Вселенной состоит из 16 по-настоящему элементарных частиц, существование которых подтверждено экспериментами на ускорителях. Плюс 17-я частица, поисками которой в настоящее время занят Большой адронный коллайдер. Из частиц, известных еще Резерфорду, ранг элементарных сохранили только две: электрон и фотон. Протон и нейтрон, напротив, состоят из кварков. Это название пустил в оборот Марри Гелл-Ман, позаимствовав его из романа Джеймса Джойса «Поминки по Финнегану». Гелл-Ман хотел, чтобы слово quark произносилось как «корк», однако фраза из романа Джойса, в которой оно встречается: «Три кварка для мастера Марка!» — подразумевает, что слово quark должно рифмоваться с именем Марк. Тем не менее Гелл-Ман нашел способ обосновать свое намерение. Сегодня в английском языке распространены оба варианта произношения.

В Стандартной модели предполагается существование шести кварков, объединенных попарно. Названия кварков довольно забавны: верхний/нижний, очарованный/странный, истинный/прелестный. Кроме того, модель предусматривает шесть лептонов, тоже парных: электрон, мюон и таон (который чаще называют по старинке тау-частицей) и соответствующие им нейтрино. Все эти 12 частиц называют фермионами — в честь Энрико Ферми. Частицы удерживаются вместе силами четырех типов: это гравитация, электромагнетизм, сильное и слабое ядерные взаимодействия. Оставив в стороне гравитацию, которую до сих пор не удалось полностью согласовать с квантовой картиной мира, получаем три силы. В физике элементарных частиц действие сил осуществляется посредством обмена частицами, которые их «переносят» или «передают». Традиционная аналогия — теннисисты, которых удерживает в пределах площадки их обоюдное внимание к мячу. Фотон переносит электромагнитное взаимодействие, Z— и W-бозоны переносят слабое ядерное взаимодействие, а посредством глюона передается сильное ядерное взаимодействие. Технически глюон переносит «цветное» взаимодействие, или взаимодействие между кварками, удерживающее их вместе, и, соответственно, сильное взаимодействие, которое мы наблюдаем в результате. Протон состоит из двух верхних кварков и одного нижнего; нейтрон — из двух нижних и одного верхнего. В каждой из этих частиц именно глюоны удерживают кварки на месте. Четыре перечисленных переносчика взаимодействий обобщенно называют бозонами, в честь Шатьендраната Бозе. Разница между фермионами и бозонами очень существенна: у них разные статистические свойства. На рис. 44 слева можно увидеть итоговый каталог предположительно элементарных частиц. На рис. 44 справа показано, как собрать протон и нейтрон из кварков.

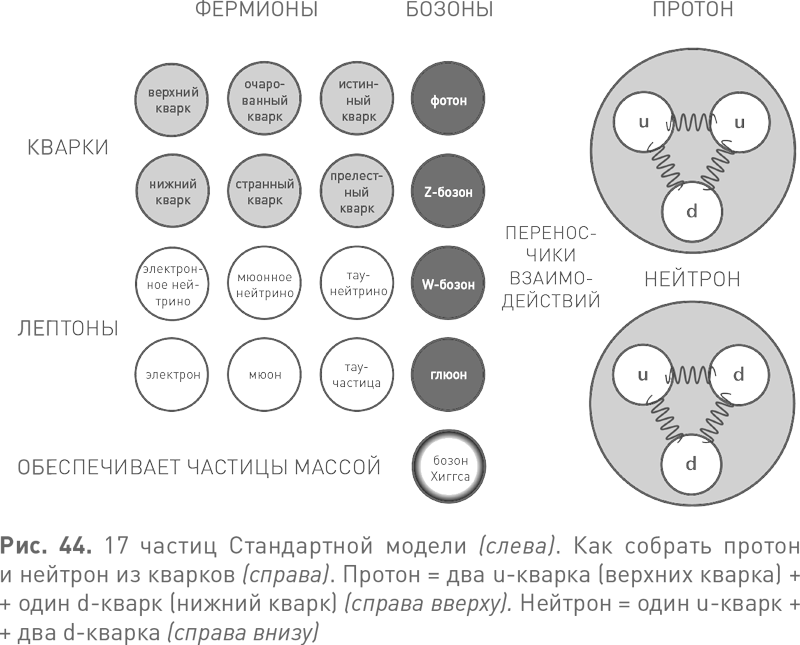
Бозон Хиггса завершает картину и объясняет, почему остальные 16 частиц Стандартной модели обладают ненулевыми массами. Он назван в честь Питера Хиггса — одного из тех физиков, которым принадлежала первоначальная идея. Кроме него, в работе над теорией, связанной с бозоном Хиггса, участвовали Филип Андерсон, Франсуа Энглер, Роберт Браут, Джеральд Гуральник, Карл Хаген и Томас Киббл. Бозон Хиггса — это воплощенное в частице гипотетическое квантовое поле — поле Хиггса — с необычным, но очень важным свойством: в вакууме оно не равно нулю. Это поле действует на остальные 16 частиц модели, заставляя их вести себя так, будто они обладают массой.

В 1993 г. Дэвид Миллер, отвечая на вызов британского министра науки Уильяма Уолдгрейва, предложил замечательную аналогию. Представьте себе многолюдную вечеринку. Гости равномерно распределены по залу, и тут входит почетный гость (отставной премьер-министр). Сразу же вокруг него собирается толпа народу. Гость движется по залу, кто-то из других гостей присоединяется к группе, кто-то отходит. Толпа сопровождающих придает почетному гостю дополнительную массу, ему теперь трудно остановиться. Это и есть механизм Хиггса. А теперь представьте, что по залу неожиданно разносится какой-то слух, и люди собираются послушать новости. Эта группа — бозон Хиггса. Миллер тогда добавил: «Может оказаться, что механизм Хиггса и поле Хиггса пронизывают всю Вселенную, а бозона Хиггса не существует. Следующее поколение коллайдеров прояснит этот вопрос». Судя по всему, вопрос с бозоном Хиггса действительно прояснился, а вот поле Хиггса требует дополнительных исследований.

Квантовая хромодинамика — это еще одна калибровочная теория, на этот раз с калибровочной группой SU(3). Как можно понять из обозначения, на этот раз преобразование действует на трехмерном комплексном пространстве. Из этого выводится унификация электромагнетизма, слабого и сильного взаимодействий. Предполагается, что существует три квантовых поля, по одному на каждое взаимодействие, с калибровочными группами U(1), SU(2) и SU(3) соответственно. Комбинация всех трех полей дает Стандартную модель с калибровочной группой U(1) × SU(2) × SU(3). Строго говоря, симметрии SU(2) и SU(3) приблизительны; считается, что они становятся точными при очень высоких энергиях. Поэтому их действие на частицы, составляющие ткань нашего мира, соответствует нарушенным симметриям — следам структуры, которые сохраняются в идеальной, полностью симметричной системе, подвергнувшейся небольшим возмущениям.

Все три группы содержат непрерывные семейства симметрий: одно семейство U(1), три — SU(2) и восемь — SU(3). Со всеми ними связаны различные сохраняющиеся величины. Симметрии ньютоновой механики, как обычно, обеспечивают сохранение энергии, импульса и момента импульса. Калибровочные симметрии U(1) × SU(2) × SU(3) свидетельствуют о сохранении различных «квантовых чисел», характеризующих частицы. Квантовые числа аналогичны таким величинам, как спин и заряд, но в отношении к кваркам. Здесь можно услышать такие названия, как цветовой заряд, изоспин или гиперзаряд. Наконец, в связи с U(1) сохраняются еще кое-какие величины: речь идет о квантовых числах шести лептонов, таких как электронное число, мюонное число и тау-число. В результате всего этого получается, что симметрии уравнений Стандартной модели объясняют через теорему Нетер все существенные физические переменные элементарных частиц.

Для нашей истории важны общая стратегия и результат. Чтобы унифицировать физические теории, нужно отыскать и унифицировать их симметрии. Затем нужно придумать подходящую теорию, в которой фигурировала бы объединенная группа симметрий. Я не говорю, что это простой и прямолинейный процесс, — технически это очень сложно. Но до сих пор квантовая теория поля развивалась именно так, и только одно из четырех фундаментальных физических взаимодействий — гравитация — пока выпадает из общей картины.

Теорема Нетер не только объясняет основные физические переменные, связанные с элементарными частицами, — именно так были открыты многие базовые симметрии. Исходя из квантовых чисел, которые удалось установить путем наблюдений или логических рассуждений, физики пытались выяснить, какими симметриями в этом случае должна обладать модель. Затем они составляли подходящие уравнения с этими симметриями и убеждались, что эти уравнения достаточно точно отражают реальность. В данный момент последний этап требует подбора величин 19 параметров — чисел, которые необходимо подставить в уравнения для получения количественных результатов. Девять из девятнадцати — это массы конкретных частиц: всех шести кварков, а также электрона, мюона и тау-частицы. Остальные параметры более технические: например, углы смешивания и фазовые связи. Семнадцать параметров известны из экспериментов, но два — все еще нет: они описывают до сих пор гипотетическое поле Хиггса. Однако сегодня есть все шансы измерить их, поскольку физики знают, где их искать.

Уравнения, которые используются в этих теориях, относятся к общему классу калибровочных теорий поля, известных как теория Янга — Миллса. В 1954 г. Янг Чжэньнин и Роберт Миллс попытались разработать калибровочные теории для объяснения сильного взаимодействия и связанных с ним частиц. Первые попытки закончились неудачей: после квантования поля выяснилось, что массы частиц при этом должны быть нулевыми. В 1960 г. Джеффри Голдстоун, Ёитиро Намбу и Джованни Йона-Лазинио нашли способ обойти эту проблему: они начали с теории, предсказывавшей безмассовые частицы, но затем модифицировали ее, постулировав нарушение некоторых симметрий. Иными словами, слегка изменили уравнения, введя в них новые асимметричные условия. Когда при помощи той же идеи модифицировали теорию Янга — Миллса, то получившиеся уравнения очень хорошо легли и в электромагнитную теорию, и в квантовую хромодинамику.

Янг и Миллс предположили, что калибровочная группа является специальной унитарной группой. К частицам применимы группы SU(2) и SU(3), специальные унитарные группы для двух или трех комплексных измерений, но вообще-то этот математический аппарат работает для любого числа измерений. Их теория в лоб атакует сложную, но неизбежную математическую проблему. В одном отношении электромагнитное поле отличается обманчивой простотой: его калибровочные симметрии коммутативны. В отличие от большинства квантовых операторов фазы можно менять в любом порядке. Но физики-то работали с квантовой теорией поля для субатомных частиц. Там калибровочная группа не коммутативна, что очень затрудняет квантование уравнений.

Добиться успеха Янгу и Миллсу помогло схематическое представление взаимодействий частиц, предложенное Ричардом Фейнманом. Любое квантовое состояние может быть представлено как суперпозиция бесчисленных взаимодействий частиц. К примеру, даже в вакууме есть пары частиц и античастиц, которые на мгновение возникают из небытия и тут же исчезают вновь. Простое столкновение двух частиц порождает умопомрачительный танец, в котором промежуточные частицы появляются и исчезают, мечутся взад и вперед, расщепляются и сливаются. Спасает лишь сочетание двух подходов. Уравнения поля для каждой конкретной фейнмановской диаграммы можно проквантовать, а затем сложить все отдельные вклады и представить себе полный эффект взаимодействия. Более того, самые сложные диаграммы встречаются редко и потому их вклад в общую сумму невелик. Тем не менее здесь есть серьезная проблема. Сумма, если рассматривать ее буквально, бесконечна. Янг и Миллс нашли способ перенормировать расчет таким образом, чтобы исключить бесконечное число слагаемых, которые, по идее, не должны много значить. Осталась конечная сумма, и ее величина очень точно соответствовала реальности. При первом знакомстве эта методика казалась почти непостижимой, но сегодня в ней многое прояснилось.

В 1970-е гг. к делу подключились математики. Майкл Атья обобщил теорию Янга — Миллса на большой класс калибровочных групп. Математика и физика начали подпитываться друг от друга. Работа Эдварда Уиттена и Натана Зайберга над топологическими квантовыми теориями поля породила концепцию суперсимметрии, в которой каждая известная частица имеет «суперсимметричного» партнера: электрону соответствует селектрон, кваркам — скварки. Это предположение упростило математику и позволило сделать кое-какие физические предсказания. Однако никому еще не удалось наблюдать хотя бы одну из этих новых частиц, а некоторые из них, вероятно, уже должны были появиться в экспериментах на Большом адронном коллайдере. В математической ценности этих идей никто не сомневается, а вот их непосредственное значение в физике пока под вопросом. Тем не менее они помогли многое прояснить в теории Янга — Миллса.

Квантовая теория поля — один из наиболее динамично развивающихся передовых рубежей математической физики, поэтому Институт Клэя захотел включить в группу задач тысячелетия что-нибудь из этой области. Выбрали проблему массовой щели. Речь в ней идет о важном математическом вопросе из физики элементарных частиц. Применение полей типа Янга — Миллса для описания элементарных частиц в терминах сильного ядерного взаимодействия сильно зависит от особого квантового свойства, известного как массовая щель. В теории относительности частица, летящая со скоростью света, приобретает бесконечную массу, если только ее масса покоя не равна нулю. Щель в спектре масс позволяет квантовым частицам иметь конечную ненулевую массу, несмотря на то что связанные с ними классические волны движутся со скоростью света. Если массовая щель существует, то любое состояние, не являющееся вакуумом, обладает энергией, превышающей энергию вакуума по крайней мере на некоторую фиксированную величину. Иными словами, существует ненулевой нижний предел массы частицы.

Эксперименты подтверждают существование массовой щели, и компьютерное моделирование уравнений тоже говорит в пользу этой гипотезы. Однако мы не можем считать, что модель соответствует реальности, а затем использовать данные экспериментов (т. е. реальность) для проверки математических свойств модели, потому что в этом случае логика зацикливается. Необходимо теоретическое доказательство. Ключевым шагом здесь стало бы строгое доказательство того, что квантовые версии теории Янга — Миллса существуют. В классическом (неквантовом) ее варианте ученые уже довольно хорошо разобрались, но квантовый аналог осложняется проблемой перенормировки — теми самыми бесконечностями, избавляться от которых приходится при помощи математических уловок.

Один многообещающий подход начинается с того, что непрерывное пространство превращают в дискретную пространственную решетку и записывают для решетки уравнение, аналогичное уравнению Янга — Миллса. Затем главное — показать, что по мере того, как решетка становится все мельче, постепенно приближаясь к сплошной среде, этот аналог сходится к четко определенному математическому объекту. На основании физической интуиции можно сделать вывод о некоторых необходимых его свойствах, и если бы эти свойства удалось установить строго, то можно было бы доказать и существование подходящей квантовой теории Янга — Миллса. Гипотеза о массовой щели требует более детальных представлений о том, как решетчатые теории аппроксимируют эту гипотетическую теорию Янга — Миллса. Так что существование этой теории и гипотеза массовой щели тесно взаимосвязаны.

На этом этапе все и застопорилось. В 2004 г. Майкл Дуглас составил отчет о состоянии проблемы, в котором написал: «Насколько мне известно, в последние годы в этом вопросе не было никаких прорывов. В частности, хотя в области теорий поля для низких размерностей достигнут некоторый прогресс, мне неизвестно, о каком бы то ни было существенном прогрессе в строительстве математически строгой квантовой теории Янга — Миллса». Судя по всему, это утверждение справедливо до сих пор.

В некоторых смежных задачах, однако, наблюдался более впечатляющий прогресс, и не исключено, что это поможет пролить свет и на интересующий нас вопрос. Частные случаи квантовой теории поля, известные как двумерные сигма-модели, разрешимы легче, и для одной такой модели гипотеза массовой щели уже доказана. Суперсимметричные квантовые теории поля, в которых фигурируют гипотетические суперпартнеры обычных элементарных частиц, отличаются некоторыми математическими свойствами, которые по существу, делают перенормировку ненужной. Физики, такие как Эдвард Уиттен, продвигаются к решению соответствующих задач в суперсимметричном случае. Можно надеяться, что некоторые из разработанных ими методик, возможно, подскажут новые пути решения первоначальной задачи. Но каковы бы ни были физические следствия и как бы ни разрешился в конце концов вопрос существования массовой щели, наработки, уже сделанные в этой области, безусловно, обогатили математику новыми важными понятиями и инструментами.