Когда стало понятно, что шифру подстановки присуща эта уязвимость, криптографы начали придумывать более изощренные способы кодирования, чтобы отразить атаки, использующие подсчет букв. Одна идея состояла в варьировании шифра подстановки. Вместо того чтобы использовать лишь один шифр подстановки для всего текста, вы можете поочередно использовать два различных шифра. Таким образом, если вы, к примеру, кодируете слово beef, то буквы е в нем будут закодированы по-разному, поскольку к первой из них применяется один шифр, а ко второй – другой. Может оказаться, что beef будет закодирована как PORK. Чем более безопасным вы желаете сделать ваше сообщение, тем больше различных шифров нужно использовать в нем.

Конечно, в криптографии требуется приходить к компромиссу между надежностью шифра и легкостью его использования. В самом надежном виде шифра, называемом одноразовым блокнотом, используется свой шифр подстановки для каждой из букв сообщения. Его почти невозможно взломать, потому что нет совершенно никакого намека, как браться за шифротекст. Этот вид шифра также неудобен и громоздок, ведь приходится использовать свой шифр подстановки для каждой из букв сообщения.

Французский дипломат XVI в. Блез де Виженер считал, что для воспрепятствования частотному анализу будет достаточно переключаться между несколькими шифрами подстановки. Хотя шифр Виженера, как он стал известен, на самом деле является значительно более надежной формой кодирования, его все же можно взломать. Британский математик Чарльз Бэббидж в конечном счете нашел метод, позволяющий сделать это. Бэббидж по праву считается дедушкой компьютерного века: он был убежден, что машины можно использовать для автоматических вычислений, а в лондонском Музее науки можно увидеть реконструкцию его «Разностной машины» – механического аппарата для проведения вычислений. Именно систематический подход к решению задач способствовал тому, что в 1854 г. у него появилась идея, как взломать шифр Виженера.

Метод Бэббиджа задействует важное математическое умение – распознавание закономерностей. Первое, что вам необходимо выяснить, – между сколькими различными шифрами подстановки происходит переключение. Поскольку слово the, как правило, многократно встречается в любом открытом тексте, нужно попытаться заметить повторы одной и той же трехбуквенной последовательности, это может послужить ключом к определению количества шифров подстановки. Например, вы замечаете частые повторы последовательности AWR, причем количество разделяющих символов между различными употреблениями AWR кратно четырем. Это будет хорошим указанием на то, что используется четыре шифра.

Как только у вас есть эта информация, вы можете разбить шифротекст на четыре группы. В первую группу входит первая буква, пятая буква, девятая буква и т. д. Во вторую группу включены вторая буква, шестая буква, десятая буква и т. д. Для каждой из этих четырех групп использовался один шифр подстановки. Так что вы можете применить частотный анализ поочередно к четырем группам и взломать шифр.

После взлома шифра Виженера начался поиск нового способа надежно кодировать сообщения. Когда в 1920-х гг. в Германии была разработана шифровальная машина «Энигма», многие сочли, что было создано совершенное кодирование, которое невозможно взломать.

Принцип работы машины «Энигма» основан на переключении на другой шифр замены всякий раз после кодирования буквы. Так, если бы я захотел зашифровать последовательность аааааа (вероятно, она могла бы означать, что у меня приступ боли), то каждая буква а была бы закодирована по-своему. Элегантность машины «Энигма» заключалась в том, что смена одного шифра другим происходила автоматически и крайне эффективно. Сообщение печаталось на клавиатуре. Над ней находился другой набор букв, называемый «ламповой панелью», загоравшаяся буква отображала то, как кодировалась вводимая буква. Электрическое соединение клавиатуры с ламповой панелью происходило не напрямую, а через три вращающихся диска (ротора), в каждом из которых содержался клубок проводов.

Можно понять принцип работы машины «Энигма», если представить большой цилиндр, составленный из трех вращающихся барабанов. На верхнем основании цилиндра вблизи края расположены 26 отверстий, помеченных буквами алфавита. Чтобы закодировать букву, вы роняете шар в отверстие, соответствующее данной букве. Шар падает в первый барабан, у которого 26 отверстий вдоль обода наверху и 26 отверстий вдоль обода внизу. Верхние и нижние отверстия соединены трубками, которые не ведут напрямую от верхних отверстий к нижним, а извиваются сложным образом. В результате шар, попадающий наверху в барабан, выйдет внизу совершенно в другом положении. Средний и нижний барабан устроены схожим образом, но трубки, соединяющие их верхние и нижние отверстия, проложены по-своему. Когда шар падает из отверстия на дне третьего барабана, он попадает в конечную часть устройства, где 26 отверстий опять-таки помечены буквами алфавита.

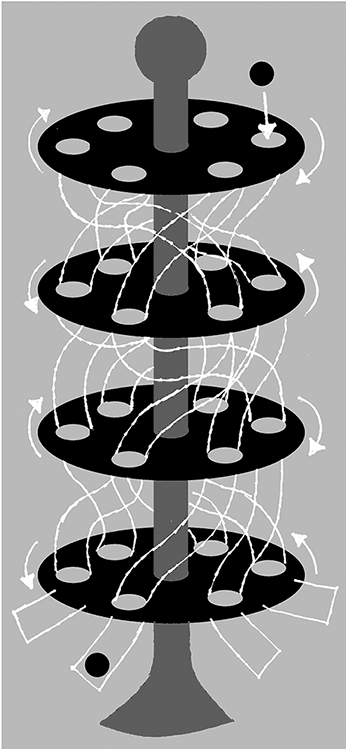
Рис. 4.02. Принцип работы шифровальной машины «Энигма»: опустите шар в отверстие наверху, соответствующее кодируемой букве. Барабаны вращаются после каждого кодирования, поэтому буквы всякий раз шифруются по-разному

Если бы устройство оставалось в таком же положении, то его действие сводилось бы к усложненному воспроизведению шифра подстановки. Но гениальность конструкции «Энигмы» состоит в том, что всякий раз, когда шар проходит через цилиндр, первый барабан поворачивается на 1/26 оборота. Поэтому, когда опускается следующий шар, первый барабан пошлет его совершенно по другому пути. Например, в первый раз буква а могла быть закодирована как С, но после того, как первый барабан повернулся на одну позицию, шар, брошенный в отверстие а, выйдет внизу в другом месте. Вот так и действовала машина «Энигма»: после кодирования первой буквы первый вращающийся диск поворачивался на одну позицию.

Вращение дисков в каком-то смысле соответствует одометру: после того как первый диск поворачивается на все 26 позиций и возвращается в начальное положение, он поворачивает второй диск на 1/26 оборота. Итак, имеется 26 × 26 × 26 различных способов шифровать буквы. Кроме того, оператор «Энигмы» мог менять порядок расположения дисков, что сводится к умножению количества возможных шифров подстановки на 6 (или 3! различных способов расположения трех дисков).

У каждого оператора была шифровальная книга, которая предписывала ему, в какое положение в начале того или иного дня нужно приводить три диска для кодирования сообщений. Получатель сообщения декодировал его, используя те же настройки из шифровальной книги. По мере усовершенствования «Энигмы» были введены дополнительные усложнения, что в конечном счете привело более чем к 158 миллионам миллионов миллионов различных способов установки машины.

В 1931 г. специалисты французской разведки сумели получить инструкцию по использованию шифровальной машины и пришли в ужас. Казалось, не существует никакой возможности понять из перехватываемого сообщения, в какое положение устанавливались диски для кодирования в тот день. А это было совершенно необходимо для дешифровки сообщения. Но у Франции было соглашение с Польшей по обмену разведывательной информацией, и угроза немецкого вторжения оказала стимулирующее воздействие на умственную деятельность поляков.

Польские математики поняли, что каждая из установок дисков характеризовалась своими особенностями в закодированных сообщениях, и этими закономерностями можно было воспользоваться для декодирования сообщений. Если, к примеру, оператор печатал а, то в зависимости от установки дисков эта буква кодировалась, скажем, как D. Затем первый диск поворачивался на одну позицию. Если оператор еще раз нажимал а и она кодировалась как Z, то в каком-то смысле связь D с Z определяется установкой дисков.

Мы могли бы исследовать это с помощью нашего приспособления. Устанавливая барабаны в требуемое положение и опуская по очереди в каждое из отверстий два шара, мы могли бы составить полный набор взаимосвязей, который мог бы выглядеть следующим образом (см. таблицу 4.03).

Каждая буква появляется в каждой строке один, и только один, раз, потому что каждая строка соответствует одному шифру подстановки.

Как поляки использовали эти взаимосвязи? В любой день все немецкие операторы «Энигмы» должны были использовать одну и ту же установку дисков, которая была записана в их шифровальной книге. Затем они выбирали свое собственное расположение дисков и посылали данные о нем, используя исходную установку дисков из шифровальной книги. Для надежности им было рекомендовано передавать сведения о выбранной установке дважды, что было, в противоположность надежности, фатальной ошибкой. Это давало полякам ключ к тому, какая установка дисков использовалась в машине «Энигма» в тот день.

Группа математиков, находившаяся в особняке Блетчли-парк, который расположен на полпути между Оксфордом и Кембриджем, изучала закономерности, подмеченные математиками в Польше, и нашла способ автоматизировать поиск настроек. При этом использовалась электронно-механическая машина под названием «Бомба». Говорят, что эти математики сократили Вторую мировую войну на два года и спасли бессчетное количество жизней. А построенные ими машины положили начало компьютерам, на которые мы полагаемся в наши дни.