Цепочка из почек
Почки выводят из организма балластные вещества. У большинства людей обе почки здоровы; если одна отказала, другая будет работать за двоих, позволяя человеку жить полноценной жизнью. Иногда отказывают обе почки, и тогда от смерти может спасти только регулярный диализ, который дорого стоит и отнимает много времени.
Если ваши почки здоровы, вы можете стать донором и отдать одну из них тому, у кого почки не функционируют вообще, – при условии совместимости с организмом реципиента. Совместимость проверяется с помощью несложного анализа крови.
Допустим, почки Элис вышли из строя. Ее муж, Боб, согласен стать донором. Если Боб пройдет тест на совместимость, врачи пересадят Элис его почку.
А если не пройдет? Тогда можно будет попытаться совершить обмен почками.
Предположим, Чарли требуется почка, его брат Дэвид готов отдать свою, но его почка не подходит. Если Дэвид совместим с Элис, а Боб – с Чарли, то можно провести операцию сразу на четырех пациентах, и в результате и Элис, и Чарли получат рабочую почку.
Представьте, что у нас имеется база данных с информацией по всем совместимым парам донор-реципиент. Тогда мы можем запустить на ней эффективный алгоритм, который найдет наибольшее возможное число обменов. Задача совсем не сложная и аналогична задаче о максимальном числе паросочетаний, рассмотренной в предыдущей главе.
Ограничиваться двумя парами за раз совсем не обязательно. В конце 2011 года силами шестидесяти хирургов была проведена цепочка из тридцати таких операций. Для тридцати человек это был единственный способ обрести здоровье.
Если мы в нашей базе разрешим обмен по цепочке, желая помочь как можно большему числу людей, то снова придем к NP-полной задаче. Равенство P и NP спасет чьи-то жизни, а это уже гораздо серьезнее, чем гарантированный выигрыш в игре «Сапер»!
Мастера конспирации
Как правило, те NP-задачи, которыми ученые занимались в середине семидесятых, довольно быстро либо оказывались NP-полными, либо «скатывались» в класс P, поскольку для них появлялись эффективные алгоритмы. Однако некоторые особо вредные экземпляры упорно не желали поддаваться классификации; одни сумели продержаться несколько лет, другие не удалось рассекретить до сих пор.
Изоморфизм графов
В Королевстве насчитывается несколько сотен фанатов «Блейд Квеста» – массовой многопользовательской ролевой онлайн-игры. Как и в других играх подобного плана, участники здесь получают новую личность, или аватар; каждый исполняет роль определенного персонажа и общается с другими персонажами, за которыми тоже стоят реальные жители Королевства. В виртуальном мире дружеские связи сохраняются: те, кто дружат в жизни, становятся друзьями и в игре, а те, кто враждуют, заново проникаются взаимной неприязнью.
Джон, Изабель, Кевин, Лаура, Молли и Нэнси очень любят играть в «Блейд Квест».
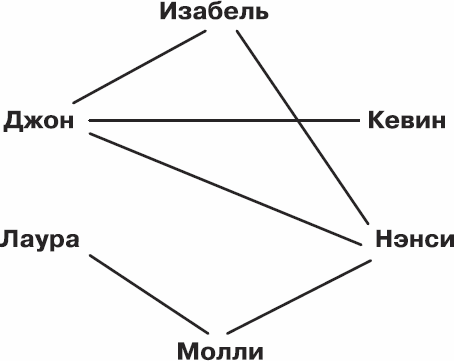
Рис. 4.10. Любители «Блейд Квеста»
Их персонажей зовут Акрис, Лэмбо, Криард, Де Гарольд, Хрхрхр и Вирус, но кто под каким именем скрывается – неизвестно: эта информация пользователям игры недоступна, и они могут видеть только схему дружеских связей между персонажами.
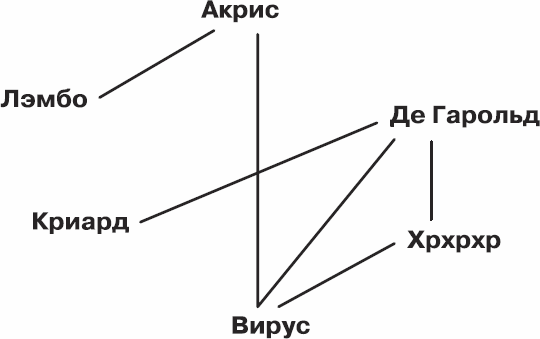
Рис. 4.11. Аватары в «Блейд Квесте»
Проанализировав обе схемы, Лаура отправила остальным игрокам сообщение от имени своего аватара: «Я знаю, кто ты!» А вы уже догадались, кто есть кто?
Схемы будут соответствовать друг другу лишь в том случае, если Изабель – это Хрхрхр, Джон – Де Гарольд, Кевин – Криард, Лаура – Лэмбо, Молли – Акрис, а Нэнси – Вирус. Например, «реальная» Молли дружит с Лаурой и Нэнси, а ее аватар Акрис – с Лэмбо и Вирусом.
Установить, соответствуют ли друг другу подобные схемы, – это все равно что определить, изоморфны два графа или нет. Некоторые схемы сопоставить нельзя, другие – можно, иногда даже несколькими способами. Проблема изоморфизма графов лежит в NP, поскольку, зная, кто есть кто, можно легко проверить соответствие дружеских связей.
Вопрос о том, относится ли проблема изоморфизма также и к классу P, до сих пор открыт; никто пока не придумал хороший алгоритм, который всегда находил бы искомое соответствие в случае, если оно действительно есть. Мы также не знаем, является ли эта проблема NP-полной, хотя, по мнению ученых, некоторые признаки косвенно указывают на то, что не является. Изоморфизм графов стоит в ряду немногочисленных задач, занимающих некое промежуточное положение: они вроде бы труднее, чем задачи из P, но легче, чем задачи NP-полные, вроде поиска гамильтонова пути или максимального разреза.
Простые числа. Разложение на множители
Число 15 можно разложить на множители, т. е. представить в виде произведения других натуральных чисел, двумя способами: 15 × 1 и 5 × 3. Для числа 24 способов уже гораздо больше, например – 24 × 1, 12 × 2, 8 × 3, 6 × 4. А вот число 17 иначе как в виде 17 × 1 не представишь: оно простое, т. е. делится только на себя и на единицу. Множество простых чисел бесконечно; первые восемь его представителей – 2, 3, 5, 7, 11, 13, 17, 19. Самое большое простое число, известное на момент написания этой книги, состоит из 12978189 цифр и начинается так: 316470269330255923143453723…
Как понять, является данное число простым или нет? К примеру, число 1123467619? Первое, что приходит в голову, – это методично перебрать все числа от 2 до 1123467618, пытаясь поделить на них исходное число. На самом деле достаточно будет дойти лишь до квадратного корня из 1123467619, т. е. перебрать все числа от 2 до 33518. Не такая уж и ужасная перспектива! А что, если взять число побольше? Например, такое:
8 273 820 869 309 776 799 973 961 823 304 474 636 656 020 157 784 206 028 082 108 433 763 964 611 304 313 040 029 095 633 352 319 623
Оно простое, как вы думаете?
Первые алгоритмы проверки на простоту придумали еще в Древней Греции, однако для больших чисел они не годились. В семидесятых годах прошлого века появились вероятностные алгоритмы, которые справлялись с числами из нескольких сот цифр. Проверка простоты осуществлялась при помощи серии тестов с использованием случайных чисел и некоторых методов теории чисел. Новые алгоритмы давали неплохие результаты, однако не гарантировали стопроцентную точность. Наконец, в 2002 году индийский профессор Маниндра Агравал вместе со своими студентами Нираджем Каялом и Нитином Саксеной создал точный и эффективный алгоритм распознавания простоты без использования случайных величин, доказав тем самым, что задача проверки числа на простоту лежит в классе P.
Алгоритм Агравала позволяет установить, что число 8 273 820 869 309 776 799 973 961 823 304 474 636 656 020 157 784 206 028 082 108 433 763 964 611 304 313 040 029 095 633 352 319 623
не является простым, но при этом не дает нам ни одного его делителя.
Удивительно, правда? Вопрос о простоте числа решается довольно быстро, а вот для поиска делителей эффективный алгоритм пока не придумали.
Задача разложения на множители принадлежит классу NP, поскольку при наличии готовых множителей их произведение можно посчитать очень легко. Например, умножив
84 578 657 802 148 566 360 817 045 728 307 604 764 590 139 606 051
на
97 823 979 291 139 750 018 446 800 724 120 182 602 777 022 032 973,
мы получим
8 273 820 869 309 776 799 973 961 823 304 474 636 656 020 157 784 206 028 082 108 433 763 964 611 304 313 040 029 095 633 352 319 623.
Маловероятно, что эта задача принадлежит классу P. Впрочем, в ее NP-полноту ученые тоже не верят: разложить число на множители, конечно, очень трудно, однако решить проблему выполнимости или раскраски карт, скорее всего, будет на порядок труднее.
Задачи распознавания простоты и поиска делителей важны не только для математиков, которые жить без своих чисел не могут. К примеру, практически неразложимые на множители числа используются в современной криптографии. В восьмой главе мы коснемся этой темы подробнее.

