Книга: Психология общих способностей
Назад: Атлас типичных рисунков Тест Торренса(завершение картинки)
Дальше: Диагностика вербальной креативности Адаптация теста С. Медника – подростковый и взрослый варианты{А. Н. Воронин, Т. В. Галкина}
Диагностика математического интеллекта Тест математических аналогий{ В. Н. Дружинин }
Задания, включаемые в тест математических аналогий, должны удовлетворять требованиям, предъявляемым к любым тестам способностей: быть стандартными, однородными по структуре, быть эквивалентными или же упорядоченными по трудности. Кроме того, они должны удовлетворять требованиям теоретической валидности: диагностировать математическую способность как таковую. К этому добавляется требование экологической валидности теста: соответствие его научно-практической задаче.
Поскольку важнейшим требованием, предъявляемым нами к задачам, была их применимость в школьной практике, в качестве тестового материала нами были использованы задачи, разработанные А. Г. Гайштутом, направленные на формирование у учащихся таких умственных операций, как анализ, синтез, аналогия, обобщение.
С точки зрения автора, «математика, как известно, наука доказательная или дедуктивная… Но доказательство открывается с помощью правдоподобного рассуждения, с помощью догадки. Два типа рассуждения – доказательное и правдоподобное – дополняют друг друга». Задачи, предложенные Гайштутом, сформулированы на основе материала из курса математики с 4-го по 10-й класс и состоят из 5 серий: 4-й класс, 5-й класс, 6-7-й классы, 8-й класс, 9-10-й классы. Решение задач каждого типа предполагает знание учебного материала, но, помимо того, способность к мысленному обнаружению отношений между пространственными и знаковыми элементами условий задачи и умение производить математические операции с математическими структурами. Таким образом, задачи, предложенные Гайштутом, могут быть использованы для диагностики уровня развития мышления, мыслительной способности оперировать абстрактными структурами на математическом материале.
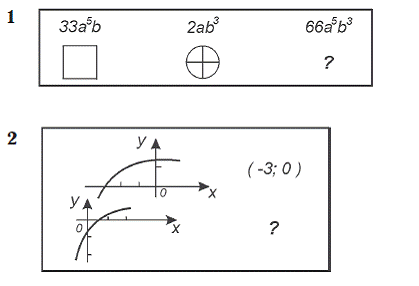
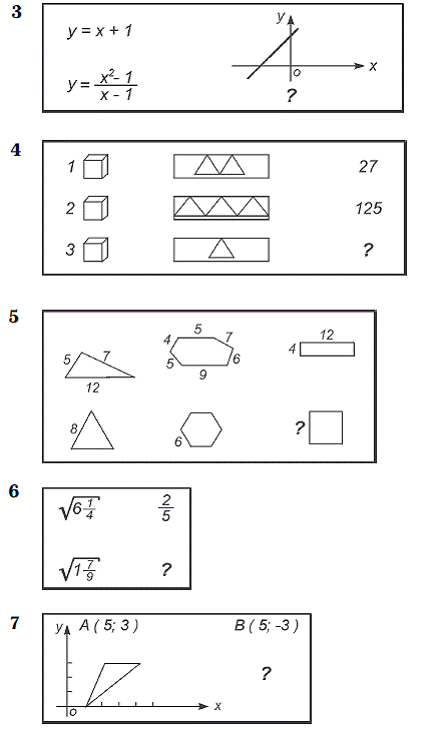
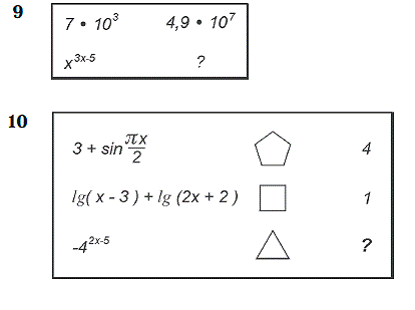
Рассмотрим образец задачи:
1. Найти Электричество XIII
Неизвестное математик?
В данные задачи входят 4 элемента, один из которых неизвестен. Требуется найти неизвестный элемент. Решение может быть найдено только тогда, когда будет решена вспомогательная задача: выделены отношения элементов начальных условий задачи. Между элементами «электричество» и XIII отношение тождества: число букв в слове «электричество» равно 13, между элементами «электричество» и «математик» – отношение различия: разное число букв. Следовательно, требуется, чтобы неизвестное находилось в отношении тождества с элементом «математик» и в том же отношении количественного различия с элементом XIII, как элементы «математик» и «электричество». Неизвестный элемент – число IX. Следовательно, испытуемый должен произвести операции сравнения элементов, выделить тип отношений – количественные различия и сделать умозаключение по аналогии. Как видно, отношения между элементами задачи арифметические, от испытуемого требуется знание цифровых обозначений и умение читать и считать, а также владение арифметическими действиями. Следовательно, данная задача соответствует уровню подготовки школьника 4-го класса. Тем самым, несмотря на то что в задаче присутствует конкретный материал и для его решения требуются стандартные знания и умения, успешно решить эту задачу можно, только обладая определенным уровнем развития мыслительной способности, оперируя с символическими (пространственно-знаковыми) структурами. Следовательно, задачи удовлетворяют выдвинутому нами требованию: диагностировать одновременно уровень развития продуктивного математического мышления (открытие новых отношений) и репродуктивного математического мышления (нахождение решения при помощи применения знаний). Поскольку материал теста должен соответствовать учебной программе средней школы, тест был разбит на 5 субтестов: 1) субтест для 4-го класса, 2) субтест для 5-го класса, 3) субтест для 6-го класса, 4) субтест для 7-8-го классов и 5) субтест для 9-10-го классов. 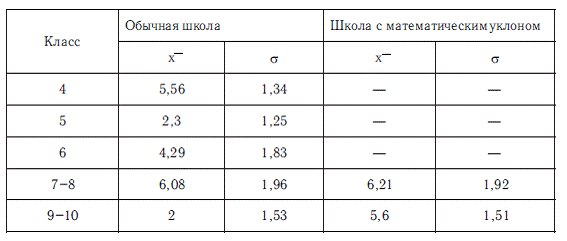
 Предлагаемый тест математических аналогий «Задачи Гайштута» (ТМА) может быть использован для диагностики уровня развития общего интеллекта и математических способностей. Тест обладает достаточной внутренней и внешней валидностью. Успешность выполнения теста связана с уровнем развития способности к мысленному решению задач, понятийного и пространственного мышления. Тест следует испытывать при проведении контрольных и самостоятельных работ, так как он стандартизирован в этих ситуациях. Следует избегать включения теста в экзаменационные работы. ТМА следует применять после прохождения соответствующего учебного материала, то есть в конце года (4, 5, 6-й классы) или 2-х лет обучения (7-8, 9-10-й классы). Задачи теста обладают высокой однородностью. Если испытуемые решат больше 5 заданий, можно считать, что они обладают высоким уровнем развития способности мыслить аналогиями. Если меньше, то не следует ставить определенный диагноз. Необходимо провести через некоторое время повторное обследование и использовать в качестве дополнения другие аналогичные тесты.
Предлагаемый тест математических аналогий «Задачи Гайштута» (ТМА) может быть использован для диагностики уровня развития общего интеллекта и математических способностей. Тест обладает достаточной внутренней и внешней валидностью. Успешность выполнения теста связана с уровнем развития способности к мысленному решению задач, понятийного и пространственного мышления. Тест следует испытывать при проведении контрольных и самостоятельных работ, так как он стандартизирован в этих ситуациях. Следует избегать включения теста в экзаменационные работы. ТМА следует применять после прохождения соответствующего учебного материала, то есть в конце года (4, 5, 6-й классы) или 2-х лет обучения (7-8, 9-10-й классы). Задачи теста обладают высокой однородностью. Если испытуемые решат больше 5 заданий, можно считать, что они обладают высоким уровнем развития способности мыслить аналогиями. Если меньше, то не следует ставить определенный диагноз. Необходимо провести через некоторое время повторное обследование и использовать в качестве дополнения другие аналогичные тесты.
Теперь приведем результаты стандартизации теста математических аналогий (ТМА).
Общее число испытуемых было равно 350. Число испытуемых каждого учебного класса – 50. Получены следующие значения средних и дисперсий, характеризующих трудность и дифференцирующую силу теста.

Выявилось, что субтесты для 5-го и для 9-го классов вызывали затруднения у учеников. Однако следует отметить, что тестирование учеников 9-10 классов обычной школы проходило после окончания уроков. Опрос учащихся показал, что они были утомлены и не испытывали интереса к выполнению заданий.
При тестировании в остальных классах получены значения х", близкие к 5 баллам (5 правильно решенных задач), что свидетельствует об эквивалентности заданий. Дисперсии среднего балла значимо не различаются. Следовательно, все субтесты обладают примерно равной дифференцирующей силой.
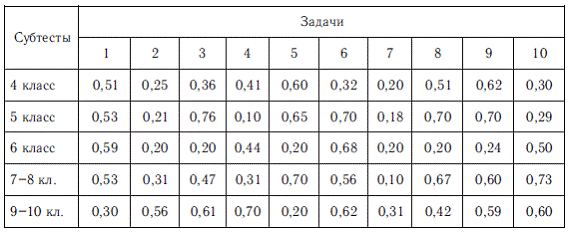
Рассмотрим показатели дифференцирующей силы и трудности отдельных заданий на примере субтеста для 7-8-го классов.
Коэффициент трудности отдельных заданий находится в пределах 0,25 < р <0,71.
Тем самым можно утверждать, что тестовые задания относятся к группе заданий средней трудности.
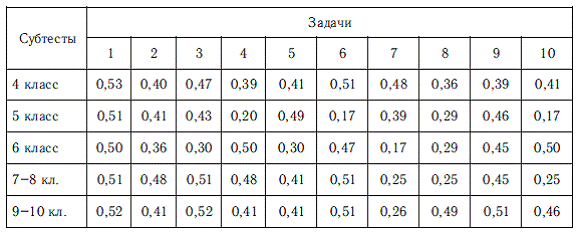
Приведем данные трудности задач для всех субтестов, где трудность равна отношению числа испытуемых, решивших тест, к общему числу испытуемых.

Соответствующие результаты оценки дифференцирующей силы задач в единицах стандартного отклонения (?).

Литература
1. Гайштут А. Г. Математика в логических упражнениях. Киев: Радянска школа, 1985. 192 с.
2. Гуревич К. М. Тесты интеллекта в психологии. // Вопросы психологии. 1982. № 2.С. 28-32.
3. Крутецкий В. А. Психология математических способностей. М.: Просвещение, 1968. 432 с.
4. Кулагин Б. В. Основы профессиональной психодиагностики. Л., 1984.
5. Мательский П. В. Психолого-педагогические основы дидактики математики. Минск: Вышейная школа, 1977. С. 149-160.
6. Пиаже Ж., Инельдер Б. Генезис элементарных логических структур: классификация и сериация. М.: Иностранная литература, 1963. 446 с.
7. Психодиагностика. Теория и практика / Под ред. Н. Ф. Талызиной. М.: Прогресс, 1986. 207 с.
8. Guilford J. Т. The ature of Human intelligence. N.Y.: McGraw-Hills, 1967. 538 p.
9. Witzlack G.Grundlagen der Psychodiagnostik. Berlin, 1977.Тест математических аналогий
4 класс 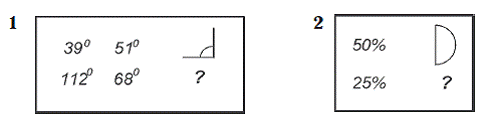
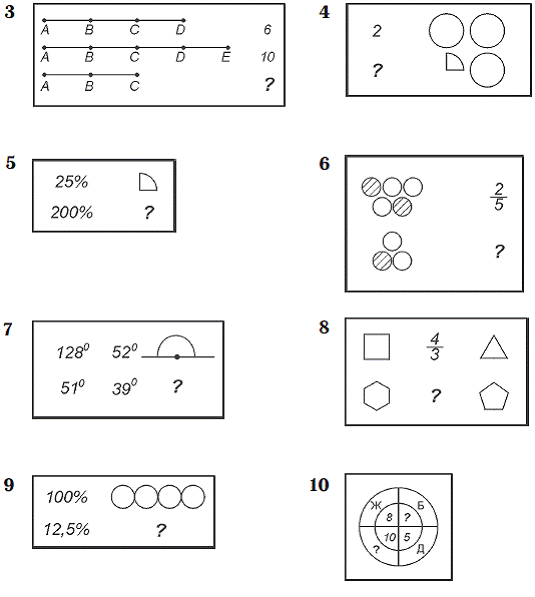
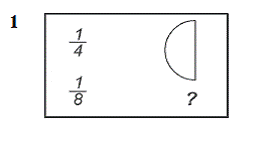
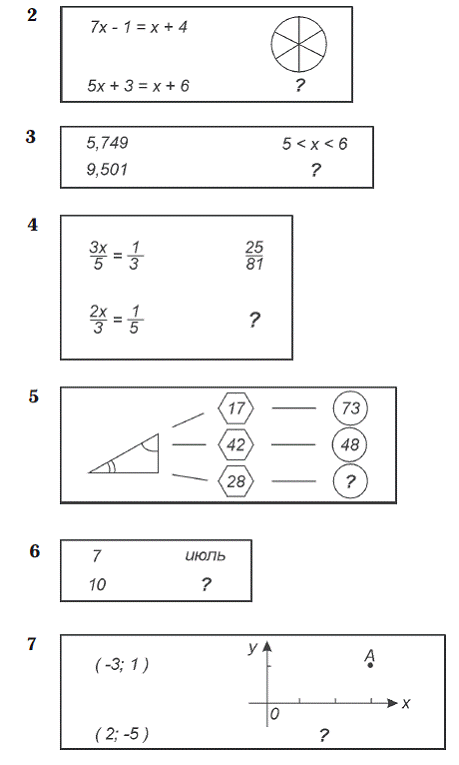
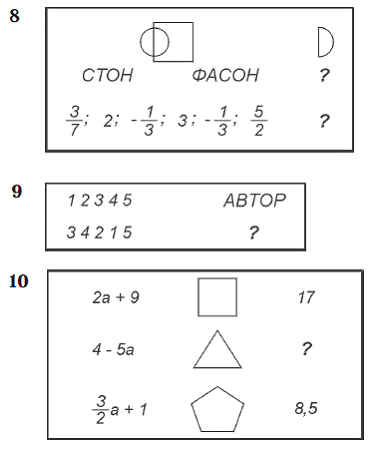
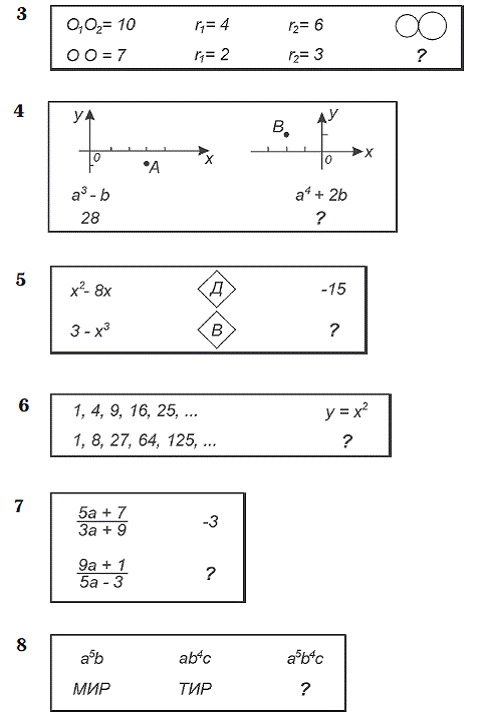
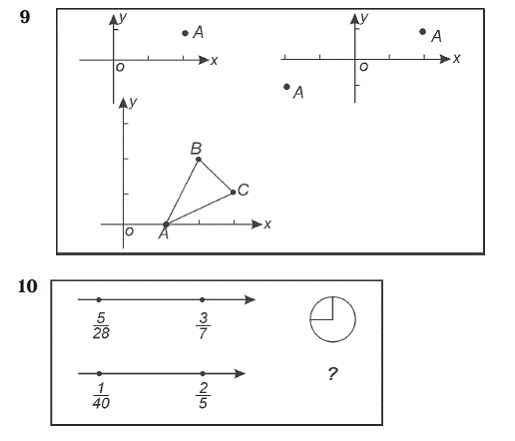
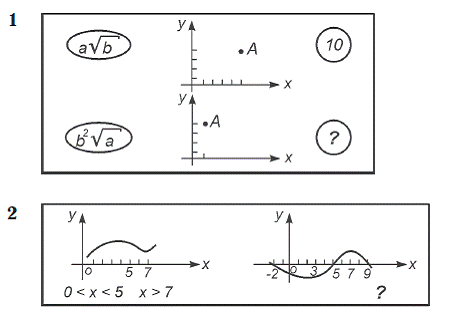
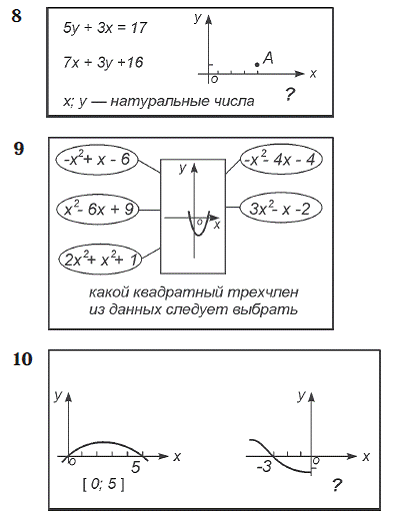
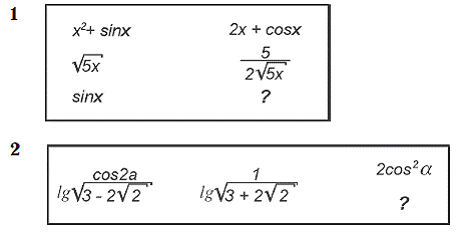
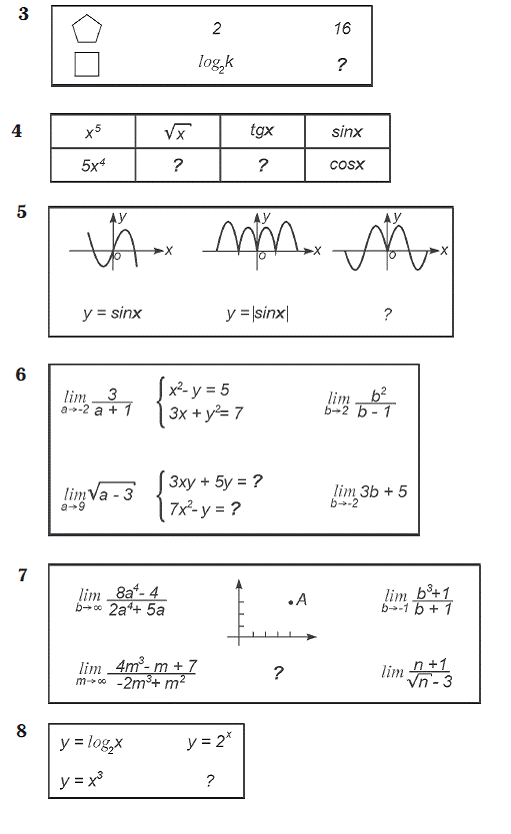
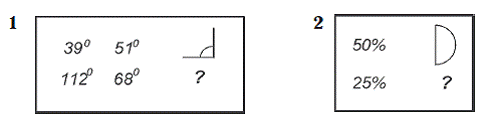

5 класс



6 класс



7-8 класс



9-10 класс



Назад: Атлас типичных рисунков Тест Торренса(завершение картинки)
Дальше: Диагностика вербальной креативности Адаптация теста С. Медника – подростковый и взрослый варианты{А. Н. Воронин, Т. В. Галкина}

