Глава 5. Музыка сфер
Математика во многих отношениях является самой сложной и утонченной наукой, по крайней мере мне как математику так кажется. Поэтому я нахожу особое удовольствие в том, что рассказываю о прогрессе в математике как части человеческого знания. Есть некоторые идеи, которые должен включать каждый рассказ о математике: логическая идея доказательства, эмпирическая идея о точности законов природы (и в частности пространства), возникновение понятия операций и переход от статического описания мира к динамическому. Этому и посвящена настоящая глава.
Начну с того, что даже у примитивных народов есть система исчисления. Конечно, они не всегда умеют считать дальше четырех, но они знают, что если к двум предметам прибавить два точно таких же, в сумме получается четыре, – и так будет всегда. С этого фундаментального правила начинается построение многих числовых систем, как правило, существующих в письменном виде и основанных на одних и тех же принципах. Вавилоняне, майя и народ Индии, например, независимо друг от друга изобрели по существу одинаковый способ записи больших чисел в виде последовательности цифр, который мы активно используем в современной жизни.
Таким образом, нет ни места, ни времени, про которые я мог бы определенно заявить: «Арифметика появилась здесь и сейчас». В каждой культуре люди начинали считать и говорить одновременно, поэтому арифметика, как и язык, началась в доисторическое время. Но математика в нашем понимании, оперирующая цифрами, – совершенно иное дело. И чтобы отыскать корни этой легенды, я отправляюсь в морской поход к острову Самос.
В доисторические времена Самос был центром поклонения Гере – Царице Небесной, законной (и очень ревнивой) супруге Зевса. Сохранившийся до наших дней храм Геры, называемый иногда Гераионом, датируется VI веком до н. э., построил его тиран Поликрат. На этом же острове в 580 году до н. э. родился первый гений человечества и основатель греческой математики Пифагор. Из-за разногласий с Поликритом он вынужден был покинуть остров, но, по легенде, долго скрывался от гнева правителя в горах. Доверчивым туристам сегодня с удовольствием показывают маленькую белую пещеру, в которой якобы жил Пифагор.
Самос – волшебный остров, его воздух исполнен морем, зеленью и музыкой. Для меня Самос – остров Просперо из шекспировской «Бури», берег, где ученый стал волшебником. Вероятнее всего, Пифагор казался волшебником своим последователям, поскольку учил, что природой управляют числа. Он говорил, что в природе есть гармония, в основе разнообразия лежит единство, и у него есть язык: числа – это язык природы.
Пифагор нашел основное соотношение между музыкальной гармонией и математикой. История этого дошла до нас только легендой, как народная сказка, но суть его остается точной. Звук, или основной тон, образует вибрация одной натянутой струны. Звуки, которые звучат гармонично с ним, получаются, если разделить струну на равное количество частей: точно на две части, точно на три части, точно на четыре части и т. д. Если точка, где вибрация меньше всего, не попадает на одну из этих точек, звук дисгармоничен.
Таким образом, сдвигая «точку невибрации» по струне, мы распознаем звуки, которые гармоничны. Итак, прижатая на середине струна дает нам обертон, который на октаву выше основного тона. Переместившись еще на 1/3 длины струны, поднимитесь на квинту выше, еще на 1/4 – на кварту и одновременно отдалитесь на две октавы от основного тона. Поднимитесь еще на 1/5 (правда, Пифагор этого сделать не предлагал) – получите звучание терции.
Пифагор доказал, что аккорды, которые звучат гармонично – для западного уха, – соответствуют точному делению струны на целые числа. Пифагорейцам открытие показалось настоящим колдовством: настолько было удивительным и убедительным согласие между природой и числами. На базе обертоновой структуры звука они вместе пришли к выводу, что все законы природы строятся на этом же принципе.
Например, чтобы вычислить орбиты небесных тел, которые, по их мнению, вращались вокруг Земли, надо связать их с музыкальными интервалами. Иначе говоря, греки утверждали, что все закономерности природы музыкальны, а движения небесных тел они назвали музыкой сфер.
Эти идеи сделали Пифагора провидческой фигурой в философии, почти религиозным лидером, последователи которого образовали тайную секту, возможно, носившую революционный характер. Большинство пифагорейцев были рабами, поэтому их очень утешала доктрина о переселении душ, которая дарила им надежду на счастливую жизнь после смерти.

«Слепой арфист». Египет, 1579–1293 годы до н. э.
Я начал разговор с языка цифр, то есть с арифметики, затем перешел к геометрии, когда привел пример описания движения небесных тел. Переход был сделан не случайно. С точки зрения изучения форм мы следуем за природой, она дарит нам образы: кристалл, волна, овал, человеческое тело. Для описания пропорций мы опять же обращаемся к языку чисел. Пионером в этой области был гениальный Пифагор, так что, следуя его логике, я выбрал те математические дисциплины, основы которых он заложил.
Пифагор доказал, что мир звуков подчиняется последовательности целых простых чисел. Он доказывал, что и визуальный мир подчиняется тому же математическому принципу. Это заявление было поразительным! Я смотрю на чудесный красочный пейзаж Греции, на великолепие ее диких природных форм, орфических лощин и бескрайнего моря. Я спрашиваю себя: как за этой дикой красотой хаоса можно увидеть строгую числовую структуру?
Поиск ответа на мой вопрос заставляет вернуться к проблеме исходных констант, отобранных в соответствии с нашим восприятием природных законов, иначе говоря, мы должны определиться с набором эмпирических универсалий. Окружающий мир базируется на двух принципах: вертикали (силе тяжести) и линии горизонта, расположенной к ней под прямым углом. Можно свободно передвигать значения горизонтали или вертикали, не опасаясь, что пропадет прямой угол, который формируют эти две оси. Более того, я могу повернуть угол вокруг каждой из линий, все равно через четыре поворота я вернусь к прямому углу, образованному вектором силы тяжести и линией горизонта.
В визуальном плане, в вертикальной картинке, которую видит наш глаз, прямой угол определяется четырехкратным поворотом. Такое же правило действует для горизонтального мира, в котором мы передвигаемся. Представьте себе плоский мир, нанесенный на карту и сориентированный по компасу. Вот я смотрю через пролив с острова Самос на Малую Азию, прямо на юг. Я использую плашку в виде прямоугольного треугольника как указатель и направлю его вершину на юг, чтобы иметь возможность сделать четыре поворота вокруг оси. Каждый раз я буду поворачивать указатель на 90°, чтобы получить после первого поворота направление на запад, после второго – на север, после третьего – на восток, после четвертого – снова на юг. То есть, совершив оборот на 360°, вершина треугольника вновь будет указывать на Малую Азию, откуда я начал движение.
По этому принципу создан не только окружающий нас мир природы, его соблюдают все строители от доисторических времен до наших дней: вавилоняне учитывали его, когда обустраивали висячие сады; египтяне закладывали его в основу проектов, которые создавали до возведения пирамид. То есть уже в древних культурах на практическом уровне было знание, что есть плотничий (прямоугольный) треугольник, в котором правят соотношения между числами. Вавилонские строители, вероятнее всего, уже с 2000 года до н. э. знали множество формул; индейцы и египтяне – несколько меньше. Египтяне, как кажется, почти всегда использовали треугольник с соотношениями сторон 3:4:5. Однако только в 550 году до н. э. Пифагор перевел это знание из мира эмпирики в мир того, что сегодня мы называем доказательством. То есть он задал вопрос: «Каким образом цифры, образующие этот плотничий треугольник, следуют из того факта, что прямой угол – это то, что можно повернуть четыре раза так, чтобы он указал в ту же сторону?»
Доказательство Пифагора, должно быть, выглядело следующим образом (оно заметно отличается от того, которое приведено в современных школьных учебниках). Четыре высшие точки – юг, запад, север, восток – треугольников, которые образуют крест компаса, – это углы квадрата. Я сдвигаю четыре треугольника таким образом, чтобы длинная сторона каждого заканчивалась на высшей точке соседнего. Теперь я построил квадрат по самой длинной стороне прямоугольных треугольников – по гипотенузе. Чтобы понять, что является частью замкнутой области, а что нет, я заполню маленький внутренний квадрат дополнительной плиткой. (Я использую плитки, поскольку многие узоры в Древнем Риме и на Востоке основаны на этом типе связи между математическим соотношением и размышлениями о природе.)
Теперь у нас есть квадрат на гипотенузе, и мы, конечно, можем это вычислить из квадратов катетов. Но так мы не увидим естественную структуру и сущность фигуры. Нам не нужны вычисления. Просто сыграем в детскую игру, и это откроет перед нами больше любых вычислений. Переместим два треугольника на новые позиции. Подвинем треугольник, указывающий на юг, так, чтобы его гипотенуза была рядом с гипотенузой треугольника, указывающего на север. И переместим треугольник, указывающий на восток, так, чтобы его гипотенуза была рядом с гипотенузой треугольника, указывающего на запад.
Теперь мы создали L-образную фигуру с той же площадью (естественно, ведь она составлена из тех же кусочков), чьи стороны в то же время – катеты прямоугольного треугольника. Теперь я положу делитель, который отделил конец L от верхней палочки. Очевидно, что конец – это квадрат катета треугольника, а вертикальная часть L – это квадрат гипотенузы.
Пифагор доказал общую теорему: не только для египетского треугольника 3:4:5 или любого из вавилонских треугольников, а для каждого треугольника с прямым углом. Он доказал, что квадрат гипотенузы равен сумме квадратов катетов, в том и только в том случае, если треугольник содержит прямой угол. Например, стороны 3:4:5 образуют прямоугольный треугольник потому, что:
52 = 5 х 5 = 25
= 16 + 9 = 4 х 4 + 3 х 3
= 42 + 32
Это же правило действует и для вавилонского треугольника, длина сторон которого составляет от 8:15:17 до 3367:3456:4825. Без сомнения, это означает, что вавилоняне хорошо знали арифметику.
По сей день теорема Пифагора остается самой важной теоремой математики. Может показаться, что это громко сказано, но Пифагор установил фундаментальную характеристику пространства, в котором мы существуем, и впервые описал его с помощью чисел. И точность этих чисел отражает точность законов, которые управляют Вселенной. Недаром теорему Пифагора предлагают отправить к другим планетам для того, чтобы проверить, есть ли там разумная жизнь.
Дело в том, что теорема Пифагора в том виде, в каком я ее доказал, раскрывает симметрию плоского пространства. Прямой угол становится элементом симметрии, потому что делит плоскость крестообразно. Если допустить, что плоскость основана на симметрии другого рода, то теорема перестанет быть верной, а между сторонами треугольников мы обнаружим другие соотношения. И пространство – такая же важная часть природы, как материя (даже невидимая, как, например, воздух). Вот чему учит нас геометрия. При этом важно, что симметрия пронизывает всю гармонию природы.
Когда Пифагор доказал свою великую теорему, он принес жертву музам – сто волов в благодарность за вдохновение. Это был жест гордости и смирения – чувств, переполняющих каждого ученого в день, когда он достигает результата и объявляет: «Я нашел ключ к структуре самой природы».
Последователи видели в Пифагоре не только философа, но и в немалой степени религиозного лидера. Причины этого кроются в сильном азиатском влиянии, которое испытывала вся греческая культура и про которое мы частенько забываем. Мы привыкли считать Грецию частью западной культуры; но Самос, центр классической Греции, находится в миле от побережья Малой Азии. Через его порты и школы идеи восточных мудрецов достигали Греции, а спустя несколько веков, как ни странно, стали распространяться в обратном направлении – задолго до того, как попали в Западную Европу.
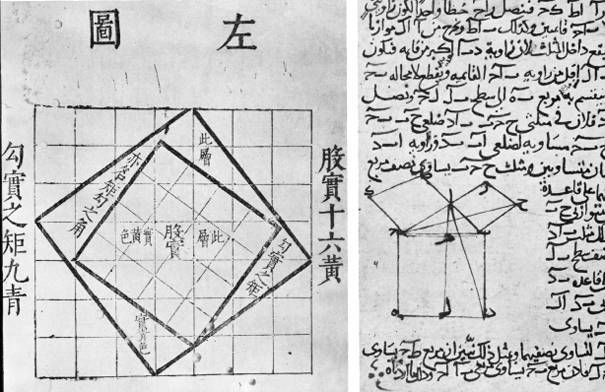
Пифагор доказал общую теорему не только для египетского треугольника с соотношением сторон 3:4:5, но и для любого другого, имеющего прямой угол.
Две записи доказательств теоремы Пифагора: китайская печатная и арабская рукописная (датируется 1258 годом)
Знания совершают потрясающие путешествия, и то, что кажется нам разрывом во времени, часто оборачивается медленным прогрессом от места к месту, от одного города к другому. Караваны везут вместе с товарами и методы торговли своих стран – единицы измерения, методы расчета, – и техники и идеи идут туда же, куда и они, через Азию и Северную Африку. Так и математика Пифагора не пришла к нам напрямую. В стройную систему ее преобразовал другой человек, живший в 300-х годах до н. э. в Александрии, крупном городе, расположенном на берегу полноводного Нила. Он же сделал эту систему известной. Имя этого человека – Евклид.
Совершенно очевидно, что он принадлежал к пифагорейской традиции и был ее бескорыстным и верным последователем. Известно, что в ответ на вопрос одного из своего учеников о практическом применении теоремы Пифагора Евклид сказал рабу: «Он хочет получить прибыль от обучения. Дай ему монетку». Порицание, возможно, было парафразом девиза пифагорейского братства, который грубо можно перевести так: «График и шаг, не график и монетка». «Шаг» здесь – это шаг вперед в познании, или то, что я называю восхождением человечества.
Влияние Евклида как модели математического рассуждения было огромным и устойчивым. Его книгу «Начала» переводили на латынь, арабский, еврейский и многие европейские языки, а по числу переизданий она уступает только Библии. Меня обучал математике человек, который все еще цитировал теоремы геометрии по числам, присвоенным им Евклидом; и пятьдесят лет назад это вовсе не было редкостью, а, наоборот, обычной вещью. В биографии Томаса Гоббса, опубликованной в 1680 году знаменитым антикваром и автором многих других биографий Джоном Обри, тот написал, что в зрелом возрасте Гоббс всерьез увлекся геометрией, после того как увидел в библиотеке издание «Начал» раскрытым на «47 Element libri I». Предложение 47 и есть знаменитая теорема Пифагора.
Астрономия была другой популярной наукой, которой охотно занимались в Александрии в начале I тыс. н. э. Свидетельство этого мы находим в библейском сюжете о том, как три мудреца следовали за светом Вифлеемской звезды. Можно сделать вывод, что эти мудрецы были звездочетами. Секрет небес, который мудрецы искали в античности, был открыт греком Клавдием Птолемеем, работавшим в Александрии около 150 года н. э. Его работы дошли до европейцев в арабских текстах, многие оригиналы были утеряны или уничтожены во время разорения Александрийской библиотеки в 389 году фанатиками-христианами, в ходе других войн и вторжений, прокатившихся по восточной части Средиземноморья в Средние века.
Модель небес, выстроенная Птолемеем, представляет собой восхитительно сложную систему, основанную на простой аналогии: Луна обращается вокруг Земли, значит, Солнце и остальные планеты делают то же самое (александрийские астрономы включали Луну и Солнце в число планет). Греки считали, что совершенная траектория есть круг, поэтому Птолемей описал круговое движение всех крупных небесных тел. Созданная им система циклов и эпициклов кажется нам простодушной и искусственной. Тем не менее она была красивым и работающим изобретением, кроме того, в нее безоговорочно верили арабы и христиане Средних веков. Система Птолемея просуществовала без малого четырнадцать столетий – гораздо дольше, чем многие современные теории.
Остановимся на минуту, чтобы понять, почему столь рано зародившаяся астрономия стала изящным и искусным прообразом физической науки. Пробудили любопытство человека сами звезды – невероятные природные объекты, с давних времен привлекавшие его внимание. Казалось бы, собственное тело должно быть для человека гораздо интереснее. Почему же астрономия опередила медицину? Почему врачи обращались к звездам, чтобы получить предсказание о благоприятных и опасных влияниях на жизнь пациента, ведь надежда на мощь астрологии – это отказ от медицины как науки? С моей точки зрения, основная причина заключается в том, что наблюдаемое движение небесных тел оказалось вычислимым и с ранних времен (скажем, III тыс. до н. э. в Вавилоне) исследовалось математически. Главенство астрономии зиждется на возможности подступиться к ней с математическим аппаратом; а прогресс в физике и – недавно – в биологии в равной мере зависел от формулировок законов, которые возможно представить в виде математических моделей.
Зачастую рождению новых идей способствует конкретный импульс. На пути восхождения человечества таким мощным импульсом стал приход ислама через шестьсот лет после рождения Христа. Мусульманство начиналось как локальное явление, но когда в 630 году Магомет завоевал Мекку, оно распространилось на юг как вихрь. За сто лет ислам дошел до Александрии, Багдада, ставшего центром ученого мира, и до Исфахана в Персии. В 730-е годы мусульманская империя простиралась от Испании и Южной Франции до Китая и Индии. Она была сильным и богатым государством, в то время как Европа погружалась во мрак Средневековья.
Мусульмане-завоеватели с пылом клептоманов начали осваивать достижения науки покоренных народов. С собой же они принесли довольно слабые простые навыки.
Например, первые купольные мечети возводились с применением инструментов, едва ли более сложных, чем угольник древнего строителя. Одна из таких мечетей – Масджид-и-Джами (Пятничная мечеть) в Исфахане действует и сегодня. Она входит в число самых ранних памятников мусульманской архитектуры. В таких центрах учение Греции и всего Востока собиралось, изучалось и видоизменялось.
Магомет установил, что ислам не должен стать религией чудес, поэтому в интеллектуальном плане он основывался на созерцании и анализе. Поклоняются адепты этой религии обезличенному и формализованному божеству, потому что мусульманская мистика держится не на крови, вине, плоти и хлебе, а на сверхъестественном, неземном экстазе.
Аллах – Свет небес и земли. Его свет в душе верующего подобен нише, в которой находится светильник. Светильник заключен в стекло, а стекло подобно жемчужной звезде. В храмах, построенных во имя Аллаха, люди будут восхвалять его утром и вечером. От молитвы во славу Господню их не отвлечет ни торговля, ни прибыль.
Одним из первых греческих изобретений, освоенным мусульманами, стала астролябия. Это примитивный астрономический инструмент, позволяющий довольно приблизительно определить высоту Солнца или звезды. Однако сопоставив единичное наблюдение с одной или несколькими звездными картами, астролябия давала сложную схему расчетов, благодаря которым можно определить широту, время восхода и заката, а также время совершать намаз или направление, в котором находится Мекка. Украшения, которые они наносили на такие карты, имели исключительно религиозный характер и подчеркивали их мистическое значение.
Долгое время астролябии служили карманными часами и логарифмической линейкой одновременно. В учебнике, составленном в 1391 году поэтом Джеффри Чосером для своего сына, он обучал его пользоваться астролябией. Основой этого пособия стал текст арабского астронома, написанный в VIII веке.
Возможность делать математические расчеты привела мавританских ученых в восторг. Они занялись математикой с огромным энтузиазмом, искали и находили множество остроумных решений, которые применяли в механических устройствах и машинах, и даже сделали в халифате Багдад в XIII веке астрологический или астрономический компьютер, напоминающий автоматический календарь. Он, конечно, не был приспособлен для серьезных вычислений, но стал свидетельством мастерства механиков и их страсти к игре с числами.
Самым главным новшеством, которое привнесли в историю цивилизации нетерпеливые и любознательные арабские ученые, стала новая система цифровой записи чисел. В Европе в то время по-прежнему пользовались римскими цифрами, неуклюжими и громоздкими. Например, число 1825 записывалось как MDCCCXXV, потому что представляло собой сумму: М = 1000; D = 500; 300 = C + C + C = 100 + 100 + 100; 20 = X + X; 5 = V. Мусульманские ученые заменили эти сложные построения современной десятичной системой, которую мы до сегодняшнего дня называем арабской. В арабском манускрипте в верхнем ряду написаны цифры 18 и 25. Мы распознаем 1 и 2 как наши родные цифры (хотя двойка стоит на кончике). Чтобы написать 1825, нужно просто поставить друг за другом четыре символа, начиная с первого, поскольку на этом месте каждый символ показывает, что он обозначает, – тысячи, сотни, десятки, единицы.
Тем не менее система, описывающая величину местом, должна предусматривать символ для обозначения пустого пространства или отсутствующей вещи. Арабским ученым принадлежит честь изобретения нуля (zero). Вместе с этой цифрой они ввели в оборот слова: шифр (cipher), алгебра (algebra), альманах (almanac), зенит (zenith) и десятки других терминов математики и астрономии. Десятичную систему исчисления арабы заимствовали в Индии в 750-х годах н. э. Европа же не признавала эту систему еще пять веков.
Огромный размер мавританской империи превратил ее в своеобразную ярмарку знаний, на которой свободно работали ученые-еретики из числа несториан на Востоке и неверных евреев на Западе. Мусульмане пытались обратить других в свою религию, но не пренебрегали их знаниями. Памятником этой замечательной эпохи мы считаем восточный персидский город Исфахан и западную Альгамбру, расположенную в Южной Испании.
По внешнему облику Альгамбра представляет собой квадратную надежную крепость, в архитектуре которой ничто не намекает на арабские формы. Чтобы увидеть ее истинное лицо, надо войти внутрь – увидишь дворец, который создан по образцу рая. Альгамбра – это позднее произведение. В ней чувствуется усталость империи, миновавшей пик своего величия, но тихой и безопасной. Молитвы в таких мечетях и дворцах стали чувственными и успокоительными. Они зазвучали, словно музыка волн, извилистые линии которых пронизывают все арабские мелодии, хотя манера пения и строй основаны на учении Пифагора о музыке. Каждый дворец, в свою очередь, – отзвук и память о мечте, сквозь которую плыл султан (ибо он не ходил, а его носили). Альгамбра – наиболее полное земное воплощение описания рая из Корана.
Именно им уготованы сады Эдема, в которых текут реки. Они будут украшены золотыми браслетами и облачены в зеленые одеяния из атласа и парчи. Они будут возлежать там на ложах, прислонившись. Замечательное вознаграждение и прекрасная обитель!
Альгамбра считается последним и самым изысканным памятником арабской цивилизации в Европе. Последний мавританский султан властвовал над этой землей до 1492 года, когда Изабелла I Кастильская уже финансировала путешествие Колумба. Обилием внутренних двориков и комнат Альгамбра напоминает пчелиные соты. Однако самой секретной считается Сала де лас Камас – одна из комнат гарема. Сюда жены и наложницы султана приходили отдыхать обнаженными после ароматических ванн. Для них играли слепые музыканты, им прислуживали евнухи. Султан наблюдал за этой сценой сверху и бросал яблоко той, что должна была провести с ним ночь.
В западной цивилизации подобное помещение было бы расписано чудесными рисунками, посвященными прекрасным женским формам, и эротическими картинками. В гареме все иначе: Коран запрещает изображать человеческое тело. Также было запрещено изучение анатомии, что заметно тормозило развитие естественных наук в арабском мире. Вместо эротических рисунков стены гарема в Альгамбре расписаны простыми геометрическими узорами. В арабской цивилизации художник был математиком. Орнаменты отражают те вершины, которых арабам удалось достичь, изучая свойства и симметрию того двумерного пространства, которое мы сегодня называем евклидовой плоскостью. Эту симметрию математически впервые описал Пифагор.
Среди огромного богатства узоров я для начала выделю один – самый простой. Он основан на ритмичном повторении мотива из двух темных горизонтальных листьев и их перекличке с аналогичными вертикальными фигурами. Бросающаяся в глаза симметрия – это параллельный сдвиг узора и либо горизонтальное, либо вертикальное его отражение. Заметьте, что арабы очень любят конструкции, в которых темные и светлые элементы рисунка идентичны. Если внимательно вглядеться, не обращая внимания на цвет, то можно увидеть, что новый лист получается, если предыдущий повернуть точно под прямым углом. Затем, не меняя оси вращения, опять повернем лист на 90° – 9 получим третью фигуру, снова поворот – и мы получили четвертую фигуру. Подобное вращение очень гармонично и правильно закручивает весь орнамент: каждый лист в орнаменте прибывает на расположение другого листа, как бы далеко от центра вращения он ни отстоял.
Отражение по горизонтали – это двусторонняя симметрия цветного узора, и таково же отражение по вертикали. Но если игнорировать цвета, мы увидим четырехстороннюю симметрию. Она получается четырехкратным поворотом фигуры на 90°.

Точно так же мы с вами раньше доказали теорему Пифагора, поэтому нераскрашенный орнамент своей симметрией напоминает пифагоров квадрат.
Теперь обратимся к более тонким рисункам: четырехцветные треугольные фигуры, похожие на флаги на ветру, отображает один очень простой вид симметрии, в двух направлениях. Можно сдвинуть раппорт по вертикали или по горизонтали. Волнистость здесь также играет роль. Редко можно найти узор, который не допускает отражения, потому что все треугольники поворачиваются вправо, а отражение развернуло бы их влево.
Теперь рассмотрим подробно все треугольные фигуры, чтобы понять, чем они различаются между собой. Во-первых, эти элементы образуют две большие группы, разделяемые по тону, – темную и светлую. Мы видим также симметрию вращения. Сосредоточьте внимание на центре, в котором сходятся вершины всех шести фигур. Обратите внимание, что светлая и темная фигуры чередуются. Темный треугольник можно повернуть так, чтобы он занял положение следующего темного треугольника, затем следующего и, наконец, вернулся в исходное положение, – тройная симметрия, вокруг которой вращается весь узор.

Но это не все возможные виды симметрии. Забудьте про цвет совсем. Обратите внимание: мы можем повернуть фигуру вокруг центра, потому что все треугольники одинаковы по форме. Это шестерная симметрия, которая изучена нами лучше всего, так как это симметрия снежинки.
Тут нематематик имеет право спросить: «Извините, конечно, но какое отношение все это имеет к математике? Неужели серьезные арабские мыслители тратили свое драгоценное время на такие игры, не говоря уже о современных ученых?» Дам неожиданный ответ: это не игра. Подобные эксперименты помогают понять то, с чем мы сталкиваемся ежедневно и ежечасно, потому что живем в трехмерном мире и все категории этого пространства неразрывны. Решая простые двумерные задачи, связанные с рисунками, мы открываем потаенные законы, управляющие нашим пространством. Они прежде всего касаются определенных видов симметрии, которые существуют не только в искусственных моделях. Они заложены в фундаментальные основы жизни, созданные самой природой, – в структуры атомов.
Наиболее явно эти структуры можно отследить в кристаллах. Посмотрите на необработанный исландский шпат. Вы удивитесь и невольно зададите себе вопрос: почему он имеет такую правильную форму? Почему его грани плоские? Но таковы кристаллы; мы привыкли видеть их правильными и симметричными, но почему? Они не сделаны человеком, такими их создает природа. Двумерная плоскость позволяет понять, как материя образуется из атомов, которые собираются в структуры один к одному. В конечном итоге они складываются в узоры, похожие на симметричные мавританские орнаменты, которые я проанализировал.
Возьмите, например, красивый куб пирита или самый изысканный кристалл флюорита, имеющий восьмигранную форму (кстати сказать, это также естественная форма алмаза). Их симметрия обусловлена трехмерностью пространства, в котором мы живем. И никакие структуры, созданные атомами, не могут нарушить этот важнейший закон природы. Как элементы узора, атомы в кристалле укладываются во всех направлениях. Таким образом, кристалл, как и узор, должен иметь форму, которая может расширяться или повторяться во всех направлениях до бесконечности. Вот почему грани кристалла могут иметь только определенные формы – в паттерне есть только симметрия. Возможна двусторонняя, четырехсторонняя, шестисторонняя симметрия и не более. Но не пятисторонняя. Вы не можете сделать так, чтобы атомы образовали пять треугольников, которые одновременно вписались бы в пространство.
Разработка различных орнаментов и исследование на практике возможностей симметрий пространства (по крайней мере в двух измерениях) стали великими достижениями арабских математиков. И у того мира есть замечательная законченность. Султан, обнаженные наложницы, евнухи и слепые музыканты создали замечательный формальный узор, в котором исследование существующего было идеальным, но который не менялся. По этой причине развитие мысли остановилось до тех пор, пока не пришло время для нового шага в восхождении человека.
Христианство начало отвоевывать свои позиции, и точкой отсчета стала Северная Испания с начала I тыс. н. э., точнее деревня Сантильяна, расположенная на прибрежной полосе, которую мусульмане не завоевали. Религиозность крестьян выражалась в простых изображениях, украшавших стены сельской церкви, – вола, осла, Агнца Божьего. Анималистические сюжеты были немыслимы в мусульманском искусстве. И не только изображения животных были разрешены; Божий сын – это ребенок, а Богоматерь – женщина и объект обращения с личной молитвой. Когда мы видим статую Девы Марии в процессии, мы попадаем в другую Вселенную: не абстрактных узоров, а жизни во всей ее полноте.
Когда христианство отвоевало Испанию обратно, возник замечательный калейдоскоп. Мусульмане, христиане и иудеи смешались и создали удивительную культуру из разных вероисповеданий. Плавильным котлом для них в 1085 году стал город Толедо. Отсюда в христианскую Европу попадали все классические труды, которые арабы привезли из Греции, Ближнего Востока и Азии.
Мы привыкли считать, что родина Возрождения – Италия. Однако зерно этой великой эпохи проросло в XII веке в знаменитой испанской школе переводчиков, расположенной в Толедо. Ее наставники и ученики переводили на латынь с забытого Европой греческого языка через арабский и иврит работы выдающихся древних ученых. В Толедо, среди других интеллектуальных нововведений, появились первые астрономические таблицы, энциклопедии звездного неба. Что характерно, таблицы составлялись в соответствии с христианскими канонами, но числа были записаны арабскими цифрами, что делает их почти современными.
Самый блестящий и наиболее известный из переводчиков – Герард Кремонский, который приехал в Толедо из Италии, чтобы отыскать копию книги Птолемея «Альмагест». Увидев кроме нужного фолианта труды Архимеда, Гиппократа, Галена, Евклида и других классиков греческой науки, он решил остаться в городе и перевести эти тексты на латынь.
Однако лично для меня самым замечательными, оказавшими влияние на дальнейшее развитие европейской и мировой науки стали переводы трудов человека, имевшего отнюдь не греческое происхождение. Я обратил на него внимание, потому что именно он понял, как важно воспринимать вещи в объеме. Ведь именно в этом вопросе греки тотально заблуждались. Этот человек, араб по происхождению, чей ум отличали оригинальность и смелость, жил в начале I тыс. до н. э., мы зовем его Альхазен. Его настоящее имя – Ибн аль-Хайсам. Греки думали, что свет поступает от глаз к объекту. Альхазен первым установил, что предмет отражает падающие на него лучи, которые человеческий глаз только воспринимает. Греки не могли объяснить, почему кажется, будто при движении размеры объекта (например, моей руки) изменяются. Арабский ученый ясно понял, что конус лучей, отражающихся от моей руки, будет становиться у́же по мере того, как я стану отодвигать ее от вас. Если же я приближу руку к вам, пучок света, попадающий в ваши глаза, расширится. Это настолько просто, что удивительно, как ученые могли не уделять этому внимание (Роджер Бэкон здесь исключение) в течение почти 600 лет. Зато идею отраженного пучка лучей гораздо раньше оценили живописцы. Они построили на ней учение о перспективе. А перспектива – это новая идея, благодаря которой математика сейчас переживает расцвет.
Перспектива проникла в творчество художников Северной Италии, Флоренции и Венеции, в XV веке. Труд Альхазена «Книга оптики», перевод которого хранился в библиотеке Ватикана, снабжен комментариями Лоренцо Гиберти, автора великолепных бронзовых врат во флорентийском баптистерии. Но следует сказать, что он не был первым, кто исследовал перспективу. Вероятнее всего, первым к таким опытам приступил великий итальянский скульптор и архитектор Филиппо Брунеллески, который стремился не только реалистично показать объект, но и сохранить ощущение движения в пространстве.
Прогресс очевиден, особенно если сравнить картины, построенные на перспективе, с более ранними произведениями. Вспомните, например, полотно Витторе Карпаччо, где святая Урсула изображена в венецианском порту (1495 год). Художник сумел передать трехмерность пространства, – точно так же объем и глубина появились в новом звучании европейской музыки. Но важнее то, что в картине, как и в музыкальных гармониях, появилась динамика. Обитатели картины подвижны, и мы видим, что глаз художника следит за их движением.
Для сравнения возьмем фреску Флоренции, написанную за столетие до того, где-то в 1350 году. Это взгляд на город из-за стены, и художник несколько наивно смотрит через стены и крыши домов, которые будто бы расположены ярусами. Но дело здесь не в нехватке мастерства. В середине XIV века канон обязывал живописцев изображать предметы такими, какие они есть, а не как они выглядят. Это взгляд Бога, карта вечной истины.
У художника, использующего перспективу, иные намерения. Он сознательно уводит нас от абсолюта и абстрактного взгляда. Для нас фиксируется не место, а момент, и момент скоротечный: больше точка зрения во времени, а не в пространстве. Все это было достигнуто с помощью точных математических инструментов. Их применение скрупулезно зафиксировал немецкий художник Альбрехт Дюрер, приехавший в 1506 году в Италию, чтобы обучиться «секретному искусству перспективы». Конечно, Дюрер и сам фиксировал моменты времени; если мы воссоздадим обстановку, то увидим, как художник выбирает драматический момент. Вот он идет вокруг модели, останавливается. Идет дальше, замирает. Как фотозатвор, он щелкает в самый сильный момент, когда видит, как раскрывается модель. Для художника перспектива не просто точка обзора, а активное и непрерывное действие.
Сначала обычным делом было использовать прицел и сетку, чтобы удержать мгновение. Прицельное устройство пришло из астрономии, а расчерченная на квадраты бумага, на которой рисовали картину, теперь незаменимое подспорье в математике. Вспомните работу Дюрера «Поклонение волхвов». Художник нашел удивительные средства, чтобы передать ощущение реальности происходящего здесь и сейчас: румянец на щеках Богоматери, изображение вола и осла на дальнем плане. Три мудреца с востока нашли свою звезду, и она знаменовала рождение новой эпохи.
Обратите внимание на чашу, помещенную Дюрером в центр полотна; она была образцом для преподавания перспективы. Например, у нас есть детальный рисунок чаши Учелло; мы можем воссоздать его на компьютере. Его глаз работал, как вращающаяся платформа, исследуя меняющуюся форму, то, как круги вытягиваются в овалы, и ловя момент времени как след в пространстве.
Анализ движения объекта и его изменения, который я делаю на компьютере, был чужд греческим и мусульманским умам. Они всегда искали неизменность и статичность, вневременной мир идеального порядка. Верхом совершенства они считали круг, который сделали траекторией движения всех предметов, что обеспечивало гармонию сфер. По этой причине система Птолемея была построена из кругов, благодаря чему время текло равномерно и невозмутимо.
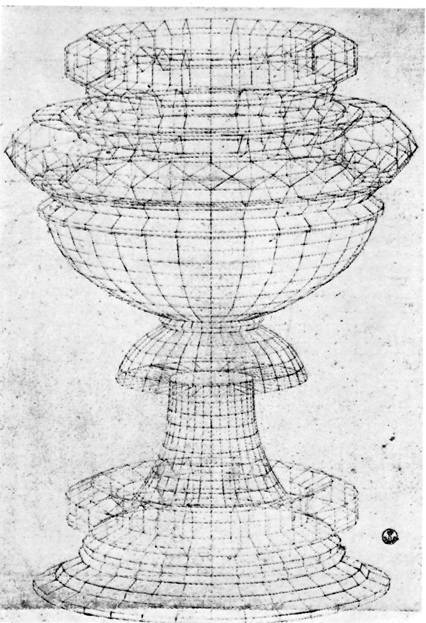
Момент времени как след в пространстве.
Паоло Учелло. Детальный рисунок чаши
В реальном мире движения не могут быть одинаковыми: они изменяют направление и скорость в каждый момент времени, поэтому величины, которыми мы обозначаем их значения, должны быть переменными. Это теоретическая проблема для небес, но вполне реальная и насущная для земли. Нам нужно рассчитывать полет снаряда, рост растения, падение капли воды – процессы, которые сопровождаются резкими изменениями формы и направления движения. Живописцы Ренессанса не имели технических средств, чтобы запечатлеть каждый конкретный момент времени. Однако у них были другие, не менее совершенные инструменты – внутреннее зрение художника и математическая логика.
После 1600 года Иоганн Кеплер укрепился в мысли, что планеты не движутся однотипно по кругу. Их траектории всегда имеют формы эллипса, потому что разные участки пути небесные тела проходят на разных скоростях. Тогда же он пришел к выводу, что старая математика, ориентированная на равномерное движение статических моделей, не работает и ученым нужен новый инструментарий, позволяющий изучать движение в каждый конкретный момент времени.
Математические методы, которые позволили изучать моментальное движение, были изобретены двумя гениями XVII века – Исааком Ньютоном и Готфридом Вильгельмом Лейбницем. Это сегодня мы воспринимаем время как неотъемлемую характеристику природы, но так было не всегда. Именно эти двое привнесли в науку понятия «касательная», «ускорение», «наклон», «бесконечность», «дифференциал». Началось все с забытого нынче слова – флюксия. Его придумал Ньютон. Сегодня мы называем это математическое понятие производной, и оно действительно оказалось лучшим инструментом для определения временно́го потока. Лейбниц на основании флюксий разработал дифференциальное исчисление. Однако воспринимать и изобретение производных, и внедрение дифференциалов только как методологические усовершенствования – значит упустить их реальное содержание. С появлением в математике этих двух идей наука стала зеркалом движения человеческой мысли, что позволило человечеству осознать свое творческое, созидательное начало. Эти изобретения стали еще одним шагом на пути восхождения человека. Техническая сторона дела, которая во многом определяет результат, как ни странно, представляется величиной бесконечно малой. Смысл и масштаб этих открытий осознаешь после того, как оцениваешь, какой интеллектуальный прорыв совершили Ньютон и Лейбниц. Мы оставим профессионалам обсуждение технической стороны их изобретений, а назовем ее математикой перемен.
Законы природы всегда описывались числами с тех самых пор, как Пифагор сказал, что числа – это язык природы. Но теперь язык природы должен был включить числа, которые описывали бы время. Законы природы становятся законами движения, а природа становится не серией статичных картинок, а процессом.

