Интродукция: музыко-логическое приношение

Автор:

КОРОЛЬ ПРУССИИ Фридрих Великий пришел к власти в 1740 году. Исторические трактаты упоминают о нем в основном как о проницательном и умелом полководце - однако, кроме военной деятельности, Фридрих Великий в немалой степени посвящал себя жизни умственной и духовной. Его двор в Потсдаме был центром интеллектуальной деятельности Европы восемнадцатого столетия. Прославленный математик Леонард Эйлер провел там двадцать пять лет. Многие математики, ученые и философы посетили в то время Потсдам; Вольтер и Ламеттри написали там некоторые из своих важнейших сочинений.

Но настоящей любовью короля была музыка. Сам он был страстным флейтистом и композитором; некоторые его сочинения исполняются иногда по сей день. Фридрих Великий был одним из первых покровителей искусств, признавших замечательные качества только что изобретенного фортепиано («тихогрома», как когда-то пытались окрестить этот инструмент в России). Фортепиано было изобретено в первой половине восемнадцатого века; оно представляло из себя не что иное, как модификацию клавесина. Дело в том, что на клавесине невозможно было варьировать громкость; все звуки получались одинаковыми. Тихогром, как показывает само название, был выходом из положения.

Зародившись в Италии, где Бартоломео Кристофори изготовил первое фортепиано, идея тихогрома распространилась широко. Готтфрид Зильберман, лучший мастер того времени по изготовлению органов, получил заказ на изготовление «совершенного» фортепиано. Фридрих Великий, без сомнения, явился самым большим энтузиастом этого начинания; говорят, что он приобрел целых пятнадцать инструментов, сделанных Зильберманом!

Бах

Король был горячим поклонником не только фортепиано; его вниманием пользовался также органист и композитор по имени И. С. Бах. Баховские композиции были довольно интересны; некоторые считали их напыщенными и запутанными, в то время как другие ценители восхищались ими как несравненными шедеврами. Однако никто не оспаривал способности Баха исполнять импровизации на органе. В то время умение импровизировать, наравне с исполнительским мастерством, считалось необходимым качеством органиста, а Бах имел славу превосходного импровизатора. (Прелестные рассказы о Баховских импровизациях читатель может найти в книге Дэвида и Менделя «Баховская хрестоматия» (David & Mendel, «The Bach Reader».))

В 1747 году слава 62-летнего Баха докатилась до Потсдама. Там же очутился и один из его сыновей, Карл Филипп Эмануэль Бах, ставший капельмейстером при дворе короля Фридриха. В течение нескольких лет король деликатно намекал Филиппу Эмануэлю, насколько приятен был бы Его Величеству визит в Потсдам Баха-старшего. В особенности Фридриху хотелось, чтобы Бах опробовал его новые рояли Зильбермана, которые, как он правильно предвидел, были началом больших перемен в музыке. Это королевское желание, однако, долго не исполнялось.

При дворе Фридриха Великого были обычаем вечерние концерты камерной музыки. В концертах для флейты часто солировал сам монарх. Я привожу здесь репродукцию картины немецкого художника Адольфа фон Менцеля, кто в 1800-х годах написал серию произведений из жизни Фридриха Великого. На клавесине играет К. Ф. Э. Бах; крайний справа - Иоахим Кванц, учивший короля игре на флейте и единственный, кому было даровано право исправлять ошибки в игре Его Величества. Однажды майским вечером 1747 года на королевский концерт явился неожиданный гость. Иоганн Николаус Форкель, один из первых биографов Баха, рассказывает эту историю так.

Однажды вечером, когда король уже достал свою флейту и все музыканты были готовы, вошел слуга со списком новоприбывших гостей. Не выпуская флейты из рук, король стал проглядывать список; вдруг он быстро повернулся к собравшимся музыкантам и взволнованно воскликнул: «Господа, приехал старый Бах!» Флейта была отложена, и Баха, остановившегося у сына, тут же пригласили во дворец. Вильгельм Фридеман Бах, сопровождавший своего отца, передал мне эту историю, и, должен признаться, я до сих пор вспоминаю его рассказ с удовольствием. В то время в моде были многословные и цветистые любезности. Первое появление Баха, даже не успевшего сменить дорожное платье, перед Его Величеством, разумеется, сопровождалось пышными и изысканными извинениями. Не буду останавливаться на них подробно; замечу лишь, что в устах Вильгельма Фридемана они представляли из себя настоящий формальный диалог между Королем и Приносящим Извинения.

Самым главным, однако, было то, что король отложил свой вечерний концерт и пригласил Баха, уже тогда известного как «старый Бах», опробовать Зильбермановские фортепиано, стоявшие в нескольких залах дворца. (Здесь Форкель делает сноску: «Фортепиано, изготовленные Зильберманом из Фрейбурга, так понравились королю, что он решил скупить их все. Его коллекция насчитывала пятнадцать инструментов. Говорят, что все они, ныне непригодные, еще хранятся по углам королевского дворца.»)

Бах был приглашен играть свои импровизации; музыканты сопровождали его из залы в залу. Спустя некоторое время он предложил королю предоставить ему тему для фуги, чтобы обработать ее тут же, без подготовки. Результат привел короля в восторг. Возможно, чтобы узнать, каковы пределы импровизаторского мастерства Баха, Фридрих Великий выразил желание услышать фугу с шестью облигатными голосами. Так как не всякая тема подходит к такой полной гармонии, Бах выбрал тему сам и тут же сыграл на нее фугу так же блистательно и легко, как и на королевскую тему, чем поразил всех присутствующих.

Его Величество захотел затем услышать игру Баха на органе; на следующий день Баху пришлось совершить турне по всем органам Потсдама, так же как накануне - по всем Зильбермановским фортепиано.

После своего возвращения в Лейпциг Бах обработал тему, данную ему королем, создав трехголосную и шестиголосную композиции. К ним он добавил несколько искусных проведений темы в форме строгого канона, назвал свое произведение «Музыкальным приношением» и посвятил его автору темы.

Рис. 2. Адольф фон Мензель. «Концерт флейтистов в Сансуси».

Рис. 3. Королевская Тема.

Посылая королю «Музыкальное приношение», Бах приложил к нему письмо-посвящение, интересное уже самим своим стилем, смиренным и льстивым. С нынешней точки зрения это кажется смешным. Письмо это также дает некоторое представление о стиле Баховских извинений перед королем за свой «непрезентабельный» вид во время их первой встречи.

ВСЕМИЛОСТИВЕЙШИЙ ГОСУДАРЬ,

В глубочайшем смирении я осмеливаюсь посвятить Вашему Величеству музыкальное приношение, наилучшая часть коего создана Августейшей рукой Вашего Величества. С благоговейным и счастливым трепетом я вспоминаю особую королевскую милость, когда, во время моего визита в Потсдам, Ваше Величество собственной персоной снизошли до того, чтобы сыграть на клавире тему для фуги, и тогда же всемилостивейше поручили мне развить эту тему в присутствии Вашего Августейшего Величества. Со смирением повиновался я тогда высочайшему повелению. Однако очень скоро я заметил, что за недостатком специальной подготовки я был не в состоянии выполнить это задание так, как того требовала сия превосходная тема Засим я решился и с готовностию посвятил себя работе над более полным развитием прекрасной Королевской темы с тем, чтобы сделать ее известной всему миру По мере своих сил я исполнил это решение, движимый желанием прославить, хотя бы в ничтожной степени, Монарха, чье величие и могущество, как в науках военных и мирных, так и в музыке, достойно восхищения и преклонения каждого. Осмелюсь смиренно просить Ваше Величество снизойти до принятия моего скромного труда и продолжить дарить Августейшую милость

Его покорнейшему и смиреннейшему слуге

АВТОРУ.

Лейпциг, 7 июля 1747

Спустя двадцать четыре года после смерти Баха (он умер в 1750 году) барон по имени Готфрид ван Свитен, кому, кстати, Форкель посвятил свою биографию Баха, а Бетховен — свою Первую симфонию, имел беседу с королем Фридрихом. Барон вспоминает об этом так:

Он (Фридрих) говорил со мной, среди прочего, о музыке и о великом органисте по имени Бах, проведшем некоторое время в Берлине. Речь шла о Вильгельме Фридемане Бахе Я сказал, что этот музыкант наделен талантом, по глубине понимания гармонии и по исполнительской мощи превосходящим все, о чем я слышал и что я могу себе вообразить; те же, кто знавал его отца, утверждают, что тот был еще более велик. Король согласился с этим мнением и в подтверждение спел мне хроматическую тему для фуги, которую он когда-то дал старому Баху; по его словам, Бах тогда же, не сходя с места, превратил эту тему в фугу, сначала для четырех, потом для пяти и, наконец, для восьми голосов.

Сейчас уже невозможно сказать, кто украсил случившееся фантастическими подробностями — Фридрих Великий или барон Ван Свитен. Однако этот случай показывает, что уже в то время Бах стал легендарной личностью. Представление о том, насколько удивительна шестиголосная фуга, дает тот факт, что среди 48 прелюдий и фуг «Хорошо темперированного клавира» встречаются только две пятиголосные фуги. Шестиголосных фуг там нет. Импровизацию такой фуги можно, пожалуй, сравнить с сеансом одновременной игрой в шахматы вслепую на шестидесяти досках, где мастер побеждает во всех партиях! Импровизация же восьмиголосной фуги находится за пределами человеческих возможностей.

В рукописи, которую Бах послал Фридриху Великому, на странице, предшествующей нотам, была следующая надпись:

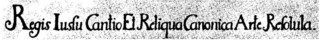
Рис. 4. Акростих Баха «РИЧЕРКАР».

(«По повелению Короля мелодия и дополнение разрешены каноническим искусством».) Здесь Бах играет со словом «канонический», обозначающим не только «при помощи канонов», но также «наилучшим образом». Начальные буквы этой надписи составляют итальянское слово

RICERCAR

(РИЧЕРКАР), означающее «искать», «исследовать». Действительно, «Музыкальное приношение» представляет собой достойный объект для исследования! Оно состоит из трехголосной и шестиголосной фуг, десяти канонов и триосонаты. Музыковеды считают, что трехголосная фуга, скорее всего, та самая, которую Бах симпровизировал для короля. Шестиголосная фуга — одна из самых сложных Баховских композиций; она основана, конечно же, на Королевской теме. Читатель найдет эту знаменитую тему на рис. 3. Она очень сложна, ритмически причудлива и полна хроматизмов (то есть звуков в другой тональности). Для среднего музыканта было бы нелегко написать даже приличную двухголосную фугу, основанную на такой теме.

Обе фуги носят у Баха название «ричеркар» — это слово было также старинным названием музыкальной формы, известной сейчас как фуга. Во времена Баха название «фуга» стало стандартным; термин же «ричеркар» приобрел новое значение. Теперь он обозначал изощренную, сложную фугу, возможно, слишком холодную и интеллектуальную для среднего слушателя. Подобное значение сохранилось и в других языках; французское (употребляющееся также и в английском) «recherche» означает что-то необычное и имеет смысловой оттенок эзотеричности и утонченной интеллектуальности.

Трио-соната — приятный отдых от холодной строгости фуг и канонов; она мелодична и радостна и местами звучит как танцевальная музыка. Однако и эта соната основана все на той же Королевской Теме! То, что Бах сумел использовать эту строгую по форме тему для такой приятной интерлюдии, похоже на чудо.

Десять канонов «Музыкального приношения» находятся в числе самых сложных канонов, написанных когда-либо Бахом. Любопытно, однако, что они не закончены. Это было сделано умышленно; каноны были своего рода головоломками, которые Бах задал королю. В те дни была популярна следующая музыкальная игра; давалась тема и вместе с ней — несколько «подсказок», в свою очередь довольно непростых. Играющие должны были «найти» канон, основанный на этой теме. Чтобы понять, как это возможно, читатель должен знать кое-что о канонах.

Каноны и фуги

Идея канона заключается в том, что одна и та же тема играется на фоне самой себя: «копии» темы повторяются в нескольких голосах. Существуют разные способы построения канонов; самые простые каноны — круговые, такие как «Дядя Ваня». Тема здесь начинается в первом голосе — спустя определенное время вступает второй голос, исполняя «копию» темы. Через то же время вступает третий голос, в свою очередь имитируя тему, и так далее. При этом все голоса исполняют тему в одной и той же тональности. Большинство мелодий не будут гармонировать сами с собой таким образом; для того, чтобы тема могла служить основой канона, каждая ее нота должна быть способной исполнять как минимум две роли: во-первых, быть частью мелодии и, во-вторых, быть частью гармонизации этой же мелодии. В трехголосном каноне, например, каждая нота темы должна к тому же участвовать в двух различных гармонизациях. Таким образом, каждая нота канона имеет несколько музыкальных значений; ухо и мозг слушателя автоматически выбирают нужное значение, исходя из контекста.

Разумеется, существуют и более сложные типы канонов. На следующей ступеньке находятся такие каноны, в которых копии темы отстоят друг от друга не только по времени, но и по тональности скажем, первый голос начинает с ноты до, а второй голос, накладываясь на первый, вступает на четыре ступени выше, с соль. Третий голос вступает опять на кварту выше, с ре, в свою очередь накладываясь на первый и второй голоса… Следующая ступень сложности — каноны, в которых голоса исполняют мелодию в разном темпе, второй голос, например, вдвое быстрее или вдвое медленнее первого. Этот прием называется, соответственно, уменьшением или увеличением, и дает эффект сокращения или растягивания мелодии.

Это еще не все! Еще более сложные каноны используют обращенную тему, «копия» мелодии обращает все восходящие ходы в нисходящие, сохраняя в них те же интервалы. Это довольно странное музыкальное преобразование; однако, привыкнув к звучанию обращенных тем, слушатель находит их вполне естественными. Бах особенно любил обращения и часто использовал их в своих композициях — «Музыкальное приношение» в этом смысле не составляет исключения. (Примером обращенного канона является «Good King Wenceslas» Скотта Кима, приведенный на рис. 4а.)

Рис. 4а. Канон «Добрый король Венсеслас».

Пожалуй, самая причудливая из всех «копий» — «пятящаяся», в которой тема играется «задом наперед», с конца к началу. Канон, использующий этот прием, известен во многих языках под ласковым прозвищем «ракоход» или «крабий канон», поскольку он запечатлевает в музыке особенности походки этих милых созданий. Нет нужды говорить, что в Баховском «Музыкальном приношении» есть ракоход (крабий канон). Обратите внимание на то, что каждый тип «копии» полностью сохраняет информацию, заложенную в первоначальной теме; это значит, что эта тема может быть легко восстановлена по любой своей копии. Такая сохраняющая информацию трансформация часто называется изоморфизмом; в этой книге мы еще не раз обратимся к изоморфизмам разного рода.

Иногда бывает желательно ослабить строгость канонической формы. Немного отступив от точного копирования темы, можно достигнуть более полной гармонии. Некоторые каноны имеют к тому же «свободные» голоса, не повторяющие тему, а просто состоящие в приятном согласовании с «каноническими» голосами.

Каждый канон «Музыкального приношения» построен на вариации Королевской темы; при этом Бах выжимает все возможное из замысловатых приемов, описанных выше. Иногда композитор даже комбинирует несколько из них в развитии одной темы. Например, в одном из трехголосных канонов «Приношения» под названием «Canon per Augmentationem, contario Motu» средний голос является свободным и исполняет Королевскую тему, в то время как два других голоса канонически «танцуют» выше и ниже Королевской темы, используя приемы увеличения и обращения. Другой канон носит загадочное название «Quaerendo invenietis» («Ищущий обрящет»). Все канонические головоломки Баха были решены; ответы на них нашел один из его учеников. Иоганн Филипп Кирнбергер. Однако читатель может попытаться найти и другие решения; очень вероятно, что возможности загадочных канонов Баха еще не исчерпаны до конца!

Теперь я должен вкратце объяснить, что такое фуга. Фуга похожа на канон тем, что основная мелодия и ее имитации исполняются несколькими голосами в различных тональностях, а также иногда в разном темпе, снизу вверх или от конца к началу. Однако фуга гораздо менее строга по форме, чем канон, что придает ей больший артистизм и эмоциональность. Безошибочной определяющей приметой фуги является её начало: один голос исполняет тему до конца. Затем вступает второй голос, четырьмя тонами выше или тремя тонами ниже. Первый голос в это время ведет дополнительную тему, подобранную так, чтобы дать ритмический, гармонический и мелодический контраст к основной теме. Последующие голоса вступают по очереди, исполняя основную тему, часто являющуюся аккомпанементом дополнительной темы; остальные голоса в это время занимаются тем, что, следуя прихотливой фантазии композитора, «украшают» фугу различными мелодиями. Когда все голоса «прибывают» к концу темы, правил больше не существует. Существуют, конечно, некоторые типичные приемы; но они не настолько стандартны, чтобы по ним, как по формулам, можно было бы строить фуги. Две фуги из «Музыкального приношения» — яркий пример композиций, которые никогда не могли бы быть «сочинены по формулам». В них есть нечто гораздо более глубокое, чем простая «фугообразность».

В целом, «Музыкальное приношение» - одно из высших достижений Баха в области контрапункта. Оно само по себе является одной большой интеллектуальной фугой, где переплетаются множество идей и форм и на каждом шагу встречаются шутливые иносказания и тонкие намеки. Это прекрасное создание человеческого ума, которым мы не устанем восхищаться. (Все произведение замечательно описано в книге X. Т. Дэвида «Музыкальное приношение» И. С. Баха (Н.T.David, «J.S.Bach's Musical Offering»).

Естественно растущий канон

Один из канонов «Музыкального приношения» особенно необычен. Это трехголосный канон под названием «Canon per tonos» («Тональный канон»). Самый высокий голос исполняет Королевскую тему; два других голоса дают каноническую гармонизацию, основанную на второй теме, причем нижний голос ведет свою мелодию в до миноре (общая тональность всей фуги), а верхний - ту же мелодию, но на пять ступеней выше. Отличительным свойством этого канона является то, что в конце — или, вернее, когда нам кажется, что канон заканчивается — его тональность меняется с до минора на ре минор. Бах каким-то образом ухитряется смодулировать (поменять тональность) прямо под носом слушателей! Канон сконструирован таким образом, что его кажущийся финал неожиданно плавно переходит в начало; этот процесс можно повторить, придя на этот раз к тональности ми минор, которая в свою очередь оказывается началом! Эти последовательные модуляции уводят слушателя во все более далекие тональные «провинции», так что после нескольких из них он чувствует себя уже безнадежно далеко от начальной тональности. Однако, чудесным образом, после шести модуляций мы возвращаемся все к тому же до минору. Все голоса теперь звучат ровно на октаву выше, чем в начале - пьеса может быть естественным образом прервана на этом месте. Вы можете подумать, что Бах именно это и намеревался сделать — однако Бах, несомненно, упивался возможностью продолжать этот процесс бесконечно. Может быть, поэтому он и написал на полях «Пусть Королевская слава возрастает подобно этой модуляции». Чтобы подчеркнуть заложенную в описанном каноне возможность естественного бесконечного движения, я буду называть его «Естественно Растущий Канон».

В этом каноне Баха мы впервые сталкиваемся с примером «Странных Петель». «Странная Петля» получается каждый раз, когда, двигаясь вверх или вниз по уровням иерархической системы, мы неожиданно оказываемся в исходном пункте. (В нашем примере это система музыкальных тональностей.) Иногда, описывая систему со Странной Петлей, я использую термин Запутанная Иерархия. В дальнейшем тема Странных Петель прозвучит еще не раз. Иногда она будет спрятана, а иногда будет лежать на поверхности; иногда она будет проводиться слева направо, иногда — вверх ногами, а иногда — ракоходом. Мой совет читателю — «Quaerendo invenietis».

Эшер

Как мне кажется, самые яркие и впечатляющие зрительные реализации идеи Странных Петель представлены в работах голландского графика М. К. Эшера, жившего с 1898 по 1971 год Эшер был создателем одних из самых интеллектуально стимулирующих рисунков всех времен Многие из них берут свое начало в парадоксе, иллюзии или двояком значении. Среди первых поклонников графики Эшера оказались математики, это неудивительно, так как его рисунки часто основаны на математических принципах симметрии или структуры. Однако типичный рисунок Эшера представляет из себя нечто гораздо большее, чем только лишь симметрию или определенную структуру часто в его основе лежит некая идея, представленная в художественной форме В частности, Странная Петля - одна из наиболее часто повторяющихся в работах Эшера тем. Взгляните, например, на литографию «Водопад» (рис. 5) и сравните ее бесконечно спускающуюся шестиступенчатую Петлю с бесконечно поднимающейся шестиступенчатой Петлей «Тонального канона». Сходство поистине удивительное! Бах и Эшер проводят одну и ту же тему в двух различных «ключах»: музыка и изобразительное искусство.

Рис. 5. М. К. Эшер. «Водопад».

В работах Эшера встречаются различные типы Странных Петель: они могут быть расположены по порядку в зависимости от того, как туго они «затянуты». Литография «Подъем и спуск» (рис. 6), на которой монахи плетутся по лестнице, навсегда уловленные Петлей, является самой свободной версией, так как Петля здесь содержит множество ступеней.

Рис. 6. М. К. Эшер. «Подъем и спуск».

Более «тугая» Петля представлена в «Водопаде», который, как мы уже видели, содержит всего шесть ступеней. Читатель может возразить, что понятие «ступени» весьма неопределенно: к примеру, можно считать, что «Подъем и спуск» имеет не сорок восемь (ступеньки), а всего четыре (лестничные клетки) уровня.

Рис. 7. М. К. Эшер. «Рука с зеркальным шаром».

Рис. 8. М. К. Эшер. «Метаморфоза II».

Действительно, подсчету ступеней-уровней всегда свойственна некоторая неопределенность; это верно не только для картин Эшера, но и для любых многоступенчатых иерархических систем. Позже мы постараемся глубже понять причину этой неопределенности. Однако не будем отвлекаться! Если затянуть Петлю еще туже, мы получим замечательную картину «Рисующие руки» (рис. 135), на которой каждая из рук рисует другую — двуступенчатая Странная Петля. Наконец, самая тугая Петля представлена в «Картинной галерее»(рис. 142): это картина картины, содержащей саму себя. Или это картина галереи, содержащей саму себя? Или города, содержащего самого себя? Или молодого человека, содержащего самого себя? (Между прочим, иллюзия, лежащая в основе «Подъема и спуска» и «Водопада» была изобретена не Эшером, а английским математиком Роджером Пенроузом в 1958 году. Однако тема Странных Петель появилась в работах Эшера уже в 1948 году, когда он создал свои «Рисующие руки» «Картинная галерея» датируется 1956 годом.)

В концепции Странных Петель скрыта идея бесконечности, ибо что такое Петля, как не способ представить бесконечный процесс в конечной форме? Бесконечность играет важную роль во многих картинах Эшера. Копии какой-либо «темы» часто «вставлены» друг в друга, создавая зрительные аналогии с канонами Баха. Несколько таких структур можно увидеть на знаменитой Эшеровской гравюре «Метаморфоза»(рис. 8). Она немного напоминает «Естественно Растущий Канон»: уходя все дальше и дальше от начального пункта, мы внезапно возвращаемся обратно к началу. В черепичных плоскостях «Метаморфозы» уже есть намек на бесконечность; однако другие картины Эшера являют еще более смелые образы бесконечного, На некоторых его рисунках одна и та же тема «звучит» на нескольких уровнях реальности. Скажем, один из планов легко узнается как фантастический, в то время как другой представляет реальность. Сама картина, возможно, содержит только эти два плана; однако само наличие подобной «двусмысленности» приглашает зрителя увидеть самого себя как часть еще одного плана. Сделав этот шаг, он уже околдован предложенной Эшером возможностью бесконечной последовательности планов, где для каждого данного уровня существует высший, более «реальный», и низший, более «фантастичный» уровни. Такая ситуация сама по себе является достаточно удивительной и пугающей. Однако что произойдет, если цепь уровней к тому же будет не линейная, а замкнутая саму на себя, образуя Петлю? Что тогда будет реальностью, а что фантазией? Гений Эшера заключается в том, что он не только придумал, но и сумел изобразить десятки полуреальных, полумифических миров, миров, полных Странных Петель, куда он приглашает войти Зрителя.

Гёдель

Рис. 9. Курт Гёдель

Во всех примерах Странных Петель, которые мы видели у Баха и Эшера, присутствует конфликт между конечным и бесконечным, конфликт, рождающий ощущение парадокса. Интуиция подсказывает, что здесь замешано нечто, связанное с математикой. В самом деле, не так давно — в нашем веке — было найдено математическое соответствие этого явления. Это открытие оказало огромное влияние на развитие логической мысли. Подобно Петлям Баха и Эшера, основанным на простых и привычных образах (музыкальная гамма, лестница), открытие Странных Петель в математических системах, принадлежащее К. Гёделю, берет свое начало в простых и интуитивных идеях. В самой упрощенной форме открытие Гёделя сводится к переводу на язык математики одного из старинных философских парадоксов, так называемого парадокса Эпименида (или парадокса лжеца). Критский философ Эпименид был автором бессмертного суждения: «Все критяне — лжецы». В более прямой форме парадокс звучит так: «Я лгу» или «Это высказывание — ложь». В дальнейшем, говоря о парадоксе Эпименида, я буду иметь в виду последний вариант. Это суждение грубо нарушает обычное представление о том, что все суждения делятся на истинные и ложные, так как если мы на минуту представим, что оно истинно, то тут же увидим, что мы ошиблись, и на самом деле суждение ложно. Точно так же, из предпосылки ложности этого суждения вытекает, что оно должно быть истинным, Попробуйте сами!

Парадокс Эпименида является Странной Петлей «в одну ступеньку», так же, как «Картинная галерея» Эшера. Но какое отношение имеет он к математике? В этом как раз и заключается открытие, сделанное Гёделем. Он попытался использовать математические рассуждения для анализа самих же математических рассуждений. Идея заставить математику заняться «самоанализом» оказалась необычайно продуктивной; теорема Гёделя о неполноте, пожалуй, самое важное её следствие. То, что эта теорема утверждает, и то, как это утверждение в ней доказывается, это разные вещи, которые мы подробно рассмотрим в дальнейшем. Саму теорему можно сравнить с жемчужиной, а метод доказательства — с устрицей, её скрывающей. Мы восхищаемся сияющей простотой жемчужины; устрица же является сложным живым организмом, в чьем нутре зарождается эта таинственно простая драгоценность.

Теорема Гёделя впервые увидела свет как «теорема VI» в его статье 1931 года «О формально неразрешимых суждениях в „Principia Mathematica“ и родственных системах, I». Теорема утверждает следующее:

Каждому ω-непротиворечивому рекурсивному классу формул k соответствует рекурсивный символ классов r такой, что ни v Gen r ни Neg (v Gen r) не принадлежат к Flg (к), где v - свободная переменная r.

В оригинале это было написано по-немецки; читатель, возможно, думает, что с тем же успехом можно было бы это на немецком и оставить. Постараемся привести перевод на более понятный язык.

Все непротиворечивые аксиоматические формулировки теории чисел содержат неразрешимые суждения.

Это наша жемчужина.

В ней трудно увидеть Странную Петлю, потому что эта Петля спрятана в «устрице» — в доказательстве. Доказательство теоремы Гёделя о неполноте вращается вокруг автореферентного (описывающего самого себя) математического суждения, так же как парадокс Эпименида — вокруг такого суждения в языке. Говорить о языке, используя для этого сам язык, несложно; гораздо труднее вообразить, как может говорить само о себе математическое суждение о числах. На самом деле, уже для того, чтобы связать идею автореферентного суждения с теорией чисел, понадобился гениальный ум. Интуитивно придя к мысли о возможности такого суждения, Гёдель преодолел одну из основных трудностей. Само же создание автореферентного суждения было делом техники, раздуванием костра из блистательной искры мгновенного прозрения.

Мы остановимся на теореме Гёделя в последующих главах; но чтобы покуда не оставить читателя в полной тьме, я несколькими штрихами обрисую суть идеи в надежде на то, что это заставит вас задуматься. Для начала уясним, в чем здесь основная трудность. Математические суждения описывают свойства целых чисел (мы будем говорить здесь о суждениях теории чисел). Ни целые числа, ни их свойства не являются сами по себе суждениями. Суждения теории чисел не говорят ничего про суждения теории чисел; они не более как суждения теории чисел. В этом и заключается проблема; однако Гёдель сумел увидеть глубже того, что лежит на поверхности.

Гёдель предположил, что суждение теории чисел могло бы быть о суждении теории чисел (возможно даже о себе самом), если бы сами числа могли обозначать суждения. Иными словами, в центре его построения находится идея кода. В этом коде, обычно именуемом «Гёделевой нумерацией», символы и последовательности символов обозначаются числами. Таким образом, любое суждение теории чисел, будучи последовательностью специальных символов, получает Гёделев номер, что-то вроде телефонного номера или номерного знака машины. В дальнейшем, для ссылки на данное суждение используется соответствующий Гёделев номер. С помощью этого кодирующего трюка суждения теории чисел приобретают двоякое значение: они могут быть поняты как суждения теории чисел, а так же как суждения о суждениях теории чисел.

После того, как Гёдель изобрел эту кодирующую схему, ему пришлось разработать в деталях способ перевода парадокса Эпименида на формальный язык теории чисел. Конечный результат «пересадки» Эпименида на формальную почву звучит так: «Это суждение теории чисел не имеет доказательства» (вместо «Это суждение теории чисел ложно»). Эта формулировка может создать немалую путаницу. так как «доказательство» для многих является весьма приблизительным понятием. В действительности, труды Геделя были лишь частью долгих поисков, предпринятых математиками в надежде выяснить, что же такое доказательства. Необходимо помнить тот факт, что доказательства являются таковыми только внутри жестких систем теорем. В Гёделевской работе такой жесткой системой, к которой относится слово «доказательство», является огромный труд Бертрана Рассела и Альфреда Норта Уайтхеда «Principia Mathematical» («Основания математики»), опубликованный между 1910 и 1913 годами. Следовательно, Гёделево высказывание Г должно бы звучать более правильно как:

Это суждение теории чисел не имеет доказательств в системе «Оснований математики».

Заметим, между прочим, что Гёделево высказывание Г само по себе не является теоремой Гёделя, так же как высказывание Эпименида не является замечанием «Высказывание Эпименида — парадокс». Теперь мы можем установить, какой эффект произвело открытие Г. В то время как высказывание Эпименида создает парадокс, потому что оно не является ни истинным, ни ложным, Гёделево высказывание Г — истинно, хотя и не доказуемо в системе «Оснований математики». Из этого следует замечательный вывод: система «Оснований математики» неполна, так как существуют истинные суждения теории чисел, не доказуемые методами самой теории (эти методы доказательства оказываются слишком «слабыми».)

«Основания математики» явились первой, но далеко не последней жертвой удара. Выражение «и родственные системы» в заглавии Гёделевой статьи говорит о многом. Если бы результат, полученный Гёделем, указывал бы только на дефект в работе Рассела и Уайтхеда, другие математики могли бы попытаться исправить ошибки в «Основаниях математики» и «перехитрить» теорему Гёделя. Однако это оказалось невозможным: теорема Гёделя была приложима ко всем аксиоматическим системам, ставившим своей целью то же, что и система Рассела и Уайтхеда. Для различных систем подходил один и тот же основной трюк. Короче, Гёдель показал, что понятие «доказуемости» уже, слабее понятия истинности вне зависимости от того, какую аксиоматическую систему мы выбираем.

Таким образом, теорема Гёделя произвела электризующий эффект на логиков, математиков и философов, заинтересованных в основах математики, поскольку она показала, что ни одна установленная система, какой бы сложной она не была, не может отразить всей сложности целых чисел: 0,1, 2, 3… Современный читатель, возможно, не окажется от этого в таком замешательстве, как читатели 1931 года, так как за прошедшее время наша культура впитала теорему Гёделя вместе с революционными идеями теории относительности и квантовой механики, и широкая публика получила доступ к этим концепциям, поражающим и дезориентирующим мышление даже в смягченном прослойкой переводов (а зачастую и затемненном этими переводами) виде. Сейчас идея «ограничивающих» результатов витает в воздухе; тогда, в 1931 году, она была как гром с ясного неба.

Математическая логика: краткий обзор

Чтобы полностью оценить теорему Гёделя, необходим определенный контекст. Я попытаюсь здесь дать обзор истории математической логики до 1931 года на нескольких страницах — невозможная задача! (Хорошее изложение истории этого предмета читатель может найти у Делонга, Нибоуна, или Нагеля и Ньюмена). Все началось с попытки механизировать мыслительный процесс логических рассуждений. Обратите внимание, что умение мыслить всегда рассматривалось как отличительная черта человека; на первый взгляд, желание механизировать самую человеческую черту кажется парадоксальным. Тем не менее, уже древние греки знали, что логическое мышление - структурный процесс, до некоторой степени управляемый определенными законами. Эти законы можно описать. Аристотель систематизировал силлогизмы, а Эвклид — геометрию; однако с тех пор прошло много веков до того, как в изучении логического мышления снова наступила эра прогресса.

Одним из важнейших открытий геометров девятнадцатого столетия были различные геометрии, равно имеющие право на существование. Под геометрией здесь понимается теория, описывающая свойства абстрактных точек и линий. До этого считалось, что геометрия — это система, кодифицированная Эвклидом; она могла иметь незначительные недостатки, которые могли быть со временем исправлены. Таким образом, любой прогресс в этой области означал исправление и дополнение Эвклида. Это убеждение было разбито вдребезги, когда несколько математиков почти одновременно открыли неэвклидову геометрию — открытие, потрясшее математический мир, поскольку оно сильно поколебало бытовавшее мнение, что математика изучает реальную действительность. Каким образом в одной и той же реальности могли существовать различные типы точек и линий? Сегодня решение этой дилеммы может быть очевидно даже для некоторых далеких от математики людей, но в то время она посеяла панику в математических кругах.

Позже в девятнадцатом веке английские логики Джордж Буль и Август де Морган пошли значительно дальше Аристотеля в кодификации строго дедуктивных рассуждений. Буль даже назвал свою книгу «Законы мысли», что, безусловно, было некоторым преувеличением; однако его попытки внесли серьезный вклад в общие усилия. Льюис Кэрролл был очарован механическими методами рассуждений и изобрел множество головоломок, решавшихся с помощью этих методов. Готтлоб Фреге в Йене и Джузеппе Пеано в Турине работали над соединением формальных рассуждений с изучением чисел и множеств. Дэвид Гильберт в Геттингене трудился над более строгой, чем у Эвклида, формализацией геометрии. Все эти усилия были направлены на выяснение вопроса о том, что же такое «доказательство».

Между тем, в классической математике тоже происходили интересные события. В 1880-х годах Георг Кантор развил теорию о различных типах бесконечности, известную под именем теории множеств. Теория Кантора была глубока и красива, но шла вразрез с интуицией; вскоре на свет появилось целое семейство парадоксов, основанных на теории множеств. Ситуация была не из приятных. Только математики начали оправляться от удара, нанесенного по математическому анализу парадоксами, связанными с теорией пределов, как попали из огня в полымя из-за нового, еще худшего набора парадоксов!

Самый известный из них — парадокс Рассела. По всей видимости, большинство множеств не являются элементами самих себя: скажем, множество моржей — это не морж; множество, содержащее только одного члена, Жанну д'Арк, само не является Жанной (множество не человек!), и так далее. В этом смысле, большинство множеств совершенно заурядны. Однако существуют такие «самозаглатывающие» множества, которые содержат самих себя, как, например, множество всех множеств, или множество всех вещей за исключением Жанны Д'Арк, и тому подобные. Ясно, что множества могут быть только одного из этих двух типов — либо заурядные, либо самозаглатывающие — и ни одно множество не может входить сразу в два класса. Однако ничто не мешает нам изобрести множество R всех заурядных множеств. На первый взгляд, R кажется довольно заурядным изобретением, но вам придется пересмотреть свое мнение, если вы спросите себя, является ли множество R самозаглатывающим или заурядным. Вы придете к следующему ответу: R не является ни тем, ни другим, так как любой из этих двух ответов приводит к парадоксу. Попробуйте и убедитесь сами!

Но если R не заурядное и не самозаглатывающее, тогда что же оно такое? По меньшей мере, ненормальное. Однако такой уклончивый ответ никого не удовлетворял. Тогда люди стали пытаться докопаться до основ теории множеств; при этом они задавали себе следующие вопросы: «В чем заключается ошибка нашего интуитивного понимания понятия „множество“? Можно ли создать строгую теорию множеств, которая бы не противоречила нашей интуиции и в то же время исключала бы парадоксы?» Здесь, так же как и в теории чисел и в геометрии, проблема заключалась в том, чтобы примирить интуицию с формальными, аксиоматическими системами логических рассуждений.

Удивительный вариант парадокса Рассела, называющийся парадоксом Греллинга, получается, если вместо множеств использовать прилагательные. Разделите все прилагательные русского языка на две категории: те, которые описывают самих себя, «самоописывающие», («пятисложное», «шелестящий,» «пренеестественнейший» и т. п.), и те, которые таким свойством не обладают («съедобный», «двусложный», «кратчайший»). Рассмотрим теперь прилагательное «несамоописывающий». К какому классу оно относится? Попробуйте ответить!

У всех этих парадоксов есть общий виновник: автореферентность, или «страннопетельность». Таким образом, если наша цель — избавиться от всех парадоксов, то почему бы нам не попытаться избавиться от автореферентности и тех условий, которые ее порождают? Это не так легко, как кажется, так как иногда бывает трудно найти, где именно происходит автореференция. Иногда она бывает распределена по Странной Петле в несколько ступеней, как в следующей расширенной версии парадокса Эпименида, напоминающей Эшеровские «Рисующие руки» —

Следующее высказывание ложно.

Предыдущее высказывание истинно.

Вместе эти высказывания производят такой же эффект, как первоначальный парадокс Эпименида; однако взятые по отдельности они безобидны и даже полезны Ни одно из них не может нести ответственности за Странную Петлю; виновато их объединение, то, как они указывают друг на друга. Точно так же каждый взятый по отдельности кусок «Подъема и спуска» совершенно правилен; невозможно лишь подобное соединение этих кусков в одно целое Видимо, существуют прямой и косвенный типы автореферентности; если мы считаем, что в автореферентности — корень зла, то мы должны найти способ избавиться сразу от обоих типов.

Изгнание Странных Петель

Рассел и Уайтхед считали именно таких труд «Основания математики» («ОМ») был титаническим усилием, направленным на изгнание Странных Петель из логики, теории множеств и теории чисел. В основе их системы лежала следующая идея. Множество «низшего» типа могло иметь своими элементами лишь «предметы», а не множества. На следующей ступени стояли множества, которые могли содержать предметы или множества первого типа. Вообще, любое данное множество могло содержать лишь множества низшего типа или предметы. Каждое множество принадлежало к определенному типу. Ясно, что никакое множество не могло содержать самого себя, так как оно оказалось бы тогда принадлежащим к более высокому типу, чем его собственный. В такой системе существуют лишь обыкновенные множества; более того, наш старый знакомец, множество R, теперь вообще не считается множеством, так как оно не принадлежит ни к одному конечному типу! По всей видимости, эта теория типов, которую мы также могли бы именовать «теорией уничтожения Странных Петель», преуспела в избавлении теории множеств от парадоксов — но только ценой введения искусственной иерархии и запрета на определенный тип множеств, такой, например, как множество всех «заурядных» множеств. Интуитивно это идет вразрез с нашим представлением о множествах.

Теория типов справилась с парадоксом Рассела, но ничего не предприняла в отношении парадоксов Эпименида или Греллинга. Для тех, чей интерес не шел дальше теории множеств, этого было достаточно; однако людям, заинтересованным в уничтожении парадоксов вообще, казалось необходимым создание подобной иерархии в языке, чтобы изгнать оттуда Странные Петли. На первой ступеньке такой иерархии стоял бы предметный язык, на котором возможно говорить лишь об определенной сфере предметов, но нельзя говорить о самом предметном языке, обсуждать его грамматику или какие-либо высказывания, для этого понадобился бы метаязык. (Опыт двух различных лингвистических уровней знаком любому, кто изучал иностранные языки.) В свою очередь, чтобы говорить о метаязыке, потребовался бы метаметаязык, и так далее. Каждое высказывание должно было принадлежать к определенному уровню иерархии. Таким образом, если бы мы не могли найти для данного высказывания места в иерархической структуре, мы должны были бы считать такое высказывание бессмысленным и как можно скорее выбросить его из головы.

Можно попытаться проанализировать таким образом двуступенчатую петлю Эпименида, приведенную выше. Первое высказывание, поскольку оно говорит о втором, должно быть уровнем выше последнего; однако точно такое же рассуждение применимо и ко второму высказыванию. Поскольку это невозможно, оба высказывания «бессмысленны». Точнее, они вообще не могут существовать в системе, основанной на строгой иерархии языков. Это предупреждает возникновение любых версий парадокса Эпименида или Греллинга (К какому уровню принадлежит «самоописывающий»?)

В теории множеств, имеющей дело с абстракциями, далекими от повседневной жизни стратификация теории типов еще приемлема, хотя и выглядит натянутой. Когда же дело доходит до языка, важнейшей и ежедневно употребляемой части нашей жизни, такая стратификация кажется абсурдом. Трудно поверить что, разговаривая, мы скачем вверх и вниз по иерархии языков. Довольно обычное высказывание, такое как, например, «В этой книге я критикую теорию типов», было бы дважды запрещено в подобной системе. Во-первых, оно упоминает «эту книгу», которая должна бы упоминаться только в «метакниге», и во-вторых, оно упоминает обо мне — существе, о котором я не должен бы говорить вообще. Этот пример показывает, насколько нелепо выглядит теория типов в повседневном контексте. В данном случае, лекарство хуже самой болезни метод, используемый этой теорией, чтобы избавиться от парадоксов, заодно объявляет бессмыслицей множество вполне правильных конструкций. Эпитет «бессмысленный» кстати, был бы приложим к любому обсуждению теории лингвистических типов (и в частности, к данному параграфу), так как ясно, что никакое из них не может принадлежать ни к одному из уровней — ни к предметному ни к метаязыку, ни к метаметаязыку, и т. д. Таким образом, сам акт обсуждения теории оказывался бы ее грубейшим нарушением.

Конечно, мы могли бы попытаться защитить подобные теории, обговорив, что они имеют дело только с формальными языками, а не с повседневным, обыкновенным языком. Может, оно и так, но тогда такие теории оказываются чисто академическими и имеют дело с парадоксами только тогда, когда те возникают в специальных сделанных по заказу системах. К тому же, стремление уничтожить парадоксы любой ценой, особенно ценой создания чрезвычайно искусственных формализмов, придает слишком много значения плоской последовательности и логичности, и слишком мало — тому причудливому и замысловатому, что придает вкус жизни и математике. Вне сомнения, стараться быть последовательным важно, но когда это старание приводит к созданию удивительно неуклюжих и уродливых теорий, становится ясно, что здесь что-то не в порядке.

В начале двадцатого века, проблемы подобного типа в основах математики вызвали живой интерес к кодификации методов логического мышления. Математики и философы начали сомневаться в том, что даже самые конкретные теории, такие, как теория чисел, построены на прочном фундаменте. Если парадоксы могли возникнуть в теории множеств, основанной на простых интуитивных понятиях, то почему бы им не проникнуть и в другие области математики? А что, если логические парадоксы, такие как парадокс Эпименида, свойственны математике в целом, и, таким образом, ставят всю ее под сомнение? Подобные проблемы тревожили в первую очередь тех — а их было немало — кто твердо верил в то, что математика — лишь один из разделов логики (или, наоборот, что логика — лишь один из разделов математики). Уже сам этот вопрос, «являются ли математика и логика отдельными и непохожими дисциплинами?», вызывал горячие споры.

Изучение самой математики получило название метаматематики или, иногда, металогики, поскольку математика и логика тесно переплетены. Важнейшей задачей метаматематиков было определение природы математических рассуждений. Что является законным методом рассуждений и что — незаконным? Поскольку рассуждения велись на каком-либо «естественном языке», скажем, французском или латинском, всегда были возможны двусмысленные и неясные толкования. Одно и то же слово может иметь разные значения для разных людей, вызывать различные образы, и так далее. Хорошей и важной идеей казалось установление единой нотации, с помощью которой велись бы все математические рассуждения, так чтобы два математика всегда могли договориться о том, верно ли предложенное доказательство. Эта задача потребовала бы кодификации всех общепринятых методов человеческих рассуждений, по крайней мере постольку, поскольку они приложимы к математике.

Последовательность, полнота, и программа Гильберта

Такая кодификация являлась основной идеей системы «Оснований математики» («ОМ»), авторы которой задались целью вывести всю математику из логики, причем без малейших противоречий! Многие восхищались их грандиозным трудом, но никто не был уверен в том, что 1) методы Рассела и Уайтхеда действительно описывают всю математику и 2) эти методы достаточно последовательны и корректны. Действительно ли при следовании этим методам никогда и не при каких условиях не могло возникнуть парадоксов?

Этот вопрос особенно тревожил знаменитого немецкого математика (и метаматематика) Дэвида Гильберта, кто поставил перед математиками (и метаматематиками) всего мира следующую задачу: со всей строгостью доказать, возможно, при помощи самих методов Рассела и Уайтхеда, что эти методы, во-первых, непротиворечивы и во-вторых, полны (иными словами, что в системе «ОМ» может быть выведено любое истинное высказывание). Эта задача весьма непростая, и ее можно критиковать за некоторую «порочную кругообразность», как можно пытаться доказать какие-либо методы рассуждения, пользуясь этими же методами? Это все равно, что пытаться поднять самого себя на воздух за шнурки от собственных ботинок. (Кажется, нам-таки никуда не деться от этих Странных Петель)

Гильберт, разумеется, полностью отдавал себе отчет в этой дилемме; однако он надеялся, что доказательство полноты и непротиворечивости удастся найти с помощью только небольшой группы так называемых «финитных» методов рассуждения, признаваемых большинством математиков. В этом смысле Гильберт надеялся, что математикам все же удастся «поднять самих себя на воздух за шнурки ботинок», доказав правильность всех математических методов путем использования лишь нескольких из них. Эта цель может показаться слишком эзотерической, однако именно она занимала умы многих великих математиков в первые тридцать лет двадцатого столетия.

Однако в тридцать первом году Гёдель опубликовал работу, подорвавшую основы Гильбертовой программы. Эта работа показала не только наличие незаполнимых «дыр» в аксиоматической системе, предложенной Расселом и Уайтхедом, но и то, что ни одна аксиоматическая система не может породить все истинные высказывания теории чисел, если она не является противоречивой! Наконец, Гёдель показал, насколько тщетна надежда доказать непротиворечивость системы «ОМ» если бы такое доказательство было найдено только при помощи методов, используемых в «ОМ» — и это одно из самых удивительных следствий Гёделевской работы — сами «ОМ» оказались бы противоречивы!

Последний иронический штрих для доказательства теоремы Гёделя о неполноте потребовалось внедрить парадокс Эпименида прямо в сердце «Оснований математики» — бастиона, считавшегося недоступным для Странных Петель. Хотя Гёделева Странная Петля и не разрушила «Оснований математики», она сделала их гораздо менее интересными для математиков, доказав иллюзорность цели, первоначально поставленной Расселом и Уайтхедом.

Баббидж, компьютеры, искусственный разум...

Как раз когда работа Гёделя вышла в свет, мир был накануне создания электронных цифровых компьютеров. Идея механических счетных машин носилась в воздухе уже давно В семнадцатом веке Паскаль и Лейбниц разработали машины для выполнения установленных операций сложения и умножения. К сожалению, эти машины не имели памяти и не были, в современном понимании этого слова, программируемыми

Первым человеком, понявшим, какой огромный счетный потенциал заключают в себе машины, был лондонец Чарльз Баббадж (Charles Babbage, 1792- 1871), фигура, словно сошедшая со страниц «Пиквикского клуба». При жизни он был известен более всего тем, что вел энергичные кампании по очистке Лондона от «нарушителей спокойствия», в первую очередь, шарманщиков.

Эти паразиты любили подразнить Баббаджа и исполняли для него «серенады» в любой час дня и ночи, а он, в ярости, гнал их вдоль по улице. Сегодня мы признаем, что Баббадж был человеком, обогнавшим свое время лет на сто он не только изобрел основные принципы современных компьютеров, но и был первым борцом за охрану окружающей среды от шума.

Его первое изобретение, «разностная машина», могла вычислять математические таблицы многих типов по «методу разностей». Однако, прежде чем была создана первая модель «РМ», Баббаджем завладела идея гораздо более революционная его «аналитическая машина». Довольно нескромно, Баббадж писал: «Я пришел к этой мысли таким сложным и запутанным путем, какой, возможно, впервые прошел человеческий ум». В отличие от созданных ранее машин, «AM» должна была иметь «склад» (память) и «фабрику» (считающее и принимающее решения устройство). Оба устройства должны были быть построены из тысяч цилиндров, сцепленных самым сложным и причудливым образом. Баббадж представлял себе числа, влетающие и вылетающие из «фабрики» под контролем некоторой программы, содержащейся в перфорированных картах — на эту идею его натолкнул ткацкий станок Жаккара, изготовлявший при помощи подобных карт удивительно сложные узоры. Подруга Баббаджа графиня Ада Лавлейс, дочь Байрона, женщина незаурядного таланта и горькой судьбы, поэтично прокомментировала: «Аналитическая машина ткет алгебраические узоры, наподобие того, как станок Жаккара ткет узоры из цветов и листьев». К сожалению, использование графиней настоящего времени вводит читателя в заблуждение: «AM» так никогда и не была построена, и Баббадж умер горько разочаровавшимся человеком.

Леди Лавлейс не менее, чем Баббадж, отдавала себе отчет в том, что, пытаясь создать аналитические машины, человечество флиртовало с искусственным разумом — в особенности, если эти машины способны «укусить себя за хвост» (так Баббадж описывал Странную Петлю, получавшуюся, когда его машина «залезала внутрь себя» и меняла заложенную в нее программу). В 1842 году она написала в своих мемуарах, что аналитическая машина «может воздействовать не только на цифры, но и на другие вещи». В то время, как Баббадж мечтал о создании шахматного или «крестико-ноликового» автомата, леди Лавлейс предположила, что если записать на цилиндры машины тона и гармонии, то она могла бы «создавать искусно сделанные научные музыкальные композиции любой сложности и длины». Впрочем, там же она объясняет: «Аналитическая машина не претендует на создание чего-то нового, она может делать только то, что мы умеем ей приказать». Верно поняв, какая мощь заложена в механических вычислениях, она, тем не менее, оставалась скептически настроенной по отношению к механическому разуму. Однако могла ли она, со всей своей проницательностью, предположить, какие возможности откроются, когда человечество подчинит себе электричество?

В нашем веке пришло время для компьютеров, превзошедших самые смелые мечты Паскаля, Лейбница, Баббаджа или леди Лавлейс. В 1930-х и 1940-х годах были разработаны и построены первые «блестящие электронные головы». Это послужило катализатором к соединению трех ранее совершенно различных областей науки, теории аксиоматических рассуждений, изучения механических вычислений и исследований по психологии человеческого разума. В те же годы гигантскими скачками двигалась вперед теория компьютеров. Эта теория была тесно связана с математикой. Фактически, теорема Гёделя имеет параллель в теории вычислений: Алан Тюринг открыл существование неизбежных «дыр» в возможностях даже самого могучего компьютера. Словно в насмешку, как раз когда делались эти довольно мрачные прогнозы, строились новые компьютеры, чьи возможности росли на глазах, далеко превосходя самые смелые предсказания их создателей. Баббадж, сказавший однажды, что он с радостью отдал бы остаток жизни за возможность вернуться на три дня лет через пятьсот, чтобы получить возможность ознакомиться с наукой будущего, возможно, потерял бы дар речи от удивления уже через сто лет после своей смерти, пораженный как новыми машинами, так и их неожиданными ограничениями.

В начале 1950-х годов казалось, что до механического разума — рукой подать: однако за каждой преодоленной вершиной вставала новая, препятствуя созданию по-настоящему думающей машины. Возможно ли, что это упорное отдаление цели имело глубинные причины?

Никто не знает, где пролегает граница между разумным и не-разумным поведением; в самом деле, возможно, что само предположение о существовании четкой границы звучит глупо. Однако мы с уверенностью можем перечислить основные критерии разума:

гибко реагировать на различные ситуации;

извлекать преимущество из благоприятного стечения обстоятельств;

толковать двусмысленные или противоречивые сообщения;

оценивать различные элементы данной ситуации по степени их важности;

находить сходство между ситуациями, несмотря на возможные различия;

находить разницу между ситуациями, несмотря на возможное сходство;

создавать новые понятия, по-новому соединяя старые;

выдвигать новые идеи.

Здесь мы сталкиваемся с кажущимся парадоксом. Компьютеры, по определению, являются самыми негибкими, безвольными и послушными приказам существами. Несмотря на свою быстроту, они, тем не менее, сама бессознательность. Как же, в таком случае, можно запрограммировать разумное поведение? Не является ли уже само это предположение кричащим противоречием? Одна из основных идей этой книги — показать, что это вовсе не противоречие. Одна из основных целей этой книги — побудить каждого читателя встретиться с кажущимся парадоксом во всеоружии, попробовать его на вкус, вывернуть его наизнанку, разобрать его на части, пошлепать в нем, как ребенок в луже, чтобы в результате читатель смог взглянуть по-новому на кажущуюся неприступной пропасть между формальным и неформальным, одушевленным и неодушевленным, гибким и негибким

Это и составляет предмет исследований науки об искусственном интеллекте (ИИ). Работа специалистов по ИИ кажется странной и удивительной именно потому, что они разрабатывают строго формальные правила, говорящие негибким машинам, как стать гибкими

Что же это за правила такие, могущие описать всю сложность поведения разумных существ? Безусловно, это должны быть правила самых разных уровней: «простые» правила, «метаправила» для модификации «простых», «метаметаправила» для модификации метаправил, и так далее. Гибкость нашего разума зависит именно от огромного количества правил и сложности их иерархии. Некоторые ситуации вызывают стереотипные реакции, для которых годятся «простые» правила. Другие ситуации представляют собой комбинации из стереотипных ситуаций; тут нужны правила, говорящие, какие из «простых» правил приложимы к данной ситуации. Некоторые ситуации вообще не поддаются классификации — следовательно, требуются правила для изобретения новых правил… ит. д., и т. п. Без сомнения, Странные Петли, правила, изменяющие сами себя, находятся в самом сердце разума. Иногда сложность нашего разума кажется нам настолько поразительной, что у нас опускаются руки перед задачей понять и описать его; тогда нам кажется, что никакие, даже самые замысловатые иерархические правила не способны управлять поведением разумных существ.

...и Бах

В 1754 году, четыре года спустя после смерти И. С. Баха, лейпцигский теолог Иоганн Микаэль Шмидт написал в своем труде о музыке и о душе следующие достойные внимания строки:

Не так давно из Франции сообщили, что там сделана была статуя, способная исполнить несколько пьес на Fleuttraversiere; статуя эта подносит флейту к губам и затем ее опускает, двигает глазами и т. д. Однако никто еще не изобрел образа, который бы думал, желал, сочинял или делал бы что-либо отдаленно подобное. Пусть любой, кто желает в этом убедиться, обратится к последним фугам Баха, которому мы уже воздали почести ранее. (Эти фуги были выгравированы на меди, но не были закончены, так как этому помешала слепота композитора.) Пусть увидит наблюдатель, какое искусство содержится в этой музыке — еще более он будет поражен чудесным Хоралом, который был записан под диктовку слепого Баха. «Wenn wir in hőchen Nothen seyn». Я уверен, что наблюдателю вскоре понадобится душа, ежели он желает прочувствовать всю содержащуюся в этой музыке красоту или, более того, исполнить эту музыку и составить суждение об авторе. Все аргументы чемпионов Материализма должны рассыпаться в прах лишь от одного этого примера.

Скорее всего, под главным «чемпионом Материализма» здесь имеется в виду не кто иной как Жюльен Оффрой де Ламеттри, придворный философ Фридриха Великого, автор книги «Человек как машина» и материалист до мозга костей. С тех пор прошло более двухсот лет, но битва между сторонниками Иоганна Микаэля Шмидта и Жюльена Оффроя де Ламеттри все еще в полном разгаре. В этой книге я надеюсь дать читателю некоторую перспективу этой битвы.

«Гёдель, Эшер, Бах»

Эта книга построена необычно — как контрапункт между Диалогами и Главами. С помощью такой структуры я смог вводить новые понятия дважды: каждое из них сначала представлено в метафорической форме в диалоге, что дает читателю конкретные зрительные образы; эти образы затем служат интуитивным фоном для более серьезного, абстрактного обсуждения того же понятия. Многие Диалоги создают поверхностное впечатление, что я говорю о какой-то определенной идее, когда на самом деле я имею в виду совсем иную идею, тщательно замаскированную.

Сначала единственными действующими лицами моих Диалогов были Ахилл и Черепаха, пришедшие ко мне от Зенона из Элей через посредство Льюиса Кэрролла. Зенон, изобретатель парадоксов, жил в 5 веке до н.э. Один из его парадоксов был аллегорией, в которой действовали Ахилл и Черепаха. История изобретения Зеноном этой счастливой парочки рассказана в первом Диалоге, «Трехголосная инвенция». В 1895 году Льюис Кэрролл воссоздал Ахилла и Черепаху для иллюстрации своего собственного нового парадокса о бесконечности. Парадокс Кэрролла, заслуживающий гораздо большей популярности, играет значительную роль в этой книге. В оригинале он называется «Что Черепаха сказала Ахиллу» — здесь он приведен как «Двухголосная инвенция».

Вскоре после того, как я начал писать Диалоги, каким-то образом они связались в моим воображении с музыкальными формами. Не помню того момента, когда это произошло, помню лишь, как однажды я в задумчивости написал «фуга» над текстом одного из ранних Диалогов. Идея привилась, и с тех пор я стал писать Диалоги, формально составленные по образцу различных композиций Баха. Это оказалось неплохой мыслью. Сам Бах часто напоминал своим ученикам, что различные части их композиций должны вести себя как «люди, беседующие друг с другом в избранном обществе». Возможно, что я вложил в этот совет более буквальный смысл, чем Бах, надеюсь все же, что результат оказался верен также и его духу. Особенно меня вдохновили некоторые поразительные аспекты Баховских композиций, которые так прекрасно описаны Менделем и Давидом в их книге «Баховская хрестоматия» (Mendel & David, «The Bach Reader»):

Форма у Баха в основном опиралась на соотношения между отдельными частями от полного сходства с одной стороны до повторения какого-либо одного композиционного принципа или просто мелодической переклички с другой стороны. Получившиеся композиции часто бывали симметричными но это никоим образом не являлось необходимым следствием. Иногда соотношения между частями создают запутанный клубок, который можно распутать только путем детального анализа. Обычно впрочем, несколько доминирующих черт позволяют сориентироваться с первого взгляда или прослушивания, хотя при дальнейшем изучении мы можем открыть для себя множество тонкостей нас никогда не покидает чувство единства, связывающего каждое произведение Баха в одно гармоничное целое.

Я решил попытаться сплести Бесконечную Гирлянду из этих трех прядей Гедель, Эшер, Бах. По началу я планировал написать эссе, центральной темой которого была бы теорема Геделя о неполноте. Я думал, что у меня получится тоненькая брошюрка, однако мой проект стал расти, как снежный ком, и вскоре затронул Баха и Эшера. Некоторое время я не знал, выразить ли эту связь открыто или же оставить ее при себе как источник собственного вдохновения. В конце концов я понял, что Гедель, Эшер и Бах для меня — только тени, отбрасываемые в разные стороны некой единой центральной сущностью. Я попробовал реконструировать этот центральный объект, результатом моей попытки явилась эта книга.

Назад: ЧАСТЬ I

Дальше: Трехголосная инвенция