ГЛАВА XV: Прыжок из системы

Дальше: Благочестивые размышления курильщика табака

Более мощная формальная система

РАЗМЫШЛЯЯ над доказательством Гёделя, вдумчивый критик мог бы задаться вопросом, насколько оно обще. Он мог бы подумать, что Гёделю удалось найти недостаток лишь в одной формальной системе — в ТТЧ. Если бы это было так, то, возможно, удалось бы найти какую-нибудь лучшую систему, в которой Гёделев трюк был бы невозможен — и, таким образом, Теорема Гёделя потеряла бы значительную часть своей мощи. В этой главе мы подробно рассмотрим те характеристики ТТЧ, которые сделали ее уязвимой для аргументов, изложенных ранее.

Естественно подумать, что если проблема в том, что в ТТЧ есть «дырка» — иными словами, неразрешимое суждение G — то почему бы нам не заткнуть эту дырку? Почему бы не добавить G к ТТЧ в качестве шестой аксиомы? Конечно, по сравнению с остальными аксиомами, G — неуклюжий великан, и получившаяся система ТТЧ + G выглядела бы довольно комично из-за диспропорции ее аксиом. Тем не менее, это предложение имеет смысл. Представим себе, что перед нами ТТЧ + G — высшая формальная система. Мы надеемся, что она не только свободна от супернатуральных чисел, но и полна. Безусловно то, что ТТЧ + G лучше ТТЧ по крайней мере в одном, строчка G больше не является в ней неразрешимой, поскольку теперь она превратилась в теорему.

В чем же была причина недостатков ТТЧ? Ее уязвимость объяснялась тем, что она была способна говорить о себе самой. В частности, источником неприятностей было высказывание:

«Я не могу быть доказано в формальной системе ТТЧ»

или, более подробно,

«Не существует такого натурального числа, которое составляло бы пару доказательства ТТЧ с Гёделевым номером этой строчки.»

Есть ли у нас причина ожидать, что ТТЧ + G будет неуязвима для Гёделева доказательства? На самом деле, нет. Наша новая система может выразить ничуть не меньше, чем ТТЧ. Поскольку Гёделево доказательство основывается, прежде всего, на выразительной мощи формальной системы, будет неудивительно, если наша новая система окажется подверженной тому же недугу, как и ТТЧ. Для этого нужно будет найти строчку, выражающую высказывание:

«Я не могу быть доказано в формальной системе ТТЧ + G»

После того, как мы проделали подобное в ТТЧ, это совсем несложно. Принципы здесь те же самые, только контекст слегка изменен (Образно говоря, это все равно, что пропеть известную нам мелодию тоном выше.) Как и раньше, нужная нам строчка — назовем ее G' — строится при посредстве «дяди». Но теперь, вместо пары доказательства ТТЧ, она основывается на похожем, но немного более сложном понятии пары доказательства ТТЧ + G. Понятие пар доказательства ТТЧ + G — всего лишь небольшое расширение понятия пар доказательства ТТЧ.

Можно представить себе подобное расширение для системы MIU. Мы имели дело с неизмененной формой пар доказательства MIU. Если бы мы теперь добавили MU в качестве второй аксиомы, у нас получилась бы новая система — MIU + MU. Деривация в такой расширенной системе выглядела бы так:

MU аксиома

MUU правило 2

Существует пара доказательства MIU + MU, соответствующая этой деривации: m = ЗОЗОО, n = 300. Разумеется, эта пара чисел не является парой доказательства MIU, а всего лишь парой доказательства MIU + MU. Добавление дополнительной аксиомы ненамного усложнило арифметические свойства пар доказательства. Самое главное их свойство, примитивно-рекурсивность, сохраняется и в новой системе.

Метод Гёделя используется еще раз

Вернувшись к ТТЧ, мы находим похожую ситуацию. Пары доказательства ТТЧ + G, как и их предшественницы, примитивно рекурсивны. Они представимы в ТТЧ + G с помощью формулы, которую мы сократим следующим очевидным образом:

ПАРА-ДОКАЗАТЕЛЬСТВА-(ТТЧ + G){a,a'}

Теперь мы должны повторить знакомую процедуру. Чтобы сконструировать строчку, соответствующую G, начнем снова с «дяди»:

~Eа:Eа':<ПАРА-ДОКАЗАТЕЛЬСТВА-(ТТЧ + G){a,a'}

ΛARITHMOQUINE {а'',а'}>

Предположим, что Гёделев номер этой строчки — d'. Теперь мы арифмоквайнируем самого дядю. Это даст нам G':

~Eа:Eа':<ПАРА-ДОКАЗАТЕЛЬСТВА-(ТТЧ + G){a,a'}

ΛARITHMOQUINE {SSS.... SSSO/a'',a'}>

. |______|

. S повторяется d' раз

Интерпретация этой строчки такова:

«Меня нельзя доказать в формальной системе ТТЧ + G».

Разветвление

После этого остаются лишь технические детали. G' в ТТЧ + G — то же самое, чем G была в ТТЧ. Оказывается, что либо G, либо G' может быть добавлена к ТТЧ + G, и что результатом этого является дальнейшее разветвление теории чисел. Если вы думаете, что подобное происходит только с «положительными типами», то вы ошибаетесь: точно такой же трюк можно сыграть с ТТЧ + ~G, то есть, с нестандартным вариантом теории чисел, полученным путем добавления к ТТЧ отрицания G. Из рис. 75 видно, что у ТТЧ могут быть самые разные разветвления:

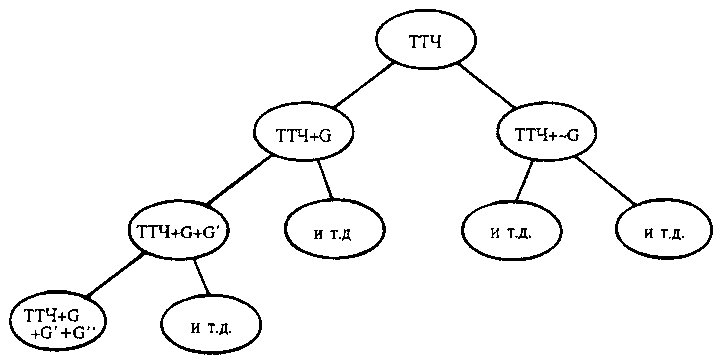
Рис. 75. Разветвление ТТЧ. У каждого нового варианта ТТЧ — своя Гёделева строчка; эта строчка или ее отрицание могут быть добавлены к системе, так что из каждой системы могут родиться два новых варианта; этот процесс может продолжаться до бесконечности.

Разумеется, это только начало. Представьте себе, что мы движемся вниз по самой левой ветви этого дерева, всегда добавляя саму Гёделеву строчку (а не ее отрицание). Это большее, что мы можем сделать, чтобы избавиться от супернатуральных чисел. После добавления G мы добавляем G'; затем G'', G''' и так далее. Каждый раз, когда мы производим новый вариант ТТЧ, ее уязвимость против Черепашьего метода — простите, я имею в виду Гёделева метода — позволяет вывести новую строчку, интерпретируемую как:

«Я не могу быть доказана в формальной системе X».

Разумеется, через некоторое время весь этот процесс начинает казаться привычным и легко предсказуемым — ведь все эти «дырки» делаются при помощи одной и той же техники! Это означает, что, как типографские объекты, они все сделаны по одному и тому же эталону — что, в свою очередь, означает, что они могут быть представлены с помощью одной-единственной схемы аксиом. Так почему бы нам не попытаться заткнуть все дырки одним махом, чтобы раз и навсегда избавиться от этой противной неполноты? Вместо того, чтобы добавлять по одной аксиоме, мы можем добавить к ТТЧ схему аксиом. Эта схема аксиом будет тем эталоном, по которому будут изготовляться G, G', G'', G''' и так далее. Может быть, что путем добавления этой схемы аксиом (назовем ее «G_ω.») нам удастся перехитрить метод «Гёделизации». Действительно, кажется совершенно ясным, что добавление G_ω, к ТТЧ будет последним шагом, необходимым для полной аксиоматизации всех истин теории чисел.

Этот момент соответствует тому месту «Акростиконтрапунктуса», где Черепаха рассказывает о создании Крабом патефона «Омега». Однако читатели были оставлены в неизвестности по поводу судьбы этого аппарата, поскольку усталая Черепаха решила поползти домой спать (но прежде, чем уйти, хитрое животное сделало тонкий намек на Теорему Гёделя о неполноте). Теперь, наконец, у нас дошли руки до того, чтобы прояснить ту ситуацию… Возможно, что, прочтя Диалог «Праздничная Кантататата», вы уже подозреваете, каков будет ответ.

Непополнимость

Как вы, наверное, и подозревали, даже это фантастическое улучшение ТТЧ не может избежать той же судьбы. Странно, что происходит это по той же причине, что и раньше. Схема аксиом недостаточно мощна, и к ней снова приложимо Гёделево построение. Постараюсь это объяснить. (Существует более строгое объяснение, чем то, которое я приведу здесь.) Если бы удалось описать все строчки G, G', G'', G''', … при помощи одной-единственной типографской схемы, это означало бы, что существует способ описать Гёделевы номера этих строчек при помощи одной-единственной арифметической схемы. И этот арифметический портрет бесконечного класса чисел может быть представлен в ТТЧ + G' при помощи некоей формулы АКСИОМА-ОМЕГА{а}, которая интерпретируется следующим образом: «а — это Гёделев номер одной из аксиом, получающихся из G_ω». Когда a заменяется на какой-либо определенный символ числа, получившаяся формула будет теоремой ТТЧ + G_ω тогда и только тогда, когда этот символ представляет собой Гёделев номер аксиомы, принадлежащей этой схеме.

С помощью этой новой формулы становится возможным представить даже такое сложное понятие как пара-доказательства-ТТЧ + G_ω внутри ТТЧ + G_ω:

ПАРА-ДОКАЗАТЕЛЬСТВА-(ТТЧ + G_ω){a,a'}

Используя эту формулу, мы можем построить нового «дядю» и затем приступить к его арифмоквайнированию уже знакомым нам способом, производя таким образом еще одну неразрешимую строчку, которую мы назовем «ТТЧ + G_ω+1». Вы, наверное, спросите, почему ТТЧ + G_ω+1 не находится среди аксиом, порожденных нашей схемой аксиом ТТЧ + G_ω? Ответом является то, что ТТЧ + G_ω оказалась недостаточно хитра, чтобы предусмотреть возможность своего собственного включения в теорию чисел.

В «Акростиконтрапунктусе» Черепаха, чтобы создать «непроигрываемую запись», должна была достать чертежи того патефона, который она собиралась разрушить. Это было необходимо для того, чтобы вычислить, какой тип вибраций обладает разрушительной силой для данного патефона, и затем создать запись, в звуковых дорожках которой были бы закодированы именно такие звуки. Это довольно близкая аналогия с методом Гёделя, где собственные свойства системы отражаются в понятии пар доказательства и затем используются против нее самой. Любая система, как бы сложна она ни была, может быть подвергнута Гёделевой нумерации, после чего в ней может быть определено понятие пар доказательства — и это будет ружьем, которое выстрелит в самого охотника. Как только система определена, упакована в «коробку», она становится уязвимой.

Этот принцип прекрасно иллюстрирован в диагональном методе Кантора, который позволяет найти недостающее действительное число для каждого хорошо определенного списка действительных чисел между 0 и 1. Именно создание хорошо определенного списка действительных чисел является причиной неудачи. Давайте посмотрим, как Канторов метод может быть повторен снова и снова. Подумайте, что произойдет, если, начиная с некоего списка L, вы проделаете следующее:

(1а) Возьмете список L и построите его диагональное число d.

(1b) Добавите d к списку L, получая таким образом новый список L + d.

(2а) Возьмете список L + d и построите его диагональное число d'.

(2b) Добавите d' к списку L + d, получая таким образом новый список L + d'.

Этот процесс постепенного «залатывания дырок» в L кажется слишком медленным, поскольку, имея в распоряжении L, мы могли бы получить d, d', d'', d''' сразу. Но если вы думаете, что создавав такой список, получите полное описание всех действительных чисел, то вы ошибаетесь. Проблема возникает в тот момент, когда вы спрашиваете себя, в каком месте L нужно вставить список диагональных чисел. Какой бы хитроумной схемой вы при этом не пользовались, как только ваш новый список L будет закончен, он тут же окажется уязвимым. Как я уже сказал, именно создание хорошо определенного списка действительных чисел оказывается причиной неудачи.

В случае с формальными системами, неполнота возникает, когда мы определяем предполагаемый рецепт выражения теоретико-численной истины. Именно в этом заключалась проблема ТТЧ + G_ω. Как только вы вводите все хорошо определенные G в ТТЧ, там тут же появляется некое новое G, непредусмотренное вашей схемой аксиом. В случае сражения Черепахи с Крабом в «Акростиконтрапунктусе», как только «архитектура» патефона была определена, он становился уязвимым для разбивальной музыки.

Так что же делать? Конца этому не предвидится. Кажется, что ТТЧ, даже если расширять ее до бесконечности, всегда будет оставаться неполной. Поэтому говорят, что ТТЧ непополнима, поскольку неполнота является неотъемлемой характеристикой ТТЧ: это одно из ее основных свойств и избавиться от него невозможно. Более того, эта проблема будет преследовать любой вариант теории чисел, будь это расширенная версия ТТЧ, измененная версия ТТЧ, или альтернативная версия ТТЧ. Дело в том, что в любой данной системе возможность построить неразрешимую строчку путем Гёделева метода автореференции зависит от трех основных условий:

1) Чтобы система была достаточно мощной, так что все желаемые высказывания о числах, как истинные, так и ложные, могли бы быть в ней выражены. (Если это условие не выполняется, значит, система с самого начала слишком слаба, чтобы соперничать с ТТЧ, поскольку она даже не способна выразить теоретико-численные понятия, выразимые в ТТЧ. На метафорическом языке «Акростиконтрапунктуса» это было бы равносильно использованию вместо патефона, скажем, холодильника.

2) Чтобы все общерекурсивные отношения были выражены формулами системы. (Если это условие не выполняется, значит, система не выражает в своих теоремах некоторых общерекурсивных истин — жалкая неудача в попытке выразить все истины теории чисел! На метафорическом языке «Акростиконтрапунктуса» это было бы равносильно использованию патефона низкого качества.)

3) Чтобы аксиомы и типографские схемы, выводимые по правилам данной системы, можно было распознать при помощи конечной процедуры решения. (Если это условие не выполняется, значит, не существует метода, чтобы отличить правильные деривации от «незаконных» — таким образом выходит, что «формальная система» вовсе не формальна и даже не определена как следует. На метафорическом языке «Акростиконтрапунктуса» это было бы равносильно частично собранному патефону.

Если эти три условия удовлетворены, значит, любая непротиворечивая система будет неполной, поскольку в ней возможна Геделева конструкция.

Интересно то, что любая подобная система роет сама себе яму, мощность системы является причиной ее «падения» Падение происходит потому, что система достаточно мощна, чтобы выразить автореферентные суждения. В физике существует понятие «критической массы» радиоактивного вещества, такого, например, как уран. Если масса ниже критической, с ураном ничего не происходит. Если же критическая масса достигнута, то в уране начинается цепная реакция и он взрывается. Кажется, что у формальных систем есть аналогичный критический «порог». Ниже этого порога система «безвредна» и даже не пытается формально выразить арифметические истины, но, как только порог достигнут, система внезапно приобретает возможность выражать автореферентные суждения и, следовательно, обрекает себя на неполноту. Этот критический порог по-видимому достигается примерно тогда, когда в системе выполняются все три данных выше условия. Как только система становится способной к автореферентности, в ней появляется «дыра», словно вырезанная по заказу она учитывает особенности системы и использует их против самой этой системы.

Страсти по Лукасу

Удивительная повторяемость Геделева аргумента использовалась многими — в частности Дж. Р. Лукасом — как оружие для защиты идеи, что человеческий разум отличается неким специфическим качеством, которое невозможно имитировать при помощи «механических автоматов» — то бишь, компьютеров. Лукас начинает свою статью «Разум, машины и Гедель» (J. R. Lucas, «Minds, Machines, and Godel») следующими словами:

Мне кажется что теорема Геделя доказывает, что Механизм не может выражать истину, что означает что разум не может быть объяснен как механизм.

Затем он приступает к изложению своих аргументов, которые я здесь кратко перескажу. Он утверждает, что для того, чтобы мы могли считать интеллект компьютера равным интеллекту человека, компьютер должен быть способен проделать любое интеллектуальное задание, на которое способен человек. Однако, говорит Лукас, компьютер не способен проделать «Геделизацию» (один из его забавно фамильярных терминов) так, как на это способны люди. Почему? Подумайте о любой формальной системе, такой как ТТЧ, или ТТЧ + G, или даже ТТЧ + G_ω. Легко составить компьютерную программу, выводящую теоремы этой системы таким образом, что рано или поздно любая заранее выбранная теорема оказывалась бы выведенной. Это значит, что компьютер не пропускал бы не одной области в «пространстве» всех теорем Подобная программа состояла бы из двух основных частей (1) подпрограмма, «штампующая» аксиомы на основе «схемы аксиом», если таковая имеется и (2) подпрограмма, использующая правила вывода для получения новых теорем на основании имеющихся теорем (и, разумеется, аксиом). Эти две подпрограммы использовались бы по очереди.

По сравнению с человеком, мы можем сказать, что программа «знает» некоторые факты о теории чисел — а именно, те факты, которые она печатает. Если она пропускает некий истинный факт теории чисел, это значит, что она его не «знает». Следовательно, можно доказать, что компьютерная программа «глупее» человека, показав, что люди знают что-то, недоступное машине. Здесь Лукас начинает свое доказательство. Он утверждает, что люди всегда могут проделать Гёделев трюк в любой формальной системе, равномощной ТТЧ — и, таким образом, они всегда знают больше, чем данная система. Это рассуждение может показаться приложимым лишь к формальным системам, но оно может быть немного изменено и в таком виде стать, как кажется, непобедимым аргументом против Искуственного Интеллекта, равного человеческому. Это делается так:

Рациональность и численность естественно рождают компьютеры, автоматы, роботов, следовательно…

Компьютеры изоморфны формальным системам. Значит…

Любой компьютер, чтобы быть таким же умным, как человек, должен быть способен понимать теорию чисел так же хорошо, как люди, значит…

Среди прочего, он должен знать примитивно рекурсивную арифметику. Но именно поэтому…

Он ловится на Гёделев «крючок», из чего следует, что…

Мы, с нашим человеческим интеллектом, можем вывести некое истинное утверждение теории чисел, истинность которого компьютер не в состоянии заметить (то есть, компьютер никогда не выведет этого утверждения) именно из-за Гёделева аргумента, действующего как бумеранг.

Из этого следует, что существует нечто, что невозможно запрограммировать на компьютерах, но что люди способны сделать. Значит, люди умнее.

Насладимся же, вместе с Лукасом, преходящим моментом антропоцентрической славы:

Какую бы сложную машину мы не сконструировали, она, будучи машиной, будет соответствовать формальной системе, которая, в свою очередь, будет подвержена Гёделевой процедуре нахождения формулы, недоказуемой в данной-системе. Эту формулу машина не в состоянии будет вывести в качестве истинной, хотя разум может установить ее истинность. Таким образом, машина все еще не будет адекватной моделью разума. Мы пытаемся создать механическую модель мозга — «мертвую» модель — но разум, будучи «живым», может всегда пойти на шаг дальше любой формализованной, окостеневшей, мертвой системы. Благодаря теореме Гёделя, за разумом всегда остается последнее слово.

На первый взгляд (и, может быть, даже после детального анализа), доводы Лукаса кажутся убедительными. Обычно они вызывают противоположные реакции. Некоторые ухватываются за них, почти как за религиозное доказательство существования души, в то время как другие просто отмахиваются от них, как от недостойной внимания чепухи. Мне кажется, что, хотя эти доводы ошибочны, они настолько интересны, что стоит потратить некоторое время на их опровержение. На самом деле, это было одной из основных причин, по которой я стал думать над проблемами, затронутыми в этой книге. Я попытаюсь опровергнуть доводы Лукаса одним способом в этой главе и другими способами в главе XVII.

Мы должны попробовать глубже понять, почему Лукас говорит, что компьютер невозможно запрограммировать так, чтобы он «знал» столько же, сколько люди. Его идея заключается в том, что мы всегда находимся вне системы, и что извне мы можем проделать «Геделизирующую» операцию, в результате дающую нечто, что мы, глядя извне, можем идентифицировать как истинное, но что не может быть интерпретировано как таковое изнутри системы. Но почему нельзя запрограммировать в качестве третьего главного компонента программы «Геделизирующий оператор», как Лукас его называет? Лукас объясняет:

Гёделева формула строится при помощи стандартной процедуры — только так мы можем быть уверены, что ее можно будет построить в любой формальной системе. Не если это стандартная процедура, то почему ее нельзя добавить к программе? Это соответствовало бы системе с дополнительным правилом вывода, позволяющего добавить к ней в качестве теоремы Геделеву формулу остальной системы, затем — Геделеву формулу получившейся при этом новой, более мощной формальной системы, и так далее. Это было бы равносильно добавлению к первоначальной формальной системе бесконечной цепочки аксиом, каждая из которых являлась бы Гёделевой формулой системы, полученной таким образом… Можно ожидать, что человек, столкнувшийся с машиной, обладающий Гёделевым оператором, принял бы этот факт во внимание и смог бы пере-Гёделить этот новый аппарат вместе с его Гёделевым оператором. В действительности, так и получается. Даже если мы добавим к формальной системе бесконечный ряд аксиом, состоящих из последовательных Гёделевых формул, получающаяся система все еще остается неполной, так как в ней будет недоказуемая в данной системе формула. Однако разумное существо, стоящее вне системы, видит, что эта формула истинна. Этого мы и ожидали, поскольку, даже если мы добавим бесконечный ряд аксиом, они должны быть определены с помощью некоего конечного правила, которое затем может быть учтено разумом, анализирующим расширенную формальную систему. В некотором роде, поскольку за разумом остается последнее слово, он может всегда обнаружить дыру в любой формальной системе, выдаваемой за его модель. Механическая модель должна быть в каком-то смысле конечной и определенной, следовательно, разум всегда окажется более гибким.

Перепрыгивая измерением выше

Образ, который мы находим у Эшера, помогает нам лучше понять эту идею; речь идет о его «Драконе» (рис. 76). Основная тема в нем, разумеется, — это дракон, кусающий себя за хвост, со всеми Гёделианскими ассоциациями, которые это вызывает. Но в этой картине есть и более глубокий смысл. Сам Эшер написал по этому поводу очень интересные комментарии. Первый комментарий касается серии рисунков, в которых Эшер исследовал конфликт «между плоскостью и трехмерным пространством»; второй комментарий — собственно о «Драконе»:

I. Наше трехмерное пространство — это единственная известная нам реальность. Двумерность точно так же фантастична для нас, как и четырехмерность, поскольку в нашем мире ничто не плоско по-настоящему, даже поверхность тщательнейшим образом отполированного зеркала. И все же мы держимся за идею, что стена или лист бумаги на самом деле плоские, — и интересно то, что мы продолжаем, с незапамятных времен, производить иллюзии пространства на этих самых плоских поверхностях. Не абсурдно ли нарисовать несколько линий и назвать это «домом»? Эта странная ситуация — тема следующих пяти рисунков [включая «Дракона»].

II. Как бы этот дракон не пытался стать трехмерным, он остается совершенно плоским. На бумаге, на которой он нарисован, прорезаны два отверстия. Затем она сложена так, что получаются два квадратных «окошка». Но этот дракон упрям, и несмотря на свою плоскостность, он настаивает на том, что он трехмерен — поэтому он просовывает голову в одно из отверстий, и хвост — в другое.

Этот второй комментарий очень важен. Эшер имеет в виду то, что как бы мы не исхитрялись, пытаясь выразить три измерения в двух, при этом всегда теряется некая «основная сущность трехмерности». Дракон изо всей силы пытается побороть свою двумерность. Он пробует сделать это, высовывая голову из бумаги, на которой, как ему кажется, он нарисован — но мы, находящиеся вне рисунка, видим, насколько тщетны его усилия, поскольку и дракон, и дырки, и складки — всего лишь двумерные изображения соответствующих понятий, и не одно из них не является реальным. Но дракон не может выйти из своего двумерного пространства и не может, подобно нам, этого увидеть.

На самом деле, можно пойти еще дальше. Мы можем вырвать эту картинку из книги, сложить ее, прорезать в ней дырки, вывернуть ее наизнанку, и сфотографировать результат — и она снова станет двумерной. То же самое можно повторить и с фотографией. Каждый раз, когда изображение становится опять двумерным — как бы хитроумно мы не симулировали на нем трехмерность в двух измерениях — оно снова может быть разрезано и сложено.

Имея в виду эту замечательную Эшеровскую метафору, вернемся к программам и людям. Мы говорили о попытке ввести «Геделизирующий оператор» в саму программу. Но даже если бы мы написали программу, выполняющую эту операцию, она не уловила бы сути Гёделева метода. Мы снова можем, находясь вне системы, уничтожить ее методом, ей самой недоступным. Однако позвольте: являются ли наши доводы аргументами за или против идеи Лукаса?

Рис. 76. М. К. Эшер «Дракон» (гравюра на дереве, 1952)

Пределы разумных систем

Против Сам факт, что мы не можем написать программу, способную на «Гёделизирование», заставляет нас подозревать, что мы и сами не всегда на это способны. Одно дело — абстрактно аргументировать, что Гёделизирование возможно, и совсем другое дело — знать, как проделать эту операцию в каждом конкретном случае. На самом деле, по мере того, как сложность формальных систем (или программ) возрастает, наша способность «Геделизировать» начинает ослабевать. Это естественно, поскольку, как мы только что выяснили, у нас нет алгоритма, описывающего этот процесс. Если мы не можем объяснить, как применить метод Гёделя в каждом отдельном случае, то для каждого из нас рано или поздно наступит такой момент, когда, столкнувшись со слишком сложным случаем, мы не сможем сообразить, что делать.

Разумеется, этот предел способностей каждого из нас будет весьма приблизительным, так же, как предел веса, который мы способны оторвать от земли. Иногда мы не способны поднять 120 кг а на другой день это у нас получается. Но мы можем быть уверены что нам никогда не удастся поднять 120 тонн. В этом смысле хотя личный предел способностей каждого приблизителен существуют системы которые лежат далеко за пределами человеческой способности к Геделизированию.

Это понятие проиллюстрировано в Диалоге «Праздничная Кантататата». Сначала кажется что Черепахе удастся сколько угодно водить Ахилла за нос. Но затем Ахилл пытается обобщить все ответы в одной схеме. Этот новый трюк получает имя ω. Очень важно то что это имя — новое Это первый пример ситуации, в которой приходится расширить старую схему имен, включавшую имена только для натуральных чисел. Далее вводятся несколько новых расширенных вариантов, чьи имена иногда естественны, а иногда довольно сложны. Но рано или поздно запас имен у нас опять кончится; это произойдет в тот момент, когда схемы ответов

ω, ω ^ω,ω ^{ω ^ω}, …

объединятся в одну невероятно сложную схему ответов. Придется нам дать этой схеме совершенно новое имя — «ε₀». Новое имя вводится каждый раз, когда совершается принципиально новый шаг, связанный с тем, что мы находим некую нерегулярность в системе. Таким образом, новое имя должно быть придумано ad hoc.

Не существует рекурсивного правила для называния порядковых чисел

Вы можете подумать, что эти нерегулярности в переходе от одного порядкового числа (так называются эти имена, даваемые нами бесконечности) к другому могут быть разрешены с помощью компьютера; такая программа производила бы новые имена упорядоченно. Когда у нее «кончался бы бензин», она включала бы «центр нерегулярности», производящий новое имя и затем переключающий программу обратно на регулярный контроль. Но эта идея не работает. Дело в том, что сами нерегулярности возникают нерегулярно, и нам понадобилась бы программа высшего порядка — то есть программа, создающая новые программы, дающие новые имена. И даже этого оказывается недостаточно. В какой-то момент становится необходимой программа третьего порядка — и так далее, и тому подобное.

Вся это невероятная сложность берет начало в теореме, которой мы обязаны Алонзо Черчу и Стефену Клини. Эта теорема о структуре «бесконечных порядковых чисел» утверждает, что:

Не существует такой рекурсивно согласованной системы обозначений, которая давала бы имя каждому конструктивному порядковому числу.

Нам придется оставить обсуждение того, что такое «рекурсивно родственные системы нотации» и «конструктивные порядковые числа», более техническим трудам, таким, например, как книга Хартлея Роджерса (Hartley Rodgers, см. Библиографию). Здесь мы удовольствуемся интуитивной идеей. По мере того, как порядковые числа возрастают, в них появляются нерегулярности, и нерегулярности в этих нерегулярностях, и нерегулярности в нерегулярностях нерегулярностей и так далее. Не существует такой единой схемы, которая могла бы назвать все порядковые числа. Из этого следует, что не существует такого алгоритмического метода, который мог бы сказать нам, как приложить метод Гёделя к любой возможной формальной системе. Если не ударяться в мистику, то приходится согласиться с тем, что любое человеческое существо рано или поздно достигнет предела своей способности Геделизировать. С этого момента формальные системы такой сложности, хотя и неполные из-за возможности приложения к ним Гёделева метода, сравняются по мощи с человеческим разумом.

Другие возражения Лукасу

Это только один способ спорить с Лукасом. Существуют другие, возможно, более убедительные, аргументы против его идей, которые мы рассмотрим позже Но этот последний контраргумент очень важен поскольку он касается интереснейшей идеи создания компьютерной программы, способной выйти за пределы самой себя, увидеть себя полностью со стороны и применить трюк Геделя к самой себе. Разумеется, это так же невозможно, как невозможно для патефона воспроизвести собственную разбивальную мелодию. Однако мы не должны считать ТТЧ ущербной по этой причине Дефект, если он и есть, заключается не в самой системе, а в наших ожиданиях того, на что эта система окажется способна. Кроме того необходимо помнить, что и мы сами бессильны против словесного трюка который Гедель перевел в математическую форму—я имею в виду парадокс Эпименида. Это было весьма хитроумно подмечено Ч. Г. Уайтли, когда он предложил высказывание «Лукас не может непротиворечиво утверждать это высказывание» Подумав, вы поймете, что (1) это верно, и все же (2) Лукас не может этого утверждать непротиворечиво. Значит, Лукас также «неполон» по отношению к существующим в мире истинам. То, как мир отражен в его мозгу, не позволяет ему одновременно быть непротиворечивым и утверждать истинное высказывание. Но Лукас подвержен этому не более, чем любой из нас. Он, как и все мы, просто находится на уровне сложной формальной системы.

Забавный способ увидеть ошибку доводов Лукаса — это сравнить их со спором мужчин и женщин. В своих странствованиях Лукус Мыслитель однажды находит неизвестный предмет — женщину. Не будучи ранее знаком с подобным явлением, вначале он застывает в восхищении перед сходством объекта с ним самим, но затем, немного испуганный, он кричит всем мужчинам кругом: «Постойте! Я могу смотреть ей в лицо — а это нечто, на что она сама не способна. Значит, женщины никогда не могут быть подобны мне!» Так он доказывает превосходство мужчин над женщинами, к глубочайшему удовлетворению как собственной персоны, так и своих товарищей-мужчин. (Тот же довод доказывает и превосходство Лукуса над всеми остальными мужчинами — факт, о котором он тактично умалчивает) Женщина отвечает: «Да, вы можете смотреть мне в лицо, чего я сделать не могу — но я могу смотреть вам в лицо, на что вы не способны. Мы равны!» На что Лукус находит неожиданный ответ: «Мне очень жаль, но если вы считаете, что можете видеть мое лицо, вы ошибаетесь. То, что вы, женщины, делаете — совсем не то же самое, что делаем мы, мужчины. Как я уже сказал, это явление низшего разряда и не заслуживает называться тем же именем Это можно назвать „женовидением“. Тот факт что вы можете „женовидеть“ мое лицо совершенно не важен, поскольку ситуация несимметрична. Теперь вы видите разницу?» «Да, теперь я женовижу» — женоотвечает женщина и женоудаляется.

Этот аргумент напоминает страуса, засунувшего голову в песок — но он вам понадобится, если вы настаиваете на том, что мужчины и женщины будут всегда опережать компьютеры по части интеллекта.

Выход из себя самого — современный миф

Интересно поразмыслить над тем можем ли мы, люди, выйти за пределы самих себя — и могут ли это сделать компьютерные программы Разумеется, программа может модифицировать себя — но возможность всякой модификации должна быть заложена в программе с самого начала, так что это не может служить примером «выхода из системы». Как бы программа не вертелась и не извивалась, чтобы вырваться за свои пределы, она все же следует заложенным в ней правилам. Она так же не может выйти за пределы самой себя, как человек не может по желанию перестать следовать законам физики. Физика — это система, выхода из которой не существует. Однако возможно осуществить нечто подобное в меньшем масштабе — а именно, выйти из подсистемы собственного мозга в более широкую подсистему. Иногда удается сойти с наезженной колеи. Это все еще объясняется взаимодействием различных подсистем мозга, но на вид это весьма похоже на полный выход из себя. Подобно этому, можно представить, что нам удастся создать программу, умеющую частично «вылезать из своей шкуры».

Однако важно не упускать из вида разницы между восприятием самого себя и выходом из самого себя. Воспринимать себя вы можете различными способами: в зеркале, на фотографиях, в фильмах, на пленке, по описаниям других, по результатам психоанализа и так далее. Но вы не можете выйти из собственной кожи и встать снаружи себя самого (несмотря на утверждения современных оккультистов). ТТЧ может говорить о себе, но она не может выйти из себя. Компьютерная программа может модифицировать себя, но она не может нарушить своих собственных инструкций — большее, на что она способна, это изменить себя частично, следуя тем же инструкциям. Это напоминает юмористический парадоксальный вопрос: «Может ли Бог создать такой тяжелый камень, который он сам не способен будет поднять?»

Реклама и обрамляющие приспособления

Идея выйти за пределы системы очень заманчива и лежит в основе прогресса в искусстве, музыке и других областях человеческой деятельности. Она также лежит в основе таких тривиальных вещей, как создание радио- и телевизионных реклам. Эта тенденция была тонко подмечена и замечательно описана в книге Эрвинга Гоффмана (Erving Goffman, «Frame Analysis»):

Например, профессиональный актер заканчивает сниматься в рекламе, где он пил некий напиток, и, в то время как камера еще снимает его, с видимым облегчением поворачивается и берет стакан того же напитка, чтобы теперь по-настоящему им насладиться.

Разумеется, это всего лишь один из примеров того, как рекламные объявления, передающиеся по радио и телевидению, используют «обрамляющие» трюки, чтобы создать у слушателя и зрителя впечатление естественности, которое, как надеются рекламщики, пересилит то недоверие, которое люди обычно чувствуют к рекламе. Поэтому в рекламе часто используются детские голоса, предположительно естественные, уличный шум и другие эффекты, чтобы создать иллюзию интервью со случайными людьми; актеры специально говорят с паузами, перебивают друг друга, и всячески симулируют естественный разговор. Рекламное объявление фирмы прерывается сообщением о ее новом продукте или какой-либо новостью — таким образом авторы рекламы надеются убедить зрителя в том, что это вовсе не реклама.

Чем меньше зрители доверяют естественности подобных деталей, тем активнее налегают на них рекламщики. В результате реклама получается весьма беспорядочная, ту же тенденцию можно заметить и в работе консультантов политических лидеров и, в меньшем масштабе, в микро-социологии.

Здесь перед нами еще один пример сражения Черепахи с Крабом, на этот раз на новой высоте — здесь противниками являются Правда и Реклама.

Симплицио, Салвиати, Сагредо: почему трое?

Между проблемой выхода за пределы системы и поисками полной объективности существует интересная связь. Прочитав у Джоча в его «Are quanta real?» четыре диалога, основанные на четырех Галилеевских «Диалогах, касающихся двух новых наук», я спросил себя, почему в них три участника — Симплицио, Салвиати и Сагредо. Почему было недостаточно только двух: Симплицио, ученого простака, и Салвиати, мудрого мыслителя? Зачем понадобился Сагредо? Предполагается, что он — нейтральный слушатель, бесстрастно взвешивающий доводы обеих сторон и высказывающий «справедливое», «беспристрастное» решение. Это звучит разумно, но здесь есть одна проблема: почему-то Сагредо всегда соглашается с Салвиати. Почему же это Воплощение Справедливости завело себе любимчика? Возможным ответом является то, что Салвиати, действительно, всегда прав, так что у Сагредо нет выбора. Но где тогда справедливость и равенство?

Добавляя Сагредо, Галилей (и Джоч) скорее помешали, чем помогли Симплицио. Может быть, следовало бы добавить еще одного Сагредо высшего уровня — кого-нибудь, кто мог бы оценить всю ситуацию объективно… Вы, наверное, уже заметили, куда это ведет. Мы получим таким образом бесконечную серию «возрастающих объективностей», которая обладает интересным свойством никогда не становиться объективнее, чем она была вначале, когда Салвиати был просто прав, а Симплицио — просто ошибался. Так что присутствие Сагредо остается загадкой, ответ на которую, возможно, заключается в том, что его присутствие дает некую привлекательную иллюзию выхода из системы.

Дзен и выход из системы

Дзен-буддизм также размышляет о возможности выхода из системы. Возьмем, например, тот коан, в котором Тозан говорит своим монахам, что «высший Буддизм — не Будда». Может быть, выход из себя является центральной темой дзена. Дзен-буддист старается глубже понять, кем он является на самом деле, все более и более освобождаясь от его собственных идей о нем самом, нарушая все правила и соглашения, которые, по его мнению, держат его связанным, — включая правила самого дзена. Где-то на этой нелегкой тропе он может встретить Просветление. Во всяком случае (как мне кажется), надежда заключается в том, что постепенно углубляя самосознание, постепенно расширяя пределы «системы», можно прийти к ощущению слияния со вселенной.

Назад: Праздничная Кантататата…

Дальше: Благочестивые размышления курильщика табака