Прелюдия и…
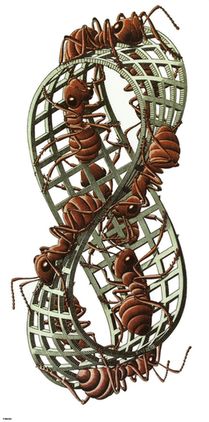
Рис. 54. М. К. Эшер. «Лист Мёбиуса II» (гравюра на дереве, 1963).
Ахилл и Черепаха пришли в гости к Крабу, чтобы познакомиться с его другом Муравьедом. После того, как новые знакомые представлены друг другу, вся четверка садится за чай.
Черепаха: Мы вам кое-что принесли, мистер Краб.
Краб: Очень любезно с вашей стороны, но зачем же было утруждаться?
Черепаха: О это так, мелочь — в знак нашего уважения. Ахилл, отдайте, пожалуйста, подарок м-ру К.
Ахилл: С удовольствием. С наилучшими пожеланиями, м-р К. Надеюсь, что вам понравится.
(Ахилл протягивает Крабу элегантно завернутый пакет, квадратный и плоский Краб начинает его разворачивать).
Муравьед: Интересно, что это такое?
Краб: Сейчас узнаем (Кончает разворачивать и вытаскивает подарок). Две пластинки! Прекрасно! Но погодите-ка здесь нет этикетки. Неужели это снова ваши «особые» записи, г-жа Ч?
Черепаха: Если вы имеете в виду разбивальную музыку, на этот раз нет. Но эти записи действительно уникальны, так как они сделаны по персональному заказу. На самом деле, их еще никто никогда не слышал — кроме, конечно Баха, когда тот их играл.
Краб: Когда Бах их играл? Что вы имеете в виду?
Ахилл: Вы будете вне себя от счастья, м-р Краб, когда г-жа Ч объяснит вам, что это за пластинки.
Черепаха: Почему бы вам самому этого не рассказать, Ахилл? Не стеснятесь, говорите!
Ахилл: Можно? Вот здорово! Но я лучше загляну сначала в свои записи (Вытаскивает бумажку и откашливается ) Кхе-кхе. Желаете послушать рассказ о замечательных новых результатах в математике — результатах, которым ваши пластинки обязаны своим существованием?
Краб: Мои пластинки восходят к каким-то математическим выкладкам? Как интересно! Что ж, теперь, когда вы задели мое любопытство, я просто обязан об этом узнать.
Ахилл: Отлично! (Делает паузу, чтобы отхлебнуть чай, затем продолжает) Кто-нибудь из вас слышал о печально известной «Последней Теореме» Ферма?
Муравьед: Не уверен. Звучит знакомо, но не могу припомнить.

Рис. 55. Пьер Де Ферма
Ахилл: Идея очень проста. Пьер де Ферма, адвокат по профессии и математик по призванию, однажды, читая классический текст Диофанта «Арифметика», наткнулся на следующее уравнение:
a² + b² = c²
Он тут же понял, что это уравнение имеет бесконечно много решений для а, b, и с, и написал на полях свою знаменитую поправку:
Уравнение:
а n+ b n = с n
имеет решение в положительных целых числах а, b, с, и n только при n = 2 (и в таком случае имеется бесконечное множество a, b, и c, удовлетворяющих этому уравнению), но для n>2 решений не существует. Я нашел замечательное доказательство этого, которое, к несчастью, не помещается на полях.
С того дня и в течение почти трехсот лет математики безуспешно пытаются сделать одно из двух: либо доказать утверждение Ферма и таким образом очистить его репутацию, в последнее время слегка подпорченную скептиками, не верящими, что он действительно нашел доказательство — либо опровергнуть его утверждение, найдя контрпример: множество четырех целых чисел а, b, с, и n, где n > 2, которое удовлетворяло бы этому уравнению. До недавнего времени все попытки в любом из этих двух направлений проваливались. Точнее, теорема доказана лишь для определенных значений n — в частности, для всех n до 125 000.
Ахилл: Не лучше ли тогда называть это Гипотезой вместо Теоремы, поскольку настоящее доказательство еще не найдено?
Ахилл: Строго говоря, вы правы, но по традиции это зовется именно так.
Краб: Удалось ли кому-нибудь в конце концов разрешить этот знаменитый вопрос?
Ахилл: Представьте себе, да: это сделала г-жа Черепаха, как всегда, в момент гениального озарения. Она не только нашла ДОКАЗАТЕЛЬСТВО Последней Теоремы Ферма (оправдав, таким образом, ее название и очистив репутацию Ферма), но и КОНТРПРИМЕР, показав, что интуиция скептиков их не подвела!
Краб: Вот это да! Поистине революционное открытие.
Муравьед: Прошу вас, не тяните: что это за магические числа, удовлетворяющие уравнению Ферма? Мне особенно любопытно узнать значение n.
Ахилл: Ах, какой ужас! Какой стыд! Верите ли, я оставил все выкладки дома на громаднейшем листе бумаги. К несчастью, он был слишком велик, чтобы принести его с собой. Хотел бы я, чтобы он был сейчас здесь и чтобы можно было вам все показать. Но кое-что я все же помню: величина n — единственное положительное число, которое нигде не встречается в непрерывной дроби числа π.
Краб: Какая жалость, что у вас нет с собой ваших записей. Так или иначе, у нас нет оснований сомневаться, что все, что вы нам сказали — чистая правда.
Муравьед: Да и кому, в конце концов, нужно видеть n в десятичной записи? Ахилл же объяснил нам, как найти это число. Что ж, г-жа Черепаха, примите мои сердечные поздравления по поводу вашего эпохального открытия!
Черепаха: Благодарю вас. Однако практическая польза, которую немедленно принес мой результат, кажется мне еще важнее теоретического открытия.
Краб: Смерть как хочется услышать об этом — ведь я всегда считал, что теория чисел — Царица Чистой Математики, единственная ветвь математики, не имеющая НИКАКОГО практического приложения.
Черепаха: Вы не единственный, кто так думает; однако на деле почти невозможно предсказать, когда и каким образом какая-либо ветвь чистой математики — или даже какая-либо индивидуальная Теорема — повлияет на другие науки. Это происходит совершенно неожиданно, и данный случай — хороший тому пример.
Ахилл: Обоюдоострый результат г-жи Черепахи прорубил дверь в область акусто-поиска.
Муравьед: Что такое акусто-поиск?
Ахилл: Название говорит само за себя: это поиск и извлечение акустической информации из сложных источников. Например, типичная задача акусто-поиска — восстановить звук, произведенный упавшим в воду камнем, по форме расходящихся по воде кругов.
Краб: Но это невозможно!
Ахилл: Почему же? Это весьма похоже на то, что делает наш мозг, когда он восстанавливает звук, произведенный голосовыми связками другого человека, по колебаниям, переданным барабанной перепонкой далее по лабиринту ушной раковины.
Краб: Ясно. Но я все еще не вижу связи этого ни с теорией чисел, ни с моими новыми пластинками.
Ахилл: Видите ли, в математике акусто-поиска часто возникают вопросы, связанные с числом решений неких Диофантовых уравнений. А г-жа Ч годами занималась тем, что пыталась восстановить звуки игры Баха на клавесине (что происходило более двухсот лет тому назад), основываясь на расчетах движения всех молекул в атмосфере в настоящее время.
Муравьед: Но это же совершенно невозможно! Эти звуки утрачены навсегда, утеряны невозратимо!
Ахилл: Так думают непосвященные — но г-жа Ч посвятила много лет этой проблеме и пришла к выводу, что все зависит от количества решений уравнения:
а n+ b n = с n
в положительных числах, при n > 2.
Черепаха: Я могла бы объяснить, при чем здесь это уравнение, но не хочу наскучить присутствующим.
Ахилл: Оказалось, что теория акусто-поиска предсказывает, что звуки Баховского клавесина могут быть восстановлены по движению всех молекул атмосферы при одном из двух условий ЛИБО у этого уравнения есть хотя бы одно решение.
Краб: Удивительно!
Муравьед: Фантастика да и только!
Черепаха: Кто бы мог подумать!
Ахилл: Я хотел сказать, «ЛИБО такое решение существует, ЛИБО существует доказательство, что уравнение НЕ имеет решений!» Итак, г-жа Ч начала кропотливую работу с обоих концов проблемы одновременно Оказалось, что нахождение контрпримера было ключом к нахождению доказательства, так что одно прямо вело к другому.
Краб: Как же это возможно?
Черепаха: Видите ли, мне удалось показать, что структуру любого доказательства Последней Теоремы Ферма — если таковое существует — возможно описать с помощью элегантной формулы, которая зависела бы от величин решения некоего уравнения. Когда я нашла это второе уравнение, к моему удивлению оно оказалось не чем иным как уравнением Ферма. Забавное случайное соотношение между формой и содержанием. Так что, когда я нашла контрпример, мне осталось только использовать эти числа как план для построения доказательства того, что это уравнение не имеет решения. Замечательно просто, если подумать. Не знаю, почему никто не нашел этого результата раньше.
Ахилл: В результате этого неожиданного блестящего математического успеха, г-же Ч удалось провести акусто-поиск о котором она столько лет мечтала. Подарок полученный м-ром Крабом представляет собой осязаемую реализацию этой абстрактной работы.
Краб: Не говорите мне пожалуйста что это запись Баха, играющего на клавесине собственные сочинения!
Ахилл: Сожалею, но приходится поскольку это именно она и есть! Это набор из двух записей Себастиана Баха исполняющего весь Хорошо Темперированный Клавир. На каждой пластинке записана одна из двух его частей, это значит что каждая запись состоит из 24 прелюдий и фуг по одной в каждом мажорном и минорном ключе.
Краб: В таком случае мы должны немедленно прослушать эти бесценные пластинки! Как я смогу вас отблагодарить?
Черепаха: Вы уже нас отблагодарили сполна этим превосходным чаем, который вы для нас приготовили.
(Краб вынимает одну из пластинок из конверта и ставит ее на свой патефон. Комната наполняется звуками потрясающей, мастерской игры на клавесине, при этом качество записи самое высокое, какое можно вообразить. Можно даже разобрать — или это только воображение слушателя? — тихий голос Баха, подпевающего собственной игре)
Краб: Хотите следить по нотам? У меня есть уникальное издание Хорошо Темперированною Клавира, проиллюстрированное одним из моим учителей, который также был необыкновенным каллиграфом.
Черепаха: Это было бы чудесно.
(Краб подходит к элегантному книжному шкафу с застекленными дверцами, открывает его и достает два больших тома.)
Краб: Вот, пожалуйста, г-жа Черепаха. Я сам еще не видел всех прекрасных иллюстраций в этом издании, все никак клешни не доходят. Может быть, ваш подарок меня наконец на это подвигнет.
Черепаха: Надеюсь.
Муравьед: Вы заметили, что во всех этих произведениях прелюдия точно определяет настроение следующей фуги?
Краб: О, да. Хотя это трудно объяснить, но между ними всегда есть некая таинственная связь. Даже если у прелюдии и фуги нет общей музыкальной темы, в них всегда присутствует неуловимое абстрактное нечто, которое их прочно связывает.
Черепаха: И в кратких моментах тишины, которые отделяют прелюдию от фуги, есть что-то необыкновенно драматическое. Это тот момент, когда тема фуги готова вступить в свои права, сначала в отдельных голосах, которые потом сплетаются, создавая все более сложные уровни странной, изысканной гармонии.
Ахилл: Я знаю, что вы имеете в виду. Я слышал еще далеко не все прелюдии и фуги, но меня очень волнует этот момент тишины; в это время я всегда пытаюсь угадать, что старик Бах задумал на этот раз. Например, я всегда спрашиваю себя, в каком темпе будет следующая фуга? Будет ли это аллегро или адажио? Будет ли она на 6/8 или на 4/4? Будет ли в ней три голоса, или пять — или четыре? И вот звучит первый голос… Потрясающий момент!
Краб: Да, я помню давно ушедшие дни моей юности, дни, когда я трепетал от счастья, слушая эти прелюдии и фуги, возбужденный их новизной и красотой, и теми сюрпризами, которые они скрывают.
Ахилл: А теперь? Неужели это счастливый трепет прошел?
Краб: Он перешел в привычку, как всегда и бывает с подобными чувствами. Но в привычке также есть своя глубина, и это приносит определенное удовлетворение. Кроме того, я всегда обнаруживаю какие-нибудь новые сюрпризы, которых раньше не замечал.
Ахилл: Повторения темы, которых вы раньше не слышали?
Краб: Может быть; в особенности, когда эта тема проходит в обращении, спрятанная среди нескольких других голосов, или когда она поднимается на поверхность, словно возникая из ничего. Есть там также и удивительные модуляции, которые приятно слушать снова и снова, спрашивая себя, как это старик Бах смог создать подобное.
Ахилл: Приятно слышать, что все эти радости останутся у меня после того, как пройдет моя первая влюбленность в Хорошо Темперированный Клавир, жаль, однако, что это блаженное состояние не может длиться вечно.
Краб: Не бойтесь, влюбленность не пройдет бесследно. Эта юношеская влюбленность хороша тем, что ее всегда можно оживить именно тогда, когда вы считаете, что она уже умерла. Для этого необходим лишь толчок извне в нужном направлении.
Ахилл: Правда? Что же это за толчок?
Краб: Например, прослушивание этой музыки ушами того, кто слушает ее в первый раз; такой человек здесь вы, Ахилл. Каким-то образом, ваш трепет передается мне, и я снова полон блаженного восторга!
Ахилл: Звучит интригующе. Восторг спит где-то внутри вас, но сами вы не в состоянии вытащить его из глубин подсознания.
Краб: Именно так. Возможность оживить это чувство «закодирована» каким-то образом в структуре моего мозга, но я не могу осуществить это по желанию; я должен ждать счастливого случая, который запустит этот механизм.
Ахилл: У меня вопрос насчет фуг; мне стыдно об этом спрашивать, но, поскольку я новичок в искусстве слушания фуг, не может ли кто-нибудь из вас, матерых слушателей, научить меня кое-чему?
Черепаха: Я с удовольствием поделюсь с вами своими скудными познаниями, если это может вам чем-то помочь.
Ахилл: О, благодарю вас. Позвольте мне начать издалека. Знакомы ли вы с гравюрой М. К. Эшера под названием «Куб с магическими лентами»?
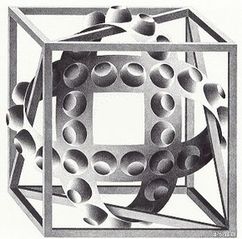
Рис. 56. М. К. Эшер «Куб с магическим лентами» (литография, 1957)
Черепаха: На которой изображены изогнутые ленты с искривлениями в виде пузырей, которые кажутся попеременно то выпуклыми, то вогнутыми?
Ахилл: Она самая.
Краб: Я помню эту картину. Кажется, что пузыри на ней все время перескакивают из одного состояния в другое: они то выпуклые, то вогнутые, в зависимости от того, с какого угла на них посмотреть. Невозможно одновременно увидеть их и выпуклыми, и вогнутыми — почему-то мозг этого просто не позволяет. У нас просто есть два разных способа воспринять эти пузыри.
Ахилл: Вы совершенно правы Знаете, мне кажется, что я открыл два способа слушать фугу, в чем-то аналогичных этому Вот они: либо следить лишь за одним отдельным голосом в каждый момент, либо слушать общее звучание, не пытаясь распутать голоса. Я пробовал оба эти способа и, к моему разочарованию, оказалось, что каждый из них исключает другой. Это просто не в моей власти слушать каждый индивидуальный голос и в то же время слышать общий эффект. Я все время перескакиваю с одного способа на другой, более или менее спонтанно и непроизвольно.
Муравьед: Так же, как когда вы смотрите на магические ленты?
Ахилл: Да. Но скажите… мое описание двух способов слушания фуги безошибочно указывает на меня, как на наивного, неопытного слушателя, не способного уловить более глубокие уровни восприятия?
Черепаха: Вовсе нет, Ахилл Я могу говорить только за себя, но я тоже постоянно перепрыгиваю с одного способа на другой, не контролируя этот процесс и не пытаясь сознательно решить, какой из двух способов должен господствовать. Не знаю, испытывали ли остальные наши друзья что-нибудь подобное.
Краб: Безусловно. Это весьма мучительное состояние, поскольку вы чувствуете, что дух фуги витает где-то близко — но вы не можете охватить его полностью, так как не в состоянии слушать сразу двумя способами.
Муравьед: У фуг есть интересная особенность: каждый из голосов является музыкальной пьесой сам по себе, так что фугу можно рассматривать как набор нескольких различных музыкальных произведений, основанных на одной и той же теме и исполняемых одновременно. И слушатель (или его подсознание) должен сам решать, воспринимать ли фугу как целое или как набор отдельных частей, гармонирующих друг с другом.
Ахилл: Вы говорите, что эти части «независимы», однако это не может быть совершенно верным. Между ними должна существовать какая-то координация, иначе, когда они исполняются вместе, мы слышали бы беспорядочное столкновение звуков — а это далеко не так!
Муравьед: Наверное, лучше сказать так: если бы вы слушали каждый голос в отдельности, вы обнаружили бы, что он имеет смысл сам по себе. Он может быть исполнен в одиночку, и именно это я имел в виду, говоря, что голоса независимы. Но вы совершенно правы, указывая, что каждая из этих индивидуальных мелодий соединяется с остальными совсем не случайным образом, сливаясь в изящное целое. Искусство создания прекрасных фуг заключается именно в умении соединять несколько линий, каждая из которых кажется написанной ради своей собственной красоты — но когда они взяты все вместе, целое звучит вполне естественно. Между прочим, двойственность между слушанием фуги как целого и слушанием составляющих её голосов — это частный пример более общей двойственности, приложимой к разным структурам, построенным, начиная с нижних уровней.
Ахилл: Правда? Вы хотите сказать, что мои два «способа» приложимы не только к ситуации со слушанием фуг?
Муравьед: Совершенно верно.
Ахилл: Интересно, как это может быть? Наверное, это связано с попеременным восприятием чего-либо как целого, или как собрания его частей. Но я сталкивался с этой дихотомией только слушая фуги
Черепаха: Вот это да! Посмотрите-ка! Я только что перевернула страницу следя за музыкой, и нашла великолепную иллюстрацию на странице перед титульным листом.
Краб: Я раньше никогда не видел этой иллюстрации. Будьте добры, передайте книгу по кругу.
(Черепаха передает книгу. Каждый из четырех приятелей рассматривает книгу по-своему — кто издалека, кто поднося прямо к глазам, при этом каждый из них качает головой в удивлении. Наконец, книга обходит всех и возвращается к Черепахе, которая смотрит в нее очень внимательно)
Ахилл: Мне кажется, прелюдия почти кончилась. Хотелось бы знать, удастся ли мне, слушая фугу, найти ответ на этот опрос «как нужно слушать фугу — как целое или как сумму частей?»
Черепаха: Слушайте внимательно и вы поймете!
(Прелюдия заканчивается. Следует пауза, и затем… )
Назад: Часть II
Дальше: ГЛАВА X: Уровни описания и компьютерные системы

