Начиная с 1985 года теория струн, называемая теперь теорией суперструн, существует в пяти версиях. Две из них наряду с закрытыми (замкнутыми) струнами содержат ещё и открытые (струны с двумя свободными концами), а три другие – только замкнутые. Названия этих пяти теорий не являются особо содержательными, но я их перечислю. Две теории с открытыми струнами называются теориями типа I. Три оставшиеся, содержащие только закрытые струны, известны как теория типа IIa, теория типа IIb и гетеротическая теория струн. Различия между ними носят слишком технический характер, и я боюсь, что их описание будет скучным для читателя. Но одна общая для всех этих теорий вещь гораздо интереснее, чем каждое из различий. Хотя некоторые теории содержат открытые струны, а некоторые – нет, все пять версий содержат закрытые струны.

Чтобы вы в полной мере смогли оценить, почему это так интересно, я должен пояснить, что именно разочаровывало исследователей во всех предыдущих теориях. В обычные теории – например, в квантовую электродинамику или в Стандартную модель, – гравитация добавлялась как «опция», как «плагин». Можно было либо игнорировать гравитацию, либо добавить её в готовое блюдо как специю. Рецепт прост: возьмите Стандартную модель и добавьте в неё ещё одну частицу – гравитон. Пусть гравитон будет безмассовым. Добавьте также несколько новых вершин в фейнмановскую диаграмму, чтобы любая частица могла испускать гравитоны. Блюдо готово. Но получившаяся теория работает не очень хорошо. Математика оказывается сложной и слишком чувствительной к малым возмущениям, и в конце концов фейнмановские диаграммы, содержащие гравитоны, превращаются в фарш из расчётов: все результаты оказываются бесконечными, и нет никакого способа придать этой теории хоть какой-нибудь смысл.

Мне кажется, что в каком-то смысле это хорошо, что простой путь завёл в тупик. В нём нет и намёка на объяснение свойств элементарных частиц. Он не даёт никакого объяснения, почему Стандартная модель именно такая, и он ничего не проясняет в вопросе тонкой настройки космологической постоянной или массы Хиггса. Откровенно говоря, если бы это работало, было бы очень обидно.

Но пять теорий струн вносят в этот вопрос полную ясность: они просто не могут быть сформулированы без гравитации. Гравитация в них – это не произвольная надстройка, а неизбежный результат. Теория струн, чтобы быть последовательной, обязана содержать гравитоны и силы, переносчиками которых они являются. Причина проста: гравитон – это закрытая струна, легчайшая из всех возможных. Открытые струны не являются обязательными для теории, но закрытые присутствуют всегда. Предположим, что мы пытаемся создать теорию, содержащую только открытые струны. Если бы мы добились успеха, то получили бы теорию струн без гравитации. Но мы успеха не добьёмся никогда, потому что два конца открытой струны всегда могут найти друг друга и замкнуться. Обычные теории оказываются самосогласованными только при отсутствии гравитации, в то время как теории струн согласуются, только если они включают гравитацию. Этот факт больше, чем любой другой, придаёт струнным теоретикам уверенность, что они находятся на верном пути.

Четыре теории, обозначаемые как тип I и тип II, были разработаны в 1970-х годах. И каждая из них имела фатальный дефект, относящийся не к внутренней математической согласованности, а к согласию теорий с экспериментальными данными. Каждая из теорий описывала возможный мир. Но ни один из этих миров не соответствовал нашему реальному миру. Поэтому пятая версия, разработанная в Принстоне в 1985 году, вызвала большое брожение умов. Эта версия получила название гетеротической теории струн, и её появление было воплощением всех мечтаний теоретиков. Она выглядела как реальная теория реального мира. Её успех был провозглашён неминуемым.

Но даже тогда были причины выдвинуть к этой теории ряд претензий. Во-первых, по-прежнему оставалась проблема слишком большого количества измерений: девяти пространственных и одного временно́го. Но теоретики уже знали, что делать с лишними шестью измерениями. Они приказали им: «Свернись!» Однако оставались ещё миллионы возможных вариантов многообразий Калаби – Яу, каждый из которых приводит к согласованной теории. А ещё хуже то, что даже после того, как вы выбрали один конкретный вариант многообразия Калаби – Яу, в качестве свободных параметров остаются сотни модулей, определяющих его форму и размер. И эти модули тоже приходится выбирать самому теоретику. Кроме того, все известные теории были суперсимметричными: в каждой из них присутствовали частицы-близнецы, которые, как мы знаем, отсутствуют в реальном мире.

Тем не менее струнные теоретики были настолько ослеплены мифом об однозначности, что на протяжении 1980-х и в начале 1990-х годов продолжали утверждать, что существуют только пять вариантов теории струн. В их воображении ландшафт был очень разрежен – содержал только пять точек! Конечно же, это был полный нонсенс, поскольку каждая компактификация характеризуется огромным количеством переменных модулей, но тем не менее физики с редким упорством держались за идею-фикс, что существуют только пять различных теорий. Даже если бы и в самом деле существовали только пять возможных теорий, по какому принципу следует выбирать ту единственную, которая описывает реальный мир? Идей не было. Но в 1995 году состоялся прорыв – не в поиске правильной версии теории для описания реального мира, но в понимании связи между различными версиями.

Каждый год в конце весны – начале лета мировые струнные теоретики собираются на ежегодный джамбори. Американцы, европейцы, японцы, корейцы, индийцы, пакистанцы, израильтяне, латиноамериканцы, китайцы, мусульмане, ортодоксальные иудеи, индуисты, верующие и атеисты, – мы все съезжаемся на неделю, чтобы послушать друг друга и поделиться свежими идеями. И почти все четыре или пять сотен участников знакомы друг с другом.

Учёные старшего поколения – все, как правило, старые друзья. Встречаясь, они делают то, что всегда делают физики: читают и слушают лекции по самым животрепещущим проблемам. А потом устраивают банкет.

1995 год стал незабываемым, по крайней мере для меня, по двум причинам. Первая причина состояла в том, что я был спикером на банкете. Второй причиной стало событие исторического значения для собравшихся там людей: Эд Виттен прочёл лекцию о впечатляющем прогрессе в наших исследованиях, очертив огромное поле совершенно новых направлений. К сожалению, лекция Виттена прошла мимо меня, но не потому, что я не смог на ней присутствовать, а потому, что я был занят мыслями о своей предстоящей банкетной речи.

То, о чём я собирался говорить, должно было взорвать вечер возмутительной гипотезой о том, что сегодняшние физики, возможно, были бы в состоянии выдвинуть революционные теории, даже если бы после окончания XIX века не было поставлено ни одного нового эксперимента. Моей целью было отчасти развлечь аудиторию, а отчасти обрисовать ожидающие нас, струнных теоретиков, перспективы. Я вернусь к этому в главе 9.

Тем, что я пропустил мимо ушей из-за мыслей о своей речи, была новая идея, которая могла бы стать центральным элементом моей концепции Ландшафта. Эд Виттен – не только великий матфизик, но и одна из главных фигур среди чистых математиков, которые уже давно стали движущей силой развития теории струн. Он – профессор (я бы даже сказал Профессор) и ведущий учёный перезаряженного интеллектом Принстонского института перспективных исследований, служившего домом Альберту Эйнштейну и Джону Роберту Оппенгеймеру. Виттен более чем кто-либо целеустремлённо гнал клячу науки вперёд.

К 1995 году стало ясно, что вакуум, описываемый теорией струн, отнюдь не единственный. Существовало несколько версий теории, каждая из которых приводила к различным Законам Физики. Это рассматривалось не как достоинство, а скорее как недостаток теории. В конце концов, десять лет назад принстонские струнные теоретики выдвинули теорию, которая не просто обещала стать единственной, но и претендовала на роль окончательной, истинной теории, описывающей природу. Основной задачей Виттена было доказать, что все, кроме быть может, одной, версии теории струн математически несогласованны. Но вместо этого он обнаружил Ландшафт, или, точнее, регион Ландшафта, лежащий на нулевой высоте, то есть суперсимметричную часть Ландшафта.

Это произошло следующим образом. Представьте себе, что некие воображаемые физики обнаружили бы две теории, описывающие электроны и фотоны: обычную квантовую электродинамику и ещё одну теорию. Во второй теории электроны и позитроны, вместо того чтобы свободно перемещаться в трёхмерном пространстве, могли бы двигаться только в одном направлении, скажем, вдоль оси x. Они просто не в состоянии были бы двигаться в любом другом направлении. В то же время фотоны сохраняли бы способность двигаться обычным образом. Вторая теория могла бы привести теоретиков в замешательство. Насколько они могли бы судить, эта теория была математически полностью самосогласованной, как и квантовая электродинамика, которая описывает реальный мир атомов и фотонов, но ей не нашлось бы места в их представлениях о реальном мире. Никто из них долго не мог бы объяснить феномен существования двух одинаково хорошо самосогласованных теорий, одна из которых описывает реальный мир, а второй – место на помойке. Они бы надеялись и молились, что кто-то обнаружит ошибку, математическое противоречие, которое позволило бы отбросить нежелательную теорию и дать им основание полагать, что мир устроен именно так, а не иначе, потому что никакой другой мир невозможен.

Пытаясь обнаружить внутреннюю несогласованность второй теории, исследователи могли бы натолкнуться на некоторые интересные факты. Они не только не нашли бы никаких противоречий, но и начали бы понимать, что две означенные теории являются частями одной и той же теории. Они поняли бы, что вторая теория представляет собой просто частный случай обычной теории в области пространства с чрезвычайно сильным магнитным полем – как бы внутри некоего магниторезонансного супертомографа. Любой физик скажет вам, что очень сильное магнитное поле будет заставлять заряженные частицы двигаться только в одном направлении: вдоль магнитных силовых линий. Но движение незаряженных частиц, таких как и фотон, не зависит от магнитного поля. Другими словами, они бы поняли, что существует только одна теория, только один набор уравнений, но два решения. Более того, непрерывно изменяя величину магнитного поля, можно получить весь набор решений между двумя предельными случаями. Эти вымышленные физики обнаружили бы непрерывный ландшафт и приступили бы к его изучению. Конечно же, они бы и понятия не имели о механизме, который позволил бы выбрать из всего спектра решений правильное, о механизме, который объяснял бы, почему в реальном мире отсутствует сильное фоновое магнитное поле. Но они бы надеялись объяснить это позже.

Это в точности то самое положение, в котором оставил нас Виттен в 1995 году в Лос-Анджелесе по завершении своей лекции. Он обнаружил, что все пять версий теории струн оказались решениями одной-единственной теории: мы имели не множество теорий, а множество решений. Все они принадлежали к семейству, которое включает в себя ещё одного члена – Виттен назвал его М-теорией. Кроме того, некоторые крайние значения модулей соответствуют шести теориям, описывающим наиболее удалённые уголки Ландшафта. Как в примере с магнитным полем, модули можно непрерывно изменять, превращая каждую из теорий в любую другую! «Одна теория – множество решений» – это стало нашим руководящим девизом.

Существует масса домыслов о том, что означает буква «М». Вот некоторые из них: Мать, чудо (Miracle), Мембраны, Магия, мистика и Мастер. Позднее этот список пополнили ещё и Матрицы. Никто, судя по всему, точно не знает, что имел в виду Виттен, когда придумывал термин «М-теория». В отличие от ранее известных пяти теорий, их новоявленная кузина не является теорией с девятью пространственными и одним временным измерением. Вместо этого М-теория оперирует уже десятью пространственными и одним временным измерением. Ещё более тревожным обстоятельством является то, что М-теория – это не теория струн: вместо одномерных «резинок» основными объектами М-теории являются мембраны – двумерные листы энергии, чем-то напоминающие упругие резиновые поверхности. Хорошей новостью является то, что М-теория, по-видимому, способна обеспечить объединяющий базис, в котором различные варианты теории струн появляются, когда одно или более из десяти пространственных измерений компактифицируются. Это был реальный прогресс, который обещал привести к построению общего для всех струнных теорий фундамента. Но была и тёмная сторона. Почти ничего не было известно о том, как соединить одиннадцатимерную общую теорию относительности с квантовой механикой. Математика мембран ужасно сложна, она выходит далеко за пределы математики струн. М-теория была так же таинственна и непостижима, как любая теория квантовой гравитации дострунной эпохи. Создавалось впечатление, что мы сделали шаг вперёд и два шага назад.

Но замешательство длилось недолго. Уже на следующей встрече струнных теоретиков летом 1996 года я имел удовольствие сообщить, что мы с тремя моими друзьями раскрыли секрет М-теории. Мы обнаружили основополагающие объекты теории, и уравнения, управляющие ими, оказались невероятно простыми. Томас Бэнкс, Вилли Фишер, Стивен Шенкер и я обнаружили, что основными сущностями М-теории были не мембраны, а более простые объекты, своего рода «партоны» нового вида. В каком-то смысле они похожи на старые партоны Фейнмана – эти новые компоненты обладали удивительной способностью соединяться вместе, образуя все возможные виды объектов. Гравитон, считавшийся наиболее фундаментальной элементарной частицей, оказался собранным из многих партонов. Если же собрать партоны другим способом, получались мембраны. Собранные ещё одним способом, партоны образовывали чёрные дыры. Уравнения новой теории оказались намного проще, чем уравнения теории струн, даже проще уравнений общей теории относительности. Новая теория получила название матричной теории. Иногда её название пишут как M(atrix) theory, чтобы подчеркнуть связь с М-теорией.

Виттен не был первым, кто задумался о связи между одиннадцатимерной теорией и теорией струн. На протяжении нескольких лет ряд физиков пытались привлечь внимание теоретической общественности к одиннадцатимерной теории, содержащей мембраны. Майк Дафф из Техасского университета A&М (сейчас он работает в Имперском колледже Лондона) высказал бо́льшую часть идей несколькими годами раньше, но струнные теоретики не приняли их. Мембраны казались слишком сложными, математики недостаточно хорошо их понимали, чтобы принимать всерьёз те семена, которые Дафф пытался посеять в их умах. Но Виттен был авторитетом, и струнные теоретики, зацепившись за М-теорию, уже никогда больше не отпускали её.

Так что же это за М-теория, так захватившая воображение физиков? Это не теория струн. Неодномерные энергетические нити населяют её мир одиннадцати пространственно-временных измерений. Так почему же вдруг теоретики так заинтересовались двумерными энергетическими листами – мембранами, как они их назвали? Ответы на эти загадки лежат под покровом тайны компактификации.

Давайте вернёмся к бесконечному цилиндру и вспомним, как мы его получили. Мы начали с бесконечного листа бумаги и вырезали из него бесконечную полосу шириной в несколько сантиметров. Представьте, что края полосы – это пол и потолок двумерной комнаты. Комната огромна, она бесконечно простирается в направлении x, но в направлении y она ограничена снизу и сверху полом и потолком. На следующем этапе мы соединяем пол с потолком и получаем цилиндр.

Представьте частицу, летящую в упомянутой бесконечной комнате. В определённый момент частица сталкивается с потолком. Что произойдёт дальше? Если полоса свёрнута в цилиндр, не возникает никаких проблем: частица просто продолжит свой путь, проходя сквозь потолок и появляясь из пола. В действительности нам не обязательно сворачивать бумажную полосу в цилиндр: достаточно просто знать, что каждая точка потолка соответствует единственной точке пола, так что когда частица проходит через край, она мгновенно оказывается на другом краю. Мы можем свернуть полосу или оставить её плоской: нужно лишь следить за выполнением правила, согласно которому каждая точка потолка идентифицируется с точкой пола, находящейся с ней на одном перпендикуляре к краю.

Теперь давайте немного усложним картину: пусть теперь наша комната имеет три измерения, как реальная комната, за исключением того, что она бесконечно простирается в двух направлениях, на этот раз в направлении x и в направлении z. Но в вертикальном направлении y она по-прежнему ограничивается полом и потолком. Как и прежде, когда частица проходит сквозь потолок, она мгновенно появляется из пола. Трёхмерное пространство можно компактифицировать до двумерного. Если высоту комнаты, или, другими словами, расстояние вдоль оси y, сократить до микроскопических размеров, получившееся пространство будет восприниматься как двумерное.

Как я уже сказал, в М-теории нет струн, а есть только мембраны. Как совместить её с теорией струн? Представьте себе ленту, ширина которой в точности равна высоте комнаты. Поместим эту ленту в комнату так, чтобы её края касались пола и потолка. Сама лента при этом может иметь любую форму, она может змеиться вдоль комнаты, изгибаясь любым способом. Единственное условие состоит в том, чтобы эта поставленная на ребро лента всюду касалась пола и потолка и была в точности вертикальна. На самом деле лента больше не имеет края и в этом отношении подобна бумажному цилиндру. Но проще всего визуализировать её в виде длинной извилистой ленты, змеящейся по бесконечной комнате, пол и потолок которой соединены друг с другом описанным выше правилом.

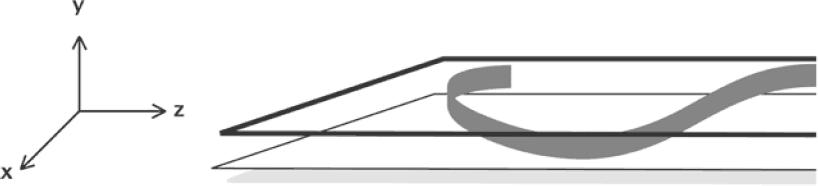
Теперь вы понимаете, как лента, представляющая собой двумерную мембрану, может имитировать одномерную струну. Если компактифицированное измерение настолько мало, что его невозможно увидеть без микроскопа, то для всех практических применений ленту можно считать струной. Если лента замкнута в кольцо, она будет неотличима от закрытой струны: струны типа IIa, если быть точным.

Такова связь между М-теорией и теорией струн. Струны на самом деле являются очень тонкими лентами, или мембранами, которые выглядят как тонкие струны, когда координата, представляющая их ширину, компактифицируется. Как видите, не так уж это и сложно.

Но можно пойти дальше и сделать ещё один шаг в сторону компактификации: компактифицируем теперь два измерения, скажем, z и y. Чтобы визуализировать этот процесс, представим себе не бесконечную комнату, а бесконечный коридор. У нас есть стены слева и справа, а также потолок и пол вверху и внизу. Но если смотреть вдоль коридора, то взгляд проникает сколь угодно далеко в любом направлении. Как и прежде, если объект пересекает потолок, он появляется из пола. Но что делать, если объект пересекает одну из стен? Вы, вероятно, уже знаете ответ: он появляется из противоположной стены, прямо напротив места, где он коснулся первой стены.

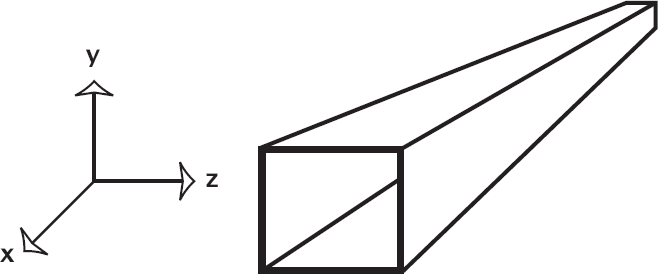
Точно тот же трюк может быть проделан и в десятимерном пространстве М-теории, только на этот раз «коридор» простирается на бесконечное расстояние в восьми из десяти пространственных направлений. Как и следовало ожидать, когда ширина и высота потолка становятся очень маленькими, неуклюжий крупномасштабный наблюдатель начинает считать, что он живёт в мире, состоящем из восьми пространственных измерений (плюс одно временно́е).

Тут-то и появляется на сцене шокирующее и странное следствие теории струн. Как только ширина и высота коридора становятся меньше определённого размера, из ниоткуда вырастает новое измерение. Это новое пространственное направление не является ни одним из тех, с которых мы начали. Мы знаем о нём благодаря косвенным математическим свидетельствам теории струн. Чем меньше мы делаем исходные пространственные измерения, тем бо́льшим становится новое. В конечном итоге, если уменьшить коридор до нулевой высоты и ширины, размер нового измерения станет бесконечным. Поразительным следствием компактификации двух пространственных измерений оказывается получение в итоге не восьми, а девяти несвёрнутых пространственных направлений. Этот весьма странный факт, что десять минус два равно девяти, является одним из неожиданных следствий теории струн. Геометрия пространства далеко не всегда такова, какой представлял её себе Евклид или даже Эйнштейн. Очевидно, что на малых расстояниях пространство отличается от чего бы то ни было, что физики и математики могли представить себе даже в самых смелых мечтах.

Возможно, вас слегка запутало, что я постоянно использую то название «теория струн», то «М-теория» в отношении, казалось бы, одних и тех же вещей. Струнные теоретики тоже постоянно путаются в терминологии. Например, можно ли считать одиннадцатимерную теорию, содержащую мембраны, но не содержащую струны, частью теории струн? А компактифицированная версия М-теории, в которой мембраны трансформируются в струны, – это по-прежнему М-теория? Я боюсь, что эта книга не очень подходящее место для терминологических дискуссий. Что касается меня, то я отношу к теории струн всё, что выросло из первоначальной теории струн, созданной много лет назад. Сюда входит и то, что сегодня называется М-теорией. Термин же «М-теория» я использую, когда хочу подчеркнуть, что речь идёт именно об одиннадцатимерной теории.

В главе 10 я продолжу рассказ о теории струн, а сейчас хочу взять тайм-аут и дать вам отдохнуть от сложных технических аспектов теории струн и поговорить о проблеме, которая касается каждого серьёзного физика. На самом деле она касается не только физиков, а вообще всех, кто заинтересован в понимании природы на самом глубоком уровне.