Израильско-американский психолог Амос Тверски, имевший рост 5 футов 9 дюймов, был страстным поклонником баскетбола. Он смотрел матчи, активно болел и сам играл с друзьями, причем весьма агрессивно. «Он был грубым на площадке, – рассказывала мне жена Тверски Барбара. – Приходил домой весь побитый. Я говорила ему, что баскетбол – бесконтактный вид спорта!»

Будучи болельщиком, Тверски знал о теории легкой руки. Убеждение, что существуют победные серии, широко распространено среди баскетболистов, тренеров, спортивных комментаторов и болельщиков. Причем не простых победных серий, а предсказуемых. Якобы у игрока, сделавшего несколько результативных бросков подряд, «легкая рука», или он находится «в зоне». Значит, в следующий раз он с большей вероятностью попадет в корзину, чем промахнется.

Это логично. Удачные броски повышают уверенность в себе, что само по себе хорошо. Успех порождает успех. Теория легкой руки вплетена в рассуждения спортивного комментатора и влияет на игровую стратегию. Игроки стараются передать мяч удачливому товарищу по команде: у него больше шансов отправить мяч в корзину. Команда соперников, наоборот, старается прервать пасы игроку с легкой рукой и блокировать его броски.

Многие болельщики считают теорию легкой руки само собой разумеющейся и не требующей доказательств. Просто понаблюдайте немного за игрой, и вы увидите сами. Игроки, сами оказывавшиеся «в зоне», тоже не сомневаются. Первис Шорт из команды Golden State Warriors однажды сказал:

Когда предлагается предъявить доказательства, зануды-болельщики начинают сыпать примерами победных серий. 8 декабря 1992 г. Доминик Уилкинс из клуба Atlanta Hawks сделал 23 результативных броска подряд. 22 января 2006 г. Коби Брайант принес клубу Los Angeles 81 очко в игре против Toronto. Оба случая считаются самыми яркими примерами легкой руки.

Тверски вел в Стэнфорде семинар. Он рассматривал эксперименты по имитации случайности. Один из его студентов, Томас Гилович, предложил выполнить исследование эффекта легкой руки. Он считал, что некая связь существует. Учитывая, что людям трудно придумывать случайные последовательности, можно предположить, что они также плохо понимают события, близкие к случайным, например, баскетбольные броски. Гилович предположил, что болельщики преувеличивают значение легкой руки.

«Я пошел к Амосу, чтобы поговорить об этом, – рассказывал Гилович, – и с удивлением обнаружил, что он заинтересовался». Однако Тверски настаивал, что полосы удач не существует. Это миф! В игре больше случайности, чем полагают болельщики.

«Он сказал, что по-настоящему проверить это нельзя, поскольку невозможно получить достаточно данных, – вспоминал Гилович. – За год, проведенный в Гарварде, он собрал лишь небольшой массив данных. И тогда я сказал, что смогу собрать достаточно информации, чтобы проверить эту идею».

Для этого Гиловичу требовалась полная запись попаданий и промахов, причем в их реальной последовательности. В то время только один клуб НБА вел такую статистику – Philadelphia 76ers. Их педантичный статистик Харви Поллак предоставил записи, и идея Гиловича легла в основу статьи. Другой студент, Роберт Валлоне, вызвался помочь со статистикой. Гилович, Валлоне и Тверски опубликовали результаты работы в журнале Cognitive Psychology в статье под названием «Легкая рука в баскетболе: О неправильном восприятии случайных последовательностей» (The Hot Hand in Basketball: On the Misperception of Random Sequences). Она вызвала споры, не утихающие до сих пор.

Статья посвящена не только баскетболу. Спорт становится поводом для обсуждения того, как наш мозг воспринимает окружающую смесь предсказуемого и случайного. Три автора с разных точек зрения анализируют теорию легкой руки. Они провели опрос среди игроков НБА и болельщиков из студенческой среды, спрашивая, повышается ли после удачного броска вероятность того, что игрок не промахнется и в следующий раз. Подавляющее большинство ответили утвердительно. Исследователи изучили записи бросков клубов Philadelphia 76ers и Boston Celtics (у них были данные бросков из-за трехочковой линии) и подвергли их статистическому анализу. Они также провели эксперименты с трехочковыми бросками среди мужских и женских команд Корнеллского университета, предлагая добровольцам делать ставки на легкую руку.

Во всех случаях свидетельств эффекта легкой руки обнаружено не было. Все верили в свою способность предсказать то, что на самом деле непредсказуемо (и ставили деньги).

В статье проводится важное разграничение между легкой рукой и полосой удач. Совершенно очевидно, что бывают случаи, когда игрок совершает необычно большое число метких бросков подряд благодаря – за неимением лучшего слова – удаче. Аналогичные полосы везения случаются в рулетке, в игре в кости и в лотерее. Разумные люди соглашаются: везение в рулетке непредсказуемо и зависит только от удачи.

Точно такое же разграничение психологи проводят между легкой рукой и талантом. Не подлежит сомнению, что одни спортсмены лучше играют в баскетбол, чем другие. Игрок с поставленным броском имеет больше шансов попасть в кольцо несколько раз подряд. Джулиус Ирвинг, бывшая звезда баскетбола, 52 процента всех очков набрал в сезоне 1981–82 гг. Можно сравнить это с результатом подбрасывания монетки со смещенным центром тяжести, с вероятностью выпадения орла 52 процента. Будет ли у доктора Джулиуса победных серий больше, чем серий орлов при подбрасывании монеты, и будут ли они длиннее? Если да, то это свидетельствует в пользу теории легкой руки. Иначе можно предположить, что победные серии Ирвинга – лишь проявление обычной случайности.

Исследования подтвердили последнее. Талант игрока определял общую вероятность попадания мяча в корзину, однако победные серии оказались не длиннее, чем можно было бы ожидать от случайности.

Вполне возможно, что игроки другой команды прилагали больше усилий для блокирования меткого баскетболиста, поскольку верили в легкую руку. Это может скомпенсировать эффект, который существует на самом деле. Чтобы проверить такую возможность, группа Гиловича организовала трехочковые броски среди команд Корнеллского университета. Соперники в данном случае отсутствовали, и никакая стратегия не вносила искажений в результат. Это был чистый тест теории легкой руки, и результат его оказался точно таким же. Легкая рука – иллюзия.

Тренер команды Celtics Ред Ауэобах был знаменит тем, что мог предсказать исход матча в середине игры. Убежденный, что его команда вышла на непобедимую серию, он закуривал сигару. Когда ему рассказали о статье, посвященной легкой руке, Ауэрбах спросил: «Да кто он такой? Ну, провел исследование, а мне какая разница?».

«В бросках по кольцу в баскетболе важно столько факторов, – говорил Бобби Найт, тренер Indiana Hoosiers, – что подобные статьи абсолютно ничего не значат».

Спортивный комментатор NCAA Билли Паркер посоветовал статистику «познакомиться с реальной жизнью».

С тех пор теория легкой руки подробно рассматривалась в литературе по психологии и статистике, в посвященных баскетболу блогах, в спортбарах, а иногда и в СМИ. Большое количество исследований подтвердили выводы GVT (аббревиатура фамилий Гиловича, Валлоне и Тверски). В 2011 г. вышла статья Тэла Неймана и Йонатана Левенштейна из Иерусалимского университета. Они анализировали броски с игры в мужской и женской американских баскетбольных лигах. Игрок, пытающийся забросить мяч в корзину с игры, может сделать это из двух зон, двухочковой и трехочковой; второй вариант сложнее. Решение зависит от уверенности в себе. Исследование показало: профессиональные баскетболисты после удачного трехочкового броска с большей вероятностью повторяли попытку. Возможно, верили в легкую руку. Коби Брайант, названный в сезоне 2007–08 гг. самым ценным игроком, после успешного трехочкового решался на следующий такой же бросок почти в четыре раза чаще, чем после промаха.

Но Брайант, подобно всем остальным, совершал ошибку, руководствуясь результатами своих действий. Нейман и Левенштейн показали, что вероятность меткого трехочкового броска после попадания в кольцо чуть меньше, чем после промаха – 36 процентов против 38 процентов.

Исследователи также обнаружили, что у игроков короткая память. Решение о попытке трехочкового броска принималось в основном по результатам последнего попадания. Предпоследний удачный бросок оказывал уже меньшее влияние, а всё, что произошло раньше, в буквальном смысле забывалось и никак не влияло на принятие решения. Выбор игроков НБА относительно броска был так же предсказуем, как выбор людей, игравших с машиной для предсказаний.

Вера в легкую руку (или ее отрицание) присутствует и во многих других видах спорта. Для этого даже придумали общий термин – серийность. Существует представление о большей, чем для случайных явлений, вероятности выигрышных или проигрышных серий в бейсболе, футболе, теннисе и гольфе – а если точнее, то в любом виде спорта, где ведется статистика. Серии применимы к отдельным игрокам и победным играм или сезонам; о сериях также говорят применительно к скачкам и собачьим бегам.

В настоящее время не подлежит сомнению, что легкая рука не всегда миф. По-настоящему легкая рука, похоже, проявлется в боулинге. Если игрок сбивает все десять кеглей первым броском (страйк), то получает десять очков плюс количество кеглей, сбитых за два последующих броска. Такая система мотивирует игрока стараться изо всех сил после страйка – и это помогает. Накопленные данные показывают: игроки в боулинг, осваивающие страйк, с немного большей вероятностью повторяют его или делают спэр (выбивают десять кеглей за два удара).

Существуют также свидетельства серийности в некоторых соревнованиях. Победа в теннисном матче требует выигрыша двух из трех сетов. Игрок, выигравший первый сет, может прибегнуть к прессингу по всему корту (если можно так выразиться), чтобы добиться победы на втором. То же самое относится к профессиональным гольфистам, когда от квалификации на вожделенный чемпионат их отделяют одна или две игры. Эффект легкой руки существует в индивидуальных видах спорта, где система отсчета поощряет следующие друг за другом победы. Командные виды спорта в большей степени случайны, и в них слишком много переменных, недоступных контролю отдельного человека.

Но сказанное не меняет ситуации: болельщики настроены видеть серийность там, где ее нет. Благодаря вирусному распространению через интернет вера в легкую руку в настоящее время только усилилась. Охваченные этой страстью блогеры по-прежнему яростно нападают на статью Гиловича, Валлоне и Тверски, написанную несколько десятилетий назад. «Когда вся ваша жизнь убеждает вас в чем-то, и вы на самом деле испытываете это, а затем вам говорят противоположное, то вы сопротивляетесь, – объяснял Гилович. – Я не имею в виду, что люди, верящие в легкую руку, подобны тем, кто считает, что земля плоская, но когда человек впервые заявил, что земля не плоская, это выглядело безумием».

Идея легкой руки – следствие непонимания природы ситуации, проявляющейся в экспериментах по имитации случайности. На самом деле группа Гиловича выполнила именно такой эксперимент, только новой разновидности. Они показали испытуемым последовательности из значков Х и О, и попросили определить, какая из них случайная, а какая нет. Участникам эксперимента также предлагалась легенда, что последовательности представляли собой запись попаданий и промахов при бросках в кольцо в баскетболе. Обе воспринимались как реальные данные.

Чтобы вы почувствовали это на собственном опыте, приведу пример полоски из белых и черных квадратов (ее легче воспринимать визуально, чем буквы). Представьте, что черные квадраты – это меткие броски в баскетбольную корзину, а белые – промахи:

В 1985 г. большинство людей согласились, что подобные последовательности случайны.

Это неудивительно – как и то, что они ошиблись. Вот как выглядит случайная последовательность:

В ней меньше чередований черного и белого, а также более длинные серии одного цвета, чем на первой диаграмме.

Суть случайности – непредсказуемость. Если вы – и все остальные – не в состоянии угадать, что будет дальше, значит, это случайное явление. Примером случайности может служить подбрасывание монеты. Вторая диаграмма представляет собой результат подбрасывания монеты 50 раз, где черные квадраты обозначают орла, а белые решку. Вероятность того, что за белым квадратом последует черный (или наоборот) составляет 50 процентов.

Но когда группа Гиловича показала испытуемым эту случайную последовательность, только 32 процента признали ее случайной. Большинство были убеждены, что ряды одинаковых символов слишком длинные, чтобы считать их совпадением. Это позволяет предположить, что легкая рука не просто спортивный миф, а универсальная иллюзия.

Психологи протестировали последовательности, в которых вероятность чередования составляла 40, 50, 60, 70, 80 и 90 процентов. Ощущение случайности было наибольшим при частоте чередований 70 или 80 процентов. В первой из приведенных выше диаграмм она составляет 75 процентов; это вероятность того, что за белым квадратом последует черный, и наоборот.

И только когда вероятность чередования увеличивается до 90 процентов, большинство людей считают, что чередование слишком ритмично, чтобы быть случайным. Вот пример последовательности с уровнем чередования 90 процентов:

Это почти идеальная последовательность черного и белого. Встречается только два повторения одного и того же цвета подряд, причем длина – всего два квадрата.

Как и во всех других случаях, фокусники использовали эти идеи задолго до того, как о них написали психологи. Иллюзионисты давно знали, что честно перетасованная колода карт рискует показаться зрителям не случайной. В ней обязательно попадутся «подозрительные» группы похожих карт, например, четыре картинки подряд. Статистику это не покажется странным – в отличие от обычного человека.

В некоторых фокусах используется колода, выглядящая лучше, чем действительно перетасованная. Карточный аналог последовательностей с избытком чередования, нами они воспринимаются как случайные. В так называемой раскладке Си Стеббинса карты чередуются в строгом порядке: черная-красная-черная-красная-черная-красная. Масти во всей колоде тоже разложены не случайно: трефы-червы-пики-бубны. Значения следуют в таком порядке: Т–4–7–10–K–3–6–9–Д–2–5–8–В. Может сложиться впечатление, что эти закономерности взяты с потолка. Ничего подобного. Колода только выглядит случайной.

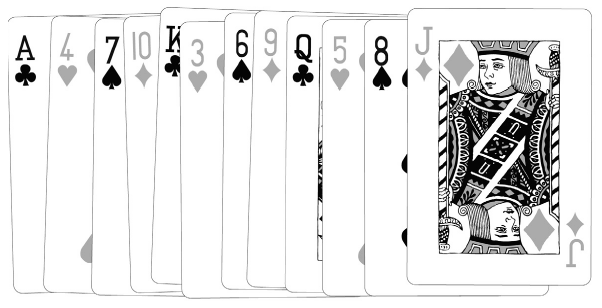
Раскладку Стеббинса запомнить просто, и в этом суть. Фокусник, видящий нижнюю карту снятой колоды, мгновенно вычисляет следующую… а она становится верхней картой вновь сложенной и выровненной колоды. При желании он может назвать эту карту, а также любую другую карту в колоде.

В большинстве случаев мы очень хорошо умеем обманывать сами себя. Поняв, что «легкая рука» – иллюзия, мы начинаем видеть ее примеры повсюду. Многие пользователи iPod жалуются, что функция воспроизведения в случайном порядке работает не так, как должна. Это не может быть случайным – только что плеер проиграл четыре песни Лил Уэйн подряд! Но такие серии должны встречаться. Дефект не в программе, а у нас в голове.

Расписание автобусов на оживленных улицах Манхэттена почти ничего не означает, потому что из-за плотного потока транспорта и многочисленных светофоров автобусы приходят практически в случайном порядке. Однако график движения совсем не выглядит случайным. Создается впечатление, что ты ждешь автобуса 20 минут, а затем сразу приходят два или три подряд.

Специалист по когнитивной психологии Стивен Пинкер сообщает об эксперименте. Добровольцы должны нажимать кнопку, услышав звуковой сигнал. Участники эксперимента знали, что сигналы будут поступать в случайном порядке. Они жаловались, что машина неисправна: «Сигналы приходят пачками. Вот так: бип-бип-бип-бип-бип… бип… бип-бип… бип-бип-бип-бип-бип». Они не понимали, как выглядит случайность, объясняет Пинкер.

Когда легкая рука проявляется в двух или трех пространственных измерениях, а не только в одном, временном, это называется иллюзией кластеризации. Во время воздушных налетов на Лондон ходили слухи, что немецкие бомбы не попадают в кварталы, где живут нацистские шпионы. Карты показывали группы попаданий в одни районы и ни одного попадания в другие. Британская разведка восприняла эти слухи достаточно серьезно, разделила карту Лондона на квадраты и тщательно следила, куда падают бомбы. В результате они пришли к выводу, что бомбы действительно падают случайно. Статистик Уильям Феллер заметил: «Нетренированному глазу случайность видится как регулярность или тенденция к образованию групп». Многие отказывались верить. Как спрашивал Чико Маркс : «Ты веришь мне или своим глазам?»

На первый взгляд вера в легкую руку противоречит более известному «заблуждению игрока». 18 августа 1913 г. в казино Монте-Карло «черное» выпало 26 раз подряд. Примерно после 15-го раза об этом стало известно всем посетителям. Игроки побросали карты и игральные кости, и у стола с рулеткой собралась целая толпа. Большинство желали поставить на «красное». Они верили, что после стольких «черных» подряд вероятность того, что в следующий раз выпадет «красное», выше обычной. Когда это убеждение опровергалось – после того, как вслед за остановкой колеса в очередной раз выпадало «черное» – многие удваивали ставку, убежденные, что в следующий раз вероятность «красного» еще выше.

Заблуждение игрока – это вера, что случайный результат, не выпавший в прошлом, с большей вероятностью случится в ближайшем будущем. Это обоснованное заблуждение («я давно уже должен выиграть!» – думает каждый неудачник), но все-таки заблуждение, побуждающее неудачников продолжать игру, не учась на ошибках. Будь у любителей азартных игр хотя бы инстинкт самосохранения, как у крыс, преодолевающих лабиринт, они бы поняли: когда я играю, ничего хорошего не происходит. Вместо этого они продолжают делать ставки и в ответ на проигрыш могут даже поднимать их. К сожалению, колесо рулетки не может знать, что именно эти люди должны выиграть. Шансы остаются прежними.

Вполне возможно, что вы уже запутались. Создается впечатление, что я утверждаю: люди верят в продолжение победных серий… за исключением случаев, когда они верят в прямо противоположное. Ничего подобного. Заблуждение игрока и теория легкой руки – две стороны одной медали. И то, и другое – следствие «закона малых чисел».

Это полушутливое правило сформулировали в 1971 г. Амос Тверски и Дэниел Канеман. Оно гласит:

Чтобы понять его смысл и оценить шутку, нужно знать, что такое «закон больших чисел». Это одна из главных формул вероятности. Когда я подбрасываю монету, то орел и решка не обязательно выпадут одинаковое число раз. Для этого потребуется очень длинный случайный процесс. Но если я бросаю монету большое количество раз, то пропорция орлов приближается к ожидаемой величине (50 процентов).

Закон больших чисел утверждает, что от очень маленькой выборки нельзя ожидать, что она будет отражать процесс в целом. Мы все об этом знаем и иногда шутим на эту тему (даже неспециалисты). Средняя американская семья состоит из 2,6 человека. Но кто мог бы себе представить такое в реальности?

Закон малых чисел Тверски и Канемана применим в области психологии. Он гласит, что мы безосновательно ждем от маленькой выборки отражения реальной ситуации. Если подбросить монету десять раз, то закон больших чисел свидетельствует о возможности получить смещенный результат, например, семь решек и три орла. Но люди думают иначе. Покажите им монетку, на их глазах семь раз из десяти упавшую решкой вверх, и большинство скажет, что с монетой что-то не так.

Я не утверждаю, что монета не может быть дефектной. Если из 1000 раз 700 выпал орел, то у монеты почти наверняка смещен центр тяжести. Но в семи из десяти нет ничего подозрительного, даже если это единственные данные.

Другими словами, мы ждем, что маленькая выборка будет похожа на персонажей телевизионного реалити-шоу: один увалень, одна глупая блондинка, один гей, один черный, один азиат и так далее. Они должны «представлять всю Америку». Но в так называемых реалити-шоу это делается намеренно. Случайная выборка из всего населения страны может оказаться смещенной в ту или иную сторону.

В статье, посвященной эффекту легкой руки, предлагается единая теория, описывающая как легкую руку, так и заблуждение игрока. Гилович, Валлоне и Тверски писали:

Что заставляет людей переходить от заблуждения игрока к теории легкой руки и наоборот? Столкнувшись с тем, что считается механическим и не подлежащим контролю со стороны человека, мы впадаем в заблуждение игрока. Но если задействована воля человека, мы предпочитаем верить в легкую руку.

Любитель азартных игр признает непредсказуемость маленького шарика, катящегося по колесу рулетки. И одновременно он верит в закон малых чисел. Единственный способ примирить эти два убеждения – вообразить Госпожу Удачу, притормаживающую колесо рулетки, чтобы после череды черных выпало красное, просто ради того, чтобы уравнять шансы. Это заблуждение игрока.

И наоборот, у баскетбольного болельщика нет причин верить в случайность игры. Ее ход определяется мастерством, стратегией и достижениями спортивной медицины (помимо удачи). Когда у игрока победная серия, нерепрезентативная в долговременном плане, просто поверить в загадочный эффект легкой руки.

В человеческой жизни вера в легкую руку, вероятно, играет бо́льшую роль, чем заблуждение игрока. Заблуждение игрока – это вера наивных людей, относящаяся в основном к оборудованию для азартных игр. Более информированные читатели могут презрительно фыркнуть при упоминании Госпожи Удачи, манипулирующей картами и игральными костями. Теория легкой руки применяется в отношении действий человека. И совсем не очевидно, что вера в легкую руку не имеет под собой оснований – и в баскетболе, и во всем остальном. Гилович не знал о ложности этого представления, пока не занялся исследованиями. Умные люди могут верить в легкую руку и на основании этой веры принимать важные решения.

Эта шутка может послужить хорошим введением к понятию эвристики репрезентативности. Канеман и Тверски придумали этот термин для описания тенденции верить, что ограниченный опыт отражает общую картину (эвристикой называют творческое, интуитивное мышление). Оптимист из шутки не имеет опыта падения с небоскребов, но уверен, что его короткий полет – пролетел 50 этажей целый и невредимый! – отражает уготованную ему судьбу.

Однажды Канеман и Тверски стали в шутку предсказывать будущую профессию маленьких детей своих знакомых. Бойко болтающий трехлетний малыш, говорили они, станет адвокатом, когда вырастет. Они понимали, что делают необоснованные предсказания, опираясь на недостаточные данные. К их немалому удивлению, окружающие соглашались относительно будущего каждого ребенка. Проанализировав это явление, Канеман и Тверски поняли, что их слова всего-навсего соответствовали стереотипам. Разговорчивый ребенок отражает стереотип об адвокате, и это верифицирует прогноз.

Но что в этом плохого? Ничего, пока вы принимаете предсказание за то, что оно есть на самом деле – за догадку, вряд ли верную, поскольку профессий множество и адвокатов среди взрослого населения страны сравнительно немного.

В известной статье, написанной в 1972 г., Канеман и Тверски утверждали: многие наши неформальные оценки вероятности основываются на репрезентативности. Они исследовали поведение людей, описывая гипотетические ситуации и предлагая оценить вероятность. Выяснилось, что люди ошибаются одинаково.

Один из сценариев выглядел так. В городе был проведен опрос всех семей с шестью детьми. Обнаружилось, что в 72 семьях с шестью детьми последовательность рождения девочек и мальчиков была следующей: девочка-мальчик-девочка-мальчик-мальчик-девочка (ДМДММД). Оцените, во скольких семьях последовательность рождения девочек и мальчиков была МДММММ.

Возможно, это напомнит вам эксперименты радиостанции Zenith (именно на эту аналогию указывали Канеман и Тверски). Если рождение мальчика или девочки определяется случаем, то все 64 возможные комбинации, от ДДДДДД до ММММММ равновероятны. Разумно было бы предположить, что количество семей с последовательностью рождений МДММММ будет таким же, как с последовательностью ДМДММД, то есть 72. Однако средняя оценка, данная испытуемыми, оказалась равной 30. Люди считали, что последовательность МДММММ должна быть менее распространенной, чем «лучше перетасованная» ДМДММД. Подобная интуиция руководила отгадками в эксперименте радиостанции Zenith.

Сталкиваясь с трудным вопросом, мы иногда игнорируем его и отвечаем на более легкий (посмотрите на политиков в телевизионном шоу). Подобная тактика чаще встречается в тех случаях, когда отвечающий полагает, что был задан «неправильный» вопрос, и за ним кроется нечто большее. Вероятно, именно это и происходило. Участники эксперимента знали: последовательность рождения мальчиков и девочек случайна, и, отвечая, хотели это подчеркнуть. Они отдавали предпочтение «хорошо перетасованному» варианту как обычной случайности.

Самый простой вывод на основании результатов эксперимента – что большинство плохо знает математику. Но гораздо важнее то, что мы все выносим интуитивные суждения о вероятности. Самые главные суждения связаны с действиями людей. Обычно их невозможно свести к чистой математике. Вместо этого мы судим о вероятности на основе соответствия стереотипам. Спортсмен или руководитель компании, добившийся успеха несколько раз подряд, соответствует стереотипу «победитель», а не стереотипам «везунчик» или «неудачник». Мы интуитивно считаем, что успех должен что-то означать, а победная серия непременно продолжится.

Остается вопрос, почему мы до такой степени предсказуемы и так плохо умеем предсказывать? Легче продемонстрировать, как работает наше сознание, чем объяснить почему. Одна из возможных причин заключается в том, что люди раз за разом воспроизводят неверное представление о случайности – точно так же, как домашняя собака лает в безуспешной попытке имитировать человеческую речь.

Растратчик, подделывающий бухгалтерские документы, может избегать последовательностей одинаковых цифр из ложного убеждения, что они не будут выглядеть случайными. Баскетбольный тренер может верить, что пять метких бросков подряд статистически более значимы, чем на самом деле. Вне всякого сомнения, людей посещают подобные мысли.

Однако этими представлениями дело не ограничивается. Ошибочными оказываются восприятие и интуиция, а не только осознанные убеждения. Возникает вопрос, почему эволюция сформировала наше мышление так, что мы делаем неточные предсказания.

Было высказано предположение, что эвристика репрезентативности имеет значение для выживания. Плеск воды и последующий шорох в кустах может означать, что крокодил хочет схватить ребенка… а может ничего не означать. В этой и других подобных ситуациях безопаснее предположить худшее и принять меры (иногда ненужные), чем отмахнуться от непредсказуемости жизни и ничего не делать.

Одно несомненно: непонимание людьми случайности имеет глубокие корни. Психолог Лола Лопес сравнивала ее с притчей о слепцах и слоне – с той существенной разницей, что, «в отличие от ситуации со слонами, никто вообще не видел, что такое случайность».

Первая половина этой книги рассказывает о прямых последствиях нашей неспособности к случайным действиям. По большей части мы имеем дело с теми, кто сам пытается предсказать наши действия. Мы предсказываем групповые предсказания. Такое предсказание второго порядка – основа рынков, где значения приписываются ставкам на результаты в спорте, недвижимости, акциям и многому другому.

В начале 1989 г. экономист Колин Ф. Камерер задался вопросом: «Имеет ли вера в легкую руку значение для экономики?» Он предположил, что имеет – на малоэффективных рынках, таких как рынок труда и рынок недвижимости. Компании могут слишком много платить за услуги «успешных» руководителей, а покупатели – переплатить за дом, если они уверены, что повышение цен продолжится. Сегодня почти никто не сомневается, что эти предположения оказались верными. За прошедшие годы сотни исследований подтвердили влияние теории легкой руки на реальный мир. Иногда можно «обставить рынок», просто сыграв против представления о легкой руке. В следующих главах я покажу, как это сделать.