Глава 11. Солдатская сказка

31 марта 159 6 года хворая французская аристократка, сухо кашляя – возможно, туберкулез, – родила своего третьего ребенка. Младенец оказался слабым и болезненным. Несколько дней спустя мать скончалась. Врачи предсказывали, что вскоре и чадо последует за родительницей. Отцу ребенка пришлось ох как не просто, однако он не сдался. Первые восемь лет он не выпускал сына из дома, почти все время держал в кровати, приставил к нему сиделку и сам заботился о нем со всей родительской любовью. Ребенок протянет пятьдесят три года, прежде чем его доконают слабые легкие. Так был спасен для мира один из его величайших философов, архитектор следующей математической революции – Рене Декарт.

Когда Декарту было восемь (некоторые говорят, десять), отец отправил его в Ла-Флеш, иезуитскую школу – тогда еще новую, но вскоре приобретшую знаменитость. Ректор школы позволял юному Декарту допоздна валяться в кровати, покуда ученик не готов был явиться на занятия. Неплохая привычка, если удается ее поддерживать, а у Декарта это получалось вплоть до последних месяцев жизни. Учился Декарт хорошо, но по окончании восьми школьных лет начал демонстрировать скептицизм, которым и прославился как философ: он пришел к убеждению, что все, чему его учили в Ла-Флеш, либо бесполезно, либо ошибочно. Вопреки этому осознанию он подчинился желанию отца и провел еще два года в бесполезной учебе, на сей раз – в соискании степени в юриспруденции.

Наконец Декарт забросил науку букв и переехал в Париж. Там он ночами вел светскую жизнь, а днем лежал в постели и изучал математику (приступая к занятиям, разумеется, после полудня). Математику он полюбил, и она даже время от времени приносила ему доход – Декарт применял ее за игровым столом. Однако довольно скоро Париж Декарту приелся.

Что делали молодые люди с некоторыми средствами во времена Декарта, если желали странствовать и искать приключений? Шли в армию. В случае Декарта – в армию принца Морица Оранского (Нассауского). То была настоящая добровольческая армия – Декарту за его службу не платили. В итоге все остались при своих: Декарт не только ни в каких военных действиях не поучаствовал – через год он присоединился к вооруженным силам противника, герцога Баварии. Странное дело: сначала вербуемся к одним и не воюем, потом к другим – и опять не воюем. Но в тот период в войне Франции и Голландии против Испано-австрийской монархии возникло затишье, а Декарт пошел в армию ради путешествий, а не из политических соображений.

Служить Декарту понравилось: он встречался с людьми из разных краев, и в то же время ему хватало уединения, чтобы посвящать его изучению математики и наук, а также размышлениям о природе Вселенной. Его странствия почти немедленно принесли плоды.

Однажды в 1618 году солдат Декарт оказался в маленьком голландском городке Бреда, где увидел толпу, собравшуюся вокруг уличного объявления. Он подошел ближе и попросил пожилого зеваку перевести ему написанное на французский. Ныне в таком объявлении можно прочесть что угодно – рекламное воззвание, запрет парковки, призыв помочь с поисками человека. Но есть такое, чего теперь в уличных объявлениях не встретишь, а именно: математическую задачку, адресованную широкой публике.

Декарт осмыслил поставленную задачу и отметил походя, что она довольно проста. Его переводчик – может, озлившись на него, а может, забавы ради – взял незнакомца на слабо и принялся подначивать: дескать, давай, реши-ка. И Декарт решил. Пожилой собеседник ученого, человек по имени Исаак Бекман, сильно изумился, что само по себе целое дело: Бекман был выдающимся голландским математиком своего времени.

Бекман и Декарт так подружились, что Декарт впоследствии писал о Бекмане как о «вдохновителе и духовном отце» его учений. Именно Бекману Декарт четыре месяца спустя описал свои революционные взгляды на геометрию. Письма Декарта другу в следующие пару лет обильно приправлены отсылками к новым представлениям об отношениях между числами и пространством.

Всю свою жизнь Декарт относился к работам греков весьма критически, однако геометрия раздражала его пуще прочего. Она казалась ему неуклюжей и усложненной без всякой необходимости. Ему, казалось, противны были сами формулировки греческой геометрии, вынуждавшие его трудиться прилежнее потребного. Анализируя задачу, поставленную греком Паппом Александрийским, Декарт писал, что «мне утомительно уже то, сколько всего об этом надо писать». Он критиковал их систему доказательств, потому что каждое новое оказывалось уникальным в своем роде, и одолеть его можно было «лишь при условии великого изнурения воображения». Не одобрял он и того, как греки определяли кривые – описательно, что само по себе, конечно, бывало скучным, а доказательства делало путаными. Ныне ученые пишут, что «декартова математическая лень – притча во языцех», но самому Декарту вовсе не совестно было искать некую связующую систему, что упростила бы доказательства геометрических теорем. Таким способом он мог спать дольше и все равно больше сделать для науки, чем критиковавшие его более прилежные ученые.

Сравним для примера определение круга Евклидом (часть I «Начал») и Декартом – и убедимся в успехах последнего:

Евклид: Круг есть плоская фигура, содержащаяся внутри одной линии [которая называется окружностью], на которую все из одной точки внутри фигуры падающие [на окружность круга] прямые равны между собой.

Декарт: Круг есть все х и у, удовлетворяющие уравнению х² + у² = r² для заданного значения r.

Даже тем, кто не в курсе, что такое «уравнение», определение Декарта должно показаться проще. И вся штука не в том, чтобы определить, что такое уравнение, а в том, что в декартовом методе круг определяется им. Декарт перевел язык пространства на язык чисел и, что еще важнее, применил этот перевод к перефразированию геометрии в алгебру.

Декарт начал свой анализ с превращения плоскости в подобие графика, изобразив горизонтальную прямую и назвав ее осью х, а вертикальную – осью у. За исключением одной существенной детали, любая точка на этой плоскости описывалась теперь двумя числами: вертикальным расстоянием до горизонтальной оси, обозначенным у, и горизонтальным расстоянием до вертикальной оси, обозначенным х. Точки на плоскости с тех пор записываются в виде «упорядоченных пар» (х; у).

Но вернемся к существенной детали: если буквально отмерить расстояния, как описано выше, для каждой пары координат (х; у) найдется более одной точки. Например, рассмотрим две точки, каждая из которых на единичный отрезок выше оси х, но располагаются они по обе стороны от оси у: допустим, одна лежит на два единичных отрезка правее, а другая – на два единичных отрезка левее. Поскольку обе точки расположены на один единичный отрезок выше оси х и обе – в двух единичных отрезках от оси у, в соответствии с нашим рассуждением обе можно описать парой координат (2, 1).

Такая же неоднозначность возникает в почтовых адресах. Могут ли два человека, проживающие по адресу 80-я улица, 137, задрать нос и заявить: «Да я б никогда в том районе жить не стал». Отчего бы и нет? «Вестсайдская история» и «Истсайдская история» – однозначно две разные истории. Математики избавляются от этой неоднозначности в координатах в точности так же, как градостроители – в почтовых адресах, с той лишь разницей, что первые используют знаки «плюс» и «минус», а вторые приписывают к адресу «восточный»/«западный» или «северный»/«южный». Математики подрисовывают знак «минус» к координате х всех точек, размещающихся левее оси у (т. е. «восточной стороне» – «истсайду»), и к координате у всех точек, расположенных ниже оси х (т. е. «южной стороне», или «саутсайду»). В нашем случае у первой точки координаты останутся без изменений – (2, 1), а у второй станут такие: (– 2, 1). Мы делим плоскость на четыре четверти (квадранта) – северо-восточная, северозападная, юго-восточная и юго-западная. У всех точек в «южном» квадранте значение координаты у отрицательное, а у всех точек в «западном» отрицательно значение координаты х. Эту систему обозначения принято называть декартовыми координатами. (На самом деле примерно тогда же аналогичное открытие сделал Пьер Ферма, однако если за Декартом водилась дурная привычка ни на кого не ссылаться в своих публикациях, Ферма имел худшую склонность – не публиковать свои работы вообще.)

Ясное дело – и мы в этом уже убедились – применения координат как таковых новинкой не было. Птолемей еще во II веке использовал систему координат в своих картах. Но работы Птолемея сводились исключительно к географии. Никакого другого значения – помимо приложимости к земному шару – он в них не видел. Подлинное новаторство идей Декарта применительно к координатам состояло не в них самих, а в том, что́ Декарту удалось из них извлечь.

Изучая классические греческие кривые, манеру определения которых Декарт столь глубоко презирал, он, тем не менее, обнаружил удивительные закономерности. Например, он изобразил несколько прямых и выяснил, что для любой прямой координаты х и у любой точки на ней всегда связаны простым отношением. Алгебраически эту связь можно выразить уравнением вида ах + by + c = 0, где а, b и с – постоянные, т. е. обычные числа вроде 3 или 4¹/₂, и зависят они лишь от того, какую прямую в данный момент мы рассматриваем. Это означает, что любая точка, описываемая координатами (х, у), лежит на некоторой прямой тогда и только тогда, когда сумма х, взятого а раз, у, взятого b раз, и с равна нулю. Таково альтернативное – алгебраическое – определение прямой.

С точки зрения Декарта, линия есть множество точек с особым свойством: если прирастить одну координату, чтобы получить другую точку того же множества, необходимо прирастить и другую координату в строго заданной пропорции. Его определение круга (или эллипса) устроено по тому же принципу. С единственной разницей: убавляя одну координату, необходимо добавлять к другой так, чтобы (взвешенная) сумма квадратов координат, а не просто координат самих по себе, оставалась неизменной.

За триста лет до Декарта Николай Орезмский тоже подметил, что кривые можно определять через соотношение координат, и тоже вывел некоторое подобие уравнения прямой. Но во времена Орема алгебра еще не имела широкого хождения, и за отсутствием подходящей формы записи Орем не смог развить идею дальше. Декартов метод ассоциирования алгебры и геометрии привел к обобщению представлений Николая Орезмского, и теперь всю греческую математику можно было описать просто и сжато. Эллипсы, гиперболы, параболы – все их, как выяснилось, можно определить через простые уравнения в координатах х – у.

Возможность определять классы кривых по виду их уравнений имеет далеко идущие последствия для науки. Взглянем еще раз, к примеру, на данные, полученные Николаем, но сдвинем запятую в числах на один десятичный знак. Теперь-то понятно, что они такое – это таблица приблизительных средневысоких температур 15-го числа каждого месяца (кроме января) в Нью-Йорке. Ученый может задаться вопросом: есть ли простая взаимосвязь между этими показателями?

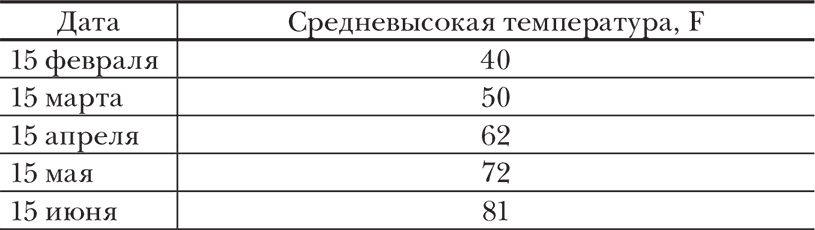
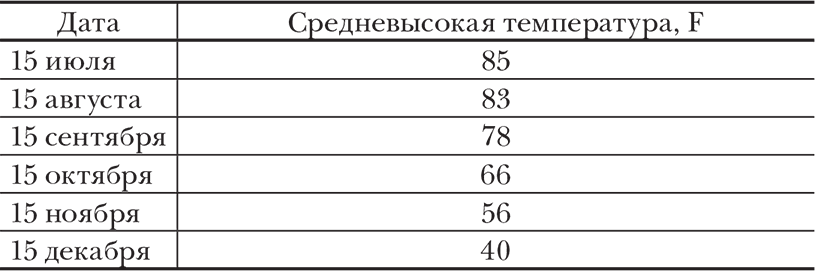
Как мы уже видели, отображение этих данных в виде графика дает нам простую геометрическую фигуру – параболу. Знание уравнения, описывающего параболу, дает нам кое-какие предсказательные возможности – позволяет сформулировать «закон средневысоких» для нью-йоркской погоды. Закон таков: обозначим через у температуру ниже 85 градусов по Фаренгейту, а через х – число месяцев до или после 15 июля, и тогда у равен дважды х в квадрате.

Опробуем это правило. Чтобы определить, какова будет средневысокая температура в Нью-Йорке, скажем, 15 октября, отметим, что октябрь – через три месяца после июля, т. е. х = 3. Поскольку три в квадрате – девять, средняя температура 15 октября есть дважды по девять, т. е. на 18 градусов ниже показателя 15 июля (85 градусов). Таким образом, по нашему «закону» выходит средняя температура приблизительно 67 градусов. Реальные данные – 66 градусов. Для большинства месяцев закон приложим вполне точно – и его можно применять и для других дней календаря, а не только к 15-м числам месяцев, если вам не лень возиться с дробями.

Сформулированный нами закон определяет отношение между у и х; это частный случай того, что математики называют функцией. В нашем примере парабола есть график функции. Физика в существенной степени занимается именно тем, что мы сейчас проделали: обнаружением закономерностей в данных, определением функциональных зависимостей и (этим мы не озаботились) объяснением причин той или иной взаимосвязи.

Точно так же, как можно вывести физические законы графически, применив картезианские методы, у евклидовых теорем тоже есть алгебраические следствия. Например, представьте теорему Пифагора в декартовых терминах. Вообразите прямоугольный треугольник. Для простоты положим, что вертикальная сторона его лежит вдоль оси у и тянется от точки начала координат до точки А, а горизонтальная сторона – из точки начала координат вдоль оси х до точки В. Таким образом длина вертикальной стороны равна координате у ее конечной точки А, а длина горизонтальной стороны – координате х конечной точки В.

Теорема Пифагора в данном случае говорит нам, что сумма квадратов горизонтальной и вертикальной сторон, х² + у², есть квадрат длины гипотенузы. Если принять определение, что расстояние между двумя точками А и В есть длина линии, соединяющей их, то мы только что установили, что квадрат расстояния между А и В есть х² + у². А теперь представим любые две точки А и В на плоскости. Мы вполне можем изобразить оси х и у так, чтобы получилась та же ситуация, которую мы только что рассмотрели: А размещается на горизонтальной оси, а В – на вертикальной. Это означает, что квадрат расстояния между любыми двумя точками А и В есть попросту сумма квадратов разниц между их соответствующими координатами.

* * *

Декартова формула для определения расстояния имеет глубокие связи с евклидовой геометрией, и нам еще предстоит в этом убедиться. Но его представление о расстояниях как о функции разниц координат и в общем случае состоятельно; именно оно позднее стало ключевым для понимания природы и евклидовой, и неевклидовой геометрий.

Декарт применил свои прозрения в геометрии ко многим своим знаменитым трудам в физике. Он первым сформулировал закон рефракции света в его современном тригонометрическом виде; ему же принадлежит первое исчерпывающее объяснение физики радуги. Его геометрические методы оказались настолько всеобъемлющими для всех его представлений, что он сам писал: «Вся моя физика есть не что иное как геометрия». И тем не менее Декарт откладывал издание своих трудов по геометрии координат целых девятнадцать лет, да и вообще ничего не публиковал до своих сорока. Чего он боялся? Да как обычно – Католической церкви.

По многократному настоянию друзей Декарт уже готов был обнародовать свои работы несколькими годами ранее – в 1633-м. И тут этот итальянец по имени Галилей издал труд под названием «Диалог о двух главнейших системах мира». Симпатичная такая пьеска – трое болтунов разговаривают об астрономии. Явно внебродвейское нечто. Но почему-то отцы Церкви решили разобраться, что к чему, и как-то не впечатлились. Быть может, сочли, что актер, представлявший их птолемеевские воззрения, получил слишком мало реплик. К сожалению, в те дни, если Церковь бралась рецензировать книгу, она рецензировала и автора, а результатом такой рецензии – и для книги, и для автора – мог стать костер. В случае с Галилеем сожгли книгу, а самому Галилею пришлось от нее отречься и – ах да! – от Инквизиции ему еще и достался тюремный срок без возможности откинуться. Декарт фанатом Галилея не был. Он даже написал свою рецензию на книгу итальянца: «Сдается мне, ему [Галилею] не достает вот чего: он постоянно отвлекается и все никак не раскроет во всей полноте ту или иную тему, а это говорит о том, что он в ней не разобрался по порядку…» И все же он разделял гелиоцентрические представления Галилея, а также и другие разумные соображения, и потому принял тяжкую участь Галилео близко к сердцу. Хоть он и жил в протестантской стране, издание своей книги все равно отменил.

Но все-таки Декарт наконец собрался с духом и в 1637 году обнародовал первую работу, позаботившись о том, чтобы его труд никоим образом не задевал Церковь. К сорока годам Декарту было что сказать далеко не только о геометрии, и он объединил все накопившееся одном томе. Под предисловие потребовалось 78 страниц. Оригинальная рукопись носила не слишком хлесткое название: «Рассужденье о вселенской науке, что могла бы возвысить нашу природу до величайших вершин совершенства; далее о диоптрике, о метеорах и геометрии, где любопытнейшие соображения, какие автор смог добыть, дабы доказать вселенскую науку, кою он предлагает, объясняются таким манером, что даже и те, кто никогда не учился, смогут их постичь». При издании название слегка подсократили – видимо, сотрудники той службы, что в XVII веке выполняла функции отдела издательского маркетинга. И все равно получилось длинновато. Время обточило название до совсем краткого, и ныне эту работу Декарта обычно именуют «Рассуждением» или «Рассуждением о методе».

«Рассуждение о методе» – протяженный трактат, описывающий философию Декарта и его рациональный подход к решению научных задач. «Геометрия», третье приложение, была призвана показать результаты, каких удалось добиться методами, предложенными Декартом. Свое имя он с титульного листа убрал – и не потому, что название заняло всю страницу, а из-за неизбывной боязни преследования. К сожалению, его друг Марен Мерсенн написал вступление и в нем не оставил никаких сомнений в личности автора книги.

Опасения Декарта оправдались: его подвергли жестокой критике – за брошенный Церкви вызов. Даже математическая часть его труда вызвала злобную реакцию. Ферма, который, как мы уже сказали, открыл сходный способ алгебраизации геометрии, взялся цепляться по мелочам. Блез Паскаль, другой гениальный французский математик, отверг работу целиком. И все же частные распри лишь ненадолго могут удержать развитие науки, и всего через несколько лет декартова геометрия стала частью практически любого университетского курса. А вот философию его принимать не торопились.

Яростнее прочих на Декарта нападал человек по имени Воэций – глава богословского факультета Университета Утрехта. Ересь Декарта, по мнению Воэция, была обычного сорта: вера в разум и наблюдение как инструменты определения истины. Декарт же на самом деле пошел еще дальше – он верил, что люди могут властвовать над природой, а также совсем скоро обнаружат лекарства от всех болезней и тайну вечной жизни.

Декарт мало с кем дружил и так и не женился. Любовь же у него все-таки была, ее звали Элен. В 1635 году она родила ему дочку – Франсин. Судя по всему, они прожили втроем с 1637 по 1640 год. Осенью 1640-го, в разгар войны с Воэцием, Декарт уехал приглядеть за изданием своей новой книги. Франсин заболела – вся покрылась багровыми пятнами. Декарт поспешил домой. Нам не ведомо, успел ли он вовремя, но девочка умерла на третий день болезни. Декарт и Элен вскоре расстались. Если бы не запись, рассказывающая о ее жизни и смерти, сделанная на клапане обложки одной из книг Декарта, мы бы, может, никогда и не узнали, что Франсин была его дочкой, а не племянницей, как он всем говорил – во избежание скандала. Декарт всю свою жизнь был известен как человек безэмоциональный, а эта смерть раздавила его. После нее он не прожил и десяти лет.