Глава 17. Блуждания в гиперболическом пространстве

Что же за птица это неевклидово пространство? Гиперболическое пространство, открытое Гауссом, Бойяи и Лобачевским получается, если заменить постулат параллельности допущением, что для любой данной прямой есть не одна, а несколько параллельных прямых, проведенных через ту или иную точку, не лежащую на данной прямой. Одним из следствий этого, писал Гаусс Тауринусу, является то, что сумма всех углов в треугольнике всегда меньше 180° на величину, которую Гаусс назвал угловым дефектом. На другое следствие наткнулся Валлис: подобных треугольников в таком пространстве не существует. Эти два следствия связаны между собой, поскольку угловой дефект зависит то размеров треугольника. Чем больше треугольник, тем больше угловой дефект, а маленькие треугольники – более евклидовы. В гиперболическом пространстве к евклидовым формам можно приблизиться, но достигнуть их нельзя – в точности как вы не достигнете скорости света или своего идеального веса.

Вроде бы малое изменение простой аксиомы – постулата параллельности, однако его хватило, чтобы породить волну, прокатившуюся по всему корпусу евклидовых теорем и поменявшую каждую, что описывала форму пространства. Словно Гаусс вынул стекло из евклидова окна и заменил его на искажающую линзу.

Ни Гауссу, ни Лобачевскому, ни Бойяи не удалось выработать простой способ наглядно иллюстрировать этот новый вид пространства. Это получилось у Эудженио Бельтрами и – попроще – у Анри Пуанкаре, математика, физика, философа и двоюродного брата будущего президента Франции Раймона. И тогда, и ныне Анри – менее известный Пуанкаре, но, как и его кузен, умел ввернуть словцо. «Математиками рождаются, а не становятся», – писал Пуанкаре. Так родилось это клише, и Анри прочно закрепил за собой место в народном сознании. А вот труд Анри 1880 года куда менее известен вне академических кругов – в этой работе он определил четкую модель гиперболического пространства.

Создавая свою модель, Пуанкаре заменил базовые элементы типа прямой и плоскости вещественными объектами, после чего перевел аксиомы гиперболической геометрии в эти новые термины. Допустимо переводить неопределенные термины пространства как кривые или поверхности – или даже как разновидности еды, если при этом смысл, который им сообщается применимыми к ним постулатами, хорошенько определен и непротиворечив. Можно смоделировать неевклидову плоскость как поверхность зебры, считать волосяные луковицы на ее шкуре точками, а полосы – линиями, если нам так хочется, покуда такой перевод не противоречит аксиомам. Например, вспомним первый постулат Евклида применительно к пространству зебры:

1. От всякой волосяной луковицы до всякой волосяной луковицы можно провести кусок полосы.

Этот постулат в пространстве зебры недействителен: у полос зебры есть ширина, и полосы эти размещаются на животном в строго определенном направлении. Между двумя волосяными луковицами, расположенными вдоль какой-нибудь полосы, но смещенными от нее в стороны, не получится провести кусок полосы. Зебр в модели Пуанкаре не было. Зато она была похожа на блин.

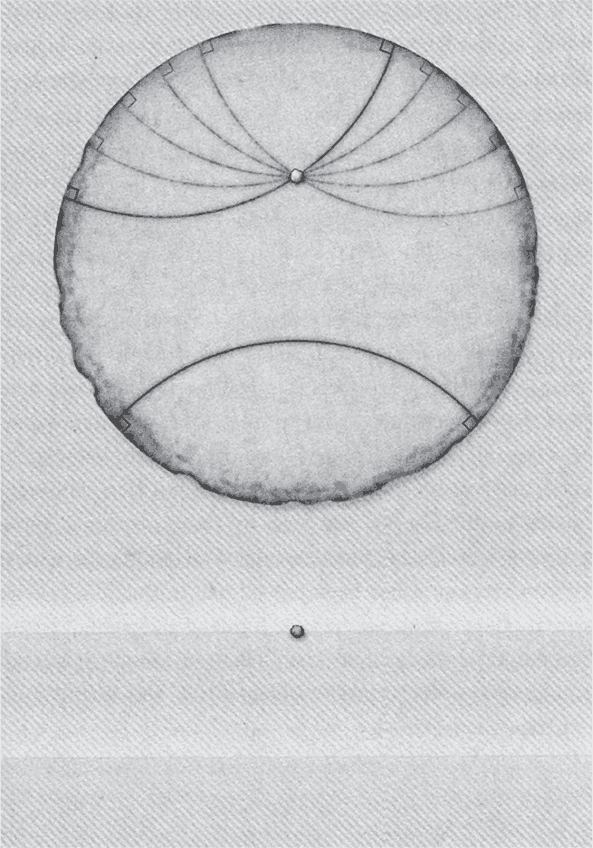
Вот как устроена Вселенная Пуанкаре: вместо бесконечной плоскости – конечный диск, вроде блина, но бесконечно тонкий и с идеальной круговой кромкой. «Точки» – такие штуки, которые считались точками со времен Декарта: местоположения, вроде кристалликов мелкого белого сахара. Линии Пуанкаре – вроде изогнутых бурых следов от сковородки. Если же говорить технически, эти линии – «любые дуги окружностей, пересекающие границу диска под прямыми углами». Чтобы не путать их с линиями, которые нам подсказывает интуиция, станем называть их линиями Пуанкаре.

Собрав эту физическую картинку, Пуанкаре должен был придать смысл применимым к ней геометрическим понятиям. Одним из важнейших оказалась конгруэнтность – то самое докучливое свойство фигур, которое Евклид предписал нам проверять путем наложения. В своем четвертом «общем замечании» Евклид писал:

4. И совмещающиеся друг с другом равны между собой.

Как мы уже говорили, возможность перемещать фигуры в пространстве, не искажая их, нам гарантирована лишь при условии принятия евклидовой формы постулата параллельности. Поэтому применение общего замечания № 4 в рецепте конгруэнтности – ни-ни в неевклидовом пространстве. Решение Пуанкаре – интерпретировать конгруэнтность путем определения системы измерения длин и углов. Две фигуры в таком случае окажутся конгруэнтными, если длины их сторон и углы между ними совпадут. Вроде очевидно, да? Но все не так-то просто.

Определение способа измерения углов оказалось вполне лобовым. Пуанкаре определил угол между двумя линиями Пуанкаре как угол между их касательными в точке пересечения этих линий. А вот чтобы ввести определение длин – или расстояний, – Пуанкаре пришлось попотеть. С постижением этого понятия могут возникнуть трудности, поскольку Пуанкаре запихнул бесконечную плоскость в конечную область. Например, вспомним второй постулат:

2. Ограниченную прямую можно непрерывно продолжать по прямой.

Очевидно, применение обычного определения расстояний к блину делает постулат недействительным. Но Пуанкаре переопределил расстояние: новое пространство сжимается по мере приближения к его краям, и именно так конечная область превращается в бесконечную. На первый взгляд все просто, но Пуанкаре не мог просто взять и определить расстояние по своему произволу – чтобы стать приемлемым, его определение должно было удовлетворять многим требованиям. Например, расстояние между двумя точками должно быть всегда больше нуля. Кроме того, в точном математическом выражении, выбранном Пуанкаре, линия Пуанкаре должна была соединять любые две точки по кратчайшей траектории, возможной между ними (такие линии называются геодезическими): в точности как обычные линии есть кратчайший путь между двумя точками в евклидовом пространстве.

Если вдуматься во все фундаментальные геометрические понятия, необходимые для определения гиперболического пространства, выяснится, что модель Пуанкаре приводит к непротиворечивому определению каждого. Мы можем проверить остальные, но интереснее всего рассмотреть именно постулат параллельности. Гиперболическая версия его, данная в модели Пуанкаре в форме аксиомы Плейфэра, выглядит так:

В плоскости через точку, не лежащую на данной линии Пуанкаре, можно провести множество других линий Пуанкаре, не пересекающих данную.

Рисунок на странице 179 иллюстрирует, как это выглядит.

Модель Пуанкаре для гиперболического пространства – лаборатория, где легко разобраться с кое-какими необычными теоремами и свойствами, которые математики с таким трудом пытались обнаружить. Предположим, например, что надо изобразить прямоугольник, не существующий в неевклидовом пространстве. Начертим для начала линию Пуанкаре в качестве базовой. Затем – еще два отрезка линий Пуанкаре, по одну и ту же сторону от базовой и перпендикулярные ей. Наконец соединим два отрезка третьим так, чтобы он, как и базовая линия, был перпендикулярен этим двум отрезкам. Это невозможно. В мире Пуанкаре не бывает прямоугольников.

Чего же Пуанкаре добился всем этим? Воображение рисует нескольких очкастых математиков Парижского университета: они по окончании семинара о модели Пуанкаре из вежливости аплодируют умнику Анри. Быть может, они даже приглашают Пуанкаре после его лекции на абсент или блинчик, на котором потом рисуют вареньем прямоугольники. Но зачем кому бы то ни было через сто с лишним лет писать книгу обо всем этом? Или вам – умному и очень занятому читателю – разбираться в ней?

Соль шутки вот в чем: модель Пуанкаре – не просто модель гиперболического пространства. Это и есть гиперболическое пространство (в двух измерениях). На языке математики это означает, что ученые доказали: все мыслимые математические описания гиперболической плоскости – изоморфны, или, говоря нашим с вами языком, одинаковы. Если наше пространство гиперболическое, оно поведет себя в точности как модель Пуанкаре (но только в трех измерениях). Перефразируя диснеевскую песенку, он вообще-то мал, этот блин.

Параллельные линии в гиперболическом и евклидовом пространствах

* * *

Через пару десятилетий после открытия гиперболического была открыта еще одна разновидность неевклидова пространства – эллиптическое. Оно получается при другом нарушении постулата параллельности: не существует никаких параллельных линий (т. е. все линии на плоскости должны пересекаться). В двух измерениях этот тип пространства был известен и в другом контексте изучен еще греками, а потом и Гауссом – но ни те, ни другой так и не прониклись важностью этого примера эллиптического пространства. Оно и понятно: в пределах евклидовой системы было доказано, что даже с допущениями альтернативных формулировок постулата параллельности эллиптических пространств не существует. В конце концов загвоздка заключалась не в самих эллиптических пространствах, а в аксиоматической структуре Евклида.