Пятый день
Задача 5
Расположите блоки в следующем порядке:
один из блоков должен касаться лишь одного другого;
один – двух других;
один – трех;
один – четырех;
один – пяти остальных.
Эта задача кажется более сложной, чем предыдущая. На самом же деле в ней меньше условий, поскольку ограничения установлены лишь для пяти блоков. Главное отличие здесь – для каждого блока они формулируются отдельно. Вам предстоит узнать, усложняет это задачу или нет.
На первый взгляд, задача подходит для поэтапного решения. Многие люди чаще всего пользуются именно этим методом. Условия задачи удовлетворяются одно за другим, а когда и последнее требование выполнено, задача может считаться решенной. Если подобных требований очень много, то есть задача кажется вам сложной, этот метод особенно эффективен. Хотя, возможно, вы предпочтете другой подход, не расчленяя задачу на части, а пытаясь упростить ее в рамках единого целого.
Недостаток поэтапного решения заключается в том, что многие задачи нельзя решить «по кусочкам». Если все части решения взаимосвязаны, нельзя получить нужный ответ шаг за шагом. Задачи с банками относятся именно к таким.
Другой недостаток рассматриваемого метода: выбор этапов может стать решающим. Неверный их порядок значительно усложняет решение задачи либо делает его невозможным. Выбор верной последовательности действий не всегда является очевидным.
Вместо поэтапного решения можно попытаться упростить задачу. Как? Рассмотреть задачу со всех сторон, пока не выявится в полной мере ее суть.
Задача 5 не связана с предыдущими. Опыт их решения здесь бесполезен.
Решение задачи 5
Ниже приведены возможные шаги при использовании поэтапного метода.
Первое требование: один блок должен касаться лишь одного другого.
Первый шаг: положите на стол один блок и придвиньте к нему второй.
Второе требование: один блок должен касаться двух других.
Второй шаг: придвиньте к ним третий блок соответствующим образом.
К сожалению, при выполнении второго требования мы нарушили первое. Такие недоразумения возникают довольно часто. Возможно, на этот раз вам удалось их избежать, но вы не застрахованы от них в будущем.
Другой путь поэтапного решения – оперирование поначалу не шестью, а тремя блоками. На этом этапе задача заключается в поиске комбинации блоков, в которой один из них имеет два контакта с другими. Ответ очевиден: нужно расположить блоки в ряд, где центральный блок контактирует с двумя, а крайний – с одним блоком. Следующая стадия: добавить четвертый блок так, чтобы число контактов для отдельных блоков составляло 1, 2 и 3. Этого легко достичь (рис. 18). Затем необходимо добавить пятый блок так, чтобы один из блоков имел четыре контакта с другими. Решение для этого этапа изображено на рис. 19. И, наконец, последний этап – размещение шестого блока с пятью контактами. Решение здесь можно получить столь же легко, как и на предыдущих этапах. Окончательное решение изображено на рис. 20. Лишь при таком методичном подходе задача не кажется чрезмерно сложной.
Вместо поэтапного метода вы могли прибегнуть к преобразованию предыдущих решений. Один из весьма интересных способов состоит в использовании решения задачи 4 (см. рис. 17) с модификацией его «методом вычитания». Так как в этой комбинации каждый блок касается пяти других, то идея заключается в уменьшении числа контактов отдельных блоков последовательно, пока оно не составит 1, 2, 3, 4 и 5. Сначала снимем один из верхних блоков и приставим его к одиночному нижнему. Теперь этот нижний блок будет по-прежнему касаться пяти, а остальные – четырех других блоков. Затем снимем один верхний блок и разместим его так, чтобы у блока с пятью контактами их число не изменилось, как и у одного из блоков с четырьмя контактами. Количество контактов оставшегося верхнего блока будет равно трем. Перемещенные вниз блоки имеют один и два контакта соответственно. Задача решена. Окончательная комбинация блоков показана на рис. 21. В ней последний верхний блок слегка повернут. Итак, посредством перемещения всего двух блоков решение задачи 4 превращается в решение задачи 5.
Возможны и другие пути решения этой задачи. Для вас представляет интерес проанализировать выбранный вами метод, насколько он отличается от описанных здесь. Маловероятно, что в данном случае вы нашли лучшие подходы.
Тем из вас, кто не пренебрегает моими комментариями, скажу следующее.
1. Сложные задачи иногда можно решать «по кусочкам». Их условия выполняются последовательно. Этот метод можно назвать поэтапным.
2. Если решение состоит из взаимосвязанных частей, поэтапный метод вам не поможет.
3. При поэтапном методе определяющим является выбор последовательности рассматриваемых стадий. Неверный выбор такой последовательности может завести вас в тупик, верный же не всегда очевиден.
4. Рассмотрение сложной задачи с различных точек зрения иногда способствует ее упрощению.
5. Решение сложной задачи может быть последовательно выведено из решения более простой задачи.
6. Даже если связь новой задачи с предыдущими не очевидна, можно попытаться модифицировать уже известные решения.
7. Модификация «методом вычитания» состоит в последовательном упрощении решения более сложной задачи.
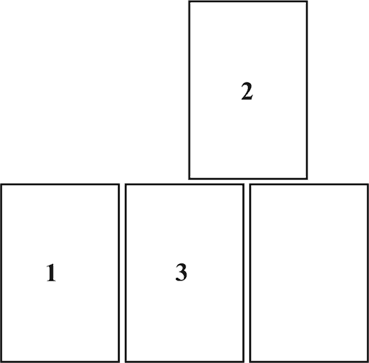
Рис. 18. Комбинация из четырех блоков с одним, двумя и тремя контактами.
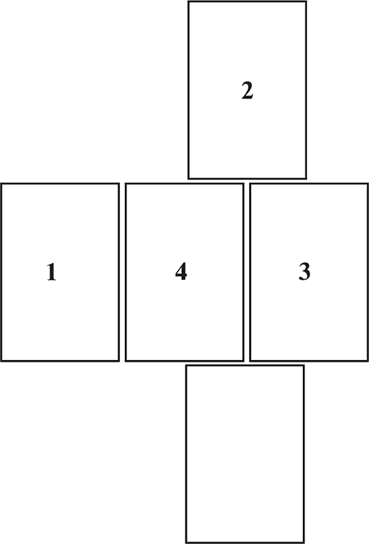
Рис. 19. Комбинация из пяти блоков с одним, двумя, тремя и четырьмя контактами.
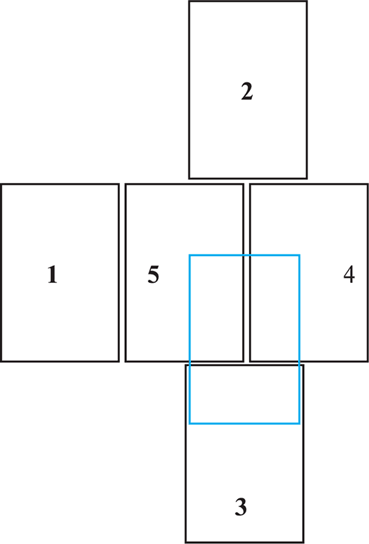
Рис. 20. Решение задачи 5, демонстрирующее число контактов от одного до пяти.
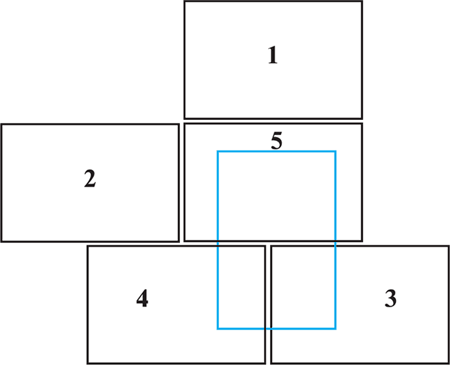
Рис. 21. Решение задачи 5, полученное из решения задачи 4.
Назад: Четвертый день
Дальше: Заключение

