АЛГЕБРА

Даже если вы, изучая в школе математику, все же совладали с делением больших чисел и десятичными дробями, то знакомство с алгеброй наверняка стало последней каплей, заставившей вас с диким воплем кинуться прочь, к пожарному выходу. И вас можно понять. Вычисление выражений, состоящих из чисел, кажется логичным, для того числа и придуманы. Но вычисление выражений с буквами? Какая-то бессмыслица… или нет?

Зачем все это?

Алгебра напоминает язык вроде русского или английского. Это быстрый способ описать и систематизировать задачу и, после того как вы усвоите основные правила, без лишней суеты найти ее решение. Представьте, что вы, будучи заграницей, хотите узнать у прохожих, где находится ближайшее вегетарианское кафе. Вы можете потратить не один час, пытаясь жестами изобразить морковку, а можете получить ответ за пару секунд, если знаете язык страны.

Что же касается букв, то ими просто обозначены числа, которые пока неизвестны. Чуть позже мы рассмотрим выражение для расчета стоимости чашки кофе, где искомая цена для краткости обозначена буквой c, чтобы не писать каждый раз «цена чашки кофе».

Мы даже не будем трогать буквы поначалу, а просто поглядим, как взаимодействуют между собой числа, чтобы прояснить основные правила.

Знаки «плюс», «минус» и «равно»

В середине этого простого выражения стоит знак равенства, поэтому оно называется уравнением:

7 – 2 = 4 + 1

Результат вычитания с левой стороны идентичен сумме чисел с правой стороны; оба равны 5. Суть алгебры в том, чтобы расположить определенным образом числа и буквы в уравнении и получить ответ.

Каждое число может быть либо положительным, либо отрицательным.

Перед отрицательными числами обязательно нужно ставить знак «–». Перед положительными числами тоже положено ставить знак «+», но делать мы это будем не всегда.

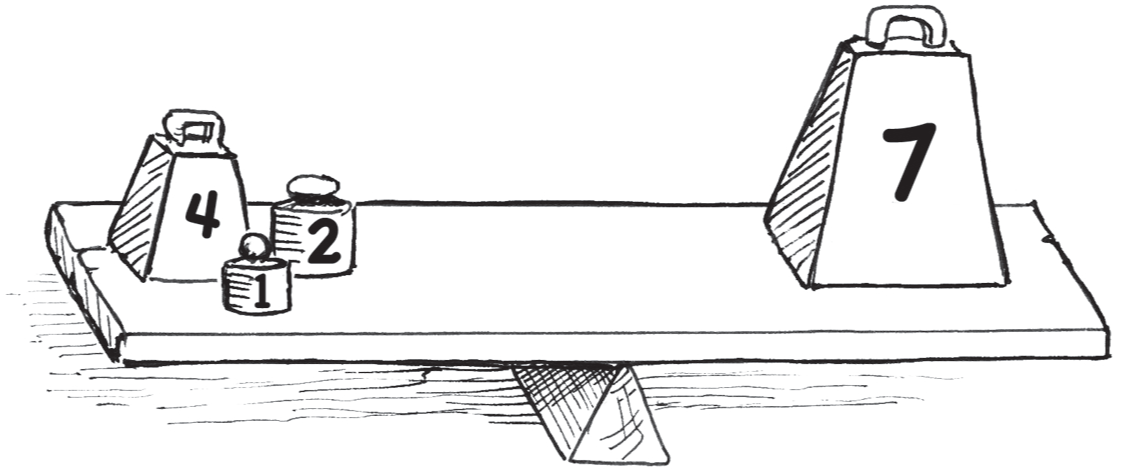
Уравнение можно представить себе в виде доски-качалки, где знак «равно» — точка опоры. Положительные числа — это грузы, прижимающие доску к земле, а отрицательные — воздушные шары, тянущие ее вверх.

7 – 2 = 4 + 1

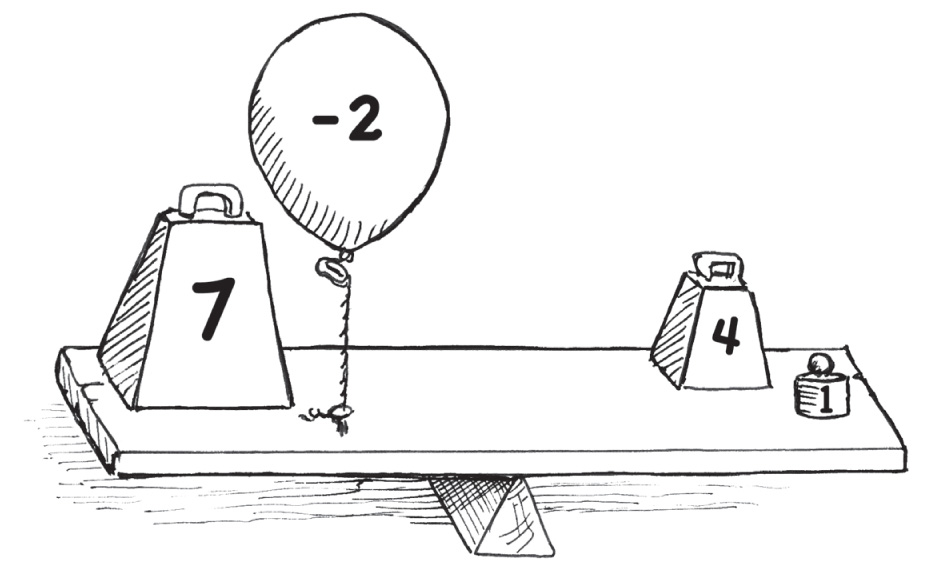
Если хотите переместить числа с места на место на одном конце доски, их знаки нужно перемещать вместе с ними. Поменяв местами числа с левой стороны, получим:

–2 + 7 = 4 + 1

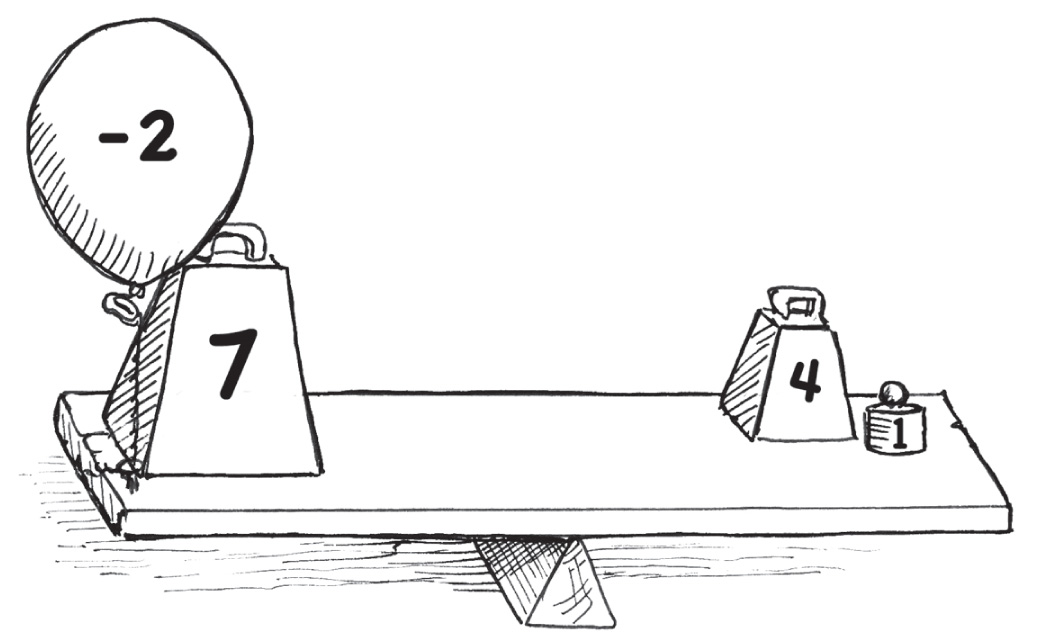
Знак «минус» должен оставаться перед числом 2, иначе уравнение станет неверным. Перед 7 появился знак «плюс» как напоминание, что оно положительное. Предположим, что нам нужно оставить в левой части уравнения только число +7. Существует всего одно золотое правило.

С уравнением можно делать все что угодно при условии, что с его обеими частями производятся одни и те же действия.

Чтобы в левой части осталось только +7, нужно избавиться от –2. Для этого добавим +2; однако, согласно правилу, это число нужно добавить к обеим частям уравнения.

–2 +7 +2 = 4 + 1 + 2

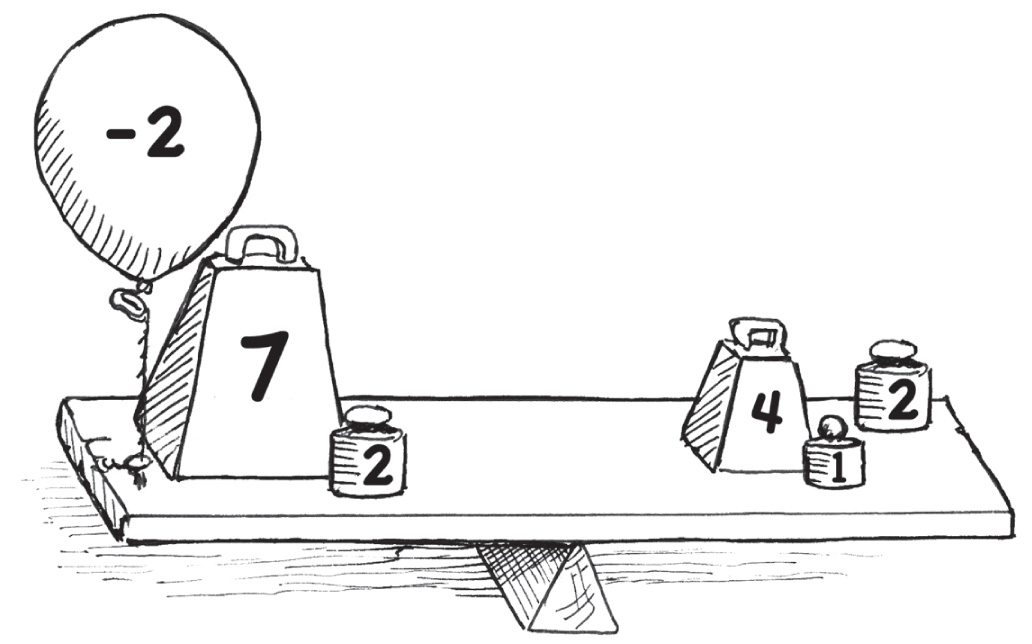
–2 и +2 с левой стороны уравнения взаимоуничтожатся, то есть дадут 0. С правой же стороны +2 останется, и мы получим:

7 = 4 + 1 + 2

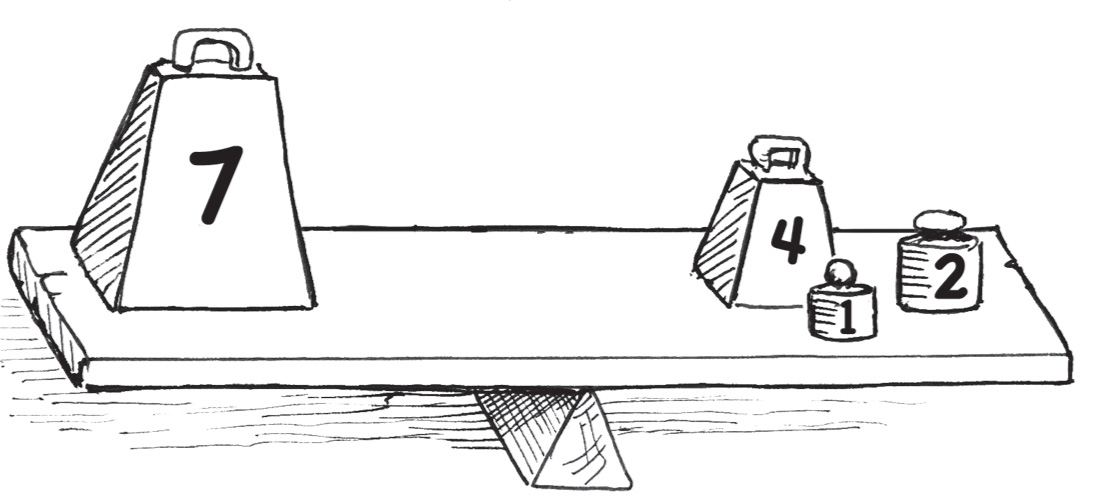
Выполнив подсчеты, вы убедитесь, что 7 и вправду равняется 4 + 1 + 2. При этом мы продемонстрировали маленькую хитрость.

При переносе числа через знак равенства меняется его знак! То есть «–» меняется на «+», а «+» на «–».

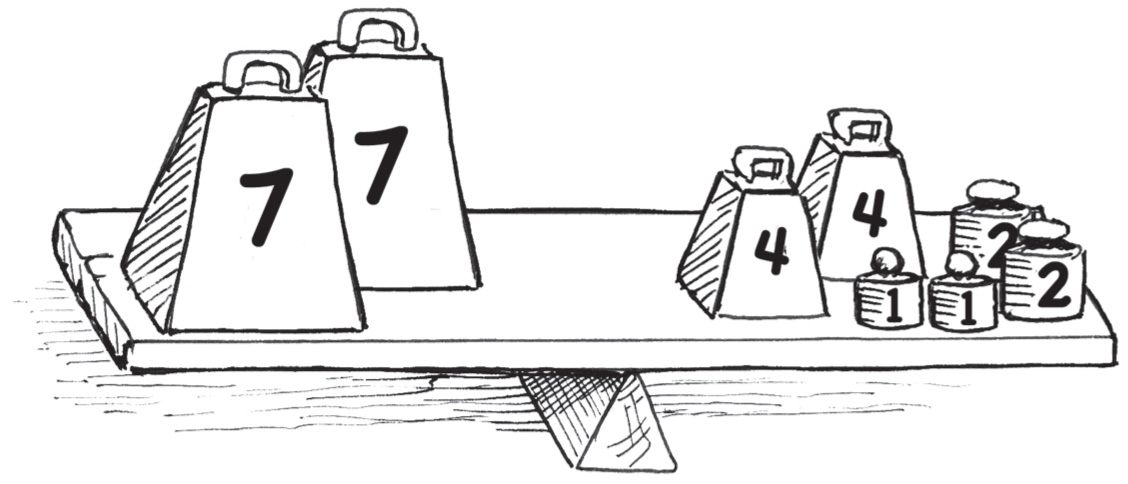
Вот еще одна вещь, которую можно показать на примере доски-качалки: вы можете менять две части уравнения мес­тами:

4 + 1 + 2 = 7

Скобки

Давайте пока остановимся на варианте 7 = 4 + 1 + 2. Предположим, что нам нужно знать, чему равно число 14. Для этого умножаем 7 на 2, но умножать также следует и другую часть уравнения. Поскольку с правой стороны стоят три числа, каждое из них необходимо умножить на 2 вот так:

2 × 7 = 2(4 + 1 + 2)

Как видите, мы заключили все числа с правой стороны в скобки. Можно было записать это иначе: 2 × 4 + 2 × 1 + 2 × 2, но со скобками получается короче и удобнее. Число 2 перед скобкой называется коэффициентом.

Если перед открывающей скобкой стоит число, то на него умножается все, что находится внутри скобок.

Добавляем буквы

Наверное, вам уже не терпится перейти к решению хитро­умных дифференциальных уравнений, однако начнем с ма­лого.

Прогуливаясь по улице, вы неожиданно встречаете Малькольма, который пребывает в легком шоке. Он только что водил маму в кофейню Barstucks, где они выпили по чашке кофе, и в результате из 10 фунтов, которые он брал с собой, осталось всего 1,20 фунта. Сколько же стоила каждая чашка? Вот что нам известно:

10 фунтов минус цена двух чашек кофе = 1,20 фунта

Мы сэкономим массу типографской краски, если обозначим цену одной чашки кофе буквой c. Из этого следует, что цена двух чашек кофе составит 2 × c, но для удобства мы просто напишем 2c.

Что ж, давайте составим уравнение и посмотрим, как быть дальше.

10 – 2c = 1,20

Нам нужно, чтобы слева от знака равенства была только буква c. Для начала перенесем 10 фунтов на другую сторону, поменяв знак на минус:

–2c = 1,20 – 10

Минус перед 2c выглядит не слишком привлекательно, по­этому избавимся от него, умножив обе части уравнения на (–1). В результате каждый знак «+» поменяется на «–», а каждый знак «–» на «+»:

2c = 10 – 1,20

Теперь подсчитаем 10 – 1,20 = 8,80, тогда

2с = 8,80

Поскольку нам нужна только одна с, разделим обе части на 2, и ответ готов:

с = 4,40 фунта

4,40 фунта за чашку кофе? Неудивительно, что Малькольм был в шоке!

Что можно и чего нельзя

В алгебре есть еще несколько на первый взгляд странных правил, поэтому, чтобы они стали понятнее, представим себе множество одинаковых коробков спичек. В каждом содержится m спичек, так что если мы отложим в сторону три коробка, общее количество спичек в них составит 3 × m, или просто 3m. Число 3 здесь — коэффициент при m.

Теперь, разобравшись с коробками, перейдем к правилам и выясним, как их применять к нашим спичкам.

1.-Коэффициент можно умножать на число

Если добавить еще одну стопку из трех коробков...

… то 2 стопки по 3m в сумме дадут 6m.

2.-Прибавлять число к коэффициенту нельзя

Если вы где-то нашли три спички...

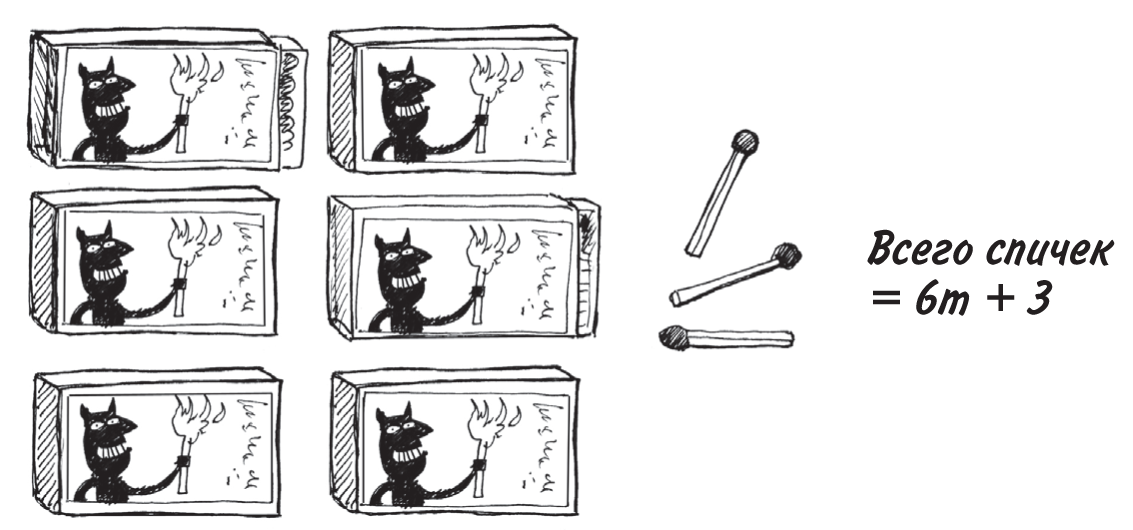
Видите, теперь у нас 6m + 3 спички. Нельзя прибавлять 3 к 6, чтобы получить 9m!

3.-Коэффициенты можно складывать, если при них одна и та же буква

Если взять еще два коробка...

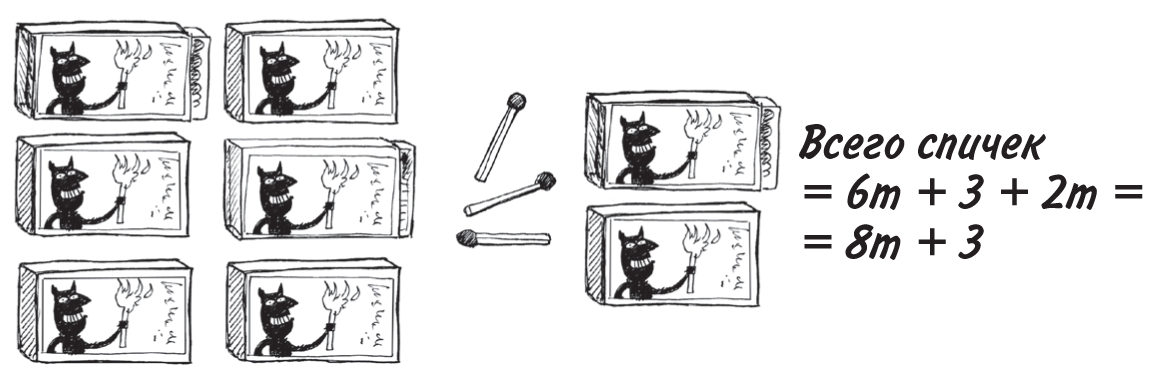
Как видите, складывать 6m и 2m, чтобы получить 8m, можно, но 3 прибавить к 8m по-прежнему нельзя.

Вот еще три правила. Не волнуйтесь, если сейчас они покажутся вам непонятными, чуть позже мы их применим, и все прояснится.

4.-Когда знак «минус» стоит перед скобками, избавляясь от них, надо поменять все знаки внутри скобок на противоположные

В выражении вроде 3 − (2x − 4) все, что внутри скобок, следует умножить на –1. Избавившись от скобок, вы получите 3 − 2x + 4. Вместо +2х стало –2х, а вместо –4 стало +4.

5.-Если умножить букву на саму себя, получается буква в квадрате

Таким образом, y × y превратится в y² (что такое числа в квадрате, мы обсуждали в разделе «Квадраты и квадратные корни»), а 4y × 3y — в 12y². Коэффициенты перемножаются, а у буквы появляется знак квадрата.

6.-При перемножении разных чисел и букв числа умножаются, а буквы пишутся вместе

Поэтому 2x × 4y = 8xy. Такие ситуации часто возникают при умножении содержимого скобок, например: 3p(7q − 2p) = 21pq − 6p².

Итак, давайте посмотрим, как это все может нам пригодиться.

Разгадка тайн математики с помощью алгебры

Алгебра бывает крайне полезна при решении задач и головоломок. Вот вам кое-что для начала.

Земельная афера

Бэтчап Билдингз решил приобрести надел земли у фермера Шарпа. Обе стороны сошлись на том, что это должен быть квад­ратный участок 20 м × 20 м, то есть площадью 400 квадратных метров, или м². Однако приехав осмотреть землю, Бэтчап увидел, что участок имеет прямоугольную, а не квадратную форму!

Честно ли поступает фермер?

Хотя мы не знаем, на сколько метров стороны участка длиннее или короче, нам известно, что это одна и та же величина, давайте назовем ее x. Нарисуем схему участка.

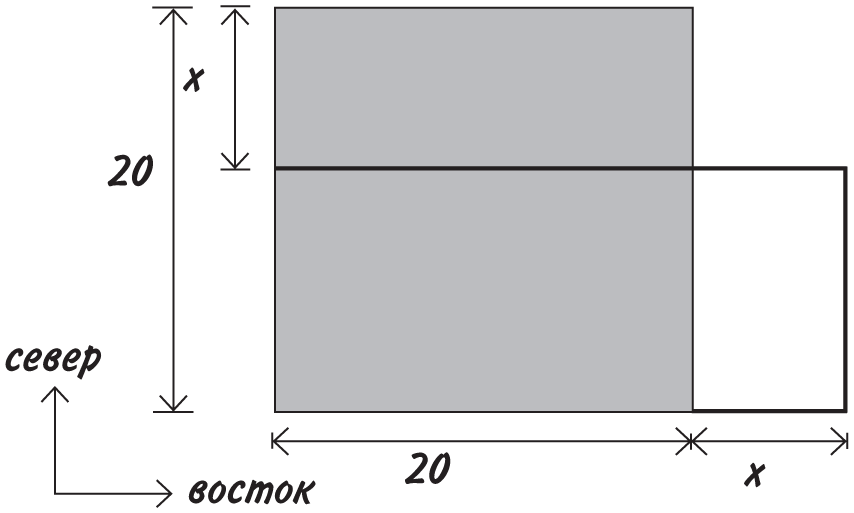
Серым цветом показано, как бы выглядел участок, будь это квадрат 20 м × 20 м. Размеры же прямоугольника: (20 – x) в северном направлении и (20 + x) в восточном. Чтобы узнать его площадь, перемножим эти значения и получим (20 − x) × (20 + x); знак умножения обычно не пишется: (20 − x)(20 + x).

При перемножении двух выражений в скобках все, что находится внутри одной пары скобок, умножается на все, что находится внутри другой пары.

Для этого раскрываем первые скобки и умножаем каждый элемент в них на вторые скобки. Получаем:

(20 − x)(20 + x) = 20(20 + x) − x(20 + x) =

= 400 + 20x − 20x − x² =

= 400 − x²

Как видите, раскрывая −x(20 + x), мы первым делом умножаем −x × 20 = −20x. Обратите внимание, знак «минус» никуда не исчезает. И наконец, умножаем −x × x, что дает −x². В следующей строке +20x и −20x взаимоуничтожаются, и мы получаем любопытный результат: 400 − x². О чем это говорит?

Будь участок квадратным, Бэтчап приобрел бы обещанные 400 квадратных метров земли. Однако после изменения формы участка его площадь уменьшилась на x². И чем больше значение x, тем больше земли теряет Бэтчап. (Помните, буква x обозначает, насколько стороны длиннее/короче одна другой.)

Если участок на 5 метров длиннее в одном направлении и на 5 метров короче в другом, тогда x = 5. Мы можем вычислить площадь такого участка двумя способами. Во-первых, взяв полученный ранее ответ 400 − x² и подставив вместо x число 5. Площадь составит 400 − 5², то есть 400 − 25 = 375. Во-вторых, просто перемножив длины сторон прямоугольника. В северном направлении это 20 − 5 = 15, а в восточном — 20 + 5 = 25. Тогда площадь равна 15 × 25 = 375. Оба ответа совпадают, стало быть, алгебра работает как надо!

Разность квадратов

Допустим, у вас есть квадратный блок почтовых марок размером 6 × 6. Кто-то оторвал от него несколько марок, оставив вам квадрат 4 × 4. Сколько марок забрали?

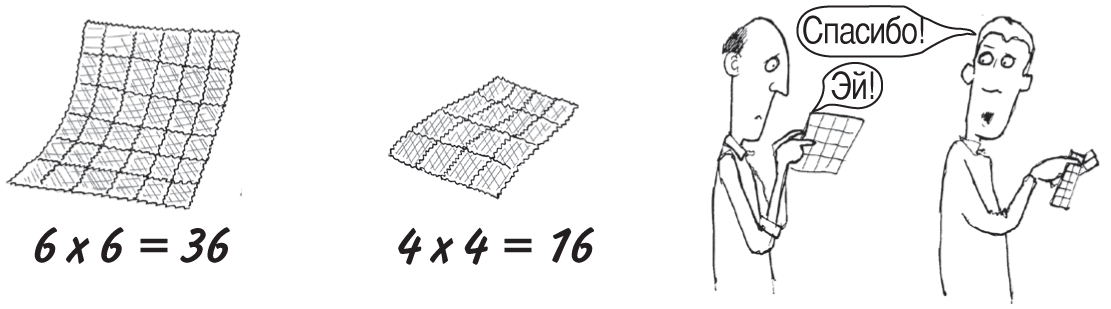
Нам нужно вычислить 6² − 4². Вычитание квадрата одного числа из квадрата другого называется разностью квадратов. В данном случае все просто, поскольку числа небольшие. Получаем 36 − 16 = 20. Однако есть более быстрый способ подсчета, который подходит для квадратов любых чисел.

Разность квадратов двух чисел равняется сумме этих чисел, умноженной на их разность.

Звучит довольно странно, однако вот что это означает: чтобы вычислить 6² − 4², сначала нужно узнать сумму двух чисел: 6 + 4 = 10. Кроме того, понадобится их разность: 6 − 4 = 2. Теперь умножаем сумму на разность: 10 × 2 = 20. Такой же ответ мы получили раньше.

Вместо того чтобы рассуждать об этом на словах, проще записать правило разности квадратов в виде алгебраического уравнения. Обозначим буквой a первое число и буквой b второе, тогда наше правило будет иметь следующий вид:

a² – b² = (a + b)(a – b)

Мы уже наблюдали, как это работает для a = 6 и b = 4, однако данное уравнение подходит для любых a и b. Если вы думаете, что разность квадратов вам никогда не пригодится в жизни, представьте, что a = 20 и b = x, и посмотрите на уравнения из задачки о земельной афере. Там у нас (20 − x)(20 + x) = 400 − x², тот же самый результат!

Объяснение загадки с тремя числами

Помните подраздел «Фокус с тремя числами», размещенный в начале книги? Там я объяснял, что какими бы ни были три последовательно идущих числа, если умножить большее из них на меньшее, результат всегда будет на единицу меньше второго числа, возведенного в квадрат. Например, возьмем 12, 13 и 14. Результат умножения 12 × 14 = 168, что на единицу меньше, чем 13² = 169.

Опять воспользуемся уравнением для разности квадратов, подставив вместо b единицу. Вот что получится:

a² – 1² = (a + 1)(a – 1)

Вспоминаем, что 1² = 1 × 1 = 1, поэтому выходит

a² – 1 = (a + 1)(a – 1)

Теперь предположим, что a — второе из трех последовательно идущих чисел. Тогда (a + 1) будет наибольшим числом, а (a – 1) — наименьшим. Уравнение говорит нам, что если взять квадрат второго числа и вычесть из него единицу, то результат будет равен наибольшему числу, умноженному на наименьшее.

В случае с числами 12, 13 и 14 a = 13, но, разумеется, вместо 13 можно выбрать любое другое значение. Вот почему этот фокус применим к любым трем последовательно идущим числам.

Алгебра отлично подходит для разоблачения фокусов из серии «загадать любое число».

Как разрушить Вселенную

Помните, выше я предупреждал вас о такой вероятности? Если вы дочитали до этого места, значит, усердно трудились и многое узнали, поэтому будет совершенно справедливо вознаградить вас за старания неограниченными космическими суперспособностями...

Начнем с двух чисел, a и b, которые волей случая оказались равны:

a = b

Будем обращаться с обеими частями этого уравнения совершенно одинаковым образом. Смотрите внимательно...

Умножаем обе части на a: a² = ab

Вычитаем из обеих частей b²: a² — b² = ab — b²

С левой стороны уравнения получается разность квадратов, поэтому, как мы знаем, a² − b² = (a + b)(a – b). С правой стороны выходит ab − b², где оба элемента делятся на b, стало быть, это выражение можно записать как b(a − b). Все эти действия допустимы и абсолютно корректны.

Таким образом, получаем (a + b)(a — b) = b(a — b)

Теперь разделим обе части на (a – b) и получим (a + b) = b

Перед скобками множителя нет, а значит, их можно просто убрать

a + b = b

Переносим +b в другую часть уравнения, меняя знак:

a = b – b

И вот итог: a = 0

Теперь вспоминаем, что a и b могут быть любыми числами, следовательно, мы только что доказали, что любое число равно нулю. То есть получается, что любые измерения времени, пространства или веса несущественны: прощай, Вселенная!

Наша ошибка состояла в том, что мы разделили обе части уравнения на (a − b). Но в случае, когда a = b, (a − b) = 0. Единственное, чего нельзя делать одновременно с обеими частями уравнения, — это делить на ноль! Если, конечно, вы не собираетесь потратить денек-другой на попытки разрушить Вселенную...

Системы уравнений

Если два неизвестных числа входят в два различных уравнения, их, как правило, можно найти.

Вот классическая задачка. Пара ботинок и щетка для обуви стоят 51 фунт, причем ботинки на 50 фунтов дороже щетки. Какова цена щетки?

Попробуйте спросить об этом Малькольма. Скорее всего, он ответит, что щетка стоит 1 фунт, а ботинки 50 фунтов, но тогда получается, что ботинки лишь на 49 фунтов дороже щетки... Выходит, Малькольм ошибается?!

Поразмыслив, вы можете угадать ответ, но я хочу рассказать, как получить его с помощью алгебры. Обозначим цену ботинок буквой s, а цену щетки c. К счастью, у нас достаточно сведений, чтобы составить два уравнения:

Уравнение 1. Ботинки и щетка стоят 51 фунт: s + c = 51

Уравнение 2. Ботинки стоят на 50 фунтов дороже щетки: s = 50 + c

Простейший способ решения системы уравнений называется подстановкой. Исходя из уравнения 2, s = 50 + c, поэтому перепишем уравнение 1, подставив туда (50 + c) вместо s.

Получаем:

50 + c + c = 51

Меняя знак, переносим 50 в другую часть уравнения и складываем две буквы c:

2c = 51 — 50

Тут все просто…

2c = 1

И наконец, делим обе части уравнения на 2, чтобы узнать цену щетки:

c = 0,5 = 50 пенсов

Согласно уравнению 2, s = 50 + c, так что получаем:

s = 50,5 фунта

Выходит, ботинки стоят 50,5 фунта, а щетка 0,5 фунта. Ответ неожиданный, но верный!

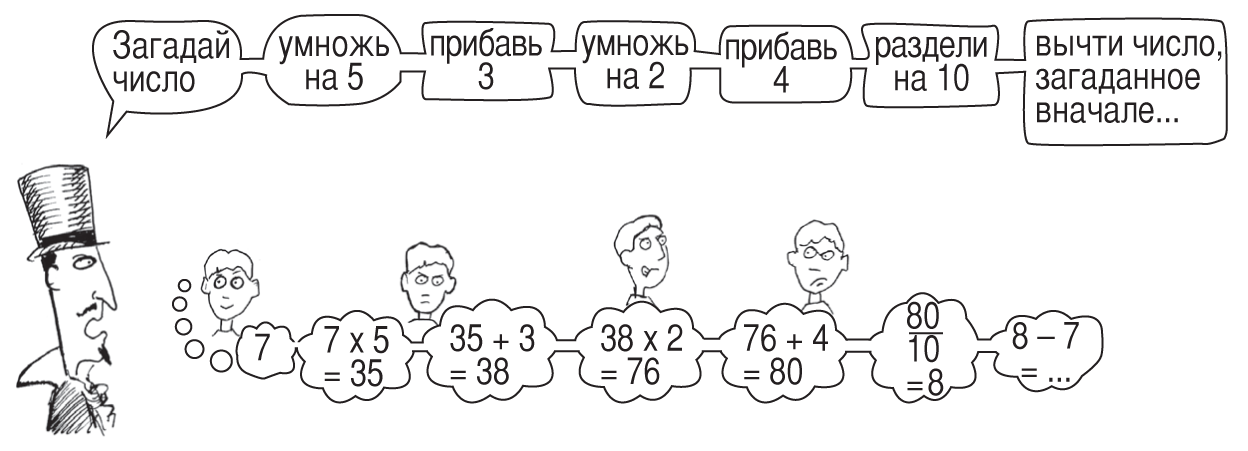
Этот трюк можно проделать с любым числом, даже дробью. Давайте с помощью алгебры разберемся, что здесь к чему. Число нам неизвестно, поэтому просто назовем его n и посмотрим, что с ним происходит по мере выполнения разных действий.

Действие	Что происходит	Промежуточный результат
Загадай число	Назовем его n	n
Умножь на 5	Теперь у нас есть 5n	5n
Прибавь 3	5n + 3. Пока все нормально	5n + 3
Умножь на 2	Умножаем на 2 все имеющееся на текущий момент; для верности ставим скобки	2(5n + 3) = 10n + 6
Прибавь 4	Тут все просто	10n + 6 + 4 = 10n + 10
Раздели на 10	Нужно все разделить на 10, снова используем скобки	(10n + 10) ÷ 10 = n + 1
Вычти загаданное число	Просто вычитаем n	n + 1 – n = 1
Получается 1	n полностью исчезает из уравнения, остается единица!

Хватит алгебры

Заглянув в школьные учебники, вы увидите множество всяких x, y и задач, которые сводятся к перестановкам чего-либо с привлечением толики здравого смысла. Есть масса толстенных книг по алгебре, поэтому понятно, что я не могу рассказать здесь обо всем, но вот еще одна задачка, которую алгебра помогает решить весьма точно и элегантно.

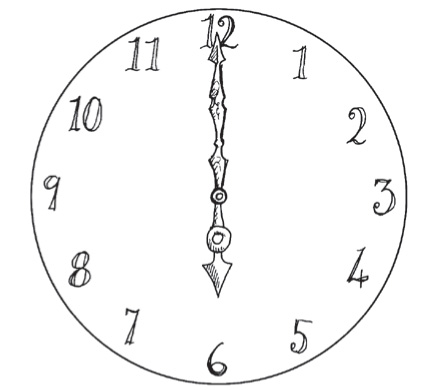
На старинных часах ровно 6 часов вечера. Сколько будет времени, когда минутная стрелка догонит часовую?

Разумеется, сложность в том, что часовая стрелка постоянно медленно движется. Как же это учесть?

Допустим, m — это количество минут, прошедших после 6 часов до того момента, когда минутная и часовая стрелки совпадут.

Минутной стрелке понадобится 30 минут, чтобы добраться до цифры 6, плюс пройти дистанцию, которую преодолеет часовая стрелка за m минут. Давайте это запишем:

Нам нужно выяснить, как далеко продвинется часовая стрелка за m минут.

Минутная стрелка делает один полный оборот в час. Часо­вой стрелке нужно 12 часов, чтобы сделать полный оборот, то есть ее скорость — 1/12 от скорости минутной.

Составим уравнение:

m = 30 + m/12

Число 12 в качестве знаменателя выглядит отвратительно, однако не волнуйтесь — мы умножим на 12 обе части уравнения:

12m = 360 + m

Перенесем + m в другую часть уравнения, поменяв знак:

12m — m = 360

Вычтем 1m из 12m:

11m = 360

Разделим обе части на 11:

m = 32,727

Выходит, стрелки совпадут через 32,727 минуты после 6 часов вечера. Однако 0,727 минуты в ответе смотрятся некрасиво. Поскольку в минуте 60 секунд, в секундах это будет 0,727 × 60, то есть около 44 секунд. Теперь у нас есть понятный ответ: стрелки совпадут в 6:32:44 вечера.

Отправить