8. Связи

Книга: Мозгоускорители. Как научиться эффективно мыслить, используя приемы из разных наук

Статистика может быть полезна, а иногда даже необходима, чтобы дать чему-либо точную характеристику. Кроме того, статистика позволяет определить, существует ли связь между одним явлением и другим. Как несложно догадаться, с уверенностью говорить о наличии или отсутствии связей между явлениями может быть еще труднее, чем точно охарактеризовать какое-либо явление, предмет или человека.

Вам нужно правильно охарактеризовать явление 1, а также явление 2. Затем вам нужно подсчитать, насколько часто явление первого типа возникает вместе с явлением второго типа, как часто явление первого типа не возникает вместе с явлением второго типа и т.д. Если переменные величины непрерывны, задача усложняется еще больше. Нужно рассчитать, связаны ли более высокие показатели явлений первого типа с более высокими показателями явлений второго типа. Даже такое абстрактное рассуждение ясно дает понять, что у нас возникнут большие проблемы при попытке оценить степень связи между переменными величинами. И в самом деле, наши трудности с поиском ковариаций (или корреляций) очень серьезны. А последствия наших ложных оценок могут быть весьма и весьма неблагоприятными.

Корреляция

Посмотрите на таблицу 3 внизу. Связан ли симптом X с болезнью А? Другими словами, можно ли по симптому X диагностировать болезнь А?

Таблица 3. Связь между болезнью А и симптомом X

В таблице 3 говорится о том, что у 20 человек, страдающих болезнью А, присутствует симптом X, а у 80 человек, страдающих болезнью А, он отсутствует; при этом у десяти человек, не страдающих болезнью А, также присутствует этот симптом, а у 40 человек, не страдающих этой болезнью, отсутствует. На первый взгляд может показаться, что это простейшая задача на поиск ковариации, которую только можно себе представить. Вариантов всего два (или/или). Вам не нужно собирать информацию, или кодировать исходные данные и присваивать им численные значения, или вспоминать всю информацию об этих данных. У вас нет никаких предубеждений, которые могут повлиять на ваш выбор в пользу одного ответа, а не другого; и информация представлена для вас уже в виде сводки. Как же люди справляются с этой базовой задачей на поиск ковариации?

На самом деле очень плохо.

Самая распространенная ошибка в решении этой задачи — полагаться исключительно на графу «да/присутствует». «Да, этот симптом связан с этой болезнью. У некоторых людей с симптомом X обнаружена эта болезнь». Тенденция к выражению такого рода мнения является примером необъективности подтверждения — склонности искать доказательства, которые подтвердят уже имеющуюся гипотезу, не учитывая при этом тех доказательств, которые могут эту гипотезу опровергнуть.

Другие, взглянув на таблицу, обращают внимание на две графы. Кое-кто делает вывод, что симптом связан с этой болезнью, «потому что людей, имеющих этот симптом и страдающих этой болезнью, больше, чем людей, имеющих этот симптом и не болеющих этой болезнью». Другие делают вывод, что симптом не связан с болезнью, «потому что среди страдающих этой болезнью людей больше тех, кто не имеет этого симптома, чем тех, кто его имеет».

Не имея представления о статистике как науке, мало кто понимает, что нужно принимать во внимание все четыре графы таблицы, чтобы суметь ответить на простой вопрос о связи между этими двумя явлениями.

Нужно составить пропорцию для сравнения количества людей, у которых диагностировали данное заболевание в сочетании с данным симптомом, и количества людей, у которых обнаружили данную болезнь, но не этот конкретный симптом. Затем вы составляете пропорцию для сравнения количества людей, у которых нет данного заболевания, но есть этот симптом, и количества людей, у которых нет заболевания и нет симптома. Так как в результате получаются две одинаковые пропорции, мы понимаем, что этот симптом ничуть не больше связан с этой болезнью, чем с ее отсутствием.

Вас, наверное, встревожит тот факт, что большинство людей, включая врачей и медсестер, которые ежедневно занимаются лечением болезней, как правило, затрудняются дать правильный ответ при изучении таких данных, как приведенные в таблице 3. К примеру, можно показать им таблицу, в которой отмечено, сколько больных некой болезнью выздоровели в результате определенного вида лечения, сколько не выздоровели, а также сколько больных выздоровели без этого лечения и не выздоровели без этого лечения. Врачи иногда могут предположить, что определенное лечение помогает больным, потому что из получивших его большее количество людей выздоровело, чем не выздоровело. Но, не зная соотношения этого количества людей с количеством выздоровевших без этого лечения и количеством людей, не выздоровевших без этого лечения, невозможно сделать верные выводы. В связи с этим такие таблицы иногда называют таблицы 2x2, или четырехпольные таблицы.

Существует статистический критерий, называемый хи-квадрат, который рассматривает вероятность того, что две пропорции достаточно отличаются друг от друга, чтобы можно было с уверенностью утверждать, что перед нами подлинная взаимосвязь явлений. Мы называем взаимосвязь подлинной, если разница между двумя пропорциями статистически значима.

Типичный критерий, на основе которого можно утверждать, значима связь или нет, формулируется так: показывает ли тест (хи-квадрат или любой другой статистический тест), что данная степень связи может оказаться случайной лишь в пяти случаях из ста. Если так, мы говорим, что уровень статистической значимости равен 0,05. Тест оценки значимости можно применять не только к дихотомическим данным (или/или), но и к непрерывным.

Когда мы имеем дело с непрерывными случайными величинами и хотим знать, насколько тесно они связаны одна с другой, мы применяем статистический метод корреляции. Возьмем две переменные величины, которые очевидно коррелируют между собой, — рост и вес. Конечно, связь между ними не абсолютная, потому что, как мы знаем, есть много примеров невысоких людей с относительно большим весом и, наоборот, высоких людей с относительно небольшим весом.

Статистические методы могут рассказать нам о том, насколько тесна связь между двумя величинами. Один из часто используемых методов исследования степени связи между непрерывными величинами называется методом корреляции смешанных моментов Пирсона. Корреляция, равная 0, означает, что между двумя величинами нет никакой связи. Корреляция, равная +1, означает, что между двумя величинами существует полная положительная связь, то есть если значение первой величины увеличивается, то значение второй величины увеличивается в соответствующей степени. Корреляция, равная -1, означает полную отрицательную связь.

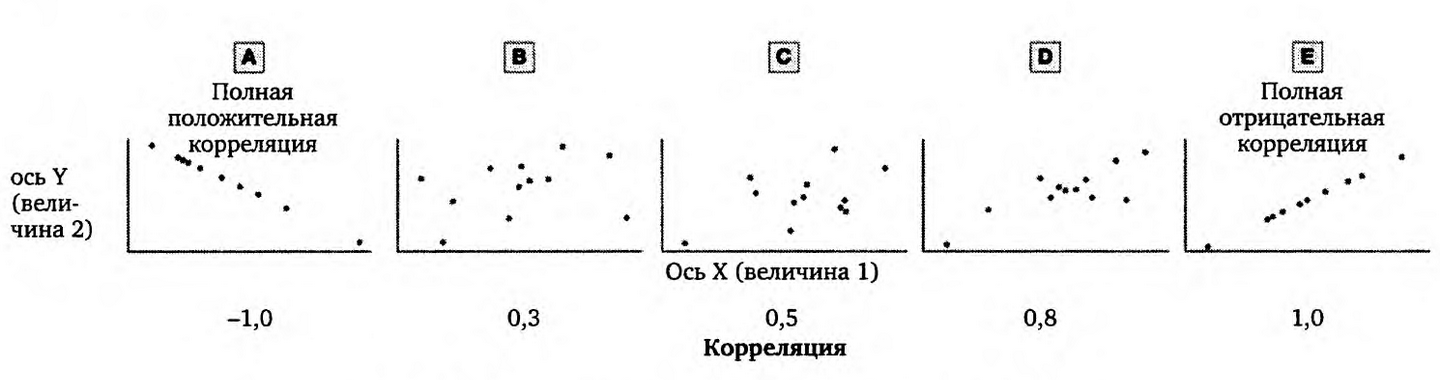
Рис. 3. Диаграмма разброса и корреляции

На рисунке 3 с помощью так называемых диаграмм разброса показано, насколько велика корреляция такого масштаба. Отдельные графики называются диаграммами разброса, потому что они показывают степени разброса относительно прямой линии — полной функциональной связи.

Корреляцию, равную 0,3, трудно распознать визуально, но на практике она может быть очень важна. Корреляция уровня 0,3 соответствует, например, прогнозируемости уровня дохода в зависимости от IQ или успеваемости в аспирантуре в зависимости от оценок в колледже. В такой же степени можно спрогнозировать вероятность развития сердечно-сосудистых заболеваний в зависимости от веса человека.

Корреляция 0,3 это вовсе не пустяк — это значит, что если кто-то находится в 84-м процентиле (одно СКО выше среднего значения) переменной величины А, то этот человек скорее всего будет в 63-м процентиле по величине Б (0,3 СКО выше среднего значения). А это уже более высокая прогнозируемость для величины Б, чем та, что была у вас, когда вы ничего не знали о величине А. В этом случае вы должны догадаться, что 50-й процентиль для каждого — среднее значение распределения величины Б. Иногда такой факт может решить судьбу вашего бизнеса — будет он процветать или обанкротится.

Корреляция 0,5 соответствует степени связи между уровнем 1(2 и качеством исполнения служебных обязанностей на средней должности. (Корреляция в данном случае будет выше, когда работа сложная и ответственная, и ниже, когда работа более легкая.)

Корреляция 0,7 соответствует степени связи между ростом и весом — она существенна, но все же это не полная взаимосвязь. Корреляция 0,8 соответствует степени связи между баллами за тестирование знаний по математике за один год и баллами за этот же тест на следующий год — это довольно высокая корреляция, но все же разница между двумя оценками в среднем может быть велика.

Корреляция не означает наличие причинно-следственной связи

Расчет коэффициента корреляции — только один из шагов в определении причинно-следственных связей. Если между величиной А и величиной Б нет корреляции, тогда между ними (вероятно) нет и причинно-следственной связи. (Исключением может быть такой случай, когда существует третья величина В, которая маскирует корреляцию между А и Б, когда между ними на самом деле есть причинно-следственная связь.) Если между А и Б есть корреляция, это еще не говорит о том, что изменение величины А является причиной изменения величины Б. Возможно, А влияет на Б или Б влияет на А, а также ассоциация может возникнуть вследствие того, что А и Б связаны с некой третьей величиной В, но между А и Б нет никакой причинно-следственно связи.

Практически любой человек с высшим образованием признает, что теоретически эти утверждения верны. Но зачастую конкретная корреляция настолько согласуется с весьма правдоподобными объяснениями некой взаимообусловленности, что мы автоматически принимаем ее как доказательство наличия причинно-следственной связи. Нам так хорошо удается строить гипотезы о причинах и следствиях, что это происходит практически само собой. Выводы о причинах и следствиях, которые возникают у нас в голове, часто бывают настолько соблазнительны, что нам трудно от них отказаться. Если я скажу вам, что у людей, которые едят много шоколада, чаще бывают прыщи, трудно не сделать вывод, что шоколад вызывает появление прыщей. (Как известно, это не так.) Если я скажу вам, что пары, которые тщательно готовятся к свадьбе, потом дольше живут в браке, у вас возникнет естественный вопрос: каким же образом тщательно продуманная свадебная церемония продлевает брак? Не так давно в статье в одной очень известной газете автор утверждал, что такая корреляция существует, и пускался в размышления, почему совместная работа по планированию свадьбы производит такой эффект. Если поразмыслить над этой корреляцией, вы поймете, что тщательное планирование свадьбы не является случайным событием; скорее, можно сказать, что это событие с большей вероятностью произойдет у тех, у кого больше друзей, больше свободного времени друг для друга, больше денег и много чего еще. Любой из этих аспектов, а лучше сказать, все они и влияют на продолжительность брака. Не стоит выдергивать из запутанной паутины событий один-единственный факт и начинать раздумывать о том, как же так получилось. Это ни к чему не приведет.

Взгляните на причинно-следственные связи, изложенные в подборке 1. Все они реальны. Некоторые из них выглядят весьма правдоподобно, другие наоборот — весьма неправдоподобно. Независимо от того, считаете вы причинно-следственную связь правдоподобной или нет, подумайте, можете ли вы дать объяснения следующих типов: 1) А приводит к Б; 2) Б приводит к А; 3) что-либо, связанное и с А, и с Б, оказывает влияние, а между А и Б нет связи. Затем взгляните на возможные ответы в подборке 2.

Подборка 1. Размышляем о корреляциях: какими могут быть причинно-следственные связи?

1. В статье, опубликованной в журнале Time, утверждается, что попытки родителей контролировать, сколько едят их дети, приводят к тому, что дети набирают избыточный вес. Если родители перестанут контролировать количество еды, похудеют ли эти дети?

2. В тех странах, где выше средний уровень IQ, выше и среднее благосостояние граждан, измеряемое в ВВП на душу населения. Делает ли наличие умных людей страну богаче?

3. Уровень смертности среди людей, посещающих церковь, ниже, чем среди тех, кто церковь не посещает. Означает ли это, что вера в Бога делает жизни людей длиннее?

4. Владельцы домашних животных реже страдают от депрессии. Если подарить страдающему от депрессии человеку кота, станет ли он счастливее?

5. В странах, в которых пропагандируется воздержание от сексуальной жизни, совершается больше убийств. Вызывает ли агрессию пропаганда воздержания от сексуальной жизни? Если изменить данную область образования и больше рассказывать людям о сексуальной жизни, снизится ли в этих странах процент убийств?

6. У умных мужчин сперма лучше — ее больше и она более активна. Означает ли это, что учеба в колледже, благодаря которой можно стать умнее, также улучшает качество спермы?

7. Те, кто курит марихуану, с большей вероятностью будут употреблять также и кокаин, чем те, кто не курит марихуану. Значит ли это, что курение марихуаны приводит к употреблению кокаина?

8. В 1950-е гг. была установлена практически полная корреляция между употреблением мороженого и заболеванием полиомиелитом, представлявшем тогда серьезную угрозу. Разумно ли было бы запретить продавать мороженое в те годы?

Подборка 2. Возможные ответы на вопросы о корреляциях из подборки 1

1. Возможно, родители начинают контролировать количество еды, съедаемой ребенком, если у ребенка появляется избыточный вес. В таком случае направление причинно-следственной связи прямо противоположно гипотезе журнала Time. Вы не вызываете у ребенка ожирение, контролируя размер его порций, — вы начинаете контролировать ребенка, если у него появится избыточный вес. Бывает также, что в не очень счастливых семьях, где царит атмосфера стресса, родители чрезмерно контролируют детей, а дети страдают от ожирения, но и в этом случае не наблюдается причинно-следственной связи между попытками контроля питания и весом ребенка.

2. Возможно, в более благополучных странах лучше развита система образования, а значит, у людей есть возможность достигать высокого уровня IQ. В этом случае благосостояние влияет на уровень интеллекта, а не наоборот. Также возможно, что какой-нибудь третий фактор, например физическое здоровье, влияет как на благосостояние общества, так и на уровень интеллекта граждан. (Между прочим, все три эти причинно-следственные связи существуют на самом деле.)

3. Возможно, более здоровые люди в принципе чаще участвуют в различных событиях социальной жизни, включая посещение церкви. Если так, направление причинно-следственной связи здесь прямо противоположно тому, что подразумевается в вопросе: не посещение церкви делает людей здоровее, а люди ходят в церковь, потому что они здоровы. Или, может быть, интерес к социальной жизни, такой как посещение церкви, побуждает людей и быть более активными, и оставаться более здоровыми.

4. Возможно, люди, страдающие от депрессии, менее склонны предпринимать что-либо для своего развлечения, например заводить домашнее животное. А если так, значит, вновь перепутаны причина и следствие: не покупка кота снижает вероятность депрессии, а депрессия снижает вероятность покупки кота. (На самом деле если человеку, страдающему от депрессии, подарить домашнего питомца, это может улучшить его настроение, так что животные действительно положительно влияют на наше психологическое состояние; однако для доказательства этого одной только корреляции между присутствием кота и отсутствием депрессии недостаточно.)

5. Возможно, в бедных государствах чаще совершаются убийства, а также пропагандируется воспитание в духе безусловного воздержания от секса. (На самом деле то и другое правда.) Поэтому между сексуальным просвещением и убийствами может вовсе не быть причинно-следственной связи. Скорее с ними могут быть связаны бедность, низкий образовательный уровень или какие-то следствия этих социальных бед.

6. Возможно, крепкое здоровье помогает людям быть умнее и улучшает качество спермы. А возможно, дело в каком-то другом факторе, связанном и с интеллектом, и с качеством спермы, например в отказе от алкоголя или наркотиков. Таким образом, между интеллектом и качеством спермы может не быть никакой причинно-следственной связи.

7. Возможно, люди, которые употребляют наркотики любого вида, более склонны к поиску новых ощущений, а потому они пробуют что-то, возбуждающее эмоции, даже если это противозаконно. Курение марихуаны не приводит к употреблению кокаина, так же как и употребление кокаина не приводит к курению марихуаны. Скорее, на то и другое влияет третий фактор — жажда новых ощущений.

8. В 1950-е гг. была установлена высокая корреляция между потреблением мороженого и заболеванием полиомиелитом, потому что полиомиелитом было легко заразиться в бассейнах и водоемах. А дети едят мороженое и купаются в одно и то же время года — летом.

Иллюзорная корреляция

Невозможно описать, как это важно — собирать данные систематически, а затем делать расчеты, чтобы определить, насколько сильна ассоциация между двумя переменными величинами. Это необходимо, потому что, просто живя и наблюдая за явлениями в мире, можно постоянно получать безнадежно неверное представление о взаимосвязи между событиями. Риск иллюзорной корреляции абсолютно реален.

Если вы считаете, что положительная корреляция между двумя величинами кажется правдоподобной (чем больше А, тем больше Б), ваши наблюдения за причинами и следствиями, скорее всего, еще больше убедят вас, что вы правы. Но часто так бывает не только когда положительная корреляция между величинами отсутствует, но и тогда, когда между ними имеется отрицательная корреляция. Если вы видите и вспоминаете больше тех случаев, которые поддерживают вашу гипотезу, чем тех, что опровергают ее, это еще одно проявление необъективности подтверждения.

И наоборот, если связь кажется вам неправдоподобной, вы вряд ли обнаружите ее, даже если она очень сильна. Психологи сажали голубей в помещение с автоматической кормушкой. На полу был установлен диск, который время от времени светился. Корм появлялся тогда, когда светился диск, и при условии, что голубь не клевал сам диск. Если голубь начинал клевать диск, корм не появлялся. Птица едва не умирала от голода, прежде чем понимала, что, если не клевать диск, появится корм. Голуби считали неправдоподобным, что если не клевать что-то, то от этого появится корм.

Так же, как этим голубям, людям бывает трудно перешагнуть через свои изначальные предположения. Экспериментаторы демонстрировали клиническим психологам страницы теста Роршаха якобы с ответами пациентов о возникших у них ассоциациях. Там же были написаны симптомы психологических нарушений, якобы выявленные у этих несуществующих пациентов. Например, на одной картинке было обозначено, что пациент а) увидел на рисунке гениталии и б) у него имеются сексуальные расстройства. После этого клинические психологи довольно часто утверждали, что пациенты, увидевшие на рисунке гениталии, скорее всего имеют проблемы сексуального характера, даже если все имеющиеся данные говорили, что эти пациенты менее склонны к сексуальным расстройствам. Однако идея о том, что проблемы сексуального характера могут сочетаться с повышенным вниманием к гениталиям, выглядит очень правдоподобной, и подтверждающие это примеры более заметны.

Когда психологам говорили, что они ошибаются и результаты теста Роршаха выявили отрицательную корреляцию (у пациентов, которые видят гениталии, менее вероятны сексуальные отклонения), это вызывало у испытуемых усмешку. Они утверждали, что в их клинической практике гениталии на картинках теста Роршаха чаще видят люди с сексуальными проблемами. В действительности это не так. Анализ имеющихся данных по тесту Роршаха такой связи не показывает.

На самом деле ассоциации могут быть практически любыми, и они ничего не скажут вам о человеке. На исследования с помощью теста Роршаха были потрачены сотни тысяч часов и миллионы долларов, прежде чем кто-то задался вопросом, а есть ли связь между ответами и симптомами. Но еще несколько десятков лет после того, как отсутствие связи было установлено, иллюзия корреляции продолжала поддерживать популярность этого теста и заставляла вновь и вновь тратить время и средства.

Я не собираюсь придираться к психологам и психиатрам с этими примерами. Выпускники университетов допускают те же самые ошибки, что и врачи, ставя эксперименты над иллюзорной корреляцией с использованием теста Роршаха и отмечая, что, если пациент видит на рисунках гениталии, это говорит о его сексуальных проблемах, если чьи-то глаза — это свидетельство паранойи, а если оружие — то враждебности.

Все эти факты можно обобщить таким образом: если человек (или другое живое существо) готов увидеть связь между предметами или явлениями, он, скорее всего, ее увидит, даже если ее нет. Если же вы настроены не видеть эту связь, вы ее, скорее всего, не увидите, даже если она есть. Можно научить кошек тянуть за веревочку, чтобы выбраться из коробки. Но нельзя научить их вылизываться, чтобы это сделать. Собаки быстро поймут, что нужно идти вправо, а не влево, чтобы получить корм, если справа раздается звук из колонок; но очень трудно заставить собаку понять, что высокий тон означает, что еда находится справа, а низкий — что слева. Людям и животным кажется, что ориентировать в пространстве должны скорее пространственные подсказки, а то, что это может быть высота звука, понять трудно.

Уже известная нам эвристика репрезентативности порождает бесчисленное множество подготовленных зависимостей. Гениталии указывают на связь с сексом. Глаза символизируют подозрительность. Оружие связано с враждебностью. Эвристика доступности подливает масла в огонь, создавая еще больше подготовленных связей. В кино и мультфильмах у всяких сомнительных типов всегда подозрительный взгляд (например, человек смотрит искоса или у него бегают глаза).

А что, если человек не подготовлен ни к тому, чтобы увидеть связь, ни к тому, чтобы ее не увидеть?

Что произойдет, например, если человек слышит, как группа людей называет первую букву своего имени, потом они хором поют музыкальную ноту, а затем его спрашивают, есть ли какая-то связь между позицией этой буквы в алфавите и длительностью ноты?

Насколько высока должна быть корреляция между такими произвольно связанными событиями, чтобы люди гарантированно обнаружили ее?

Корреляция должна быть приблизительно равна 0,6 — чуть выше, чем корреляция 0,5, показанная на рисунке З. И это тогда, когда человек получает все данные сразу и изо всех сил старается понять, какая связь есть в данном случае. На деле это означает, что человек не может быть уверен, что между двумя величинами есть связь, если эта связь недостаточно сильна — она должна быть выше, чем многие из тех корреляций, на основе которых мы совершаем выбор в повседневной жизни. Чтобы сделать правильный вывод, нужно действовать систематически: наблюдать, записывать и делать расчеты, иначе окажется, что все ваши выводы — полная чушь.

Исключение

Точно распознать ковариацию очень трудно, но у этого правила есть одно важное исключение. Когда два события — даже сопоставленные преднамеренно — близки друг к другу по времени, ковариация обычно заметна. Если включать лампочку перед тем, как крыса получит удар электрическим током, крыса очень быстро заметит связь между светом и разрядом. Но даже когда речь идет о настолько явно связанных событиях, способность осознавать эту связь резко снижается с увеличением интервала времени между событиями. Ни животные, ни люди не улавливают связи между двумя намеренно связанными событиями, если интервал между ними превышает несколько минут.

Надежность и валидность

Много лет назад мой друг и его жена хотели завести ребенка. После нескольких лет безуспешных попыток они в конце концов решили посетить врача. Новости оказались невеселыми. В его сперме было «слишком мало сперматозоидов, чтобы оплодотворение произошло естественным путем». Друг спросил у врача, насколько надежен этот анализ. «Очень надежен», — ответил доктор. Он имел в виду, что анализ не бывает ошибочным — он дает верные данные. Это не слишком точное значение термина «надежный».

Надежность измерения переменной величины есть степень воспроизводимости того же результата от измерения к измерению или при переходе от одного метода измерения к другому.

Надежность измерения роста человека практически равна 1 (почти абсолютная корреляция при разных замерах). Надежность измерения IQ с интервалом в пару недель — примерно 0,9, а измерение IQ с помощью двух разных тестов обычно дает надежность более 0,8. Два стоматолога придут к согласию по поводу степени здоровья вашего зуба с надежностью менее 0,8. Это означает, что доктор Смит запломбировал бы вам зуб, а доктор Джонс оставил бы его как есть. Кстати, в другой раз решение того же стоматолога может быть иным, иначе говоря, в разных случаях между его решениями нет абсолютной корреляции. В пятницу доктор Джонс, возможно, запломбировал бы этот зуб, а во вторник не стал бы его сверлить.

Как же обстоит дело с подсчетом количества сперматозоидов? Надежность каждого конкретного метода анализа количества сперматозоидов невысока, как и надежность получения одинакового результата при разных способах измерения. При одновременном измерении количества сперматозоидов разными способами результаты могут быть совершенно разными.

Валидность (пригодность, обоснованность) метода обычно также измеряется с помощью корреляций. Валидность способа измерения означает меру его соответствия цели измерения. Валидность IQ-тестов обычно существенна — около 0,5, — в такой степени баллы теста на уровень IQ соответствуют среднему баллу школьного аттестата. (На самом деле именно потребность в прогнозировании успеваемости учеников побудила французского психолога Альфреда Вине в начале XX в. разработать первый тест на уровень IQ.)

Пожалуйста, не забывайте о чрезвычайно важном принципе: без надежности не может быть валидности. Если оценки, которые дает человек, нестабильны (нулевая корреляция между оценкой значения переменной А в одном и другом случае), значит, они непригодны и не подходят для прогнозирования значений переменной величины Б.

Если результаты теста X и теста У, которые должны измерить значения переменной величины, совпадают только случайно, тогда в лучшем случае лишь один из этих тестов сколько-нибудь валиден. Напротив, надежность может быть очень высокой даже при отсутствии валидности. Графологи утверждают, что могут по почерку определить степень честности, трудолюбия, амбициозности, оптимизма и множество других качеств человека. Два графолога могут сойтись во мнении о качествах человека (высокая надежность), но не могут предсказать реальное поведение человека в связи с качествами его характера (нулевая валидность).

Хотя анализ почерка порой может быть довольно полезен; например, для диагностики некоторых заболеваний центральной нервной системы.

Кодирование — ключ к статистическому мышлению

Я хочу, чтобы вы оценили в процентах корреляцию двух переменных величин. Схема всегда одинакова: насколько, по вашему мнению, вероятно, что А будет больше Б, если А была больше Б в другом случае? С помощью формул теории вероятностей ваши ответы легко преобразовать в коэффициенты корреляции.

Если вы ответите «на 50%» на один из вопросов, заданных ниже, это означает, что, на ваш взгляд, между поведением в одном и в другом случае нет никакой связи. Если вы скажете «на 90%», значит, вы считаете, что между поведением в одном и в другом случае существует чрезвычайно сильная зависимость.

Первый вопрос касается грамотности. Если вы полагаете, что количество орфографических ошибок в одном случае никак не зависит от количества ошибок в другом случае, отвечайте «50%». Если же вы считаете, что между тем, насколько грамотно вы пишете в одном конкретном случае и в любом другом, существует сильная связь, отвечайте «90%». Чтобы проверить себя — запишите свой ответ на каждый вопрос.

1. Если Карлос получит оценку за диктант выше, чем Крейг в конце первого месяца в 4-м классе, какова вероятность, что оценка Карлоса будет выше в конце третьего месяца?

2. Если Джулия забросила больше мячей, чем Дженнифер, в первых 20 баскетбольных играх сезона, какова вероятность, что она забросит больше мячей в следующих 20 играх?

3. Если при первом знакомстве Билл показался вам более дружелюбным, чем Боб, какова вероятность, что при второй встрече он вновь покажется вам более дружелюбным?

4. Если Барбара ведет себя честнее, чем Бет, в 20 ситуациях, свидетелем которых вы были (честно оплачивала счета, не хитрила, играя в настольные игры, честно говорила о ее оценках в школе и т.д.), какова вероятность, что Барбара будет вести себя честнее, чем Бет, и в следующих 20 ситуациях, которые вы увидите?

В таблице 4 представлены корреляции, соответствующие оценкам в процентах, которые вы только что сделали.

Мне уже известны ответы на эти вопросы, основанные на проведенных ранее исследованиях. Я знаю корреляцию между результатом первого и второго диктанта, а также корреляцию между средней оценкой по результатам 20 таких повторяющихся диктантов. Я знаю корреляцию между тем, какое впечатление производит человек при первой и при второй встрече, а также корреляцию между средним значением этих впечатлений в 20 подобных случаях и т. д.

Готов поспорить, что ваши ответы отражены в следующей таблице.

Таблица 4. Перевод оценок в процентах в коэффициенты корреляции

Оценка в процентах	Корреляция	Оценка в процентах	Корреляция
50	0	75	0,71
55	0,16	80	0,81
60	0,31	85	0,89
65	0,45	90	0,95
70	0,59	95	0,99

1. Судя по вашим ответам, вы считаете, что корреляция между результативностью игрока в 20 первых и 20 вторых баскетбольных матчах очень высока, и она выше, чем корреляция между оценками за диктант.

2. Судя по вашим ответам, вы считаете, что корреляция между дружелюбностью в одном и другом случае очень высока и практически так же высока, как корреляция между честностью в первых 20 и во вторых 20 ситуациях.

3. Ваши ответы означают, что, когда речь идет о чертах характера, корреляция выше, чем когда дело касается способностей.

В любом случае эта таблица отражает мнения студентов, принимавших участие в эксперименте, который я провел совместно с Зивой Кунда.

Посмотрите на рисунок 4. Заметьте, что предположения о поведении, отражающем способности людей (в сравнении с реальными данными о результатах баскетбольных игр и диктантов), близки к реальности. Корреляция между поведением (правильность написания диктанта или мячи, заброшенные за матч) в одной ситуации и в другой ситуации будет умеренно большая — примерно 0,5. И предположения по поводу взаимосвязи здесь оказались совершенно верными.

Этот пример также показывает, насколько важна роль закона больших чисел в расчете корреляций. Если посмотреть на сумму значений множества примеров поведения и сопоставить их с суммой значений другого множества примеров, корреляция будет значительно выше, чем для отдельных примеров поведения. Люди не могут определить, насколько выше корреляция, если примеров много, но они понимают, что примеры 20 случаев дают явно более точный прогноз следующих 20 случаев, чем один случай прогнозирует другой одиночный случай.

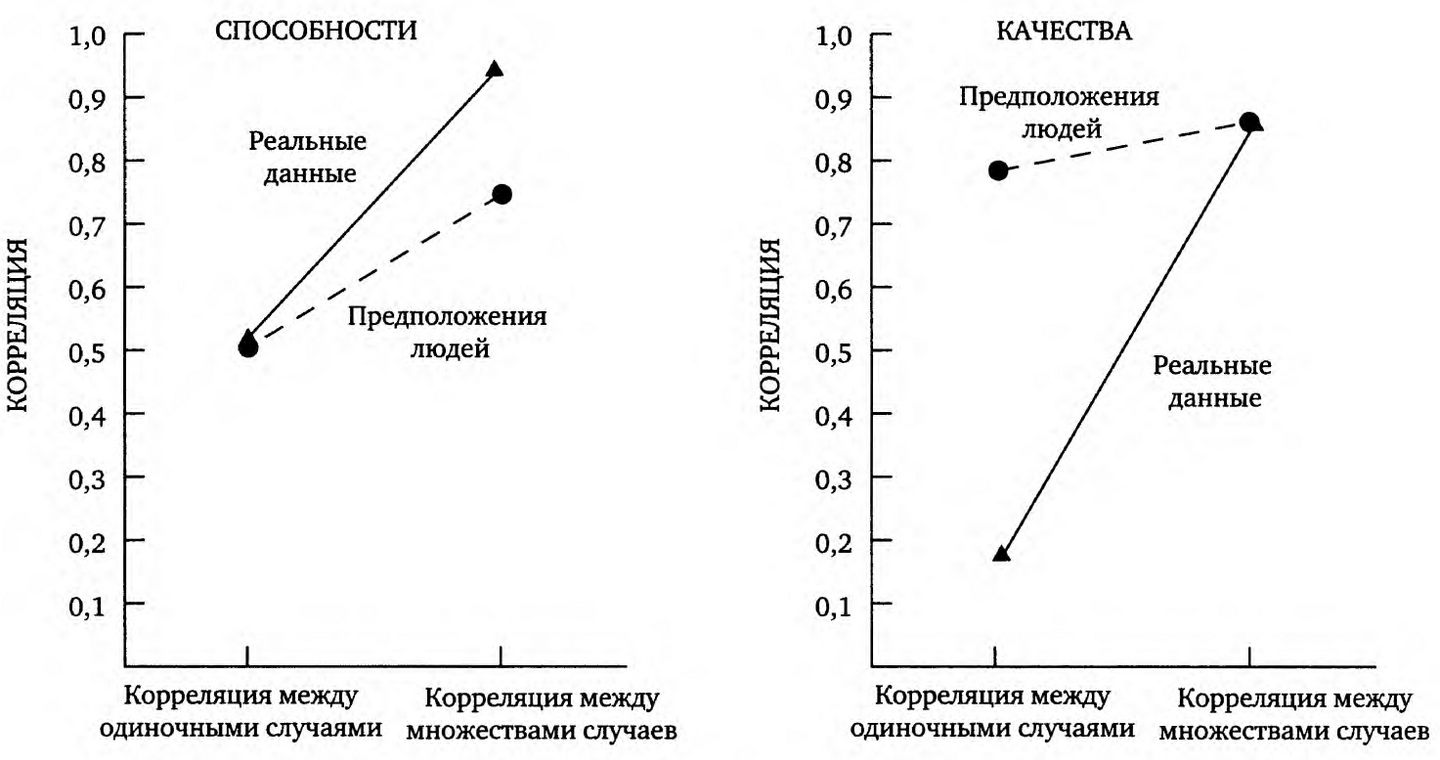
Рис. 4. Основанные на малых и больших объемах данных предположения о корреляции способностей человека (например, грамотности и умения играть в баскетбол) и качеств характера (например, дружелюбия и честности)

Сравните точность при анализе способностей с безнадежной неточностью при анализе свойств личности. Люди считают, что честность в одной ситуации коррелирует с честностью в другой ситуации, а дружелюбие в одном случае коррелирует с дружелюбием в другом случае до уровня 0,8! Это чудовищная ошибка. Как правило, корреляция между проявлениями поведения, отражающего какую-то черту личности, составляет 0,1 и меньше, и практически никогда не превышает 0,3. Здесь мы имеем дело с ошибкой, которая оказывает огромное и постоянное влияние на нашу жизнь, о чем уже говорилось в предыдущей главе. Мы думаем, что можем понять человека, увидев, как он ведет себя в ситуации, в которой проявляются определенные черты его личности. Эта ошибка неразрывно связана с фундаментальной ошибкой атрибуции, которая усугубляется нашей неспособностью признать, что закон больших чисел влияет на оценку личностных свойств точно так же, как он влияет на оценку способностей. Мы переоцениваем количество информации, которую извлекаем из небольшого примера поведения, потому что недооцениваем роль контекста, и к тому же уверены, что одного примера достаточно, чтобы предвидеть поведение человека в следующей, быть может, совершенно иной ситуации. Тот факт, что увеличение числа наблюдений делает выводы более эффективными, постоянно забывается. Если вы проанализируете поведение людей, отражающее черты их личности, на большом количестве примеров и сопоставите свои выводы с другими 20 случаями, вы получите действительно высокую корреляцию. Проблема в том, что люди полагают, что закон больших чисел при наблюдении за поведением, отражающим черты личности человека, работает и для небольшого количества примеров.

Почему уровень точности при оценке одиночных случаев, отражающих способности, и одиночных случаев, отражающих черты личности, радикально отличается? И почему роль закона больших чисел с готовностью признается при оценке способностей, но практически отрицается при оценке личностных качеств?

Все дело в кодировании. Когда речь идет о многих, если не всех, способностях, мы знаем, какие единицы измерения использовать, и можем перевести эти данные в числа (количество слов, написанных без ошибок; процент точных бросков за игру). Но в каких единицах измерить дружелюбность — в улыбках за минуту? В частоте положительных эмоций при общении? Как сравнить способы, которыми люди выражают дружелюбие на субботней вечеринке и на совещании в понедельник? Даже в этих двух типах обстоятельств люди ведут себя настолько по-разному, что знаки, которые мы воспринимаем как доказательства дружелюбия, в одной ситуации будут одни, а в другой — совсем другие. А уж пытаться перевести эти знаки дружелюбия в числовой эквивалент трудно или вовсе невозможно. Даже если мы могли бы перевести их в числа, мы не знали бы, как сравнивать индикаторы дружелюбия в ситуации А с индикаторами дружелюбия в ситуации Б.

Как же избежать ошибки в оценке личностных качеств? Мы не найдем точные единицы измерения и не сумеем дать им числовые значения. Психологи проделывают это в ходе исследований, но если бы мы с вами проводили подобные вычисления, мы бы ни с кем не смогли ими поделиться, потому что любой человек подумал бы, что мы сошли с ума. («Я даю Джону 18 баллов по шкале дружелюбности на совещании на основе общего количества улыбок, рассчитав соответствующее количество движений его губ. Подождите, не уходите! Куда вы?»)

Самый эффективный способ избежать неоправданно далекоидущих выводов о чьем-либо характере — напомнить себе, что поведение человека скорее всего будет одинаковым от случая к случаю только тогда, когда контекст ситуации совершенно одинаков. И даже в таком случае необходимо провести как можно больше наблюдений, чтобы быть уверенным в своем прогнозе.

Возможно, поможет также вспомнить, что вы сами не так уж чертовски последовательны. Я уверен, что люди, которые познакомились с вами в одних ситуациях, отзывались потом о вас как о милом дружелюбном человеке, а люди, которые видели вас в других ситуациях, посчитали вас совсем не милым и не дружелюбным. Кроме того, я уверен, что вы не обвинили бы этих людей в том, что они делают слишком поспешные выводы, принимая во внимание те сведения, что у них были. Просто помните, что то же самое верно и по отношению к тому парню, с которым вы только что познакомились. Нельзя утверждать, что он произвел бы на вас точно такое же впечатление в другой, возможно, совершенно иной ситуации, в которой вы могли повстречать его.

Говоря в более общем смысле, помните, что вы можете закодировать, а что нет. Если вы не можете навскидку закодировать или перевести в численный эквивалент значения данного события или поведения, попытайтесь придумать способ кодировки данного значения. Даже попытка сделать это, вероятно, станет для вас предупреждением, что вы рискуете переоценить систематичность события или поведения.

Есть и хорошая новость по поводу всего сказанного в этой и предыдущей главах. Мы говорили о методах статистики применительно к немногим и весьма узким сферам деятельности. Однако мой опыт показывает: даже нескольких примеров бывает достаточно, чтобы научить людей делать логические выводы из огромного количества событий, ничуть не напоминающих примеры из этой книги.

Когда я объясняю действие закона больших чисел на примере лотерей или подбрасывания монетки, то есть того, что в нашем представлении связывается со статистикой, мои слушатели начинают делать успешные умозаключения по поводу событий, о которых они не думают в вероятностном смысле, например об объективном измерении способностей. Как и о других явлениях, которые мы редко оцениваем в статистическом смысле, например о чертах личности. То же самое происходит, когда я призываю использовать только объективно измеряемые показатели способностей либо, наоборот, приводить субъективные, трудно поддающиеся измерению величины в качестве примеров. Когда человек учится решать задачи одного типа, он начинает лучше справляться с задачами совершенно иного типа.

Выводы

Точная оценка взаимосвязей может быть в вышей степени затруднительной. Даже если данные собраны и суммированы за нас, мы можем неверно оценить степень ковариации. Необъективность подтверждения — наиболее распространенная ошибка: если какие-то значения А равны значениям Б, этого может быть достаточно, чтобы мы посчитали, что А связано с Б. Но на самом деле, чтобы оценить, связано ли значение А со значением Б, необходимо сравнить две пропорции, составленные на основе четырехпольной таблицы.

Когда мы пытаемся оценить корреляции, которые никак не можем предсказать, например, когда мы пытаемся рассчитать корреляцию между бессмысленными или принужденно связанными событиями, корреляция должна быть очень высокой, чтобы мы смогли обнаружить ее. Наши способности к обнаружению ковариации оказываются очень слабыми, если события отделяет друг от друга больше, чем несколько минут.

Мы склонны к иллюзорным корреляциям. Когда мы пытаемся оценить корреляцию между двумя событиями, связь между которыми кажется правдоподобной, — то есть когда мы готовы найти положительную корреляцию между ними — мы решим, что такая корреляция присутствует, даже когда ее нет. Когда связь между событиями не кажется настолько правдоподобной, мы можем не заметить положительную корреляцию даже тогда, когда она есть и относительно высока. Еще хуже, если мы делаем вывод о наличии положительной корреляции, когда на самом деле она отрицательная, или о наличии отрицательной, когда на самом деле она положительная.

В основе многих наших изначальных предположений о корреляции лежит эвристика репрезентативности. Если величина А в чем-то похожа на величину Б, мы, вероятно, увидим взаимосвязь между ними. Эвристика доступности также может играть большую роль. Если первыми на ум приходят именно те случаи, где А связана с Б, а не те, где эта связь отсутствует, то нам свойственно сильно переоценивать степень этой взаимосвязи.

Корреляция не означает причинно-следственную связь, но когда существует правдоподобная причина, по которой А может являться причиной Б, мы склонны допустить, что корреляция означает причинноследственную связь. Корреляция между А и Б может возникнуть потому, что А является причиной Б, Б является причиной А либо что-то еще является причиной и того и другого. Мы постоянно упускаем из виду эти возможные варианты. Отчасти потому, что мы не осознаем, насколько легко «объяснить» корреляцию с точки зрения причинно-следственной связи.

Надежность измерения переменной величины означает степень воспроизводимости того же результата от измерения к измерению или при переходе от одного метода измерения к другому. Валидность (обоснованность) способа измерения показывает, насколько он прогнозирует то, что должен прогнозировать. Способ измерения величины может быть идеально надежным, но совершенно не валидным. Два астролога могут одинаково (надежно) оценивать, насколько люди, рожденные под знаком Рыб, более экстравертны, чем Близнецы, но их оценки никак не обоснованы.

Чем более кодируемы события, тем более вероятно, что наша оценка корреляций будет верна. Когда речь идет о легко кодируемых событиях, например о тех, которые обусловлены способностями человека, наша оценка корреляции между двумя фактами может быть довольно точной. Понятно и то, что среднее значение множества однотипных событий лучше прогнозирует среднее значение множества других событий того же типа, чем значение единичного события прогнозирует значение другого единичного события, когда эти события обусловлены способностями человека. И даже что касается способностей, мы и представить не можем, насколько прогнозирование, основанное на множестве наблюдений, точнее и качественнее прогноза, основанного на единичном наблюдении. Пытаясь оценить взаимосвязь трудно кодируемых событий, например поведения, которые определяются свойствами личности человека, мы можем далеко отклониться от истины, не понимая, насколько лучше наблюдение множества таких событий прогнозирует поведение человека, чем наблюдение отдельных случаев.

Если, исходя из прошлых поступков человека, мы пытаемся предсказать его поведение, основанное на его личностных свойствах, мы должны быть предельно осторожны и сдержанны, за исключением тех случаев, когда выборка случаев его поведения достаточно велика и наблюдалась в различных ситуациях с разнообразным контекстом. Сложность кодирования конкретных поступков говорит о том, что наши попытки прогнозировать поведение другого человека вполне могут быть ошибочными. Нужно постоянно напоминать себе, что концепция фундаментальной ошибки атрибуции помогает нам понять, когда и где мы делаем слишком далеко идущие выводы.

Назад: 7. Вероятность и объем выборки

Дальше: Часть IV. Эксперименты