В 2007 г. губернатор Техаса Рик Перри издал распоряжение, согласно которому всем девочкам по достижении 12 лет должны были делать прививки от вируса папилломы человека, заражение которым может привести к раку шейки матки. Критикуя Рика Перри в дебатах перед республиканскими выборами в 2012 г., кандидат Мишель Бахманн заявила, что одна женщина рассказала ей, что «ее дочке сделали эту прививку, а после этого у нее диагностировали задержку в умственном развитии».

Какая ошибка заключалась в выводе, сделанном Бахманн, — или по крайней мере в ее призыве сделать этот вывод — о том, что прививка от ВПЧ провоцирует умственную отсталость? Давайте подумаем.

Слова Бахманн нужно рассматривать как сообщение о примере инцидента, произошедшего среди представителей определенной популяции, а именно группы двенадцатилетних девочек из США, которым была сделана прививка против ВПЧ. Один случай умственной отсталости в этой популяции представляет собой слишком малую выборку (малое количество учтенных примеров), которой даже с натяжкой недостаточно для вывода, что здоровью этих девочек угрожают такие прививки.

Интересно, что на самом деле было проведено несколько опытов с произвольным распределением объектов по контрольным группам, в ходе которого экспериментаторы произвольно выбрали некоторых девочек для проведения прививок. Было обследовано огромное число девочек. Ни одно из исследований не показало, что среди девочек, которым была сделана прививка, количество умственно отсталых впоследствии оказалось выше, чем среди тех, кому прививку не сделали.

Приведенный Бахманн пример с прививкой является типичным образцом доверия статистике, основанной на источнике «я знаю одного человека, который сказал, что...». Пример Бахманн — в лучшем случае непродуманный, но никак не случайный. Чем больше процесс отбора образцов соответствует золотому стандарту случайного выбора — который означает, что каждый индивидуум данной популяции имеет равные шансы появления в выборке, — тем большего доверия он заслуживает. Если мы не знаем, случайно ли выбран данный пример, то любая статистическая оценка, которую мы дадим этому явлению, может оказаться необъективной.

Вообще-то пример Бахманн не назовешь непродуманным. Даже если предположить, что она говорила правду, у нее был серьезный мотив донести до общества именно этот случай. А может быть, она (либо ее информатор) говорила неправду. Причем это необязательно означает, что ее информатор лгала. Может быть, та женщина верила в то, что, как утверждается, она сообщила Бахманн. Если ее дочери сделали прививку, а затем диагностировали у нее задержку умственного развития, возможно, что вывод, сделанный матерью, является примером типичной логической ошибки «после этого — значит из-за этого». Тот факт, что событие 1 предшествует событию 2, еще не означает, что первое обязательно являлось причиной второго. В любом случае, мне кажется, мы должны понимать, что заявление Бахманн не дотягивает даже до статистики на уровне «Один Человек Сказал».

Один из моих любимых примеров логической ошибки «после этого — значит вследствие этого» в сочетании со статистикой «Один Человек Сказал» я знаю в изложении друга, который подслушал разговор между двумя пожилыми людьми. Первый сказал: «Врач говорит, чтобы я бросил курить, иначе умру». Второй ответил: «Нет! Не бросай! У меня двое друзей бросили курить, потому что им так сказали врачи, и оба умерли через несколько месяцев».

Вспомним пример с роддомами из главы 1, посвященной логическим выводам. В маленьких роддомах будет больше таких дней, когда количество родившихся мальчиков превысит 60% всех родившихся детей. Объясняется это действием закона больших чисел: выборочные значения, такие как средние значения и количественные соотношения, тем больше отражают реальные показатели внутри популяции, чем больше И, то есть объем выборки.

Действие закона больших чисел легко увидеть на примере большой популяции. Предположим, в роддоме за день родилось 10 малышей. Какова вероятность того, что 60% или более из родившихся детей мальчики? Разумеется, вероятность довольно высока. Мы ведь не удивимся, подбрасывая монетку, если орел выпадет 6 из 10 раз. Предположим, в другом роддоме за день родилось 200 детей. Насколько вероятным будет подобное отклонение от математического ожидания? Очевидно, что весьма маловероятным — как если бы подброшенная 200 раз монета упала орлом вверх 120 или больше раз, вместо ожидаемых 100 раз.

Попутно замечу, что точность выборочной статистики (средняя величина, медианное значение, среднеквадратическое отклонение и т.д.) по существу не зависит от размера популяции, из которой взята выборка. Для прогноза результатов общенациональных выборов опрашивают около 1,000 человек, и погрешность обычно находится в пределах ±3%. Выборка в 1,000 человек дает примерно одинаковый прогноз процентной поддержки кандидата при голосовании и 100 млн, и 10,000 человек. Так что, если ваш кандидат согласно результатам опросов опережает соперника на 8 баллов, не обращайте внимания на критические заявления соперников, что голосовать будут миллионы людей, а опросы охватывают всего тысячу. С одной оговоркой: если только люди, отобранные для опроса, не являются нетипичными представителями населения в каких-то важных аспектах. И тут мы вплотную подошли к вопросу ошибки выборки.

Закон больших чисел работает только для несмещенных выборок. Выборка оказывается смещенной (необъективной), если процесс ее составления допускает возможность того, что данное выборочное значение является ошибочным. Если вы пытаетесь выяснить, какое количество людей, работающих на заводе, хотели бы работать по гибкому графику, и опрашиваете только мужчин или только работниц столовой, мнение этих людей может значительно отличаться от мнения основного контингента работников. В целом это дает неверное представление о том, сколько работников завода хотели бы работать по гибкому графику. Если в выборке имеется смещение, то чем больше выборка, тем больше можно быть уверенным, что результат ошибочен.

Нужно отметить, что на самом деле выборка для опросов перед общенациональными выборами формируется вовсе не методом слепого отбора. Это было бы оправданно, если бы все избиратели в стране имели равные шансы попасть в выборку. Если это не так, вы рискуете получить серьезную ошибку выборки. Один из первых предвыборных опросов в США, проведенный журналом Literary Digest, показал, что Франклин Рузвельт проиграет выборы 1936 г., на которых на самом деле он одержал бесспорную победу. В чем была ошибка этого опроса? Он проводился по телефону, а в то время только очень обеспеченные люди (и большинство из них — республиканцы) имели дома телефон.

Нечто похожее произошло с некоторыми из предвыборных опросов, проведенных в 2012 г. Компания Rasmussen, проводившая опросы общественного мнения, не звонила на мобильные телефоны, игнорируя тот факт, что люди, у которых есть только мобильные телефоны и нет домашних, в большинстве своем молоды и чаще всего симпатизируют Демократической партии. Поэтому компания систематически переоценивала поддержку кандидата от Республиканской партии Митта Ромни по сравнению с результатами опросов путем звонков и на домашние, и на мобильные номера.

Когда люди отвечали на телефонные звонки и пускали в дом проводящих соцопросы, можно было достичь практически идеальной случайной выборки. В наши дни точность опроса зависит частично от данных, имеющихся у лиц, проводящих опросы, и интуиции, подсказывающей, какой лучше сделать выборку — подмешать ли в колдовское зелье из чисел вероятность, с какой респонденты пойдут голосовать, их симпатии той или иной партии, пол, возраст, статистику о том, как это сообщество или регион голосовали на прошлых выборах, глаз тритона или лягушачью лапку...

Рассмотрим следующие две задачи.

Университет А известен постановками мюзиклов в студенческом театре. Талантливые выпускники школ, от которых ждут больших успехов в будущем, могут получить стипендию на обучение в этом университете. Директор университетской театральной программы Джейн знакома с преподавателями актерского мастерства в окрестных школах. Однажды она отправляется посмотреть выступление ученицы, которую все преподаватели в один голос называют замечательной юной актрисой. Но на репетиции эта девушка несколько раз путает текст роли и, кажется, вообще неверно понимает характер своего персонажа. Да и особого сценического обаяния она не демонстрирует. Посмотрев репетицию, директор говорит своим знакомым, что теперь будет сомневаться в их оценках таланта их учеников. Верный это вывод или нет?

Джо подбирает игроков в футбольную команду университета Б. Он всегда ездит на тренировки школьных команд, если тренеры сообщают ему, что появился кандидат в университетскую сборную. Однажды он отправляется в школу, чтобы понаблюдать за нападающим, которого расхваливают его тренеры. Но на тренировке юноша промахивается, не может прорваться сквозь защитников и в целом не слишком результативен. В своем отчете начальству Джо пишет, что игрока переоценили, и рекомендует университету больше не рассматривать его в качестве кандидата в команду. Верное это решение или нет?

Если вы ответили, что Джейн приняла верное решение, а Джо нет, готов поспорить, что вы разбираетесь в спорте, но не в актерском мастерстве. Если же вы сказали, что Джо прав, а Джейн нет, вы, вероятно, разбираетесь в актерском мастерстве, но не в спорте.

Я обнаружил, что люди, которые мало понимают в спорте, чаще говорят, что Джо прав, заключив, что футболист не так уж талантлив, а люди, которые разбираются в спорте, считают, что Джон поторопился с выводом. Они допускают возможность, что выборка, представляющая собой единственную игру нападающего, была слишком мала и, возможно, это была худшая тренировка этого игрока. Таким образом, остается возможность, что способности этого спортсмена на самом деле гораздо больше соответствуют отзывам о нем, чем тому, что увидел Джо.

Люди, которые мало понимают в актерском мастерстве, скорее всего согласятся, что юная актриса не очень талантлива, но те, кто в этом разбирается, скажут, что Джейн пренебрежительно относится к суждениям своих друзей, преподающих в школе. При прочих равных условиях чем больше вы понимаете в каком-то вопросе, тем чаще можете применять статистические закономерности в своей работе. В данном случае важно помнить о законе больших чисел.

И вот почему здесь этот закон здесь необходим. Надежным показателем качества игры и уровня способностей футболиста можно считать то, как он играл на протяжении всего сезона или даже нескольких сезонов. Если его тренеры подтверждают эту информацию, настаивая на том, что он отличный игрок, это уже база доказательств — множество исходных данных, указывающих на то, что игрок, за которым наблюдал Джо, действительно талантлив. Результаты наблюдений Джо ничтожны по сравнению с наблюдениями тренеров, которые каждый день видят игрока на тренировках и в играх.

Конечно, уровень игры футболиста и даже целой команды может меняться от матча к матчу. Как гласит популярная присказка, в любое воскресенье любая команда Национальной футбольной лиги может победить любую другую команду Национальной футбольной лиги. Это не означает, что все команды одинаково сильны, просто нужно помнить: для того, чтобы с уверенностью судить об уровне команды, нужно увидеть много примеров ее игры.

Та же логика определяет мнение директора театральной программы о юной актрисе, выступление которой она смотрит. Если несколько человек, хорошо знающих эту девушку, говорят, что она талантлива, имеет смысл больше довериться их мнению, чем своему, основанному на недостаточном числе примеров. Однако мало кто признает это, за исключением тех, кто сам имеет за плечами сценический опыт и понимает, насколько разными могут быть выступления. Известный актер Стив Мартин писал в автобиографии, что почти любой комедийный актер может иногда сыграть великолепно. Но успех приходит к тем, кто умеет играть по меньшей мере неплохо — раз за разом.

Говоря языком статистики, тренер и директор театральной программы пытаются определить истинное значение кандидата, которого они наблюдают. Наблюдение = истинное значение + ошибка. Это верно для любых расчетов и исследований, даже если речь идет о росте людей или температуре воздуха. Повысить точность полученного значения можно двумя способами. Первый — усовершенствовать средства наблюдения, то есть найти линейки и термометры поточнее. Второй способ — «исключить» ошибки наблюдений, сколько бы их ни было, расширив выборку. Увеличьте количество наблюдений и найдите среднее значение на основе всех наблюдений в сумме. И не забывайте о законе больших чисел: чем больше сделано наблюдений, тем вы ближе к истине.

Даже когда мы высококомпетентны в какой-либо сфере и отлично разбираемся в статистике, мы можем забыть о концепции изменчивости и применении закона больших чисел. На факультете психологии Мичиганского университета для того, чтобы принять решение о приеме выпускника в аспирантуру, с ним проводят собеседование. Мои коллеги обычно придавали огромное значение итогам этой 20-30-минутной беседы с выпускником. «Не думаю, что она подойдет нам. По-моему, она не очень разбирается в вопросах, которое мы обсуждали». «Он выглядит очень уверенным в себе. Он рассказал о своей блестящей дипломной работе и сумел показать, что понимает, как проводятся исследования».

Проблема здесь в том, что суждения о человеке, основанные на малой выборке примеров поведения, могут «перевешивать» куда большее количество куда более важных свидетельств, включая средний балл аттестата колледжа, который отражает, как человек учился в течение четырех лет по тридцати с лишним академическим предметам; баллы за выпускной тест (GRE), который отражает знания, полученные за 12 лет обучения, и общие интеллектуальные способности; а также рекомендательные письма, которые обычно составляются на основе многих часов работы со студентом. На самом деле средний балл аттестата колледжа дает весьма приблизительное представление о том, как покажет себя этот студент в ходе последипломного обучения (корреляция здесь обычно будет примерно 0,3, что, как вы увидите из следующей главы, очень мало). Примерно такой же точности прогноз дают баллы, полученные за тест GRE. Два этих показателя в общем-то не зависят друг от друга, поэтому уровень точности совокупного прогноза по ним будет выше, чем по каждому из них по отдельности. Рекомендательные письма также повышают точность прогнозирования.

Для сравнения: совпадение прогнозов на основе получасового собеседования и последующей успеваемости кандидата на постдипломное обучение (и точно так же обстоит дело с офицерами, бизнесменами, будущими врачами, волонтерами Корпуса мира и другими людьми, проходящими подобное собеседование) обычно не достигает 0,1. Примерно с таким же успехом можно подбрасывать монетку. Все было бы не так плохо, если бы собеседование воспринимали так, как оно того заслуживает, — всего лишь как еще одну, завершающую попытку предвидеть результат. К сожалению, точность окончательного решения практически всегда снижается, поскольку значение собеседования преувеличивается по отношению к другой, более важной информации.

Значение собеседования настолько переоценивается, что этот короткий разговор может изменить мнение о человеке на прямо противоположное. Считается, что беседа с абитуриентом лучше расскажет о его успеваемости в университете, чем средние оценки в школе, а о готовности к работе в Корпусе мира — лучше, чем рекомендательные письма, основанные на многочасовом наблюдении за кандидатом.

Давайте расставим все точки над i по поводу информации, которую дает собеседование. В том случае, если у вас есть значимая, безусловно ценная информация о претенденте на место, которую можно узнать, просто просмотрев его бумаги, тогда лучше не проводить собеседование вообще. Если бы мы умели придавать собеседованию ровно столько значения, сколько оно заслуживает, это было бы не так, но не переоценивать его значение практически невозможно, потому что мы склонны с неоправданной самоуверенностью относиться к собственным наблюдениям, которые якобы дают нам верное представление о способностях и качествах человека.

Результаты собеседования надо воспринимать как голографический снимок человека — изображение меньше, оно расплывчатое, но все же это изображение этого человека. Собеседование — это крохотный, фрагментарный и, возможно, искаженный пример, вырванный из контекста всей информации, которая имеется об этом человеке. Вспомните буддистскую притчу про слона и слепых и заставьте себя поверить, что вы и есть один из этих слепых.

Помните, что иллюзия важности собеседования и фундаментальная ошибка атрибуции (ФОА) —явления одной природы. То и другое усугубляется тем, что нам никогда не удается уделить нужное количество внимания той информации, которая имеется о человеке. Если бы мы лучше понимали смысл ФОА, мы бы гораздо больше сомневались в той информации, которую дает собеседование. Точное применение закона больших чисел также делает нас менее подверженными ФОА и иллюзии собеседования.

Я бы хотел с гордостью заявить, что мои знания об истинной пользе собеседований всегда позволяют мне критически относиться к собственным умозаключениям, сделанным на основе собеседования. Однако сдерживающий эффект здесь весьма и весьма ограничен. Слишком сильна иллюзия, что я обладаю ценными знаниями, имеющими под собой серьезную основу. Все равно приходится напоминать себе, что я не должен придавать слишком большое значение собеседованию или любому другому поверхностному впечатлению о человеке. Это особенно важно, когда я обладаю заведомо надежной информацией о нем, основанной на мнении других людей, давно знающих кандидата, а также подробным перечнем достижений этого человека в научной или другой области.

Однако мне не составляет труда помнить об ограниченности чужих суждений, основанных на коротком собеседовании!

Моя подруга — назовем ее Кэтрин — консультирует руководство медицинских учреждений по вопросам менеджмента. Она любит свою работу— отчасти потому, что ей приходится путешествовать и знакомиться с людьми. Кроме того, она немного гурман и любит ходить в хорошие рестораны. Но часто разочаровывается, вновь посетив понравившееся заведение. Во второй раз еда уже не кажется ей такой вкусной. Как вы думаете почему?

Если вы ответите «Может быть, потому что в этом ресторане часто меняется шеф-повар» или «Вероятно, у нее завышенные ожидания», вы игнорируете кое-какие важные статистические закономерности.

Статистический подход к проблеме начинается с понимания того факта, что в том, насколько вкусную еду приносят Кэтрин в любом конкретном ресторане в каждом конкретном случае, всегда содержится элемент случайности. В зависимости от обстоятельств вашего визита в ресторан вы будете по-разному оценивать качество поданных блюд. Блюдо, которое Кэтрин попробовала в этом ресторане первым, по качеству могло варьировать от среднего (или даже ниже среднего) до великолепного. Эта разница и заставляет нас относиться к качеству оцениваемой еды как к переменной величине.

Непрерывная переменная величина (которая может непрерывно изменяться в диапазоне от наименьшего до наибольшего значения — как, например, рост людей), в отличие от дискретной переменной (например, в случае с гендерной идентификацией или политическими пристрастиями), всегда имеет среднее значение и распределение относительно среднего значения. Принимая во внимание один этот факт, неудивительно, что Кэтрин часто была разочарована: нельзя избежать вероятности, что иногда второй поход в ресторан окажется хуже, чем первый (точно так же, как в некоторых случаях второй раз оказывается лучше первого).

Но это еще не все. Следует ожидать, что мнение Кэтрин о блюде, которое однажды показалось ей превосходным, ухудшится. Это происходит оттого, что чем ближе переменная величина к своему среднему значению, тем чаще она встречается. Чем она дальше от среднего значения, тем она встречается реже. Поэтому если в первый раз еда показалась ей исключительной, то в следующий раз, вероятно, ее оценка будет не такой. Это верно для так называемого нормального распределения, график которого изображается кривой нормального распределения, показанной на рисунке 2.

Нормальное распределение — это математическая абстракция, но к ней на удивление часто стремится «поведение» непрерывных переменных величин. Например, количество яиц, которые еженедельно откладывают разные курицы; количество ошибок при сборке автомобильных коробок передач за месяц; результаты теста разных людей на IQ — все эти значения часто приближаются к нормальному распределению. Никто не знает почему, но это так.

Существует несколько способов описать дисперсию (разброс, отклонение) значений переменной от ее среднего значения. Один из них — подсчитать размах выборки — разность наибольшего и наименьшего значений. Другой, более эффективный способ измерения дисперсии — метод среднего отклонения от среднего значения. Если среднее качество блюд, которые попробовала Кэтрин при первом посещении ресторанов, обозначить как, скажем, «хорошее», а среднее отклонение от среднего значения равняется, скажем, «очень хорошему» в положительную сторону и «весьма посредственному» в отрицательную сторону, мы можем сказать, что степень дисперсии — среднего отклонения мнения Кэтрин о блюдах, которые она впервые пробует в ресторанах, не очень велика. Если же среднее отклонение варьирует от «великолепного» в положительную сторону до «весьма посредственного» в отрицательную сторону, то можно сказать, что дисперсия довольно велика.

Но есть еще более действенный способ вычисления дисперсии, который можно применить к любой непрерывной переменной величине. Это среднеквадратическое отклонение, оно же СКО, обозначаемое греческой буквой σ (сигма). Среднеквадратическое отклонение — это квадратный корень из дисперсии переменной величины. В принципе, среднеквадратическое отклонение не слишком отличается от среднего, но обладает кое-какими чрезвычайно полезными свойствами.

На кривой нормального распределения на рисунке 2 отмечены среднеквадратические отклонения. Примерно 68% значений переменной находятся в пределах от +σ до -σ (от плюс одного до минус одного стандартного отклонения от среднего значения выборки). Возьмем, например, результаты теста на IQ. В большинстве IQ-тестов средним значением принято считать 100 баллов, а среднеквадратическим отклонением — 15. То есть человек с уровнем IQ, равным 115, является среднеквадратическим отклонением выше среднего значения. Расстояние между средним значением и среднеквадратическим отклонением выше среднего довольно велико. Можно ожидать, что человек с IQ, равным 115 баллам, окончит университет и даже займется научной работой. Люди с таким уровнем IQ обычно получают высшее образование и становятся специалистами в какой-то области, менеджерами или инженерами. Люди с уровнем IQ, равным 100 баллам, чаще получают среднее специальное образование или вообще нигде не учатся после школы и становятся продавцами, секретарями или рабочими.

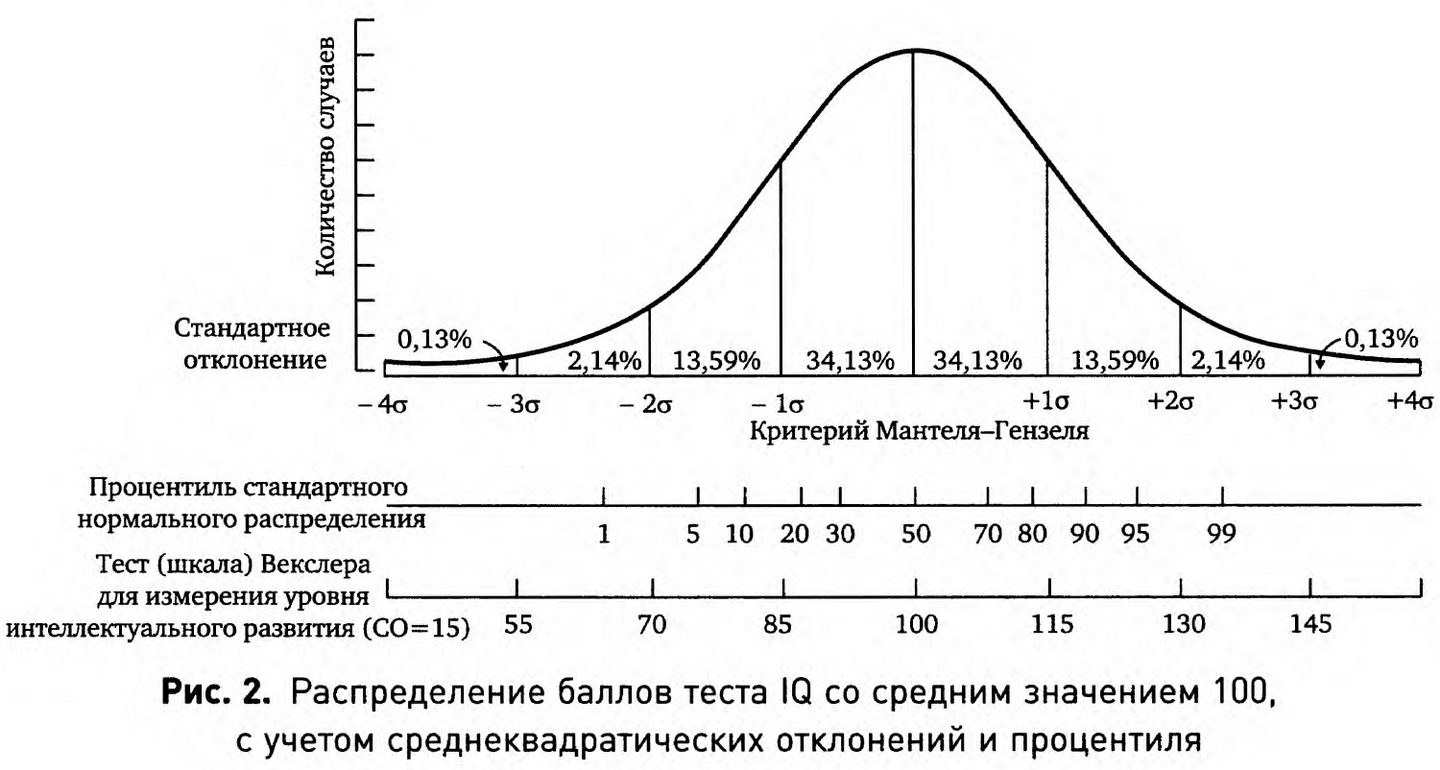
Еще один набор полезных фактов о среднеквадратическом отклонении касается соотношения между процентилями (сотыми частями распределения, выстроенными в ряд по их величине) и среднеквадратическими отклонениями. Примерно 83% наблюдаемых случаев имеют менее одного среднеквадратичного отклонения, превышающего среднее значение. Наблюдение с одним СКО от среднего значения находится в 84% распределения. Оставшиеся 16% наблюдаемых случаев превышают 84 процентиля. Почти 98% количества всех наблюдений содержат менее двух СКО выше среднего значения. Ровно два СКО от среднего значения входят в 98%. Всего 2% оставшихся наблюдаемых случаев превышают это значение. Почти все наблюдения окажутся между тремя СКО ниже среднего значения и тремя СКО выше среднего значения.

Знание соотношения между среднеквадратическими отклонениями и процентным выражением помогает судить о большинстве непрерывных переменных величин, с которыми мы сталкиваемся. Например, расчет среднеквадратического отклонения часто используется в финансовой сфере. Среднеквадратическое отклонение уровня дохода на инвестиции определяет уровень нестабильности инвестиций. Если пакет акций в среднем приносит 4% прибыли за последние десять лет с среднеквадратическим отклонением 3%, это означает, что наиболее вероятным предположением будет то, что 68% времени в будущем уровень прибыли составит от 1 до 7% и 96% времени доход будет больше, чем -2%, и меньше 10%. Это довольно стабильно. Такой доход не сделает вас богачом, но и нищим вы тоже не будете. Если среднеквадратическое отклонение равно восьми, это означает, что 68% времени уровень дохода будет между -4 и +12%. Этот пакет акций может действительно принести хорошую прибыль. 16% времени вы будете получать более чем +12% прибыли. В то же время, 16% времени вы будете терять более чем 4%. Это весьма нестабильно, 2% времени вы будете зарабатывать более чем 20%. Можно разбогатеть, а можно и остаться без гроша.

Так называемые устойчивые акции обладают высокой стабильностью как относительно дивидендов, так и относительно цены. Они могут приносить 2, 3, 4% прибыли каждый год и, вероятно, не слишком поднимутся в цене при растущем рынке, но также и не слишком упадут в цене в ситуации, когда цены на рынке снижаются. Так называемые акции роста обычно приносят прибыль с более высоким среднеквадратическим отклонением, что означает более высокий потенциал роста наряду со значительно более высоким риском падения курса.

Финансовые консультанты обычно советуют молодым клиентам выбирать акции роста и продержаться в те периоды, когда цены падают, потому что в долгосрочной перспективе акции роста все-таки растут — хотя периоды падения могут быть утомительно долгими. Клиентам постарше консультанты чаще советуют выбирать более устойчивые акции, чтобы момент выхода на пенсию не совпал с периодом падения курса.

Что интересно — все, что вы только что прочитали про нормальное распределение, существует независимо от формы нормального распределения, которая лишь иногда похожа на кривую распределения. В разных случаях это разные кривые эксцесса. Это может быть островершинная кривая с положительным эксцессом, напоминающая ракету из комиксов 1930-х гг. с острой вершиной и короткими хвостами. Это может быть плосковершинная кривая с отрицательным эксцессом, напоминающая удава, проглотившего слона, с низкими вершинами и низкими хвостами. Тем не менее для обоих распределений 68% всех значений находятся в пределах от плюс до минус одного среднеквадратического отклонения.

Но вернемся к вопросу о том, почему Кэтрин обычно разочаровывается, вернувшись в ресторан, где ее отлично кормили в первый раз. Мы пришли к выводу, что ее оценка ресторанных блюд является переменной величиной: она варьирует, скажем, от «отвратительно» (1-й процентиль) до «божественно» (99-й процентиль). Предположим, что великолепные блюда относятся приблизительно к 95-му процентилю или даже выше — то есть это лучше 94% блюд, которые ей подают в ресторанах. А теперь спросите себя, вспомнив собственный опыт, — что кажется вам более вероятным: что каждое блюдо, которое вы съедите в ресторане, где никогда не бывали раньше, окажется великолепным или что великолепными окажутся только некоторые из них? Если вы полагаете, что не следует ожидать, что все блюда будут великолепными, но вам повезло и в первый раз в ресторане вам приносят именно такое блюдо, то ожидаемое значение второй (следующей) величины должно быть как минимум немного ниже, чем первой.

Опыт Кэтрин с посещением ресторанов во второй раз можно представить как регрессию к среднему значению. Если впечатления от блюд, попробованных в ресторанах, распределяются нормально, то предельные (крайние) значения по определению маловероятны, поэтому случай данного вида, следующий за предельным случаем (крайностью), как правило, оказывается менее предельным. Предельные случаи регрессируют до менее предельных.

Эффект регрессии легко увидеть повсюду в нашей жизни. Почему лучший молодой игрок бейсбольной команды этого года так часто разочаровывает своей игрой во втором сезоне? Регрессия. Показатели этого игрока в первый год были аномально высокими по сравнению с его обычными результатами, и у него нет другого пути, кроме как вниз. Почему акции, выросшие в цене больше, чем какие-либо другие, в этом году дают весьма средний доход, если не падают вообще, на следующий год? Регрессия. Почему ребенок, который учился хуже всех в третьем классе, вдруг начинает учиться немного лучше на следующий год? Регрессия. Однако ни один из этих примеров не представляет собой чистую регрессию и ничего больше. Среднее значение распределения — это не черная дыра, которая затягивает в себя все крайние наблюдаемые значения. На снижение или повышение показателей может повлиять множество факторов. Но, не зная точно, что это за факторы, необходимо признать, что за предельными значениями обычно следуют менее предельные значения, потому что сочетание всех факторов, которые привели к предельному значению, как правило, не может оставаться неизменным в течение длительного времени. Новому игроку команды посчастливилось иметь тренера, у которого также выдался необычайно продуктивный сезон; в первых матчах он играл против относительно слабых соперников, что придало ему уверенности в своих силах; он только что обручился с девушкой своей мечты; у него было идеальное здоровье; у него не было травм, которые могли бы повлиять на игру, и т.д. А на следующий год ему пришлось пропустить несколько матчей из-за вывихнутого локтя; в команду пришел новый тренер; в семье кто-нибудь заболел. Да что угодно. В жизни всегда что-нибудь случается.

Вот два вопроса, на которые нужно отвечать, используя принцип регрессии (как это ни странно):

Вероятность, что человек войдет в 1% людей с самым высоким доходом, составляет 110 на 1000. Готов поспорить, что сами вы бы не догадались. А вот вероятность, что человек останется на этом же уровне в течение десяти лет, составляет всего 6 на 1000. Поразительно на фоне вероятности разбогатеть на один год. Эти данные особенно удивляют потому, что мы не думаем о доходе как о величине в высокой степени переменной и подверженной эффекту регрессии. Но на самом деле изменчивость доходов индивида от года к году очень велика (особенно это касается распределения доходов в верхнем сегменте). Предельные значения доходов, как ни странно, широко распространены среди населения в целом. Но именно потому, что они предельные, они не часто будут повторяться из года в год. Подавляющее большинство этих злополучных богачей из 1% уже скоро не будут в него входить, так что не слишком завидуйте им!

Тот же самый принцип можно применить к предельно низким доходам. Более 50% американцев оказывались за чертой бедности или крайне близко к ней хотя бы раз в своей жизни; но вовсе не так много людей живут за чертой бедности постоянно. Редко можно встретить человека, который постоянно сидит без работы. Большинство тех людей, которые когда-либо в своей жизни жили на социальное пособие, жили на него максимум пару лет или около того. Так что не принимайте и их слишком близко к сердцу.

Мы можем наделать серьезных ошибок, неправильно истолковав событие в смысле возможности регрессии к среднему значению. Психолог Даниэль Канеман, беседуя с группой израильских авиаинструкторов, сказал однажды, что похвала более эффективна, чем критика, если нужно изменить чье-то поведение в желательном направлении. Один из инструкторов возразил, сказав, что, если похвалить пилота за хорошо выполненный маневр, в следующий раз он выполнит его хуже, а вот если наорать на него за плохой маневр, то в следующий раз он выполнит его лучше. Однако этот инструктор не заметил тот факт, что показатели работы неопытного пилота нестабильны и после очень хороших полетов следует ожидать регрессию к среднему значению — как и после очень плохих полетов. Исходя из чистой теории вероятностей можно ожидать, что после полета, прошедшего лучше, чем обычно, последует полет, более близкий к средним показателям, то есть он будет хуже. Если же полет прошел хуже обычного, следует ожидать улучшения в последующие разы.

По всей вероятности, показатели учеников этого инструктора были ниже, чем могли быть, если бы он воспринимал эти показатели как непрерывную переменную величину и ожидал, что за любым предельным значением обязательно последует значение менее предельное. В таком случае он бы только поощрял выдающиеся успехи своих учеников, что позволило бы ему вырасти как учителю.

Восприятие — обоюдоострый меч, который мы всегда носим с собой, — дает мощный импульс такой ошибке инструктора. Мы все мастера сочинять гипотезы о причинах тех или иных событий. Узнав о событии, мы проявляем завидную находчивость, объясняя его причины. Увидев разницу в наблюдениях на протяжении длительного времени, мы с готовностью выдаем интерпретацию причин этих различий. Большую часть времени причинные связи отсутствуют вообще — а есть лишь случайные совпадения. Когда мы начинаем замечать, что какое-то событие постоянно происходит в связке с другим событием, желание дать этому объяснение становится поистине непреодолимым. Наличие такого соотношения событий почти автоматически провоцирует на нас на соответствующие выводы и объяснение причин. Конечно, полезно быть все время начеку, ища причинно-следственные связи, объясняющие, почему в мире все происходит так, а не иначе. Но тут возникают две проблемы: 1) объяснения даются нам слишком легко — если бы понимали, насколько поверхностны наши гипотезы о причинно-следственных связях, мы бы доверяли им намного меньше; 2) в большинстве случаев никакая причинно-следственная интерпретация не подходит вообще, и нам даже в голову не пришло бы ее выдумать, если бы мы лучше понимали, что такое случайный характер явлений.

Если вы ответили, что ожидаемое значение уровня IQ ребенка — с учетом того, что IQ одного родителя 140, а другого 120, — будет 140 или выше, вы не учли феномен регрессии к среднему значению. IQ, равное 120, это уровень выше среднего, как и 140. Если вы не думаете, что между IQ родителей и ребенка возникает идеальное соотношение, вы должны спрогнозировать, что IQ ребенка будет ниже, чем среднее значение IQ его родителей. Так как соотношение между средними значениями IQ обоих родителей и среднее значение IQ ребенка равно 0,50 (чего вы, полагаю, не знали), ожидаемая величина IQ ребенка окажется где-то посередине между средним значением этой величины у родителей и средним значением всего населения в целом, а именно 115. У очень умных родителей родятся дети, которые будут просто умны (выше среднего уровня). У очень умных детей обычно родители, которые просто умны (выше среднего уровня). Регрессия работает в обоих направлениях.

Эффект «до и после» обычно объясняют тем, что пациенты притворяются, что им хуже, чем на самом деле, чтобы было видно, что они нуждаются в лечении. Но к концу лечения им хочется снискать расположение лечащего врача. Независимо от того, насколько это объяснение правдиво, мы ожидаем улучшения состояния пациента в конце лечения, а не в начале, потому что эмоциональное состояние пациента в то время, когда они ожидают лечения, вероятно, также хуже, чем обычно, и потому что сам по себе тот факт, что время идет, вызывает регрессию к среднему значению. Этот эффект проявляется даже при отсутствии лечения вообще.

Кстати говоря, время работает на врачей: со временем пациент ожидаемо идет на поправку, конечно, за исключением случаев, когда болезнь прогрессирует. Поэтому, каким бы ни было врачебное вмешательство, у него всегда будут шансы считаться действенным. «Я съела суп из одуванчиков, и простуды как не бывало». «Моя жена выпила отвар столетника, как только заболела гриппом, и у нее все прошло в два раза быстрее, чем у меня». Статистика «Один Человек Сказал» в сочетании с эвристическим правилом «после этого — значит вследствие этого» помогла разбогатеть многим производителям чудодейственных средств от всех болезней. И они не соврут, утверждая, что большинство людей почувствовало себя лучше после того, как приняли их лекарство.

Но я немного забегаю вперед, говоря о регрессии. Мы незаметно перешли от закона больших чисел к обсуждению концепции ковариации или корреляции. А это тема следующей главы.

Зачастую наблюдения за объектами или явлениями должны восприниматься как примеры выборки. Качество еды в конкретном ресторане в конкретный день, качество игры конкретного спортсмена в конкретной игре, сколько раз шел дождь за ту неделю, которую вы провели в Лондоне; приятно ли вам общество человека, с которым вы встретились на вечеринке, — все это нужно рассматривать лишь как выборку из огромного общего количества примеров. И любая оценка, подходящая к данной переменной величине, будет в той или иной степени ошибочна. Чем больше выборка, тем (при прочих равных составляющих) больше вероятность, что ошибки станут взаимоисключающими и мы приблизимся к правильному ответу. Закон больших чисел применяется к тем событиям, количество которых сложно определить, равно как и к тем, которые достаточно легко закодировать таким образом.

Фундаментальная ошибка атрибуции изначально возникает из-за нашей склонности игнорировать ситуационные факторы и осложняется тем, что мы отказываемся признавать тот факт, что короткое знакомство с человеком представляет собой лишь крохотную выборку его поступков. Иллюзия собеседования также основана на ошибке — увидев, как человек говорил и вел себя на получасовой беседе, мы по своей самоуверенности воображаем, что знаем, что он из себя представляет.

Увеличение выборки уменьшает ошибки только в том случае, если выборка является несмещенной (объективной). Добиться этого можно, предоставив каждому явлению, событию или человеку из данной популяции равные шансы участия в выборке. Нужно с вниманием относиться к опасности смещения выборки: отдохнул ли я, сходив в ресторан с женой, или был напряжен, потому что с нами была ее сестра, которая вечно всех критикует? А использовав расширенную смещенную выборку, можно лишь еще больше утвердиться в своем ошибочном выводе.

Среднеквадратическое отклонение — это простой способ измерения дисперсии непрерывной переменной величины относительно среднего значения. Чем больше среднеквадратическое отклонение в наблюдении данного типа, тем меньше мы можем быть уверены, что конкретное наблюдение будет близко к среднему значению, верному для всей выборки. Большое среднеквадратическое отклонение для инвестиции означает, что ее доходность окажется под вопросом.

Если мы знаем, что наблюдение переменной величины определенного вида относится к предельным значениям распределения этой переменной, то очень вероятно, что результаты последующих наблюдений не будут предельными. Студент, получивший высший балл на последнем экзамене, вероятно, хорошо сдаст следующий экзамен, но вряд ли снова получит высший балл. Акции десяти компаний, занимавшие самые высокие позиции в прошлогоднем рейтинге, не останутся на тех же позициях в этом году. Предельные значения стали предельными, потому что так расположились звезды (или не расположились). В следующий раз звезды, скорее всего, поменяют свое положение.