1.2. НОРМАЛЬНЫЙ ЗАКОН РОСТА НАСЕЛЕНИЯ - Русский Холокост. Истоки и этапы демографической катастрофы в России - Михаил Васильевич Матосов - RutLib.com

1.2. НОРМАЛЬНЫЙ ЗАКОН РОСТА НАСЕЛЕНИЯ

При анализе данных о росте народонаселения в любом государстве обнаруживается интересная общая закономерность: при стабильных внешних и внутренних условиях численность населения растет вполне определенным образом. Чтобы ее пояснить, обозначим через N численность населения в данный момент времени t, а через ΔN – прирост населения за интервал времени At.

Нормальный закон роста населения при стабильных условиях утверждает:

Скорость прироста населения, т. е. отношение прироста населения Δ N к промежутку времени Δ t, пропорциональна величине населения N.

Понять такой закон несложно: чем больше население страны, тем больше будет прирост этого населения, например, за год, и тем выше скорость роста населения. А значит, численность населения в какой-то стране при нормальных условиях растет, все время убыстряясь. В математике такую зависимость называют экспоненциальной, она приведена на рис. 1.. Ее нелинейность затрудняет сравнение чисел между собой. Удобно представить численность населения N в логарифмическом масштабе, т. е. откладывать по оси значение IgN. В этом случае зависимость значений численности населения от времени будет линейной и удобной для анализа (рис. 2).

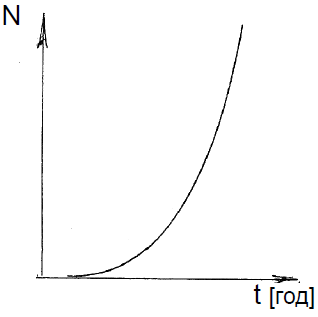
Рис. 1

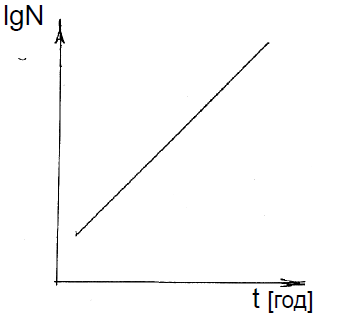
Рис. 2

Тит

Смешно , читать , что еврейское происхождение стало главной причиной отказа Троцкого от жесткой борьбы за власть . А вокруг его в верхушке парти были кто ? А почему это происхождение совершенно не мешало Ленину -внуку одесского равина? Или быть может в ЦК партии заседали одни черносотенцы -антисемиты ? Или же они собирались избирать главу диктатуры пролетариата на всенародных выборах , а не среди ЦК и на съезде , где абсолютное большинство имело тоже самое происхождение просто может быть более скрываемое и более зашифрованное ? Но почему всем другим оно не мешало занимать ответственные посты в партии и правительстве , а даже наоборот служило лучшей рекомендацией ? Очевидно , что это самое нелепое объяснение , по все видимости выдуманное и притянутое за уши учитывая тот факт что Сталин тоже был инородец к тому же разговаривший с заметным акцентом в отличае от Троцкого . Поэтому пересказывать эту клюкву снова и снова всерьёз это показывать свою наивность .

Тит

Да , очевидно , что Троцкого сгубило высокомерие и ощущение собственного превосходства над всеми другими , которое убаюкало его в ответственный момент , когда Ленин умер .Недаром все последующие наследники умирающих вождей считали обязательным не просто участвовать в похоронах , но и возглавлять комиссию по похоронам . По все видимости на верху политбюро это считалось главной ошибкой Троцкого и в последующем это соблюдалось как закон - кто хоронит тот и наследует . В этом конечно , что то он наследственной монархии , что совершенно не соответствует марксискому и демократическому духу . И видимо поэтому Троцкий принебрег участием в похоронах , но получилось это слишком демонстративно и видимо сыграло свою роль как демонстрация отдаленности Троцкого от партии . Что и сгубило его , когда все партийные бонзы отвернулись от него и он проиграл несмотря на поддержку и веру в него среди рядовых активистов . Его свергла именно верхушка . И видимо сплочению Ее против него послужило именно не участие и дестанцирование на похоронах . А вот чем это могло быть вызвано не понятно . Врядли он не знал , что Ленин плох и присмерти , если нет доказательств обратному в виде письменных свидетельств заверяющих его уверенность в стабильности положения Ленина . Если такие свидетельства есто то тогда версия об отравлении Ленина вовремя может иметь право на жизнь . А вот если он знал что Ленин присмирит и специально удалился из Москвы на окраину , то на это должны быть другие причины . Как то может быть личная неприязнь к Ленину из-за соперничества и нежелание его хоронить или ожидание , что после смерти начнётся восстание .