Книга: Чёрный лебедь. Под знаком непредсказуемости
Назад: Глава 14. Из Среднестана в Крайнестан и обратно
Дальше: Глава 16. Эстетика случайности
Глава 15. Кривая нормального распределения, великий интеллектуальный обман
Не стоит рюмки ликера. — Ошибка Кетле. — Средний человек — чудовище. —Давай обожествим ее. —Да или нет. —Не такой буквальный эксперимент
Забудьте всё, что вам рассказывали в колледже про статистику и теорию вероятности. Если вы никогда не слушали такого курса лекций, еще лучше. Начнем с самого начала.
ПО ГАУССУ И ПО МАНДЕЛЬБРОТУ
В декабре 2001 года, по пути из Осло в Цюрих, я делал пересадку во Франкфурте.
Нужно было как-то убить время в аэропорту, и мне представился отличный повод купить темного европейского шоколада и даже убедить себя, что транзитные калории в организме не задерживаются. Кассир дал мне, помимо прочего, банкноту в 10 немецких марок, которую (нелегально отсканированную) вы можете увидеть на следующей странице. Через несколько дней немецкие марки должны были выйти из обращения, так как Европа переходила на евро. Я сохранил банкноту на память. Перед приходом евро в Европе было множество национальных валют, что было хорошо для печатников, обменных пунктов и, конечно, валютных трейдеров, таких как ваш (более или менее) покорный слуга. Я жевал темный европейский шоколад, с грустью глядя на банкноту, — и вдруг чуть не подавился. Я заметил на ней (впервые!) кое-что весьма примечательное. На банкноте был портрет Карла Фридриха Гаусса и изображение... его кривой нормального распределения.
Вся ирония в том, что более неподходящего изображения, чем "гауссова кривая", для данной немецкой банкноты не придумаешь: в 20-е годы рейхсмарка (так эта валюта называлась раньше) упала с четырех за доллар до четырех триллионов за доллар всего за несколько лет, то есть очевидно, что колебания курса валют не описываются кривой нормального распределения. По-моему, метаморфозы, произошедшей с рейхсмаркой, было более чем достаточно, чтобы больше не допускать гауссиану на денежные знаки. Но на моей банкноте была именно она, гауссиана, и рядом с ней герр профессор, доктор Гаусс, невозмутимый, немного суровый человек, с которым я едва ли захотел бы, развалившись в шезлонге и попивая ликер, поболтать о том о сем.

Но представьте, солидные управляющие в крупнейших банках, которые носят строгие темные костюмы и с важным видом обсуждают поведение валют, вовсю пользуются "гауссовой кривой" как инструментом для измерения риска. Ужас!
Нарастание убывания
Основной принцип "гауссовой кривой", позвольте напомнить, состоит в том, что большинство наблюдений относится к заурядности, к среднему; по мере того как вы отдаляетесь от средних величин, шансы отклонения падают все быстрее и быстрее (экспоненциально). Если вам нужна сжатая формулировка, вот она: резкий рост скорости падения шансов при удалении от центра, то есть от среднего. Чтобы это проиллюстрировать, я беру пример гауссовой величины, такой как рост, и немного упрощаю его, чтобы сделать более наглядным. Предположим, что средний рост (мужчин и женщин) 1 метр 67 сантиметров, или 5 футов 7 дюймов. Будем считать, что так называемая единица отклонения равна в данном случае го сантиметрам. Взглянем на ряд прибавок к 1 метру 67 сантиметрам и рассмотрим шансы того, что кто-то окажется столь высоким.
на 10 см выше среднего (т. е. выше 1 м 77 см, или 5 футов 10 дюймов): 1 из 6,3на 20 см выше среднего (т. е. выше 1 м 87 см, или б футов 2 дюймов): 1 из 44на 30 см выше среднего (т. е. выше 1 м 97 см, или б футов б дюймов): 1 из 740на 40 см выше среднего (т. е. выше 2 м 07 см, или б футов 9 дюймов): 1 из 32 000на 50 см выше среднего (т. е. выше 2 м 17 см, или 7 футов 1 дюйма): 1 из 3 500 000на 60 см выше среднего (т. е. выше 2 м 27 см, или 7 футов 5 дюймов): 1 из 1 000 000 000на 70 см выше среднего (т. е. выше 2 м 37 см, или 7 футов 9 дюймов): 1 из 780 000 000 000на 80 см выше среднего (т.е. выше 2 м 47 см, или 8 футов 1 дюйма): 1 из 1 600 000 000 000 000на 90 см выше среднего (т. е. выше 2 м 57 см, или 8 футов 5 дюймов): 1 из 8 900 000 000 000 000 000на 100 см выше среднего (т. е. выше 2 м 67 см, или 8 футов 9 дюймов): 1 из 130 000 000 000 000 000 000 000...ина 110 см выше среднего (т.е. выше 2 м 77 см, или 9 футов 1 дюйма): 1 из 36 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000.
Думаю, не ошибусь, если скажу, что после 22 отклонений, означающих превышение среднего роста на 2 м 20 см, шансы достигают числа, имеющего в знаменателе так называемый "гугол" — единицу со ста нулями.
Цель этого списка — проиллюстрировать ускорение. Обратите внимание на разницу в шансах между* превышением среднего роста на 60 и на 70 сантиметров: всего 4 лишних дюйма снижают шансы с одного на миллиард до одного на 780 миллиардов! А теперь посмотрите на скачок между 70 и 80 сантиметрами: еще 4 дюйма, и шансы слетают с одного на 780 миллиардов до одного на 1,6 миллиона миллиардов!
Это стремительное убывание вероятности какого-либо явления и приводит к игнорированию аномалий. Только одна кривая может давать такое убывание — гауссиана (и ее не-масштабируемые родичи).
Принцип Мандельброта
Для сравнения возьмем другой пример: взглянем на шансы быть состоятельным в Европе. Будем исходить из того, что состоятельность там — величина масштабируемая, то есть мандельбротовская. (Это конечно же приблизительное описание; оно упрощено, чтобы подчеркнуть логику масштабируемого распределения.)
Масштабируемое распределение капиталаЛюди с чистым капиталом выше 1 миллиона евро: 1 из 62,5выше 2 миллионов евро: 1 из 250выше 4 миллионов евро: 1 из 10ООвыше 8 миллионов евро: 1 из 4000выше 16 миллионов евро: 1 из 16 ОООвыше 32 миллионов евро: 1 из 64 ОООвыше 320 миллионов евро: 1 из 6 400 000
Скорость убывания здесь остается постоянной (падения нет!). Удваивая сумму денег, урезаем долю в четыре раза, не важно, на каком уровне, — 8 миллионов евро или 16 миллионов евро. Вот вам, по существу, и разница между Среднестаном и Крайнестаном.
Напомню сравнение между масштабируемым и немасштабируемым, проведенное нами в главе 3. Масштабируемость означает, что нет встречного ветра, который мешает двигаться вперед.
Конечно, мандельбротовский Крайнестан может принимать разные формы. Рассмотрим капитал в предельно концентрированной версии Крайнестана; там, удваивая капитал, уполовиниваешь долю. Результат количественно отличается от примера, приведенного выше, но он подчиняется той же логике.
Фрактальное распределение капитала с большой дифференциациейЛюди с чистым капиталом выше 1 миллиона евро: 1 из 63выше 2 миллионов евро: 1 из 125выше 4 миллионов евро: 1 из 250выше 8 миллионов евро: 1 из 500выше 16 миллионов евро: 1 из 1000выше 32 миллионов евро: 1 из 2000выше 320 миллионов евро: 1 из 20 000выше 640 миллионов евро: 1 из 40 000
Если бы мы подсчитывали капиталы по методу Гаусса, то наблюдали бы следующую картину.
Распределение капитала, исходя из закона ГауссаЛюди с чистым капиталом выше 1 миллиона евро: 1 из 63выше 2 миллионов евро: 1 из 127 ОООвыше 3 миллионов евро: 1 из 14 ООО ООО ОООвыше 4 миллионов евро: 1 из 886 ООО ООО ООО ООО ОООвыше 8 миллионов евро: 1 из 16 ООО ООО ООО ООО ООО ООО ООО ООО ООО ООО ООО выше 16 миллионов евро: 1 из... ни один из моих компьютеров не справляется с вычислением.
Этими списками я хочу показать качественное различие парадигм.
Итак, вторая парадигма масштабируема; в ней нет встречного ветра, который сбивает с ног. Заметим, что существует другой термин для определения масштабируемости — степенные законы.
Само по себе осознание, что мы живем в среде, где властвуют такие законы, дает нам немного. Почему? Потому что в реальной жизни придется производить вычисления куда более сложные, чем те, что предлагаются Гауссом. Только "гауссова кривая" довольно легко открывает свои свойства. Мой метод—это скорее определенный взгляд на мир в целом, а не какое-то точное решение.
что надо запомнить
Запомните: любая разновидность "гауссовой кривой" сопротивляется силе встречного ветра, под порывами которого шансы падают все быстрее и быстрее по мере удаления от нормы, в то время как масштабируемые, или мандельбротовские, варианты никаким ветрам не подвластны. Это в общем-то главное из того, что вам необходимо знать.
Неравенство
Давайте приглядимся получше к природе неравенства. В гауссовой структуре по мере увеличения отклонений неравенство все больше сходит на нет — из-за роста скорости падения. С масштабируемым все иначе: неравенство постоянно остается тем же. Неравенство среди сверхбогатых такое же, как и среди просто богатых, — оно не стирается.
Рассмотрим конкретный пример. Возьмем наугад, скажем, двух американцев, которые вместе зарабатывают 1 миллион долларов в год. Каково самое вероятное распределение этих денег? В Среднестане — по полмиллиона каждому. В Крайнестане расклад был бы таков: $50 000 и $950 000.
В ситуации с продажами книг расклад получился бы еще более асимметричным. Если бы два автора продали миллион книг, то выяснилось бы, что раскуплено 993 000 экземпляров книги одного, а другого — 7000. Эта комбинация куда вероятнее, чем то, что каждой книги продалось по 560 000 экземпляров. Чем крупнее сумма, тем асимметричней будут части, на которые она разобьется.
Почему именно так? Для сравнения возьмем, например, человеческий рост. Если бы я сказал вам, что суммарный рост двух человек 14 футов, вы, скорее всего, разбили бы это число пополам: по 7 футов у каждого, но не стали бы предполагать, что у одного рост 2 фута, у другого 12 футов. Даже вариант 8 футов и 6 футов маловероятен! Люди выше 8 футов настолько редки, что такая комбинация была бы невозможна.
Крайнестан и правило 80/20
Вы когда-нибудь слышали о правиле 80/20? Это своего рода "брэнд" степенного закона — собственно, с этого и началось, когда Вильфредо Парето заметил, что 80 процентов земли в Италии принадлежит 20 процентам населения. Некоторые трактуют это правило таким образом: 80 процентов работы делается 20 процентами населения. Или еще вариант: 80 процентов усилий дают только 20 процентов результата, и наоборот.
Замечу, что правило это сформулировано не самым впечатляющим образом: его легко было бы назвать правилом 50/01, то есть 50 процентов работы делается 1 процентом работников. В последней формулировке мир предстает еще более несправедливым, но она абсолютно идентична первой. В каком смысле? Ну если уж неравенство существует, то нужно уточнить: те, кто составляют 20 процентов в правиле 80/20, вносят разный по объему вклад — лишь немногие из них обеспечивают ту самую, львиную, долю результатов.
Примерно один из сотни обеспечивает чуть больше половины общего вклада.
Правило 80/20 — только метафора; это не общее правило, тем более — не строгий закон. В американском книжном бизнесе пропорция скорее будет 97/20 (то есть 97 процентов продаж книг приходятся на долю 20 процентов авторов); если проанализировать соотношение в литературе не художественной, разрыв будет еще более разительным (половину продаж обеспечивают 20 книг из почти 8 тысяч).
Хочу заметить, что не все тут так уж неопределимо. В некоторых ситуациях концентрация 80/20 обладает весьма предсказуемыми и опознаваемыми свойствами, что позволяет принимать уверенные решения, поскольку вы можете заранее вычленить эти важные 20 процентов. Такие ситуации очень легко контролировать. Например, Малкольм Гладуэлл писал в "Нью-Йоркере", что лишь немногие зверюги охранники издеваются над заключенными. Отфильтруйте этих охранников, и уровень издевательств в тюрьме резко упадет. С другой стороны, в издательском деле никогда заранее не знаешь, какая книга принесет жирную прибыль. То же и с войнами: предугадать, какой именно очередной конфликт погубит огромную часть населения планеты, невозможно.
Трава и деревья
Начну эту главу с того, что подытожу и повторю рассуждения, уже изложенные ранее. Шкалирование неопределенности, основанное на кривой нормального распределения, не учитывает возможности (и соответственно влияния) резких скачков или разрывов, а потому неприменимо в Крайнестане. Пользоваться им — все равно что рассматривать траву, вглядываясь в мелкие стебельки и не замечая (огромных!) деревьев. Непредсказуемые большие отклонения, конечно, редки, но на них нельзя закрывать глаза, поскольку их кумулятивный эффект огромен.
Традиционное гауссово исследование мира начинается с фокусирования на обычном, и лишь потом, как нечто побочное, рассматриваются исключения или так называемые "выбросы". Но есть и другой подход, который за основу берет исключительное, а второстепенным считает обычное.
Я не раз уже подчеркивал, что есть случайности двух видов, качественно различные, как воздух и вода. Одна не зависит от крайностей; другая, наоборот, находится под их сильным воздействием. Одна не порождает Черных лебедей; другая порождает. Недопустимо использовать для газа те же характеристики, что и для жидкости. И если бы это было допустимо, такой подход не назывался бы "приближением". Газ не "приближается" к жидкости.
Можно с толком использовать гауссов метод для упорядочения тех величин, которые по объективным причинам не слишком сильно удаляются от средних значений. Если переменные находятся в зоне действия закона гравитации или имеются физические ограничения, препятствующие чрезмерной дифференциации размеров, значит, мы попали в Среднестан. Если сила равновесия настолько велика, что малейшая разбалансировка мгновенно ликвидируется, то опять-таки гауссов метод вполне приемлем. В противном случае грош ему цена. Вот почему экономика в общем-то зиждется на понятии равновесия: оно помимо всего прочего устраивает экономистов тем, что позволяет втискивать экономические явления в гауссовы рамки.
Заметьте, я не утверждаю, что среднестанский тип случайности не допускает никаких крайностей. Но они настолько редки, что в конечном итоге роль их очень невелика. Эффект таких крайностей ничтожно мал и уменьшается с увеличением общей совокупности.
Теперь немного конкретики: если у вас имеется набор великанов и карликов, а иначе говоря, наблюдения, различающиеся на несколько порядков величины, вы можете все-таки оставаться на территории Среднестана. Почему? Сейчас выясним. Предположим, что у вас есть выборка в тысячу человек, с широким диапазоном от карлика до великана. Скорее всего, в этой выборке встретится много великанов, а не только какой-то один, случайный. Неожиданно возникший лишний великан не изменит среднего показателя, потому что заранее предполагается, что великанов несколько и ваш средний показатель, скорее всего, и так достаточно высок. Другими словами, наибольший экземпляр не может сильно возвышаться над средним. Средний показатель всегда учитывает наличие как великанов, так и карликов, поэтому никто из них не попадет в разряд редкостных исключений — если только не народится вдруг какой-нибудь уникальный мегавеликан или микрокарлик. Это будет Среднестан с большой амплитудой разброса.
Снова отметим следующую закономерность: чем реже событие, тем менее точно мы можем оценить степень его вероятности — даже в рамках гауссианы.
Позвольте вам продемонстрировать, как "гауссова кривая" вытесняет из жизни случайность — потому она так и популярна. Мы любим ее за то, что она дает определенность! Каким образом? За счет усреднения, о чем сейчас и пойдет разговор.
Почему нам удается спокойно пить кофе
Вспомним кое-что из обсуждения Среднестана в главе 3: ни одно отдельное наблюдение не влияет на итог. И это свойство будет приобретать все большую и большую значимость по мере увеличения рассматриваемой вами совокупности. Средние показатели будут все больше и больше стабилизироваться, пока в конце концов самые разные выборки не станут похожими как две капли воды.
За свою жизнь я выпил множество чашек кофе (это моя главная слабость). Но никогда не видел, чтобы чашка подпрыгнула на два фута и кофе не проливался на эту рукопись без внешнего вмешательства (даже в России). В самом деле, чтобы стать свидетелем такого события, недостаточно невинного пристрастия к кофе; потребуется больше жизней, чем, пожалуй, можно вообразить, — шансы равны единице после такого количества нолей, что я не смогу их выписать, даже если употреблю на это все свое свободное время.
Но законы физики свидетельствуют, что чашка все же могла бы подпрыгнуть, — это очень маловероятно, но возможно. Частицы постоянно куда-нибудь прыгают. Как получилось, что кофейная чашка, сама состоящая из прыгающих частиц, не прыгает? Причина, говоря попросту, вот в чем: чтобы чашка подпрыгнула, нужно, чтобы все частицы прыгнули в одну и ту же сторону и сделали бы это вместе несколько раз подряд (при компенсирующем движении стола в обратную сторону). Все несколько триллионов частиц в моей кофейной чашке не прыгнут в одну и ту же сторону; этого не случится, сколько бы ни просуществовала еще наша Вселенная. Поэтому я могу спокойно поставить кофейную чашку на край письменного стола и призадуматься о более серьезных зонах неопределенности.
Спокойствие, гарантированное моей кофейной чашке, иллюстрирует то, как гауссова случайность "укрощается" усреднением. Если бы моя чашка была одной большой частицей и вела себя так, как обычно ведет себя отдельная частица, то ее прыжки доставляли бы массу неприятностей. Но моя чашка — это триллионы очень маленьких частиц.
Хозяева казино прекрасно это понимают, и поэтому они никогда (если всё правильно делают) не теряют денег. Они просто не позволяют одному игроку сделать крупную ставку, вместо этого предпочитая, чтобы множество игроков сделали ряд ставок ограниченного размера. Игроки могут в сумме поставить 20 миллионов долларов, но не надо беспокоиться о благополучии казино: ставки равны в среднем 20 долларам; казино ограничивает ставки тем максимумом, который позволяет хозяевам казино спокойно спать по ночам. Поэтому колебания доходов казино будут смехотворно малы, независимо от активности всех имеющихся в наличии игроков. Никто из них никогда не выйдет из казино с миллиардом долларов.
Вышеизложенное представляет собой проявление высшего закона Среднестана: когда игроков множество, отдельный игрок практически не повлияет на итог, кроме как по мелочи.
Отсюда следует то, что колебания вокруг среднего в гауссиане, также называемые "ошибками", на самом деле — не повод для волнений. Они маленькие, их можно легко отбросить. Они — одомашненные флуктуации вокруг среднего.
Любовь к определенности
Если когда-то в колледже вам довелось прослушать (скучнейший) курс лекций по статистике и вы не поняли почти ничего из того, чем так восторгался профессор, если вы так и не уяснили, что такое стандартное отклонение, не расстраивайтесь. Понятие стандартного отклонения бессмысленно вне Среднестана. Ясно, что гораздо полезней и куда приятней было бы прослушать курс по биологическим аспектам эстетики или постколониальному африканскому танцу, и это проверяется эмпирически.
Стандартные отклонения не существуют вне гауссианы, а если и существуют, то они не важны и мало что объясняют. Но дальше — хуже. Гауссово семейство (которое включает различных друзей и родственников, скажем, закон Пуассона) — единственный класс распределений, для описания которого достаточно стандартного отклонения (и среднего показателя). Больше ничего не нужно. "Гауссова кривая" — находка для любителей упрощений.
Есть другие понятия, которые почти ничего не значат вне гауссовой ситуации — корреляция и, хуже того, регрессия. Но они глубоко внедрились в наши методы; в любом деловом разговоре непременно услышишь слово корреляция.
Чтобы увидеть, сколь бессмысленна бывает корреляция вне Среднестана, рассмотрим данные прошлых лет, по две величины, которые уж наверняка из Крайнестана, скажем, рынки облигаций и акций, или две цены акций, или такие две величины, как изменения в продажах детских книг в США и в производстве удобрений в Китае; или цены на недвижимость в Нью-Йорке и обороты монгольского фондового рынка. Измерьте корреляцию между парами величин за различные периоды, скажем, за годы 1994, 1995, 1996 и т. д. Корреляционное соотношение, скорее всего, будет резко меняться от периода к периоду. И при этом все говорят о корреляции как о некой реальности, делая ее осязаемой, наделяя ее физическими свойствами, материализуя ее.
Мы склонны конкретизировать и то, что называем "стандартными" отклонениями. Рассмотрим любой ряд прошлых цен или значений. Разбейте его на отрезки и измерьте их "стандартное" отклонение. Удивлены? Каждая выборка даст свое "стандартное" отклонение. Тогда почему все говорят о стандартных отклонениях? Попробуй пойми.
Картина тут та же, что и при искажении нарратива: когда сравниваешь прошлые факты и вычисляешь одну-единствен-ную корреляцию или стандартное отклонение, такой нестабильности не замечаешь.
Как вызывать катастрофы
Если вы пользуетесь термином статистически значимый, опасайтесь иллюзии определенности. Всегда есть вероятность, что кто-то примет свои ошибки наблюдения за гауссовы, но тогда и контекст должен быть соответствующим, гауссовым, то есть среднестанским.
Чтобы показать, сколь неизбывно злоупотребление гауссианой и сколь это может быть опасно, рассмотрим (скучную) книгу под названием "Катастрофа", написанную судьей Ричардом Познером, плодовитым писателем. Познер сетует, что госчиновники ничего не смыслят в случайности, и рекомендует высшим должностным лицам учиться статистике... у экономистов. Поистине судья Познер пытается провоцировать катастрофы. Жаль, конечно, что он большую часть времени отдает писательству, а не чтению, но, несмотря на это, мыслитель он проницательный, глубокий и оригинальный. Просто, как и многие другие, не знает о том, что между Среднестаном и Крайнестаном есть существенные различия, и свято верит, что статистика — "наука", а не обман. Если столкнетесь с ним, расскажите ему, как все обстоит на самом деле.
УСРЕДНЕННОЕ ЧУДОВИЩЕ КЕТЛЕ
Эта химера, называемая "гауссовой кривой", или гауссианой, создана была не Гауссом. Да, он работал над ней, но как математик-теоретик, не прилагая ее к устройству нашей реальности, как это делают ученые со статистическим поворотом ума.
Г. X. Харди писал в "Апологии математика":
"Настоящая" математика "настоящих" математиков, таких как Ферма, Эйлер, Гаусс, Абель и Риман, почти целиком "бесполезна" (что верно не только для "чистой", но и для "прикладной" математики)".
Ранее я уже говорил, что кривая нормального распределения была в общем-то изобретением игрока, Абрахама де Муавра (1667-1754), французского изгнанника-кальвиниста, который провел большую часть своей жизни в Лондоне, хотя и говорил по-английски с сильным акцентом. Но, как мы сейчас с вами увидим, одним из самых злостных вредителей в истории развития мысли надо считать совсем даже не Гаусса, а Кетле.
Адольф Кетле (1796-1874) создал понятие "Phomme moyen" — "физически средний человек". Сам Кетле, "человек, наделенный мощными творческими страстями, творец, полный энергии", ни в чем не был moyen. Он писал стихи и даже принял участие в сочинении оперы. Беда заключалась в том, что Кетле был математиком, а не ученым-эмпириком, только сам этого не осознавал. Он усмотрел гармонию в кривой нормального распределения.
У этой проблемы два уровня.
Primo. Кетле увлекся идеей "нормативности", он хотел подогнать мир под некие средние стандарты, питая иллюзию, что это среднее и есть "норма". Конечно, было бы замечательно, если бы мы могли игнорировать влияние на нашу действительность всего необычного, "ненормального", то есть Черного лебедя. Но оставим эту мечту утопистам.
Secondo вытекает из primo и представляет собой серьезную эмпирическую проблему. Математику повсюду мерещились колоколовидные кривые. Они ослепляли его, и я вновь убедился: если к тебе в голову забралась такая кривая, ее трудно вытравить оттуда. Позже Фрэнк Исидро Эджуорт будет называть кетлизмом эту опасную тенденцию подводить все под "колокол".
Золотая посредственность
Концепция Кетле пришлась весьма кстати идеологам того времени, которые как раз жаждали чего-либо подобного. Вы только взгляните на список его современников: Сен-Симон (1760-1825), Пьер-Жозеф Прудон (1809-1865), Карл Маркс (1818-1883), каждый — создатель своей версии социализма. В эпоху, последовавшую за веком Просвещения, все искали aurea mediocritas, золотую середину: в богатстве, росте, весе и т. д. Это стремление подчас заставляет принимать желаемое за действительное, оно во многом навеяно поисками гармонии и... платонизмом.
Я навсегда запомнил директиву своего отца — "in medio stat virtus", "доблесть — в умеренности". Да, долгое время это было идеалом; посредственность в этом смысле даже считалась золотой. Всеохватывающая посредственность.
Но Кетле поднял эту идею на новый уровень. На основе собранных им данных он начал создавать среднестатистические стандарты. Обхват груди, рост, вес детей при рождении — мало что избежало стандартизации. Отклонения от нормы, как он заметил, становятся экспоненциально более редкими с увеличением амплитуды отклонения. Покончив с физическими характеристиками, месье Кетле переключился на социальную сферу. L'homme moyen имел свои привычки, свои запросы, свои методы.
Сконструировав таким образом l'homme moyen physique и l'homme moyen moral (физического среднего человека и нравственного среднего человека), Кетле обозначил некие пределы отклонения от среднего, внутри которых любого человека помещают слева или справа от центра и, по сути, "бракуют" тех, кто оказывается у самого края. Их объявляют аномалией. Это, естественно, очень вдохновило Маркса, который ссылается на понятие среднего, или нормального, идивидуума, введенное Кетле. Он утверждает в "Капитале", что общественные различия (например, те, что обусловлены распределением капитала) должны быть сведены к минимуму.
Надо отдать должное научной элите времен Кетле. Коллеги настороженно отнеслись к его теории. Начнем с того, что Огюстен Курно, философ, математик, экономист, усомнился в том, что можно учредить некий стандарт человека только на основании количественных характеристик. Этот стандарт будет зависеть от рассматриваемой выборки. Замеры, произведенные в одной провинции, могут отличаться от замеров в другой провинции. Ну и какие из них должны быть эталоном? По мнению Курно, Thomme moyen был бы чудовищем.
Я так поясню его мысль.
Даже если кому-то вдруг очень захотелось бы стать средним человеком, то ему пришлось бы утаить от "замерщиков" свои профессиональные таланты, то, в чем он неизбежно превосходит остальных, — человек не может быть средним во всем. Пианист будет лучше "среднего" играть на пианино, но хуже, чем предписано "нормой", ездить верхом. Чертежник будет лучше чертить и так далее. Понятие человека, считающегося средним, отличается от понятия человека, среднего во всем, что он делает. В действительности абсолютно средний человек был бы наполовину мужчиной, наполовину женщиной. Кетле совершенно упустил это из виду.
Ошибка Бога
Еще больше удручает то, что во времена Кетле гауссово распределение называлось "la loi des erreurs" — "закон погрешностей", так как одним из самых ранних его приложений было распределение погрешностей в астрономических расчетах. Вам тоже не по себе? С отклонением от среднего (в данном случае и от медианы тоже) обращались как с погрешностью! Не удивительно, что Марксу понравились идеи Кетле.
Понятие усредненности распространилось мгновенно. "Так положено" спутали с "есть" — и все это с благословения науки. Понятие середняка глубоко вошло в культуру, ожидавшую нарождения европейского среднего класса, в молодую культуру постнаполеоновского лавочника, опасающегося излишнего богатства и интеллектуального блеска. В принципе считается, что мечта об обществе с нивелированными доходами отвечает стремлениям всякого рационально мыслящего человека, вынужденного иметь дело с генетической лотереей. Если бы вам предложили выбрать общество, в котором вы родитесь в следующей жизни, но неизвестно кем именно, скорее всего вы не стали бы рисковать — предпочли бы такое общество, в котором нет существенной разницы в доходах.
Курьезной кульминацией восхваления посредственности стало появление во Франции так называемого "пужадизма", политического движения, начавшегося с выступлений лавочников. Это было горячее братство людей более или менее благополучных, надеявшихся, что вся остальная вселенная подстроится под них — своего рода случай непролетарской революции. Их мелкоторгашеский менталитет проявлялся даже в том, как они обращались с математикой. Думал ли Гаусс, что создает формулы для лавочников?
Пуанкаре приходит на помощь
Сам Пуанкаре относился к гауссиане с большой опаской. Я подозреваю, что он внутренне съеживался, когда ему предлагали этот и подобные подходы к моделированию неопределенности. Достаточно вспомнить, что кол околовидная кривая изначально предназначалась для измерения астрономических погрешностей, а уже небесная механика самого Пуанкаре проникнута куда более глубоким пониманием неопределенности.
Пуанкаре писал, что один из его друзей, "выдающийся физик", жаловался ему, что физики пользуются "гауссовой кривой", потому что, вслед за математиками, считают ее математической необходимостью, математики же пользуются ею, потому что считают ее эмпирической данностью.
Будем справедливы
Хочу особо отметить, что вообще-то (если оставить в стороне издержки в виде психологии лавочников) я искренне верю в ценность срединности и посредственности — какой гуманист не мечтает уменьшить неравенство между людьми? Нет ничего более отталкивающего, чем безрассудно сотворенный идеал сверхчеловека! На самом деле меня тревожит иная проблема — эпистемологическая, то есть проблема познания. Пора уяснить, что реальность — не Среднестан и нам надо научиться с этим жить.
"Греки бы его обожествили"
Список людей, у которых в мозгу угнездилась (благодаря своей платонической чистоте) гауссиана, невероятно велик.
Сэр Фрэнсис Гальтон, двоюродный брат Чарльза Дарвина и внук Эразма Дарвина, был наряду со своим кузеном одним из последних независимых ученых-джентльменов, к каковым также принадлежали лорд Кавендиш, лорд Кельвин, Людвиг Витгенштейн (на свой лад) и отчасти наш суперфилософ Бертран Рассел. Хотя Джон Мэйнард Кейнс не вполне вписывался в эту категорию, он мыслил в унисон с ней. Гальтон жил в викторианскую эпоху, когда обладатели наследственного состояния и неограниченного досуга не только упражнялись в верховой езде и стрельбе по дичи, но становились философами, учеными или (менее одаренные) политиками. Как это ни печально, вместе с той эпохой ушло нечто невосполнимое: истинные подвижники, занимающиеся наукой ради науки, не думающие о карьере.
К сожалению, занятия наукой из бескорыстной любви к знанию не гарантируют, что ты будешь двигаться в правильном направлении. Познакомившись с "нормальным" распределением, Гальтон влюбился в него. Говорят, он однажды воскликнул, что, если бы грекам было о нем известно, они бы обожествили его. Возможно, восторг Гальтона тоже поспособствовал воцарению гауссианы в научных умах.
Гальтон не сподобился обзавестись надлежащим математическим багажом, но был прямо-таки одержим измерениями. Он не знал о законе больших чисел, но сам открыл его, проанализировав собранные данные. Он сконструировал доску Гальтона, или "quincunx", — что-то вроде автомата для игры в пинбол, с помощью которого можно смоделировать колоколовидную кривую, — об этом я расскажу через несколько абзацев. Правда, Гальтон применял кривую нормального распределения в таких областях, как генетика и наследственность, где ее использование оправданно. Но его энтузиазм помог внедрить зарождавшиеся статистические методы в социальные сферы.
Ответьте, пожалуйста, "да" или "нет"
А сейчас позвольте мне поговорить о размерах ущерба.
Если вам нужны качественные (а не количественные) выводы, как в психологии или медицине, где вы вполне обойдетесь "безразмерными" ответами "да" или "нет", то можете спокойно допустить, что находитесь в Среднестане. Влияние невероятного не будет слишком большим. У него есть рак либо нет; она беременна либо нет и так далее. Смертельность или беременность не имеют степеней (если не рассматривать их в эпидемических масштабах). Но, когда вы манипулируете совокупностями, различными по величине (такими как доход, ваш капитал, прибыль с портфеля ценных бумаг или продажи книг), гауссиана может вас здорово подвести, так как эта сфера не в ее компетенции. Одно-единственное число способно порушить все ваши средние показатели; одна-единственная потеря — зачеркнуть сотни и сотни прибылей. Уже нельзя говорить: "Это исключение". Заявление "да, я могу потерять деньги" довольно бессмысленно, если не указать хотя бы приблизительную сумму. Потерять весь свой капитал или потерять долю своего дневного дохода — все-таки разница.
Именно поэтому эмпирическая психология и открытые ею свойства человеческой природы, о которых я говорил в начале этой книги, не страдают от ложного использования гауссианы; психологам вообще повезло, ибо переменные, которыми они оперируют, в большинстве своем не выходят за рамки обычной гауссовой статистики. Выясняя, сколько человек в выборке имеют определенную особенность или склонность к ошибке, они обычно добиваются результата посредством ответов "да" или "нет". Ни одно отдельно взятое наблюдение не может в корне изменить общего заключения.
Теперь я представлю вам идею гауссианы, разобрав ее по кирпичикам.
МЫСЛЕННЫЙ (ЧИСЛЕННЫЙ) ЭКСПЕРИМЕНТ, ДЕМОНСТРИРУЮЩИЙ, ОТКУДА ПРОИСХОДИТ КРИВАЯ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
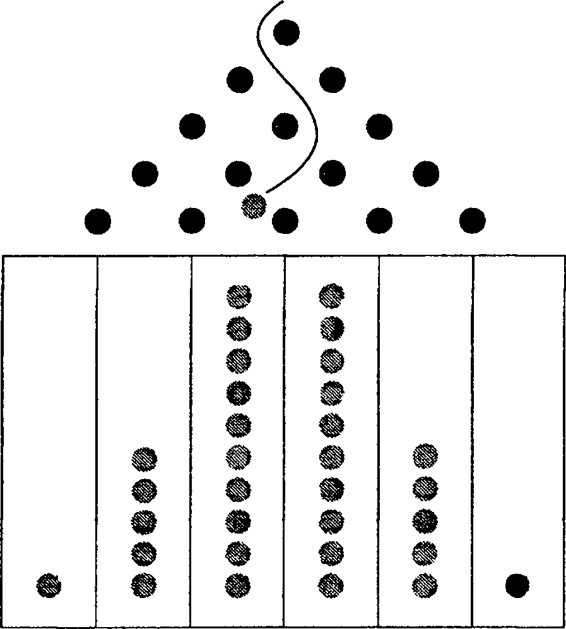
Рассмотрим своего рода пинбольный автомат, такой, как на рисунке 8. Запустим 32 шара, предполагая, что доска правильно сбалансирована, так что у шара одинаковые шансы свалиться направо и налево на любом пересечении, наткнувшись на штырь. Ожидаемый результат — большая часть шаров "приземлится" в центральных ячейках: чем ячейки дальше от центра, тем меньше туда попадет шаров.
Затем проведем мысленный эксперимент. Человек бросает монетку, смотрит, что выпало, орел или решка, и в зависимости от этого делает шаг влево или вправо. Это так называемое "случайное блуждание" не обязательно связано с ходьбой. С таким же успехом можно представить, что вместо шага вправо или влево вы каждый раз выигрываете или проигрываете доллар, при этом ведя учет долларам, накопившимся у вас в кармане.
Предположим, я заключаю с вами честное пари, где возможность выигрыша у вас примерно та же, что и проигрыша. Кидаем монетку. Орел — вы получаете доллар, решка — теряете доллар.
При первом броске вы либо выиграете, либо проиграете.
При втором броске число возможных исходов удваивается. Вариант 1: выигрыш-выигрыш. Вариант 2: выигрыш-проигрыш. Вариант 3: проигрыш-выигрыш. Вариант 4: проигрыш-проигрыш. У каждого из этих вариантов одинаковые шансы, комбинация из одного выигрыша и одного проигрыша встречается вдвое чаще, так как варианты 2 и 3, выигрыш-проигрыш и проигрыш-выигрыш, приводят к одинаковому результату. И в этом ключ к гауссиане. В середине очень многое сглаживается, и, как мы увидим, к середине тяготеет большинство. Поэтому если при каждом броске разыгрывается доллар, то на втором броске ваши шансы таковы: 25 процентов, что вы приобретете или потеряете 2 доллара, и 50 процентов, что выйдете в нуль.
Третий бросок снова удваивает число исходов, так что их становится восемь. Вариант 1 (выигрыш-выигрыш после двух бросков) разветвляется на выигрыш-выигрыш-выигрыш и выигрыш-выигрыш-проигрыш. Мы добавляем выигрыш или проигрыш к каждому из предыдущих результатов. Вариант 2 разветвляется на выигрыш-проигрыш-выигрыш и выигрыш-проигрыш-проигрыш. Вариант з разветвляется на проигрыш- выигрыш-выигрыш и проигрыш-выигрыш-проигрыш. Вариант 4 разветвляется на проигрыш-проигрыш-выигрыш и проигрыш-проигрыш-проигрыш.
Теперь у нас восемь вариантов, все одинаково вероятные. Заметим, что снова можно сгруппировать средние исходы, в которых выигрыш перечеркивает проигрыш. (На доске Гальтона ситуации, когда шар отлетает влево, а затем вправо, или наоборот, преобладают, так что в результате в середине оказывается много шаров.)
Совокупный итог таков: 1) три выигрыша; 2) два выигрыша, один проигрыш, итого один выигрыш; з) два выигрыша, один проигрыш, итого один выигрыш; 4) один выигрыш, два проигрыша, итого один проигрыш; 5) два выигрыша, один проигрыш, итого один выигрыш; 6) два проигрыша, один выигрыш, итого один проигрыш; 7) два проигрыша, один выигрыш, итого один проигрыш; и, наконец, 8) три проигрыша.
Из восьми вариантов вариант трех выигрышей встречается однажды. Вариант трех проигрышей встречается однажды. Вариант одного итогового проигрыша (один выигрыш, два проигрыша) встречается три раза. Вариант одного итогового выигрыша (один проигрыш, два выигрыша) встречается три раза.
Сделаем еще один бросок, четвертый. Будет шестнадцать равновероятных исходов. Один вариант четырех выигрышей, один вариант четырех проигрышей, четыре варианта двух выигрышей, четыре варианта двух проигрышей и шесть вариантов выхода в нуль.
"Quincunx" (это латинское производное от числительного "пять") в нашем пинбольном примере представляет собой иллюстрацию пятого броска или шага, после которого шансы, как легко высчитать, возрастают до шестидесяти четырех. Вот идея, воплощенная в доске Фрэнсиса Гальтона. Гальтону явно недоставало здоровой лени и математической сметки: вместо того чтобы сооружать такое устройство, вообще-то проще было поработать с алгеброй или провести мысленный эксперимент вроде нашего.
Однако продолжим игру до сорокового броска. На это уйдет лишь несколько минут, но понадобится калькулятор, чтобы вычислить количество исходов, так как наши мозги с этим не справятся. Получится 1 099 511 627 776 возможных комбинаций — то есть более тысячи миллиардов. Не затрудняйтесь просчитывать шаг за шагом — это будет два в сороковой степени, так как на каждом этапе каждая цепочка раздваивается. (Вспомните, как мы добавили выигрыш и проигрыш к вариантам третьего броска, удвоив число вариантов.) Из этих комбинаций только одна будет состоять из сорока выигрышей и только одна — из сорока проигрышей. Остальные будут тяготеть к середине, в данном случае — к нулю.
Вам уже ясно, что этот тип случайности чрезвычайно беден крайностями. Все сорок бросков оказываются выигрышными лишь в одном случае из 1 099 511 627 776. Если вы станете час за часом проделывать это упражнение с сорока бросками, вам придется здорово попотеть, прежде чем выпадут сорок орлов (или сорок решек) подряд. Поскольку вы наверняка будете прерываться, чтобы поесть, поспорить с друзьями и соседями, попить пива и поспать, то готовьтесь, ради такой удачи, прожить около четырех миллионов жизней. А представьте, что вы добавляете один лишний бросок. Чтобы выкинуть орла сорок один раз подряд, понадобится потратить на попытки восемь миллионов жизней! Переход от 40 к 41 уменьшает шансы вдвое. Это — ключевое свойство немасштабируемого подхода к анализу случайности: крайние отклонения убывают с все возрастающей скоростью. А пятьдесят орлов подряд могут выпасть один-единственный раз на протяжении 4 миллиардов жизней!
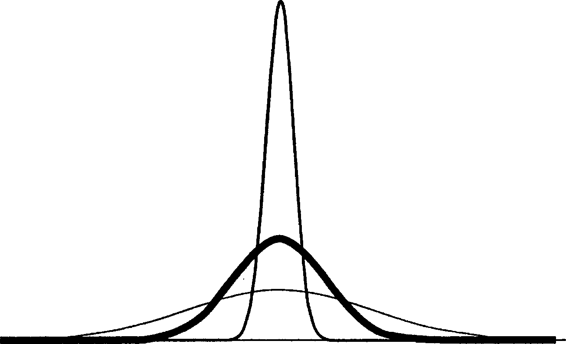
Мы еще не получили "гауссову кривую", но сильно приблизились к ней. Пока это протогауссиана, но суть уже видна. (На самом деле вы никогда не встретите "гауссову кривую" в чистом виде, так как это платоническая фигура — к ней можно только стремиться, но достичь ее невозможно.) Но, как показывает рисунок 9, знакомая колоколовидная форма уже просматривается.
Способны ли мы ближе подойти к совершенной "гауссовой кривой"? Да. Для этого нужно разбить раунд на большее количество менее результативных бросков. Можно ставить на кон не доллар, а десять пенсов и бросать не 40, а 4000 раз, складывая результаты. Ожидаемый риск будет приблизительно тем же — ив этом фокус. В соотношении двух названных вариантов игры есть небольшой сознательный сдвиг. Мы умножили число бросков на 100, но поделили размер ставки на 10 — не ищите сейчас причины, просто предположите, что варианты "эквивалентны". Общий риск эквивалентен, но теперь нам открылась возможность выиграть или проиграть 40 долларов за 400 последовательных бросков.

Шансы равны единице на единицу со 120 нулями,то есть 1/1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000.
Продолжим процесс дробления. Будем бросать 400 000 раз, ставя на кон по 1 центу и подходя, таким образом, все ближе и ближе к гауссиане. Рисунок показывает распределение результатов между 40 и минус 40 долларами, то есть восьмьюдесятью смысловыми точками. При ставке в 1 цент мы доводим их до 8000 смысловых точек.
Пойдем дальше. Мы можем бросить монету 4000 раз, ставя по 1/10 цента. Ну а как насчет 400 000 раз по 1/1000 цента? Совершенная кривая Гаусса (как платоническая форма) — это отображение бесконечного числа бросков с бесконечно малыми ставками. Не пробуйте их себе представить — не получится. Нам нет смысла говорить о "бесконечно малых" ставках (поскольку у нас их бесконечное множество, а значит, мы имеем дело с тем, что математики называют бесконечной структурой). Но хочу вас обрадовать: существует альтернатива.
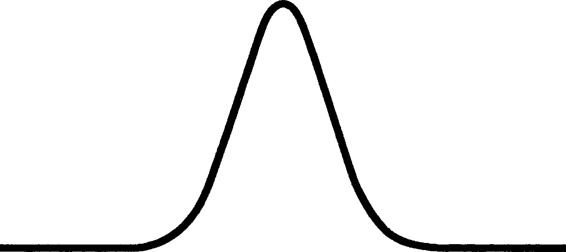
Мы начали с простой ставки и пришли к чему-то абсолютно абстрактному. Начали с наблюдений и оказались в царстве математики. В математике вещи обретают абстрактную чистоту.
Но, поскольку чистых абстракций в природе не существует, пожалуйста, даже не пытайтесь постичь глубинный смысл фигуры на рисунке 10. Просто знайте, как ею пользоваться. Воспринимайте ее как градусник: не обязательно понимать, что означает температура, чтобы пользоваться показаниями градусника. Главное — знать соответствие между температурой и, скажем, комфортностью (или какими-то другими эмпирическими факторами). Шестьдесят градусов по Фаренгейту соответствуют приятной погоде; минус десять — не то, о чем следует мечтать. Не обязательно интересоваться действительной скоростью столкновений между частицами, которая помогла бы уяснить подоплеку понятия "температура". Градусы — это некое подсобное средство, с помощью которого ваше сознание может перевести какие-то внешние явления на уровень чисел. Вот и гауссиана устроена так, что 68,2 процента наблюдений сосредоточиваются между минус одним и плюс одним стандартным отклонением от среднего. Я повторю: даже не пытайтесь понять, является ли стандартное отклонение средним отклонением — нет, не является, и многие (слишком) многие люди, использующие термин стандартное отклонение, этого не понимают. Стандартное отклонение — это вопрос простого соотношения, обычное число, с которым соизмеряются явления, если они действительно из разряда "гауссовых".
Стандартное отклонение часто называется сигмой. Также говорят о дисперсии (дисперсия — это сигма в квадрате).
Обратите внимание на симметричность "колокола". Одинаковый результат получается при отрицательной и при положительной сигме. Шансы спуститься ниже минус четырех сигм равны шансам перевалить через четыре сигмы, у нас они 1 к 32 000.
Как видите, основная идея "гауссовой кривой" (о чем я говорил выше) в том, что большинство наблюдений колеблется в рамках заурядного, среднего, в то время как шансы отклонения сокращаются быстрее и быстрее (экспоненциально), чем дальше вы уходите от центра. Если хотите ухватить главное, вот оно: резкое ускорение падения шансов при удалении от середины. Вероятность аномалий стремительно уменьшается. Ими можно спокойно пренебречь.
Из этого свойства вытекает высший закон Среднестана: поскольку большие отклонения чрезвычайно редки, их вклад в итог будет чрезвычайно мал.
В примере с замерами человеческого роста я брал за единицу отклонения десять сантиметров, показывая, как тает процент гигантов по мере увеличения роста. Это были отклонения на одну сигму; а еще ростовая таблица наглядно показывает, как происходит "соизмерение с сигмой", — ее использование в качестве единицы измерения.
эти утешительные постулаты
Выделим главные постулаты, определившиеся в ходе нашей игры в монетку, которая привела к протогауссовой, или рядовой, случайности.
Первый главный постулат: броски не зависят друг от друга. У монетки нет памяти. То, что вам выпали орел или решка, вовсе не означает, что в следующий раз вас ждет удача. Умение бросать монету не приходит со временем. Если ввести такой параметр, как память или мастерство бросания, вся эта гауссова конструкция зашатается.
Вспомним наши рассуждения из главы 14 о привязках и кумулятивном преимуществе. Обе теории утверждают, что сегодняшний выигрыш повышает шансы на выигрыш завтра. Поэтому вероятности зависят от истории и первый главный постулат, на котором строится гауссиана, в реальности не работает. В играх, конечно, прошлые выигрыши не должны увеличивать вероятность будущих, но в жизни это не так, и поэтому я такой противник обучения теории вероятности на примере игр. Если выигрыш влечет за собой дальнейший выигрыш, то у вас гораздо больше шансов стать свидетелем сорока выигрышей подряд, чем в пределах протогауссианы.
Второй главный постулат: "сумасшедших" прыжков не бывает. Размер шага, этого элементарного кирпичика классического случайного распределения, всегда известен: как раз один шаг. Он всегда определен. Мы не встречали ситуаций с "сумасшедшей" неравномерностью движений.
Помните, что, если один из этих двух главных постулатов отсутствует, ваши шаги (или подбросы монетки) не создадут в итоге гауссиану. При определенных обстоятельствах вы можете столкнуться с из ряда вон выходящей масштабно-инвариантной случайностью мандельбротовского типа.
"Вездесущесть гауссианы"
Всякий раз, когда я заявляю, что "гауссова кривая" вездесуща отнюдь не в реальной жизни, а только в умах статистиков, от меня требуют: "Докажи!" Как мы увидим в следующих двух главах, это сделать очень легко, а вот противоположное никому еще до сих пор доказать не удалось. Стоит мне высказать предположение, что существуют процессы, не описываемые гауссианой, меня просят это обосновать и, помимо фактов, "предъявить стоящую за ними теорию". В главе 14 мы рассматривали модель "деньги идут к деньгам", предлагавшуюся, чтобы оправдать неиспользование гауссианы. Разработчикам таких моделей приходится тратить уйму времени на подведение теоретической базы под возможные масштабируемые ситуации — как будто им надо за что-то извиняться. Теория-фигория! У меня с этим эпистемологическая проблема — с необходимостью оправдывать то, что миру не удается соответствовать идеализированной модели, которую сумел пропиарить какой-то слепец, отрешенный от реальности.
Я предпочитаю не моделировать возможные ситуации возникновения негауссовой случайности (впадая тем самым в грех слепого теоретизирования), а делать нечто противоположное: пристально изучать гауссиану и определять, где она действует, а где нет. Я знаю, где Среднестан. По-моему, именно приверженцы гауссианы часто (да что там — почти всегда) не вполне понимают, с чем они имеют дело, и должны обосновывать свои действия, а не наоборот.
Эта вездесущесть гауссианы — не свойство мира, а проблема, существующая в наших умах и вытекающая из нашего взгляда на мир.
В следующей главе мы обратимся к масштабируемости окружающего мира и к свойствам фрактала. А в той, что за ней, коснемся злоупотребления гауссианой в социоэкономике и "необходимости строить теории".
Я порой излишне горячусь, но только потому, что провел значительную часть своей жизни, размышляя над этой проблемой. С тех пор как я начал думать над ней и проводить разнообразные мысленные эксперименты вроде описанного выше, я тщетно искал вокруг себя, в мире бизнеса и статистики, кого-нибудь, кто был бы до конца интеллектуально последователен в смысле осознания угрозы Черного лебедя и отказа от гауссианы и ее инструментария. Многие, принявшие мою идею Черного лебедя, не смогли довести ее до логического завершения, а именно — не смогли признать, что нельзя использовать одну-единственную меру случайности, называемую стандартным отклонением (и называть ее "риском"); нельзя рассчитывать на простые ответы, когда речь идет о неопределенности. Отказ от гауссианы требует смелости, преданности истине и способности соединять разрозненные факты, требует желания глубже постичь случайность. И еще нужно не возводить чужую мудрость в абсолют.
Затем я начал знакомиться с физиками, которые отвергли гауссов подход, но стали жертвой другого заблуждения (иной формы платонизма), а именно — веры в точные предсказательные модели, эксплуатирующие в основном привязку из главы 14. Я не мог найти ни одного глубокого и технически подкованного ученого, который смотрел бы на мир случайности и понимал его природу, видел бы в расчетах подспорье, а не самоцель. Мне потребовалось около полутора десятилетий, чтобы открыть для себя такого мыслителя. Человека, сделавшего многих лебедей Серыми: Мандельброта — великого Бенуа Мандельброта.

