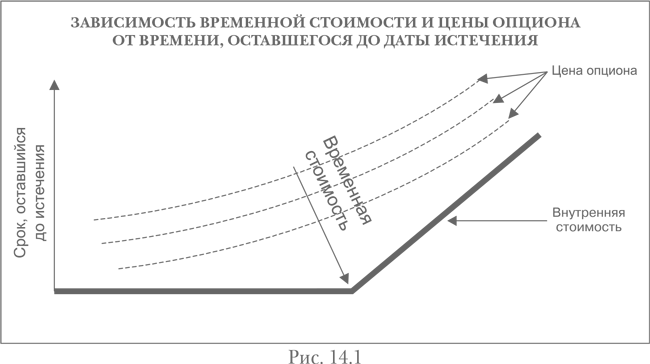
Премия опциона состоит из временной стоимости и внутренней стоимости. Внутренняя стоимость возникает только у опционов «при деньгах».

• Если опцион «при деньгах» и исполняется немедленно, внутренняя стоимость – это остаточная стоимость позиции.

• Временная стоимость – превышение стоимости опциона над ее внутренней составляющей – зависит от времени, оставшегося до истечения срока опциона и волатильности.

Тета измеряет чувствительность временной составляющей премии опциона к сокращению срока жизни опциона. Она представляет собой часть временной стоимости, которая амортизируется ежедневно. Например, если тета равна 2, а цена otm опциона равна 10, то за день он потеряет два тика и будет стоить 8 на следующий день.

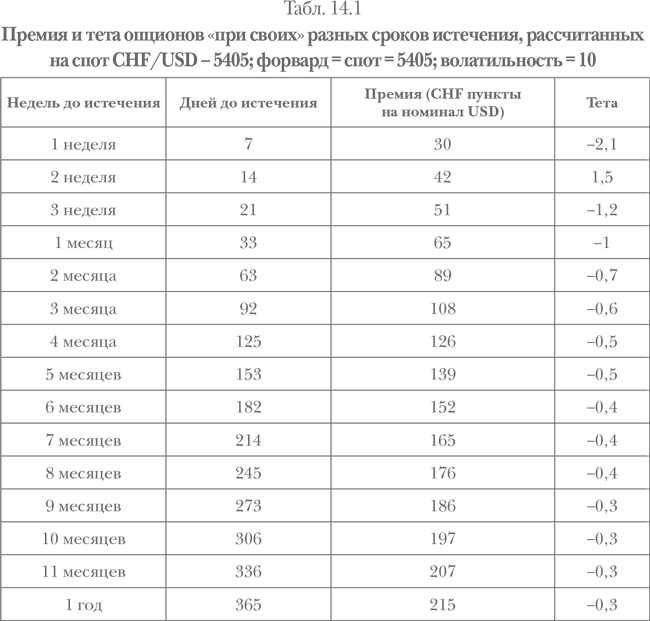
Премии опционов «при своих» с разными сроками истечения относятся друг к другу через квадратный корень срока опционов, приведенных к году, если рассчитывать, исходя из плоских кривых волатильности и форвардов (одинаковый своп для всех сроков). Например, премия десятидневного опциона относится к премии годового опциона в пропорции .

Зная премию опциона со сроком истечения, например, через 365 дней, можно найти стоимость премии опциона с другой срочностью. Более того, уровни тет данных опционов будут обратно пропорциональны отношению премий. Например, если премия опциона со сроком истечения 1 год (365 дней) равна 215, то премия опциона со сроком истечения 1 месяц (33 дня) равна 215 × √(33 ÷ 365) = 64,64.

В случае с тета 0,3 × √(365 ÷ 33) = 0,998.

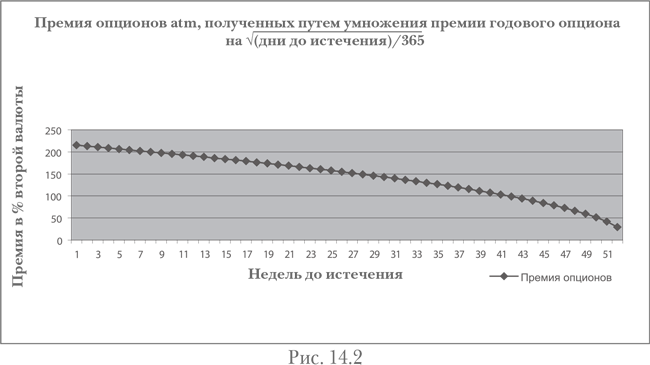
Несколько наблюдений из рис. 14.2:

1) График имеет форму функции квадратного корня.

2) Можно заключить, что, как и в случае веги:

a) 1-недельный atm-опцион (в среднем) будет терять стоимость в два раза быстрее, чем 1-месячный atm-опцион (оба рассчитаны для одинаковой волатильности); то же самое относится к парам: 1-месячный – 3-месячный и 3-месячный – 1-летний;

б) 1-летний atm-опцион потеряет только половину своей стоимости в первые девять месяцев своей жизни.

Зная математическое соотношение, можно объяснить и обобщить это наблюдение (только для опционов «при своих», при плоских кривых волатильностей и форвардов): премия уменьшается вдвое для периода в четыре раза короче, т. к. √¼ = ½.

Поскольку 365 ÷ 4 = 91, премия годового опциона равна atm-премии двойного номинала опциона, истекающего через 91 день.

3) Даже если опцион стоит дорого, это не означает, что он будет быстро терять стоимость. Более важна зависимость теты от времени, оставшегося до конца срока опциона. Чем меньше срок, тем быстрее амортизация премии опциона atm. Например, вы тратите $10 000 на один 1-недельный atm-опцион и на один 1-месячный atm-опцион. У 1-недельного опциона тета больше, и он будет терять стоимость быстрее. В конце недели стоимость 1-недельного опциона будет равна нулю, в то время как 1-месячный опцион сохранит свою стоимость. Срок опциона – такой же важный фактор при определении теты, как и размер премии.

График уменьшения временной стоимости, приведенный в табл. 14.1 и на рис. 14.2, действует только для опционов «при своих». Каждая «дельта» теряет свою стоимость по-своему. Например, краткосрочные 25-дельтовые опционы теряют свою дельту по более прямолинейному графику. Увядание же премии для опционов «глубоко в деньгах» (свыше 80 % дельты) или «далеко от денег» (ниже 20 % дельты) может вообще замедляться по мере приближения срока истечения опциона.

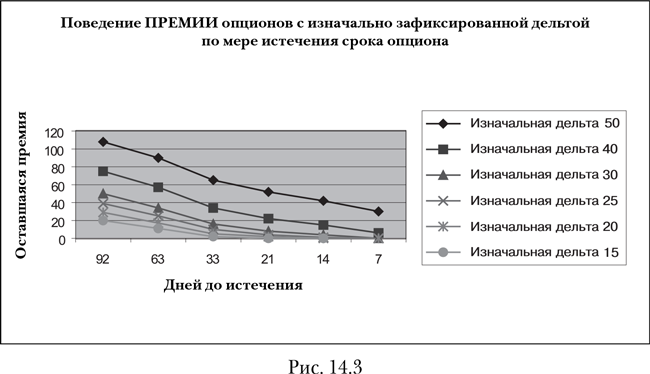
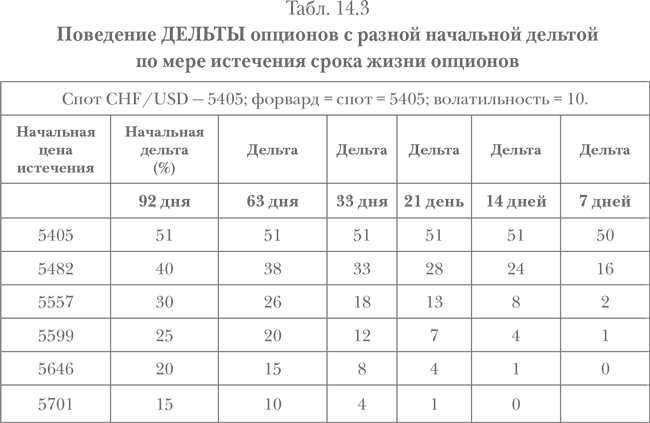
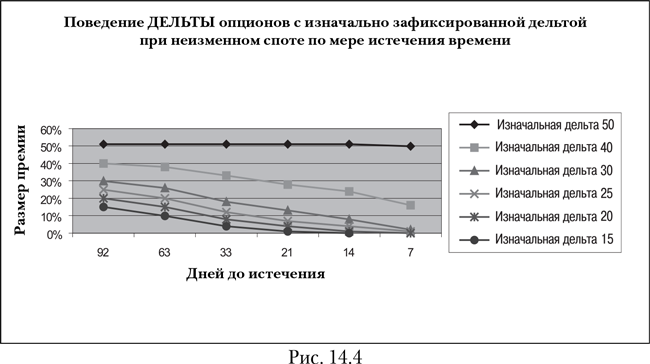
Табл. 14.2, 14.3 и рис. 14.3, 14.4 демонстрируют поведение премии опционов с изначально зафиксированными страйками (на уровне разных дельт) по истечении времени, а также влияние теты на дельту опционов.

Табл. 14.2 исключительно полезна для практиков, т. к. известные автору пособия не фокусируются на данных нюансах. Поэтому они полностью выпадают из поля зрения читателей.

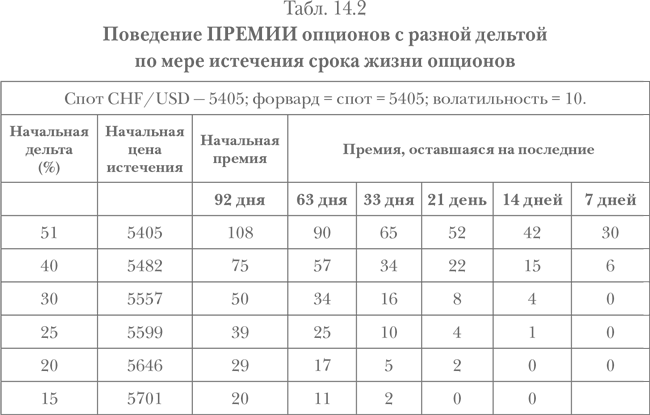
Обратите внимание:

1. Опцион с дельтой 20 потеряет больше половины своей стоимости в начале жизни, тогда как вид теты опциона с дельтой 30 будет ближе к тете atm-опциона, т. е. будет ускоренно терять стоимость ближе к сроку истечения! Иными словами, динамика потери стоимости опционов с разной дельтой – разная. Именно самые дешевые и наиболее рекомендуемые опционы теряют стоимость максимально быстро.

2. Амортизация премии у опционов с маленькой дельтой (или с большой дельтой) меньше в денежном выражении, чем у опционов «при своих». Например, у опционов, истекающих через 1 неделю, тета опциона пут с дельтой 25 % может быть равна 3,1, в то время как тета опциона пут с дельтой 50 % может составить 3,9.

Таким образом, если вы покупаете atm-опцион с номиналом $1 млн, его тета будет больше (больше амортизация премии) по абсолютному значению, чем у опциона «без денег» (или «при деньгах») с номиналом $1 млн.

Однако (!), сравнивая одинаковые инвестиции в опционы с низкой дельтой и atm, можно сказать, что первые теряют стоимость быстрее! Например, если вы потратили $1 млн на премию (а не купили опцион номиналом $1 млн) для покупки опциона «при своих», этот опцион потеряет меньше временной стоимости, чем опционы «без денег», купленные за $1 млн. Обратите внимание, что в первом случае вы покупаете опционы с одинаковой номинальной стоимостью, в то время как во втором вы делаете одинаковые инвестиции (разные номиналы) в опционы.

Таким образом, если в приведенном выше примере вы инвестируете 1 млн долл. в 2 млн номинала 25-дельтовых опционов, то за ночь они теряют 3,1 × 2. В то же время если бы вы купили за 1 млн долл. 1 млн номинала 50-дельтового опциона, то за ночь он теряет 3,9. Следовательно, стоимость ваших инвестиций падает быстрее при одинаковых инвестициях в опционы с меньшей дельтой.

Интуитивно это имеет смысл, т. к. инвестор может купить большее количество otm-опционов, чем опционов «при своих»! И они будут увядать быстрее! Таким образом, если вы: а) должны выбирать между инвестированием в atm-опцион с номиналом $1 млн или опцион номиналом $2 млн с дельтой 25 % и б) заинтересованы в сохранении стоимости опциона, то вы купите atm-опцион номинальной стоимостью $1 млн (и откажетесь от левериджа в $2 млн в пользу сохранения стоимости опциона).

3. Поскольку с истечением времени опционы с изначально низкой дельтой теряют дельту (т. е. возможность зарабатывать деньги на перехеджировании позиций) быстрее, на них сложно зарабатывать.

Амортизация премии у itm и otm-опционов с одним сроком и ценой исполнения должна быть одинаковой. Давайте еще раз логически обоснуем данное утверждение:

1) дельта-хеджированный опцион 1,4000 колл имеет то же соотношение риск/выгода, что и дельта-хеджированный опцион 1,4000 пут;

2) если соотношение риск/выгода одинаково для обеих позиций, вы заплатите одинаковый размер временной стоимости за оба опциона (хотя премии будут разные, т. к. премия itm-опциона включает внутреннюю стоимость);

3) поскольку тета показывает амортизацию временной стоимости (не внутренней стоимости), теты обоих опционов будут одинаковые.

Во многих пакетах программного обеспечения тета включает премию или дисконт в размере форвардного дифференциала (свопа). Например, если ставки доллара выше иены, то покупатель пута на доллар может увидеть заниженную тету, когда опцион захеджирован: хеджем на купленный пут является покупка долларов (продажа иен). А поскольку ставка доллара выше, хедж зарабатывает финансирование. Прибыль же за финансирование снижает тету.

В таких случаях правильнее было бы использовать термин «усушка» или time decay (временной распад), подразумевающий амортизацию премии под воздействием суммы теты и амортизации форварда.

1) а) Что дешевле купить: один 1-месячный atm-опцион или два 1-недельных опциона (один после истечения другого)?

б) Какую часть своей стоимости потеряет 1-месячный опцион за последнюю неделю своей жизни?

2) Вы купили 3-месячный atm-опцион номиналом $1 млн.

а) Какой номинал 1-месячных опционов вам надо продать, чтобы покрыть уплаченную вами премию?

б) Какова будет тета этой позиции (примите тету 3-месячного опциона за единицу)?

в) Какова вега этой позиции?

3) Ваш клиент купил опцион $10 млн номинала 1,2600 USD пут (CHF колл) и купил хедж $5 млн.

а) Если бы вместо этого он купил опцион USD колл с номиналом $10 млн и продал бы хедж $5 млн, изменилось бы поведение его позиции?

б) Учитывая прибыльность этих двух позиций, что вы думаете об их P&L и тетах?

в) Поскольку процентные ставки по долларам выше, чем по франкам, клиент получит дополнительный доход на первой позиции. Принимая во внимание разницу в прибыли, должны ли теты быть разными?

4) Клиент открывает позицию, которая будет стоить ему $1 млн. Какой срок и какую дельту ему следует выбрать, если он хочет, чтобы в конце срока его позиция:

а) хорошо сохранила стоимость;

б) имела большой леверидж?

5) Если премия опциона, истекающего через 306 дней, равна 197, какова премия опциона, истекающего через 182 дня?

6) Если тета опциона, истекающего через 63 дня, равна –0,7, какова тета опциона, истекающего через 153 дня?

1) а) Должны быть примерно одинаковы по цене.

б) Должен потерять около 50 % стоимости за последнюю неделю!

2) а) 2 млн;

б) в два раза больше;

в) такая же.

3) а) Получится точно такая же позиция.

б) Такие же. Для получения одинакового дохода надо понести одинаковые затраты.

в) Да. Тета позиции, у которой лучше вероятность заработать, должна быть больше. В противном случае возможен арбитраж, где две позиции с одинаковой доходностью имеют разные издержки.

4) а) Более длинный срок, ближе к atm;

б) более короткий срок, опцион с маленькой дельтой (otm).

5) 151,92 ÷ 197 × √(182 ÷ 306).

6) 0,45 ÷ (−0,7) ÷ √(153 ÷ 63).