III. Американские опционы. Опционы на фьючерсы, валюты, сырье, акции и облигации
1. Опционы американского стиля
В отличие от европейского опциона, который может быть исполнен лишь в конце своего срока действия, американский опцион может быть исполнен в любой момент на протяжении этого срока.
Один из способов оценки американских опционов заключается в использовании для этого биномиальных деревьев. Рассмотрим метод на примере вычисления цены американского колл-опциона на бездивидендную акцию.
Период действия опциона разобьем на малые отрезки времени длины dT. Предположим, что на каждом таком отрезке цена акции может от своего начального значения S либо с вероятностью p вырасти до Su, u > 1, либо с вероятностью 1 – p упасть до Sd, d < 1. Предположим также, что u = 1 /d, т.е. последовательные движения цены акции сперва вверх, а затем вниз компенсируют друг друга.
Значения u и p определяются из вероятностных соображений. В модели Блэка — Шолца цена акции в момент времени t + dT S(t + dT) есть логнормальная случайная величина с параметрами (lnS + (r – σ2/2) × dT, σ × √dt ), где S — цена акции в момент t. Исходя из этого можно вычислить математическое ожидание и дисперсию случайной величины S(t + dT), которые оказываются равными S × er × dT и S2 × e2r × dT ( eσ2 × dT – 1) соответственно.
В рассматриваемой нами модели S(t+dT) представляет собой дискретную случайную величину, с вероятностью p, равную Su, и с вероятностью 1 – p, равную Sd (ее математическое ожидание есть pSu + (1 – p)Sd, а дисперсия pS2u2 + [(1 – p)S2d2 – S2(pu + (1 – p)d)]. Чтобы такое приближение было наиболее точным, нужно, чтобы у этих двух случайных величин — дискретной и логнормальной совпадали математические ожидания и дисперсии. В таком случае для u, p и d с большой степенью точности выполняются равенства
p = (er× dT – d) /(u – d),
u = 1 /d = eσ × √dT.
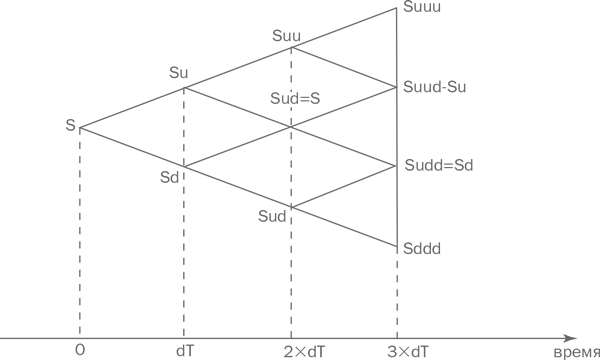
Зная значения u и d, можно построить дерево, описывающее возможную динамику цены акции на период действия опциона.
В нулевой вершине стоит цена акции в начальный момент времени — S, i-й ярус дерева соответствует моменту времени i × dT и содержит i + 1 возможную цену акции в этот момент S × uj × di–j , j = 0... Для вычисления цены опциона осуществляется процедура «спуска» по дереву от последнего яруса к нулевому, т.е. от момента исполнения к начальному моменту времени.
В вершинах последнего яруса записаны цены акции в момент исполнения опциона, из которых легко получить стоимость опциона в момент исполнения по формуле max[(S(T) – K)]. Зная цену опциона на (s + 1)-м ярусе, можно найти его цену на s-м ярусе, т.е. в предыдущий момент времени. Продемонстрируем это на примере.
Пусть уже вычислена цена опциона в точках Suu и Sud — X и Y соответственно. В точке Su у покупателя опциона есть две возможности: либо немедленно исполнить опцион и получить прибыль A = max(Su – K,0), либо не исполнять его, и тогда через время dT с вероятностью p он будет стоить X и с вероятностью (1 – p) – Y, а значит, дисконтированная на текущий момент времени средняя ожидаемая стоимость есть B=e–r × dT × (p × X + (1 – p) × Y). Поскольку покупатель опциона стремится максимизировать свою прибыль, он, разумеется, выберет наиболее выгодный из этих вариантов, поэтому цена опциона в точке Su будет равна max(A,B).
Двигаясь от яруса к ярусу по этому алгоритму, мы в конечном итоге найдем интересующую нас цену опциона в начальный момент времени.
На практике для установления точной цены достаточно 19–21 итераций (ветвей дерева). Дальнейшие итерации незначительно уточняют цену, но замедляют расчеты.
2. Опционы на валюту
В случае опционов на валюту роль непрерывно начисляемых дивидендов играет ставка доходности в валюте — rf. Формула для цены опциона на валюту получается из формулы цены опциона колл на акцию с дивидендами (см. приложение I) простой заменой q на rf.

Стоимость опциона пут на валюту равна:
P2 = K × e–r T × N(–d2) – S2 × e–rf T × N(–d1).
Здесь S2 — текущий курс валюты, а величины d1 и d2 определяются следующим образом:
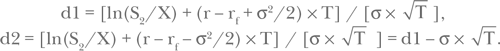
В теории хеджирования с использованием опционов на валюту, в дополнение к имеющимся «грекам» рассматривается производная цены опциона по ставке доходности в валюте — rf. Этот параметр называется Phi и вычисляется по следующей формуле:
Phi = –T × e-rf T × S2 × N(d1) — для опциона колл.
Phi = –T × e-rf T × S2 × N(–d1) — для опциона пут.
3. Опционы на фьючерсы
До настоящего времени мы говорили о цене опционов на спот. При оценке опциона на фьючерс используется только безрисковая ставка, которая играет роль ставки доходности. Формула для цены имеет следующий вид:

Стоимость опциона пут на фьючерс равна
P3 = e–r T × [ K × N(–d2) – F × N(–d1)].
Здесь F — текущая цена фьючерса, а величины d1 и d2 определяются следующим образом:
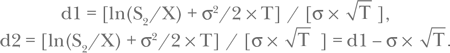
4. Сравнительная таблица формул опционов на акции, облигации, драгоценные металлы, нефть, базовые металлы

В этой табл.:
K — цена исполнения опциона;
S, S1 — цена акции;
S2 — курс валюты;
F — цена фьючерса на акцию, облигацию, нефть, металлы;
G — цена золота;
r — безрисковая ставка доходности;
q — непрерывная ставка дивидендов;
rf — ставка доходности в валюте;
rl — lease rate (ставка за заем физического золота);
d1, d2 — рассчитываются для каждого типа опциона по соответствующим формулам.

