I. Математические модели, лежащие в основе опционов

Ознакомившись с формулами, на основании которых оцениваются опционы и управляются опционные позиции, читатель приобретет психологическую уверенность, поскольку отсутствие пробелов в знаниях поможет избежать грубых ошибок в торговле. Но работа на финансовых рынках — это искусство, которое складывается из многих компонентов, лишь одним из которых является знание финансовой математики. Поэтому, хотя психологически важно ознакомиться с формулами, на которых базируются опционы, большинство практиков согласится, что знание формул не является необходимой составляющей успеха.

1. Базовые понятия. Выведение формулы опциона колл

Начнем с рассмотрения стандартного европейского опциона колл (call). Это контракт, дающий владельцу право в определенный момент времени купить определенный актив по определенной цене (цене исполнения).

Опционный контракт является правом, но не обязательством для его владельца. Поэтому, если владелец опциона считает, что исполнение опциона по оговоренной в контракте цене убыточно для него, он может контракт не исполнять. В этом случае неисполненный опционный контракт истечет.

Цену опциона (С) в настоящий момент определяют:

T — время, оставшееся до исполнения опциона (time to maturity);

S — цена спот актива в настоящий момент (spot price);

K — цена исполнения опциона или страйк (strike);

r — непрерывно начисляемая безрисковая процентная ставка (conti­nuously compounded risk-free rate);

S(T) — цена актива в момент исполнения опциона;

σ — волатильность (изменчивость) цены актива (volatility).

Рассмотрим эти параметры.

Единицей измерения времени (Т) является год. Если до исполнения опциона осталось D дней, то Т вычисляется по формуле:

T = D /365.

Модель Блэка — Шолца была первой моделью для оценки опционов. Она использует в качестве базового актива акции. Модель предполагает, что в момент исполнения опциона цена актива является логнормальной случайной величиной, т.е. логарифм отношения цен актива в текущий момент и в момент исполнения опциона имеет нормальное распределение. Это предположение довольно точно описывает реальные данные и позволяет в текущий момент оценить стоимость актива в будущем. В частности, исходя из него можно найти среднее значение цены актива и вероятность для нее подняться выше определенного уровня.

Для выведения формулы цены опциона Блэк, Шолц и Мертон вывели формулу стоимости акции. Она зависит от времени, оставшегося до исполнения опциона, цены базового актива в настоящий момент, непрерывно начисляемой безрисковой процентной ставки, а также еще одного параметра — волатильности актива.

σ — волатильность актива — параметр, характеризующий изменчивость цены актива.

Цена актива с большей волатильностью подвержена большим изменениям, нежели цена актива с меньшей волатильностью. В реальной жизни волатильность актива меняется в разные моменты времени, однако в данной модели мы считаем ее постоянной на протяжении всего срока действия опциона.

В момент исполнения опциона возможны две ситуации:

1) S(T) > K, т.е. цена базового актива выше цены исполнения — в таком случае прибыль от исполнения опциона равна S(T) – K [актив покупается по цене K, а затем немедленно продается по текущей цене S(T)].

2) S(T) ≤ K, т.е. цена базового актива ниже цены исполнения — тогда исполнять опцион не имеет смысла, поскольку не дороже будет купить актив по текущей цене. Прибыль от исполнения в этом случае равна 0.

Следовательно, прибыль от исполнения опциона составляет

max[0,S(T) – K].

Возможная прибыль от исполнения опциона на сегодняшний момент времени составляет:

max[0, S(T) – K] × e–rT ,

где e–rT — дисконтный фактор, приводящий будущую стоимость к сегодняшней. Возможная прибыль равна внутренней стоимости, умноженной на дисконтный фактор.

Поскольку цена актива — случайная величина, то цена опциона в настоящий момент времени или текущая премия равняется математиче­скому ожиданию возможной прибыли:

C = E{e–rT × max[0, S(T) – K)]}.

После подстановки вместо S(T) логнормальной случайной величины и проведения математических выкладок, связанных с вычислением математического ожидания, мы получаем формулу Блэка — Шолца для европейского опциона колл на акцию без начисления дивидендов:

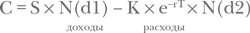
Здесь N(x) — функция распределения стандартной нормальной случайной величины; ее можно определить из таблицы стандартного нормального распределения.

Величины d1 и d2 находятся из следующих равенств:

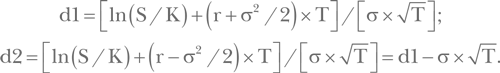
N(d2) — вероятность того, что опцион будет исполнен, тогда:

K × e–rT × N(d2) — дисконтированные средние ожидаемые затраты по исполнению опциона;

S × N(d1) — дисконтированное среднее ожидаемое значение цены акции в момент исполнения опциона.

Таким образом, первое и второе слагаемые исходят из ваших средних ожидаемых доходов и расходов при исполнении опциона.

2. Параметры цены опциона

Из формулы Блэка — Шолца вытекает, что цена опциона зависит от следующих параметров:

r — непрерывно начисляемая безрисковая процентная ставка;

T — время, оставшееся до исполнения опциона;

S — цена акции в текущий момент;

K — цена исполнения опциона;

σ — волатильность акции.

Выясним, как исходные параметры влияют на цену колл-опциона. Для этого рассмотрим изменения каждого параметра, предположив, что остальные остаются постоянными.

Зависимость цены от страйка

С уменьшением K цена возрастает, так как опцион колл с меньшей ценой исполнения предпочтителен, поскольку предоставляет возможность купить актив по более низкой цене. Опцион с меньшим значением K стоит дороже не только потому, что вероятность его исполнения больше, но и потому, что на его исполнении вы больше зарабатываете.

Зависимость цены от волатильности

Чем больше σ, тем сильнее отклоняется цена акции от некоего среднего значения. С ростом цены акции возможная прибыль по опциону неограниченно возрастает, при уменьшении же цены убытки ограничены заплаченной премией, поскольку вы не обязаны исполнять опцион в убыток себе. Отсюда следует: опцион на актив с большей волатильностью должен стоить больше опциона на актив с меньшей волатильностью.

Зависимость цены от времени, оставшегося до исполнения опциона

Время, оставшееся до исполнения опциона, влияет на цену акции похожим образом. Действительно, чем больше времени до исполнения, тем больше вероятность того, что цена поднимется, и тем больше вероятность получить большую прибыль при исполнении опциона. Учитывая, что наши убытки при падении цены на акцию ограничены, становится очевидным, что с приближением к времени исполнения цена опциона уменьшается. С уменьшением времени уменьшается также и дисконтирующий множитель, приводящий будущую прибыль к сегодняшнему значению. Это увеличивает стоимость опциона, однако в меньшей степени.

Зависимость цены от изменения цены базового актива

С увеличением цены акции увеличиваются ваши ожидания того, что в момент окончания действия опциона его исполнение принесет прибыль. Следовательно, с увеличением цены актива цена опциона колл возрастает.

Зависимость цены от безрисковой ставки

С увеличением безрисковой ставки увеличиваются ваши ожидания относительно будущей цены базового актива, следовательно, с увеличением процентной ставки цена опциона колл увеличивается.

3. Влияние на модель фактора дивидендов

Теперь перейдем к вычислению цены европейского опциона колл для акции, по которой выплачиваются дивиденды. После выплаты дивидендов цена акции уменьшается. Мы предполагаем, что она уменьшается ровно на величину выплачиваемых дивидендов. Следовательно, при оценивании опциона на эту акцию необходимо учитывать будущие уменьшения ее цены. В случае европейского опциона колл предполагается, что цена акции состоит из двух компонент — рисковой и безрисковой.

Безрисковая компонента — это дисконтированная величина всех дивидендов, которые будут выплачены по этой акции до момента исполнения опциона. Сделав предположение о будущих дивидендах и отняв их от сегодняшней цены, можно найти рисковую компоненту. Цена опциона на такую акцию вычисляется как цена опциона на рисковую компоненту. В этом случае мы подставляем в формулу Блэка — Шолца вместо S величину рисковой компоненты. Если DVD (discounted value of dividends) — дисконтированное значение всех дивидендов, выплачиваемых по акции в период действия опциона, то рисковая компонента равна S – DVD.

Если рассматривать опционы на индекс, то выплата дивидендов по акциям, входящим в этот индекс, происходит довольно часто. В этом случае с большой степенью точности можно считать, что дивиденты выплачиваются непрерывно.

Пусть нам нужно вычислить цену европейского колл-опциона на акции компании ААА, по которым непрерывно начисляются дивиденды по ставке q, и текущая цена которых S1. Через время Т, т.е. в момент исполнения опциона, средняя ожидаемая цена акции ААА будет не erT (как было бы в случае отсутствия дивидендов), а e(r–q)T.

Рассмотрим дополнительно акции идентичной компании ВВВ, по которым не выплачиваются дивиденды, и текущая цена которых S1 × e–qT. Через время T средняя ожидаемая цена акции ВВВ будет равна S1 × e–qT × erT = S1 × e(r–q)T, т.е. акции в среднем будут стоить одинаково, а по­скольку компании идентичны, то отклонение цены их акций от среднего значения также будет одинаковым.

Следовательно, в момент исполнения опциона акции будут иметь одинаковую стоимость, а значит, исполнение опционов на эти акции с одинаковыми страйками должно либо принести одинаковую прибыль, либо не принести прибыли одновременно.

При условии безарбитражности рынка на текущий момент времени европейский опцион с одним и тем же страйком на обе акции стоит одинаково, и его цена может быть вычислена по формуле Блэка — Шолца для акции без дивидендов после подстановки в нее S1 × e–qT вместо S.

Итак, C1 — цена опциона колл на акцию с дивидендами имеет следующий вид:

Величины d1 и d2 находятся из следующих равенств:

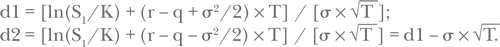
4. Цена опциона пут. Формула паритета пут/колл

Пока мы рассматривали только опцион колл. Теперь перейдем к рассмотрению опциона пут. Владелец опциона пут имеет право в определенный момент времени продать актив по заранее оговоренной цене. Как и в случае опциона колл, владелец может не исполнять опцион, если его исполнение для него невыгодно.

При расчете премии, выплачиваемой по опциону пут на акцию без дивидендов, можно использовать формулу паритета пут/Колл (put/call parity). Эта формула описывает зависимость между величинами премии по опционам пут и Колл на один и тот же базовый актив, имеющим одинаковый страйк K и время до исполнения Т.

Для вывода зависимости рассмотрим два портфеля.

Первый состоит из одного опциона колл и K × e–rT долларов, которые мы вкладываем под процент r на время T.

Второй состоит из одного опциона пут и одной акции.

Рассмотрим стоимость портфелей в момент исполнения опционов при разных значениях цены на акцию в тот момент времени S.

Первый портфель:

S(T) > K.

В этом случае после исполнения опциона мы получим прибыль S(T) – K, а вложенные в начале периода K × e–rT долларов вырастут до K долларов. Следовательно, стоимость портфеля равна

S(T) – K + K = S(T),

S(T) < K.

В этом случае исполнение опциона невыгодно. Следовательно, стоимость портфеля равна стоимости денег, т.е. K.

S(T) = K.

В этом случае при исполнении и при неисполнении опциона мы получаем одинаковую сумму: S(T) = K.

Второй портфель:

S(T) > K.

В этом случае продажа акции по цене K невыгодна, так как текущая цена выше. Стоимость портфеля равна стоимости одной акции, т.е. S.

S(T) < K.

В этом случае мы исполняем опцион и продаем акцию по цене K, которая выше текущего курса. Стоимость портфеля равна K.

S(T) = K.

В этом случае при исполнении и при неисполнении опциона мы получаем одинаковую сумму: S(T) = K.

Нетрудно заметить, что в момент исполнения опционов оба портфеля имеют одинаковую стоимость при любом значении цены акции. Условие безарбитражности рынка позволяет сделать вывод, что и в данный момент оба портфеля должны стоить одинаково, т.е.

C + K × e–rT = P + S.

Здесь

S — текущая цена акции;

K — цена исполнения опционов;

C — стоимость опциона колл;

P — стоимость опциона пут.

Полученное равенство называется формулой паритета колл/пут.

Исходя из нее, получаем, что цена опциона пут на акцию без дивидендов равна:

P = K × e–r T × N(–d2) – S × N(–d1),

где d1 и d2 такие же, как в формуле для цены опциона колл на акцию без дивидендов.

Если на акцию начисляются дивиденды по ставке q, то цена опциона пут равна:

P1 = K × e–r T × N(–d2) – S × e–q T × N(–d1),

где d1 и d2 такие же, как в формуле для цены опциона колл на акцию с непрерывно начисляемыми дивидендами.

Вопросы

1) Рассматривается акция, по которой непрерывно начисляется дивиденд по ставке q = 5%. Текущая цена акции $50, волатильность 60%, непрерывно начисляется безрисковая ставка 7%. Найдите вероятность исполнения трехмесячного европейского опциона колл на эту акцию в случаях, когда цена исполнения составляет $40 и $60.

2) Инвестор приобрел 5 полугодовых европейских опционов колл на акцию, по которой не выплачиваются дивиденды. Определите средние затраты инвестора по исполнению опциона колл, если известны следующие данные:

• цена акции в настоящий момент $50;

• цена исполнения опционов $60;

• волатильность акции и безрисковая ставка на следующие полгода равны 70% и 8% соответственно.

3) Рассмотрим трехмесячный опцион колл на акции без дивидендов. Текущая цена акции $50, цена страйк $49, безрисковая ставка — 5%. Сколько стоит трехмесячный опцион пут на эту акцию с таким же значением страйк, если опцион колл стоит $5?

ответы

1) Сначала рассмотрим опцион с ценой исполнения $40. Вероятность его исполнения равна N(d2).

d2 = [ln(S /K) + (r – q – σ2/2) × T] /[σ × √T] =

= [ln(50 /40) + (0,07 – 0,05 – 0,36 /2) × 0,25] /[0,6 × 0,5] =

= [0,223 – 0,04] /[0,3] = 0,61.

N(d2) = N(0,61) = 0,7291.

Для K = $60 имеем:

d2 = [ln(S /K) + (r – q – σ2/2) × T] /[σ × √T] =

= [ln(50 /60) + (0,07 – 0,05 – 0,36 /2) × 0,25] /[0,6 × 0,5] =

= [– 0,182 – 0,04] /[0,3] = – 0,74.

N(d2) = N(– 0,74) = 0,2296.

2) В случае исполнения опционов инвестор должен будет потратить 5 × $60 = $300 на покупку акций. В случае неисполнения опционов затраты инвестора равны 0. Средние затраты AC (average costs) будут равны затратам на исполнение, умноженным на вероятность исполнения опционов.

AC = 300 × N(d2).

В данной задаче:

S = 50;

K = 60;

r = 8% = 0,08;

σ = 70% = 0,7;

T = 0,5.

d2 = [ln(S /K) + (r – σ2/2) × T] /[σ × √T] =

= [ln(50/60) + (0,08 – 0,49/2) × 0,5] /[0,7 × 0,707] =

= [–0,182 – 0,083] /[0,495] = –0,54.

N(d2) = N(–0,54) = 1 – N(0,54) = 0,2946.

AC = 300 × 0,2946 = 88,38.

3) Из паритета пут-Колл P = C + K × e–rT – S = 5 + 49 × e–0,05 × 0,25 – 50 = 5 + 48,39 – 50 = 3,39.