Приложение 4
Одна из теорем в «Началах» доказывает, что если у двух треугольников одинаковые углы, эти треугольники подобны. А это значит, что форма у этих треугольников совершенно одинаковая и длины сторон соответственно пропорциональны. Если одна сторона одного треугольника вдвое длиннее соответствующей стороны второго треугольника, то это справедливо и по отношению к остальным сторонам.
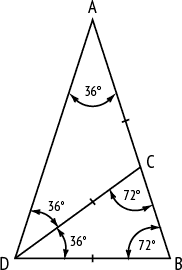
Треугольники ADB и DBC подобны, поскольку у них одинаковые углы. Следовательно, отношение AB/DB, то есть отношение сторон треугольников ADB и DBC, равно DB/BC, то есть отношению оснований этих треугольников.
AB/DB= DB/BC.
Однако эти треугольники также равнобедренные, поэтому
DB= DC= AC.
Из вышеприведенных равенств следует, что
AC/BC= AB/AC,
Что означает (согласно определению Евклида), что точка C делит отрезок AB в золотом сечении. Поскольку AD = AB и DB = AC, получаем также, что AD/DB = φ.
Приложение 5
Квадратные уравнения – это уравнения, имеющие вид
ax2 + bx+ c= 0,
где a, b, c – произвольные числа. Например, в уравнении 2x2 + 3x+ 1 = 0 имеем a = 2, b = 3, c = 1.
Общая формула для поиска двух корней уравнения:

В вышеприведенном примере
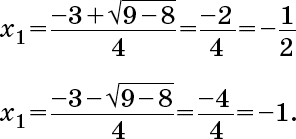
В уравнении, описывающем золотое сечение,
x2 – x – 1 = 0,
a = 1, b = –1, c = –1, следовательно, корни:
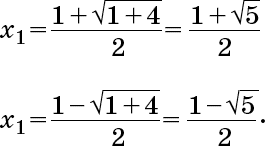
Приложение 6
Задачу о дележе наследства можно решить следующим образом. Обозначим все наследство как E, а долю каждого из сыновей в безантах – как x (по условию, все они делят наследство поровну).
Первый сын получил
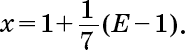
Второй сын получил
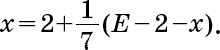
Приравниваем их доли:
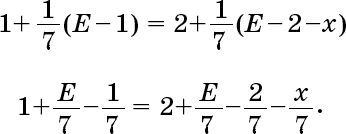
Упрощаем:
x/7 = 6/7
x= 6.
Следовательно, каждому из сыновей досталось по 6 безантов.
Подставив эту величину в первое равенство, получаем:
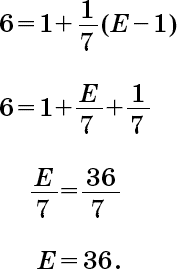
Сумма наследства составила 36 безантов. Следовательно, количество сыновей 36/6 = 6.
А вот как выглядит решение Фибоначчи.
Сумма наследства должна представлять собой такое число, чтобы если прибавить к нему 1 раз по 6, одно делилось бы на 1 плюс 6, то есть на 7, а если прибавить к нему 2 раза по 6, оно делилось бы на 2 плюс 6, то есть на 8, если же прибавить к нему 3 раза по 6, оно делилось бы на 3 плюс 6, то есть на 9, и т. д. Такое число – 36. 1/7 от (36 – 1/7) – это 35/7, плюс 1 – это 42/7, или 6, и это и есть сумма, которую получил каждый из сыновей; общая сумма наследства, поделенная на долю каждого из сыновей, дает нам число сыновей, то есть 36/6 равно 6.
Приложение 7
Отношение между количеством субобъектов n, коэффициентом сокращения длины f и числом измерений D равно
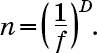
Если положительное число А записывается в виде А = 10L, то L мы называем логарифмом (по основанию 10) числа А и записываем это так: L = log A. Иначе говоря, равенства А = 10L и L = log A тождественны. Правила логарифмов таковы:
1. Логарифм произведения есть сумма логарифмов:
log (A × B) = log A+ log B.
2. Логарифм отношения есть разность логарифмов
log ( A/B ) = log A – log B.
3. Логарифм степени числа – это степень, умноженная на логарифм числа:
log Am = m× log A.
Поскольку 100 = 1, по определению логарифма log 1 = 0. Поскольку 101 = 10, 102 = 100 и так далее, получаем, что log 10 = 1, log 100 = 2 и т. д. Следовательно, логарифм любого числа от 1 до 10 – это число от 0 до 1, логарифм любого числа от 10 до 100 – это число от 1 до 2 и т. д.
Если мы возьмем логарифм (по основанию 10) обеих частей вышеприведенного равенства (описывающего отношения между n, f и D), то получим
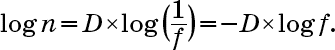
Если теперь поделить обе части на log f, мы получим
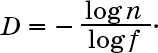
Скажем, в случае снежинки Коха каждая кривая содержит четыре «подкривые» в одну треть длины, поэтому n = 4, f = 1/3, и получаем
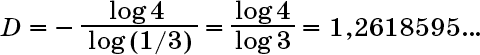
Приложение 8
Рассмотрим рис. 116, а, и увидим, что условие соприкосновения двух веток состоит в простом требовании, чтобы сумма всех горизонтальных длин постоянно уменьшающихся веток с длинами начиная от f 3 была равна горизонтальной составляющей большой ветки длиной f. Все горизонтальные составляющие – это общая длина, умноженная на косинус угла, величиной 30 градусов. Поэтому получаем
f× cos 30° = f3 × cos 30° + f4 × cos 30° + f5 × cos 30° + …
Поделим это выражение на cos 30° – и получим
f= f3 + f4 + f 5 + f6 + …
Сумма правой части – это сумма бесконечной геометрической прогрессии, то есть каждый ее член равен предыдущему, умноженному на константу, в которой первый член – это f 3, а отношение двух последовательных членов равно f. В целом сумма S бесконечной геометрической прогрессии с первым членом а и отношением последовательных членов q равна
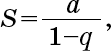
Например, сумма прогрессии
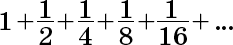
где a = 1 и q = 1/2, равна
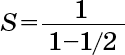
В нашем случае из вышеприведенного уравнения следует
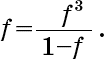
Делим обе части на f и получаем
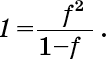
Умножаем на (1–f), сокращаем и получаем квадратное уравнение
f2 + f – 1 = 0,
положительный корень которого равен
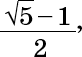
То есть 1/φ.

