Приложение 1
Мы хотим доказать, что для любых целых чисел p и q, таких, что p > q, три числа: p2 – q2; 2pq; p2 + q2 формируют пифагорову тройку. Иначе говоря, нам надо доказать, что сумма квадратов первых двух чисел равна квадрату третьего.
Для этого мы обратимся к общим формулам сокращенного умножения, справедливым для любых a и b:
(a + b)2 = (a + b) × (a + b)= a2 + ab + ba + b2 = a2 + 2ab + b2
(a – b)2 = (a – b) × (a – b)= a2 – ab – ba + b2 = a2 – 2ab – b2.
На основании этих формул квадрат первого числа равен
(p2 – q2)2 = p4 – 2p2q2 + q4.
Сумма первых двух квадратов равна
p4 – 2p2q2 + q4 + 4p2q2 = p4 + 2p2q2 + q4.
Квадрат третьего числа равен
(p2 + q2)2 = p4 + 2p2q2 + q4.
Итак, мы видим, что квадрат третьего числа равен сумме квадратов первых двух чисел независимо от значений p и q.
Приложение 2
Мы хотим доказать, что диагональ и сторона правильного пятиугольника несоизмеримы, то есть у них нет общей меры.
Общий принцип доказательства по методу reductio ad absurdum приведен в конце главы 2.
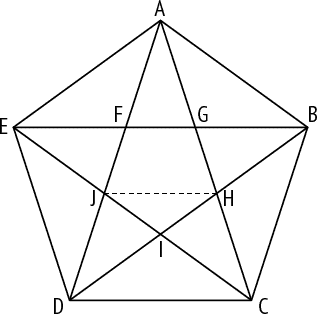
Обозначим сторону правильного пятиугольника ABCDE как s1, а диагональ – как d1. Из свойств равнобедренных треугольников легко вывести, что AB = AH и HC = HJ. Теперь обозначим сторону меньшего правильного пятиугольника FGHIJ как s2 и его диагональ как d2. Очевидно, что
AC= AH + HC= AB + HJ.
Следовательно,
d1 = s1 + d2 или d1 – s1 = d2.
Если у d1 и s1есть какая-либо общая мера, значит, и d1, и s1представляют собой целое произведение этой общей меры. Следовательно, существует также общая мера d1 – s1, то есть d2. Подобным же образом равенства
AG= HC= HJ
AH= AB
и
AH= AG+ GH
AB= HJ+ GH
дают нам
s1 = d2 + s2
или
s1 – d2 = s2.
Поскольку на основании нашего предположения общая мера для s1 и d1 представляет собой также общую меру для d2, последнее равенство доказывает, что она же еще и общая мера для s2. Поэтому мы обнаруживаем, что та единица, которая измеряет s1 и d1, измеряет также s2 and d2. Продолжать этот процесс можно до бесконечности, рассматривая правильные пятиугольники все меньшего и меньшего размера. Тогда мы получим, что та же единица, которая служит общей мерой стороны и диагонали первого правильного пятиугольника, служит общей мерой и для всех других пятиугольников, сколь бы крошечными они ни становились. Поскольку очевидно, что так быть не может, следовательно, наше первоначальное предположение, что у стороны и диагонали правильного пятиугольника есть общая мера, ложно, что и доказывает, что s1 и d1 несоизмеримы.
Приложение 3
Площадь треугольника равна половине произведения его основания на высоту, проведенную к основанию. У треугольника TBC основание BC равно 2а, а высота ТА равна с. Следовательно, площадь треугольника равна с × а. Мы хотим показать, что если квадрат высоты пирамиды h2 равен площади ее треугольной стороны s × a, то s/a равно золотому сечению.
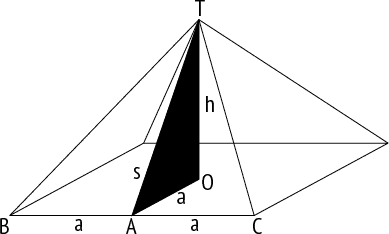
Дано, что
h2 = s× a.
Применив теорему Пифагора к прямоугольному треугольнику TOA, получаем
s2 = h2 + a2.
Теперь подставим значение h2 из первого равенства и получим
s2 = s× a + a2.
Разделим обе части на a2 и получим
(s/a)2 = (s/a)+ 1.
Иными словами, если мы обозначим s/a как x, у нас получится квадратное уравнение
x2 = x+ 1.
В главе 4 показано, что именно это уравнение и описывает золотое сечение.

