Золотая музыка
Пифагор открыл, что разные музыкальные тоны соотносятся между собой как рациональные числа, и этим открытием в наши дни пользуются все струнные квартеты и все симфонические оркестры. Более того, в перечень обязательных образовательных дисциплин, принятый у древних греков и оставшийся неизменным до времен Средневековья, музыка входила как раздел математики, а музыканты сосредотачивали свои усилия на понимании математической основы тонов. Концепция «музыки сфер» – великолепный синтез музыки и математики, и в воображении философов и музыкантов именно она позволяла – пусть и немногим избранным и одаренным – представить себе мироздание как единый величественный замысел. По словам великого римского оратора и философа Цицерона (ок. 106–43 гг. до н. э.) «звук, о котором говорилось выше, производимый необычайно быстрым круговращением всего мира, столь силен, что человеческое ухо не может его воспринять, – подобно тому, как вы не можете смотреть прямо на Солнце, когда острота вашего зрения побеждается его лучами» (Пер. И. Горенштейна). Лишь в XII веке музыка перестала рабски следовать математическим формулам и предписаниям. Однако даже в XVIII веке немецкий философ-рационалист Готфрид Вильгельм Лейбниц (1646–1716) писал: «Musica est exercitium arithmeticae occultum nescientis se numerare animi» («Музыка есть тайное арифметическое упражнение духа, который не знает, что он занят вычислениями»).
Примерно в это же время великий немецкий композитор Иоганн Себастьян Бах (1685–1750) необычайно увлекался разнообразными играми с участием чисел и музыкальных тонов. В частности, он при помощи музыкального шифра закодировал в некоторых своих сочинениях собственную подпись. Согласно старой немецкой системе записи нот буква В соответствовала си-бемоль, а H – си; А – это ля, С – до, поэтому Бах записал свою фамилию ВАСН нотами – си-бемоль, ля, до, си. Кроме того, Бах применял и шифр, основанный на Гематрии. Буквенное обозначение ноты ля – А – соответствует число 1, ноты си – В – числу 2, до – С – числу 3 и т. д., поэтому B-A-C-H = 14, а J-S-B-A-C-H = 41 (поскольку во времена Баха I и J в немецком алфавите были одной и той же буквой). Эрик Альтшулер, математик и большой любитель творчества Баха, в своей увлекательной книге «Баханалия» (Eric Altschuler. Bachanalia, 1994) приводит многочисленные примеры зашифрованных в музыке композитора чисел 14 (ВАСН) и 41 (JSBАCH); он убежден, что Бах сознательно употреблял именно такие последовательности нот. Например, тема первой фуги Баха, в фуге до-мажор из первого тома «Хорошо темперированного клавира», состоит из четырнадцати нот. Кроме того, из двадцати четырех повторений темы в двадцати двух она доведена до завершения, в двадцать третьем – почти до завершения и лишь в одном, четырнадцатом, вообще не завершена. Альтшулер делает вывод, что то, что Бах так увлеченно ставил в своих произведениях шифрованную подпись, сродни пристрастию художников включать автопортреты в создаваемые картины или манеры Альфреда Хичкока исполнять во всех своих фильмах маленькую роль-камео.
Если учесть исторические отношения музыки с числами, на ум сам собой приходит вопрос, играло ли золотое сечение (или числа Фибоначчи) ту или иную роль как в развитии музыкальных инструментов, так и в музыкальных композициях.
Золотое сечение очень часто применяется в конструкции скрипки. Как правило, очертания корпуса скрипки составляют не менее двенадцати кривых – они и создают ее характерные изгибы. Центром самой плоской кривой, внизу, как правило, служит точка, делящая центральную линию скрипки в золотом сечении.
Пожалуй, самые знаменитые скрипки – это инструменты работы Антонио Страдивари (1644–1737) из итальянского города Кремона. На чертежах мастера (рис. 85) видно, что Страдивари особенно тщательно рассчитывал геометрическое положение так называемых эфов – прорезей на передней части корпуса, – и помещал их в точки, определенные золотым сечением. Однако лишь немногие – возможно, таких и вовсе нет, – полагают, будто скрипки Страдивари обязаны своим непревзойденным качеством и звучанием именно золотому сечению. Гораздо чаще «секретом» Страдивари называют лак, клей, древесину и, конечно, мастерство изготовителя. Многие специалисты сходятся на том, что популярность скрипок XVIII века в целом объясняется их прекрасным звучанием в больших концертных залах. Большинство этих специалистов скажет вам также, что никакого «секрета» у скрипок Страдивари нет: это прекрасно выполненное изделие, которое вполне можно повторить, сумма тщательно изготовленных частей, составляющих добротное целое.
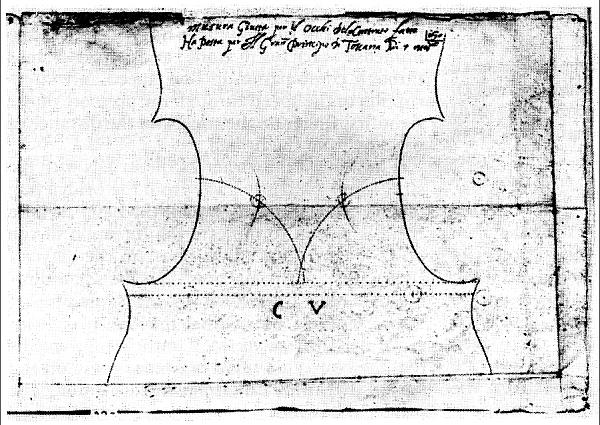
Рис. 85
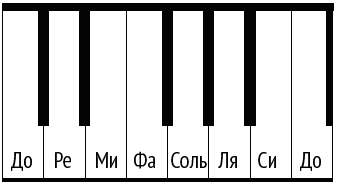
Рис. 86
В связи с числами Фибоначчи упоминают и другой музыкальный инструмент – фортепиано. Октава на клавиатуре фортепиано состоит из тринадцати клавиш, восьми белых и пяти черных (рис. 86). Черные клавиши, в свою очередь, объединены в две группы – две и три. Так вышло, что числа 2, 3, 5, 8 и 13 – последовательные числа Фибоначчи. А то, что главная тональность – до мажор, объясняется отчасти тем, что эту гамму играют только на белых клавишах. Однако очень может быть, что связь между клавиатурой фортепиано и числами Фибоначчи – всего лишь случайность, порождающая необоснованные домыслы. Во-первых, обратим внимание, что хроматическая гамма – на рисунке от ноты «до» до ноты «си» – на которой строится вся западная музыка, состоит на самом деле из двенадцати, а не тринадцати полутонов. Одна и та же нота «до» играется в октаве дважды, дабы подчеркнуть завершенность цикла. Во-вторых и в-главных, расположение клавиш в два ряда, когда диезы и бемоли сгруппированы по два и по три в верхнем ряду, восходит к началу XV века, то есть сложилась задолго до публикации книги Пачоли и тем более до любых серьезных исследований чисел Фибоначчи.
Страстные поклонники золотого сечения утверждают, что это соотношение обладает особыми эстетическими свойствами не только в изобразительном искусстве, но и в музыке, где оно создает особенно приятные созвучия. Например, в книгах о золотом сечении сплошь и рядом пишут, что многие считают, будто самые благозвучные музыкальные интервалы – это большая и малая сексты и что эти интервалы связаны с золотым сечением. Для чистого музыкального тона характерна определенная частота, выраженная в количестве колебаний в секунду, и определенная амплитуда, определяющая громкость в конкретный момент времени. Обычно для настраивания музыкальных инструментов используют ноту ля, которой соответствует частота 440 колебаний в секунду. Большая секста получается из сочетания ля с до: последней соответствует частота около 264 колебаний в секунду. Отношение частот 440/264 сокращается до 5/3 – то есть до отношения двух последовательных чисел Фибоначчи. Большая секста получается, если взять верхнее до (528 колебаний в секунду) и ми (330 колебаний в секунду). В этом случае отношение 528/330 сокращается до 8/5, то есть тоже до отношения двух последовательных чисел Фибоначчи – это уже очень близко к золотому сечению (напомню, что отношения последовательных чисел Фибоначчи стремятся к золотому сечению). Однако и здесь, как и в живописи, понятие «самого благозвучного» музыкального интервала несколько неоднозначно.
Инструменты, ноты у которых фиксированы, например, фортепиано, настраивают по «равномерно темперированному строю», который популяризировал Бах, где каждый полутон обладает таким же отношением частот, что и следующий, поэтому легко играть в любой тональности. Отношение двух соседних частот у хорошо темперированного инструмента равно 21/12 (то есть корень 12 степени из 2). Откуда взялось это число? Его происхождение восходит к Древней Греции. Вспомним, что октава получается, если поделить струну на две равные части (то есть соотношение частот должно быть 2 к 1), а квинта – если соотношение частот будет 3 к 2 (то есть при делении струны на две части – две трети и одна треть). Один из вопросов, особенно занимавших пифагорейцев, состоял в том, можно ли создать целое число октав, повторяя процедуру создания квинты (то есть последовательно применяя соотношение частот 3 к 2). В математических терминах это все равно что спросить, существуют ли два целых числа n и m, такие, что (3/2)n = 2m. Как выясняется, целых чисел, удовлетворяющих этому равенству, нет, однако при n = 12 и m = 7 мы подходим к решению довольно близко, ведь по странному совпадению 21/12 примерно равняется 31/19 (корень 19 степени из 3). Поэтому двенадцать частот октавы – это приблизительно равные степени базового соотношения частот 21/12. Кстати, хотите верьте, хотите нет, но 19/12 = 1,58, не так уж далеко от φ.
Золотое сечение в принципе могло бы повлиять на то, какое удовольствие мы получаем от музыкального произведения, если учесть концепцию пропорционального равновесия. Однако положение дел здесь несколько сложнее, чем в изобразительном искусстве. Неудачная композиция картины сразу бросается в глаза. С другой стороны, в музыке нужно выслушать произведение с начала до конца, а потом уже делать выводы. Тем не менее не приходится сомневаться, что опытные композиторы строят свои произведения так, чтобы не только разные части прекрасно гармонировали друг с другом, но можно было оценивать и каждую часть в отдельности – она служит сама себе мерилом.
Мы видели много примеров, когда приверженцы золотого сечения изучали пропорции всевозможных произведений искусства в поисках действительного или мнимого применения φ. Эти страстные поклонники подвергли подобному обращению и многие музыкальные композиции. Результаты получились очень похожие: наряду с единичными случаями, когда золотое сечение и в самом деле легло в основу той или иной системы пропорций, налицо множество ошибочных предположений.
Пол Ларсон из Университета Темпл в 1978 году заявил, что обнаружил золотое сечение в нотной записи первой европейской музыки – в хоралах «Kyrie» из собрания грегорианских хоралов «Liber Usualis». Тридцать хоралов «Kyrie» в этом собрании созданы с разбросом более чем в шестьсот лет, начиная с Х века. Ларсон утверждал, что проанализировал 146 частей хоралов «Kyrie» и в 105 из них обнаружил значимые «события» (например, начало или конец музыкальной фразы), разделенные в отношении золотого сечения. Однако в отсутствие каких бы то ни было исторических данных, подтверждающих, что композиторы тех времен применяли золотое сечение при создании этих хоралов, и каких бы то ни было рациональных объяснений, зачем это было делать, можно лишь считать, что перед нами, к сожалению, очередной пример жонглирования цифрами.
В целом подсчет нот и ритма нередко выявляет определенные численные соотношения между разными частями музыкальной пьесы, и у того, кто проводит этот анализ, возникает, конечно, понятное и естественное искушение сделать вывод, что композитор сознательно все рассчитал. Однако если нет надежных документальных свидетельств – а во многих случаях их нет – подобные предположения сомнительны.
В 1995 году математик Джон Ф. Путц из колледжа Альма в Мичигане исследовал вопрос о том, пользовался ли Моцарт (1756–1791) золотым сечением в двадцати девяти частях фортепианных сонат, каждая из которых, в свою очередь, состоит из двух отчетливо выраженных фрагментов: сначала идет экспозиция, когда слушателя знакомят с музыкальной темой, а затем разработка, где тема развивается и пересматривается. Поскольку музыкальные произведения делятся на одинаковые по продолжительности единицы под названием «такты», Путц изучил отношение количества тактов в двух частях сонат. Моцарт, который в школьные годы, по свидетельству его сестры, «не говорил и не думал ни о чем, кроме цифр», вероятно, один из лучших кандидатов на то, чтобы строить свои сочинения на математической основе. Более того, и до Путца было опубликовано несколько статей, где утверждалось, что в фортепианных сонатах Моцарта и в самом деле видно влияние золотого сечения. Первые результаты Путца оказались очень многообещающими. В сонате № 1 до мажор, к примеру, в первой части разработка состоит из шестидесяти двух тактов, а экспозиция из тридцати восьми. Отношение 64/38 = 1,63 очень близко к золотому сечению. Однако тщательное изучение всех данных в целом убедило Путца, что нет, Моцарт не применял в своих сонатах золотое сечение и вообще неочевидно, что простое соотношение длительности частей произведения делает его особенно приятным. Поэтому, хотя многие называют музыку Моцарта подлинно божественной, божественная пропорция тут ни при чем.
А вот знаменитый венгерский композитор Бела Барток (1881–1945), судя по всему, применял золотое сечение довольно часто. Бела Барток был не только пианистом-виртуозом, но и фольклористом и сочетал элементы, заимствованные у других композиторов, которыми он восхищался – в том числе, у Штрауса, Листа и Дебюсси – с фольклорными мотивами, что и придавало его музыке ярчайшую индивидуальность. Как-то раз Барток сказал, что «мелодический мир моих струнных квартетов если и отличается от народных песен, то несущественно». Ритмическая живость его музыки в сочетании с тщательно рассчитанной симметрией форм делает его одним из самых оригинальных композиторов XX века.
Венгерский музыковед Эрне Лендваи долго и внимательно изучал музыку Бартока и опубликовал об этом много книг и статей. Лендваи утверждает, что «стилистический анализ музыки Бартока позволил мне заключить, что главная черта его хроматической техники – подчинение законам золотого сечения в любом музыкальном движении». Согласно Лендваи, то, как Барток строит ритм своих композиций – превосходный пример применения золотого сечения в музыке. Анализируя, в частности, фугу из «Музыки для струнных, ударных и челесты» Бартока, Лендваи показывает, что 89 тактов фуги разделены пирамидальным пиком громкости на две части – 55 и 34 такта. Дальнейшее деление производится при помощи сурдины, приглушающей звук различных инструментов – начало и конец ее действия отмечают границы сегментов – и другими изменениями текстуры (рис. 87). Количество тактов всегда совпадает с числами Фибоначчи, а отношения между крупными частями близки к золотому сечению (например, 55/34). Подобным же образом в «Сонате для двух фортепиано и ударных» различные темы развиваются в порядке чисел Фибоначчи и согласно золотому сечению по количеству полутонов (рис. 88).
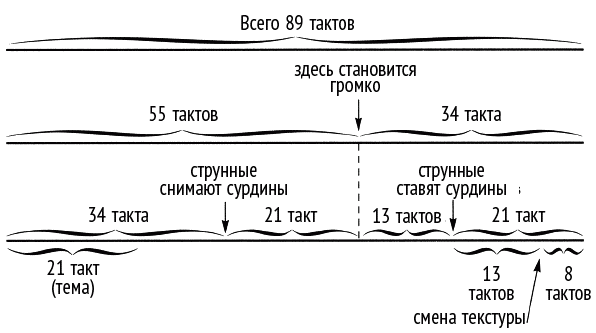
Рис. 87

Рис. 88
Не все музыковеды согласны с анализом Лендваи. Сам Лендваи признает, что Барток о своих композициях говорил очень мало, почти ничего: «Пусть моя музыка говорит сама за себя, я не претендую ни на какую интерпретацию своих работ». То обстоятельство, что Барток не оставил никаких черновиков, из которых следовало бы, что он математически выводил ритмы и соотношения, превращает любой анализ в гипотезу и не более того. Кроме того, Лендваи даже уклоняется от вопроса, сознательно ли Барток применял золотое сечение. Венгерский музыковед Ласло Сомфаи в своей книге «Бела Барток. Композиция, концепции и собственноручные документы» (Laszlo Somfai. Béla Bartók: Composition, Concepts and Autograph Sources», 1996) решительно опровергает гипотезу о том, что Барток опирался на золотое сечение. На основании тщательного анализа примерно 3600 страниц, занявшего тридцать лет, Сомфаи приходит к выводу, что Барток сочинял музыку безо всяких продуманных теоретических построений. Другие музыковеды, в том числе Рут Татлоу и Пол Гриффитс, также называют исследования Лендваи «сомнительным».
Рой Ховат из Кембриджского университета в своей занимательной книге «Дебюсси в пропорциях» (Roy Howat. Debussy in Proportion) отстаивает ту точку зрения, что французский композитор Клод Дебюсси (1862–1918), чье новаторство в гармонии оказало сильнейшее влияние на целые поколения композиторов, применял золотое сечение во многих своих произведениях. Например, в пьесе для фортепиано «Отражения в воде», входящей в цикл «Образы», первое повторение рондо происходит после такта 34, то есть в точке, которая делит отрывок пьесы с начала произведения до начала кульминации – такт 55 – в золотом сечении. Напоминаю, что и 34, и 55 – числа Фибоначчи, а отношение 34/21 – очень близкое приближение к числу φ. Та же структура зеркально повторена во второй части, разделенной в отношении 24/15 (что равно отношению двух чисел Фибоначчи 8/5 и опять же близко к золотому сечению, см. рис. 89). Подобные деления Ховат обнаруживает в трех симфонических эскизах «Море», фортепианной пьесе «Сады под дождем» и других произведениях.
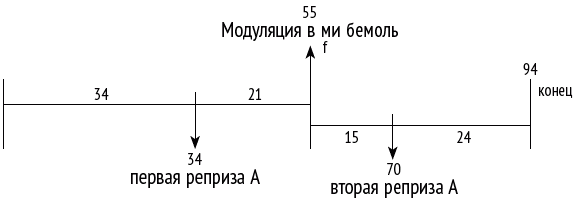
Рис. 89
Должен признать, что, учитывая историю создания «Моря», мне трудновато поверить, что Дебюсси при сочинении именно этого произведения опирался на какие бы то ни было математические соображения. Работать над «Морем» Дебюсси начал в 1903 году и в письме к своему другу Андре Мессаже писал: «Быть может, ты не знаешь, что мне была уготована судьба моряка и что по иному пути я пошел лишь случайно. Однако страстная любовь к нему [к морю] сохранилась у меня навсегда». Ко времени завершения «Моря» в 1905 году вся жизнь Дебюсси буквально перевернулась. Он ушел от первой жены Лили (Розали Тексье) к очаровательной Эмме Бардак, Лили пыталась покончить с собой, затем и Лили, и Эмма подали на композитора в суд. Если вслушаться в «Море» – вероятно, самое искреннее и страстное произведение Дебюсси, в ушах буквально раздается музыкальный портрет моря, вдохновленный, возможно, работами английского живописца Джозефа Мэлфорда Уильяма Тернера, однако очевидно, что это не только изобразительная музыка, но еще и выражение бурного периода в жизни композитора.
Поскольку сам Дебюсси особенно не распространялся о своих композиторских приемах, нужно провести четкое различие между навязанной интерпретацией и подлинными сознательными намерениями композитора, о которых мы ничего не знаем. В доказательство своего анализа Ховат приводит два внешних обстоятельства: во-первых, Дебюсси был тесно связан с художниками-символистами, о которых достоверно известно, что они интересовались золотым сечением, во-вторых, сохранилось письмо Дебюсси, написанное в августе 1903 года его издателю Жаку Дюрану. В этом письме, которое прилагалось к вычитанным гранкам «Садов под дождем», Дебюсси говорит, что в одном месте выпал такт, и объясняет: «Он, однако, необходим, так как имеет отношение к числу – к божественному числу». Напрашивается вывод, что Дебюсси основывал свои гармонические структуры не просто на численных расчетах, но что важную роль в этом играло некое «божественное число» (предполагается, что речь идет о золотом сечении).
Кроме того, Ховат считает, что на Дебюсси влияли сочинения математика, критика и искусствоведа Шарля Анри, который очень интересовался численными соотношениями в мелодии, гармонии и ритме. Работы Анри по эстетике, в том числе «Введение в научную эстетику» (Charles Henry. Introduction а une esthétique scientifique, 1885), уделяли золотому сечению очень важное место.
Вероятно, мы так никогда и не узнаем, действительно ли этот столп французского модернизма сознательно применял золотое сечение при построении формальных пропорций. Среди крайне немногочисленных учеников Дебюсси была мадемуазель Ворм де Ромийи, которая как-то раз написала, что он «всегда жалел, что вместо музыки не занялся живописью». Вероятно, в некоторой, пусть и небольшой степени весьма оригинальная эстетика Дебюсси и вправду строилась на золотом сечении, однако это, несомненно, был не главный источник творчества композитора.
Не удержусь и приведу курьезный исторический случай, в котором имена Бартока и Дебюсси оказались связаны. Во время визита молодого венгерского композитора в Париж великий фортепианный педагог Исидор Филипп предложил представить Бартока композитору Камилю Сен-Сансу, в то время очень знаменитому. Барток отказался. Тогда Филипп предложил познакомить его с великим композитором и органистом Шарлем-Мари Видором. Барток снова отказался. «Ладно, – сказал Филипп, – если вы не хотите встречаться с Сен-Сансом и Видором, с кем же вам угодно познакомиться?» – «С Дебюсси». – «Но он же кошмарный человек! – воскликнул Филипп. – Страшный мизантроп и наверняка обойдется с вами грубо. Неужели вы хотите, чтобы Дебюсси вас оскорбил?» – «Да!» – ответил Барток, не раздумывая.
Появление различных технологий звукозаписи и компьютерной музыки в ХХ веке упростило точные математические измерения и способствовало появлению музыки, основанной на числах. Например, австрийский композитор Альбан Берг (1885–1935) выстроил свой «Камерный концерт» целиком и полностью на числе три: там есть и объединение по тридцать тактов, и три темы, и три основные «краски» – фортепиано, скрипка, духовые. Французский композитор Оливье Мессиан (1908–1992), движимый в основном страстной католической верой и любовью к природе, также сознательно применял числа в ритмических конструкциях, например, при определении количества движений. Однако когда в 1978 году его прямо спросили, применял ли он при этом золотое сечение, он ответил, что нет.
Композитор, математик и преподаватель Иосиф Шиллингер (1895–1943) был весьма незаурядным человеком, его личность и мировоззрение служили ярким примером платоновского представления о связи математики с музыкой. Шиллингер учился в Петроградской консерватории, преподавал и сочинял музыку в Харькове и в Ленинграде, а в 1928 году эмигрировал в США и стал там профессором математики и композиции в самых разных учебных заведениях, в том числе и в Колумбийском и в Нью-Йоркском университетах. В числе учеников Шиллингера были знаменитый композитор и пианист Джордж Гершвин, джазовый кларнетист Бенни Гудмен и руководитель свингового оркестра Гленн Миллер. Шиллингер был убежденным приверженцем музыки на математической основе и разработал систему музыкальной композиции, носящую его имя. В частности, в некоторых пьесах последовательность нот в мелодии соответствовала числам Фибоначчи – если считать интервалы по полутонам (рис. 90). По мнению Шиллингера, эти «скачки Фибоначчи» вызывали у слушателя то же ощущение гармонии, что и филлотактическое расположение листьев на стебле – у ботаника. В своей книге «Иосиф Шиллингер. Воспоминания» (Frances Schillinger. Joseph Schillinger: A Memoir) вдова Шиллингера Фрэнсис рассказывает, как однажды композитор в компании друзей ехал в машине в ливень и заметил: «И шум дождя, и дворники, смахивающие воду с лобового стекла, обладают собственным ритмическим рисунком. Это и есть бессознательное искусство». Шиллингер постоянно пытался доказать, что можно основывать музыкальную композицию исключительно на математических формулах, и одна такая попытка привела к интересному результату: Шиллингер скопировал график колебаний фондового рынка из газеты «Нью-Йорк Таймс», переложил его взлеты и падения в пропорциональные музыкальные интервалы и показал, что таким образом получается мелодия, несколько напоминающая сочинения великого Баха.
Вывод из этого краткого экскурса в мир музыки таков: мнение о том, что некоторые композиторы применяли в своих сочинениях золотое сечение, как правило, предполагает чересчур поспешный переход от чисел, получаемых простым подсчетом (количество нот, тактов и пр.) к интерпретации. Тем не менее нет никаких сомнений, что именно в ХХ веке интерес к численной стороне музыки вспыхнул с новой силой. Это возрождение пифагорейского учения, в частности, привело к тому, что и золотое сечение сыграло достаточно важную роль в сочинениях некоторых композиторов.
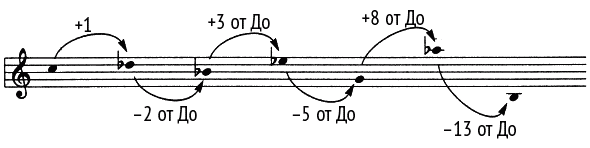
Рис. 90
Весьма красноречиво выразил отношения между музыкой и математикой в своей книге «Прекрасное в музыке» (Eduard Hanslick. The Beautiful in Music) венский музыкальный критик Эдуард Ганслик (1825–1904):
«Музыка» природы и музыка как творение человека принадлежат к двум разным категориям. Переход из первой во вторую происходит средствами математической науки. Это очень важный довод, из которого многое следует. Однако мы бы заблуждались, если бы сделали вывод, будто человек строит свою музыкальную систему согласно осознанным вычислениям, ведь хотя эта система возникла благодаря бессознательному применению заложенных в человеке представлений о количестве и соразмерности посредством тонких процессов расчета и измерения, однако законы, управляющие этими процессами, наука описывает лишь задним числом.

