Равноправие поэтов и живописцев

Живопись – не эстетическая операция, это своего рода магия, предназначенная служить посредником между нами и этим чуждым, враждебным миром.

Пабло Пикассо (1881–1973)

В эпоху Возрождения история золотого сечения потекла по совершенно новому руслу. Эта концепция перестала быть чисто математической. Теперь золотое сечение проложило себе путь в исследования природных явлений и в мир искусства.

Мы уже сталкивались с заявлениями, что архитектурные проекты различных сооружений древности, будь то великая пирамида Хеопса или Парфенон, основаны на золотом сечении. Однако при более пристальном разборе этих заявлений оказывается, что в большинстве случаев они бездоказательны. Представление о «божественной пропорции» и понимание, что без математики невозможно выстроить перспективу, позволили многим художникам примириться с тем, что теперь им придется применять в работе научные методы вообще и золотое сечение в частности. Современный график и живописец Дэвид Хокни в своей книге «Тайное знание» утверждает, к примеру, что начиная примерно с 1430 года, художники начали тайно от всех применять оптические устройства – всевозможные линзы, вогнутые зеркала и camera obscura, дабы придавать правдоподобия своим творениям. Однако применяли ли они золотое сечение? И если да, ограничивалось ли применение золотого сечения изобразительным искусством или же оно проникло и в другие области художественного творчества?

Тайная геометрия для художника

Многие претензии на применение золотого сечения в живописи прямо связаны с тем, что золотому прямоугольнику приписывают особые эстетические свойства. Подлинность (и мнимость) этого эстетического канона мы обсудим чуть дальше. А сейчас мне хотелось бы ненадолго остановиться на гораздо более простом вопросе: действительно ли художники Проторенессанса и эпохи Возрождения основывали композиции своих работ на золотом прямоугольнике? Попытка ответить на этот вопрос заставит нас вернуться в XIII век.

«Мадонна Оньиссанти», известная также как «Мадонна во славе» (рис. 70, хранится в Галерее Уффици во Флоренции) – одна из величайших алтарных картин кисти великого итальянского живописца и зодчего Джотто ди Бондоне (1267–1337). Картина выполнена между 1306 и 1310 годом и изображает Деву Марию, с полуулыбкой восседающую на престоле и нежно поглаживающую колено Младенца Христа. Мадонна с Младенцем окружены святыми и ангелами, расположенными в своего рода «иерархической перспективе». Во многих книгах и статьях о золотом сечении на все лады повторяется утверждение, что будто бы картина в целом и центральные фигуры точно вписываются в золотые прямоугольники (рис. 71).

Рис. 70

Рис. 71

Нечто подобное утверждают и по поводу двух других картин на тот же сюжет: это «Мадонна Ручеллаи» великого сиенского живописца Дуччо ди Буонисенья (иногда его зовут просто Дуччо, ок. 1255–1319), и «Мадонна Санта Тринита» Ченни ди Пепо, известного как Чимабуэ (ок. 1240–1302). Волею судьбы сегодня все три картины висят в одном и том же зале Галереи Уффици во Флоренции. Параметры Мадонн «Оньиссанти», «Ручеллаи» и «Санта Тринита» дают соотношение высоты и ширины в 1,59, 1,55 и 1,73 соответственно. Все эти числа и вправду не очень далеки от золотого сечения, однако два из них ближе к рациональному числу 1,6, чем к иррациональному числу φ. Если это о чем-то и говорит, то лишь о том, что художники руководствовались советом Витрувия и выбирали простые пропорции, соотношение двух целых чисел, а не золотое сечение. Внутренний прямоугольник «Мадонны Оньиссанти» (рис. 71) оставляет столь же неоднозначное впечатление. Границы прямоугольника на иллюстрациях к книгам – например, к прелестной книге Труди Хэммел Гарланд «Чудесные числа Фибоначчи» (Trudi Hammel Garland. Fascinating Fibonaccis) – обычно проводят очень жирными линями, отчего любые измерения становятся весьма неопределенными, но тут и верхняя горизонтальная линия проведена, прямо скажем, произвольно. Мы помним, как опасно полагаться на одни лишь измерения, поэтому вправе задаться вопросом, есть ли другие основания заподозрить, что эти художники сознательно учитывали при создании своих картин золотое сечение. Ответ на этот вопрос, судя по всему, отрицательный – разве что к этому соотношению мастеров влекло некое подсознательное эстетическое чутье (о вероятности такого поворота событий мы еще поговорим). Вспомним, что все три Мадонны были написаны более чем за два столетия до публикации трактата «О божественной пропорции», который привлек к золотому сечению более широкое внимание.

Французский художник и писатель Шарль Було в своей книге «Тайная геометрия художника, вышедшей в 1963 году (Charles Bouleau. The Painter’s Secret Geometry) придерживается иной точки зрения. Он не приводит в пример конкретные картины Джотто, Дуччо и Чимабуэ, однако пишет, что книга Пачоли знаменует не начало новой эпохи, а конец старой. Було утверждает, что трактат «О божественной пропорции» «свидетельствует об идеях, которые долгие столетия передавались исключительно в устной традиции», когда золотое сечение «считалось выражением совершенной красоты». Будь все действительно так, Чимабуэ, Дуччо и Джотто и в самом деле могли бы сознательно применить общепризнанный стандарт совершенства. К сожалению, я не нашел никаких подтверждений гипотезы Було. Напротив, задокументированная история золотого сечения отнюдь не свидетельствует, что в течение столетий, предшествующих публикации трактата Пачоли, художники питали к этому соотношению какое-то особое уважение. Более того, серьезные специалисты, исследовавшие творчество трех вышеупомянутых художников (см. книги «Джотто» Франчески Флорес Д’Арсэ и «Чимабуэ» Лучано Беллози (Francesca Flores D’Arcais. Giotto; Luciano Bellosi. Cimabue)), ни разу не упоминают, что эти художники могли применять золотое сечение: подобные заявления встречаются только в сочинениях энтузиастов золотого сечения и основаны исключительно на сомнительных доказательствах вроде измерений.

Практически все, кто заявляет о появлении золотого сечения в изобразительном искусстве, упоминают и еще одно имя – Леонардо да Винчи. Некоторые авторы даже приписывают Леонардо изобретение термина «божественная пропорция». Обычно разговоры ведутся вокруг пяти произведений итальянского мастера: это неоконченная картина «Св. Иероним», два варианта «Мадонны в скалах», набросок «Голова старика» и прославленная «Джоконда». О «Джоконде» я здесь говорить не буду по двум причинам: во-первых, эта картина и так уже стала предметом бесчисленного множества пространных спекуляций, как научных, так и популярных, посвященных вопросам, на которые в принципе невозможно дать однозначный ответ, во-вторых, золотое сечение ищут в параметрах прямоугольника, описанного вокруг лица Моны Лизы. В отсутствие каких бы то ни было ясных (и задокументированных) указаний, где именно следует чертить этот прямоугольник, подобная идея подает лишь очередной повод для подтасовки цифр. Однако я еще вернусь к более общей теме пропорций лиц у Леонардо, когда мы будем обсуждать «Голову старика».

Случай с двумя вариантами «Мадонны в скалах» (один хранится в Лувре, в Париже, рис. 72, а второй – в Национальной галерее в Лондоне, рис. 73). Отношение высоты к ширине у картины, которая, как полагают, была написана раньше, примерно 1,64, а у более поздней – 1,58; обе эти величины относительно близки к φ, однако близки и к простому соотношению 1,6.

Рис. 72

Рис. 73

Датировка и подлинность двух «Мадонн в скалах» также придают интересный поворот заявлениям о присутствии в их параметрах золотого сечения. Специалисты, изучавшие эти две картины, пришли к выводу, что луврская версия, вне всяких сомнений, была создана рукой самого Леонардо, а версия, хранящаяся в Национальной галерее, вероятно, представляет собой результат совместного труда и по-прежнему вызывает споры. Считают, что луврская версия – это одна из первых работ, которые Леонардо написал в Милане, вероятно, между 1483 и 1485 годами. Вариант из Национальной галереи, с другой стороны, по мнению большинства, был завершен около 1506 года. Эти даты важны для нас по той причине, что с Пачоли Леонардо познакомился в 1496 году при Миланском дворе. Семьдесят первая глава трактата «О божественной гармонии» (конец первой части книги), по словам Пачоли, «была завешена сегодня, 14 декабря, в Милане, в нашем тихом монастыре». Следовательно, первая версия (та, в подлинности которой нет никаких сомнений) была завершена примерно за десять лет до того, как Леонардо получил возможность из первых рук узнать о «божественной пропорции». Утверждение, что Леонардо будто бы применял золотое сечение в «Мадонне в скалах», следовательно, сводится к убеждению, что художник будто бы получил представление об этой пропорции и начал ее применять еще до начала сотрудничества с Пачоли. Не то чтобы это было невозможно, однако такая интерпретация ничем не подтверждается.

Оба варианта «Мадонны в скалах» – бесспорные шедевры Леонардо. Пожалуй, ни в одной другой картине он не нашел лучшего воплощения своему художественному принципу: «Каждое непрозрачное тело окружено и окутано по всей поверхности светом и тенью». Фигуры на картинах буквально распахнуты к зрителю, вовлекают его в эмоциональное общение. Утверждать, будто эти картины хотя бы отчасти обязаны силой воздействия простому соотношению частей, без нужды принижает и упрощает гений Леонардо. Давайте не будем обманываться: благоговение, которое охватывает нас при виде «Мадонны в скалах», не имеет практически никакого отношения к тому, применялось ли золотое сечение в композиции картин.

С той же неопределенностью можно судить и о незаконченном «Святом Иерониме» (рис. 74, хранится в музеях Ватикана). Дело не только в том, что картина датируется 1483 годом – то есть написана задолго до переезда Пачоли в Милан: утверждение, которое можно найти в некоторых книгах и статьях (например, у Давида Бергамини (David Bergamini) и редакторов тома «Математика» в серии научно-популярных книг журнала «Life»), что Святой Иероним будто бы точно вписывается в золотой прямоугольник, весьма и весьма натянуто. На самом деле стороны прямоугольника не касаются контуров фигуры, особенно слева, и проходят совсем далеко от головы, зато рука выдается далеко за пределы прямоугольника.

Последний пример гипотетического применения золотого сечения на картинах Леонардо – «Голова старика» (рис. 75, рисунок хранится в Галерее Академии в Венеции). Профиль и схема пропорций нарисованы пером около 1490 года. Около 1530–1504 годов на том же листе были сделаны два наброска всадников сангиной – полагают, что это этюды к фреске «Битва при Ангиари».

Рис. 74

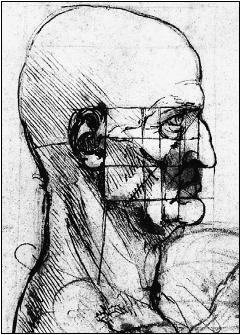
Рис. 75

Сеть вспомогательных линий, конечно, не оставляет сомнений, что Леонардо всерьез интересовался пропорциями лица, однако сделать из этого наброска какие-либо определенные выводы очень трудно. Например, прямоугольник слева вверху – это более или менее золотой прямоугольник, однако линии начерчены так небрежно, что мы не можем ничего утверждать с уверенностью. Тем не менее, этот рисунок, пожалуй, ближе всего подводит к доказательству, что Леонардо и правда определял параметры своих картин при помощи прямоугольников и даже, вероятно, подумывал о том, не применить ли в своем творчестве золотое сечение.

Интерес Леонардо к пропорциям лица, возможно, нашел и другое, не менее любопытное проявление. В статье, напечатанной в «Scientific American» в 1995 году, историк искусства и графический дизайнер Лилиан Шварц рассказала об интересном наблюдении. По мнению Шварц, в отсутствии модели для «Джоконды» Леонардо придал портрету некоторые собственные черты. Предположение Шварц основано на компьютерном сравнении различных параметров лица Моны Лизы и соответствующих черт на портрете сангиной, который, по убеждению большинства исследователей (если даже не по единодушному их мнению) считается единственным автопортретом Леонардо. Однако, как указывали другие искусствоведы, подобие пропорций, вероятно, свидетельствует лишь о том, что при создании этих портретов Леонардо пользовался одними и теми же формулами пропорций (входило в них золотое сечение или нет, неизвестно). Да и сама Шварц отмечает, что те же пропорции, что и на рисунке «Головы старика», Леонардо применяет даже на гротесковых рисунках – серии уродливых лиц с карикатурно увеличенными подбородками, ртами, носами и лбами.

Однако если есть сильные сомнения в том, что сам Леонардо, не просто личный друг Пачоли, но и иллюстратор его трактата «О божественной пропорции», применял золотое сечение в композиции своих работ, значит ли это, золотое сечение не мог применить кто-то другой? Конечно, не значит. В конце XIX века появилось огромное множество ученых трудов, посвященных золотому сечению, и художники, само собой, стали обращать внимание на это понятие. Но прежде чем мы поговорим о художниках, которые и в самом деле опирались на золотое сечение, необходимо развенчать еще один миф.

Несмотря на многочисленные заявления об обратном, французский пуантилист Жорж Сёра (1859–1891), вероятно, не применял золотое сечение в своих работах. Сёра интересовался цветовосприятием и сочетаниями цветов и при помощи особой техники – пуантилизма, или множества разноцветных точек – пытался передать переливчатость, мерцание света. В последние годы жизни он также интересовался художественными средствами передачи различных чувств. В письме, написанном в 1890 году, Сёра вкратце перечисляет некоторые свои воззрения.

Искусство есть гармония. Гармония есть сопоставление подобного и противоположного в тоне, светотени, линии, выбранных по принципу и под влиянием игры света в сценах веселых, легких, печальных. Противоречия – это… в том, что касается линий – прямой угол… веселые линии – линии над горизонталью… спокойствие – горизонталь, печальные линии направлены вниз.

Все эти идеи Сёра выразил в своем полотне «Цирковой парад» (рис. 76, хранится в музее Метрополитен в Нью-Йорке). Обратите особое внимание на прямой угол между балюстрадой и вертикальной линией справа посередине полотна. Вся композиция основана на принципах, которые Сёра почерпнул в книге теоретика-искусствоведа Давида Саттера «Философия изящных искусство применительно к живописи» (David Sutter. La philosophie des Beaux-Arts appliquée а la peinture, 1870). Саттер писал: «Если доминанта горизонтальна, на ней нужно поместить череду вертикальных предметов, поскольку тогда эта последовательность будет конкурировать с горизонтальной линией».

Рис. 76

Страстные поклонники золотого сечения зачастую приводят анализ «Парада» (наряду с другими работами Сёра, в частности, «Цирком»), в «доказательство», что художник сознательно применял φ. Даже в чудесной книге «Математика» Бергамини и редакторов журнала «Life» мы читаем: ««Парад», написанный мелкими точками, в характерной манере французского импрессиониста Жоржа Сёра, содержит множество примеров золотых пропорций». Более того, в книге приводится цитата («по словам одного искусствоведа»), где говорится, что Сёра «к каждому своему холсту подступал с золотым сечением». К сожалению, все эти утверждения безосновательны. Горячим сторонником и распространителем этого мифа был родившийся в Румынии священник и писатель Матила Гика (1881–1965), еще один «искусствовед», которого цитирует Бергамини. Гика опубликовал две авторитетные книги – «Эстетику пропорций в природе и в искусстве» («Esthétique des proportions dans la nature et dans les arts», 1927) и уже упоминавшуюся книгу «Золотое сечение», полное название которой – «Золотое сечение, пифагорейские ритуалы и ритмы в развитии Западной цивилизации» («Le Nombre d’Or: Rites et rythmes pytagoriciens dans le développement de la civilisation occidentale», 1931). Обе книги представляют собой полумистические толкования математических фактов. В них рука об руку с точным описанием математических свойств золотого сечения приводятся анекдотические материалы о появлении золотого сечения в искусстве (Парфенон, египетские пирамиды и прочее). Парадоксально, но факт: эти книги были очень авторитетны.

Что касается самого «Парада», горизонтальная линия на нем и в самом деле разделена в пропорциях, близких к золотому сечению (в действительности, в простом соотношении восемь пятых), однако вертикаль – отнюдь нет. Анализ всей композиции этого и других полотен Сёра, а также работ художника-символиста Пьера Пюви де Шаванна (1824–1898), заставляет даже такого горячего сторонника золотого сечения, как художник и писатель Шарль Було, сделать печальный вывод: «Не думаю, чтобы мы могли без подтасовки данных сказать, что его [Пюви де Шаванна] композиции основаны на золотом сечении. То же самое относится и к Сёра». Подробный анализ всех картин, записей и набросков Сёра, который в 1980 году выполнил Роджер Герц-Фишлер, подводит к тем же выводам. Более того, математик, философ и художественный критик Чарльз Генри (1859–1926) еще в 1890 году твердо заявил, что «современные художники полностью пренебрегают» золотым сечением.

Так кто же тогда применял золотое сечение как в своих картинах, так и в теории живописи? Вероятно, первым выдающимся художником и теоретиком искусства, кто сознательно применял золотое сечение, был Поль Серюзье (1864–1927). Серюзье родился в Париже, некоторое время изучал философию, а затем поступил в прославленную школу искусств «Академия Жюлиана». Знакомство с художниками Полем Гогеном и Эмилем Бернаром заставило его перенять их колорит и символистские воззрения. Вместе с художниками-постимпрессионистами Пьером Боннаром, Эдуаром Вилларом, Морисом Дени и другими он основал группу под названием «Наби», что на древнееврейском значит «пророки». Название объяснялось полусерьезным, полушутовским отношением участников группы к своему новому стилю, который они представляли как своего рода религиозное просветление. С этой группой был связан и композитор Клод Дебюсси. Серюзье, вероятно, впервые услышал о золотом сечении между 1896 и 1903 годами, во время одной из поездок к своему другу, голландскому художнику Яну Веркаде (1868–1946). Веркаде был послушником в бенедиктинском монастыре в городе Бойрон на юге Германии. Там группы художников-монахов исполняли довольно скучные композиции на религиозные темы с соблюдением «священных пропорций» согласно теории отца Дидье Ленца. По гипотезе отца Ленца, все величайшие творения древности (Ноев ковчег, египетские шедевры зодчества и пр.) были основаны на простых геометрических понятиях – окружности, равностороннем треугольнике и правильном шестиугольнике. Эта теория показалась Серюзье чрезвычайно привлекательной, и он писал Веркаде: «Представь себе, [я] много говорил о геометрических параметрах, о которых ты мне рассказывал». Художник Морис Дени (1870–1943) оставил о Серюзье биографические заметки, из которых мы узнаем, что в число «геометрических параметров» отца Ленца входило и золотое сечение. Хотя Серюзье признает, что первоначально изучение математики Бойрона было для него «делом нелегким», идеи о золотом сечении и его предположительной связи с великой пирамидой Хеопса и произведениями древнегреческого зодчества проникла и в важную книгу Серюзье по теории искусств «Азбука живописи» (Paul Sérusier. L’ABC de la Peinture).

Похоже, интерес Серюзье к золотому сечению был скорее философским, чем практическим, однако художник и в самом деле применил это соотношение в композиции некоторых своих работ, в основном с целью «подтвердить, а иногда просто проверить свои изобретения в области формы и композиции».

Серюзье проложил концепции золотого сечения путь и в другие художественные объединения, в основном – в среду кубистов. Термин «кубизм» придумал художественный критик Луи Восель (которому мы, кстати, обязаны и словами «фовизм» и «экспрессионизм») после выставки Жоржа Брака в 1908 году. Официальное начало этому движению положили картины «Авиньонские девицы» Пикассо и «Большая обнаженная» Брака. Пикассо и Брак восстали против страстного колорита и неуемных форм экспрессионизма и разработали свой строгий, практически монохромный стиль, сознательно отказавшись от любой тематики, которая могла бы вызвать эмоциональные ассоциации. Предметы вроде музыкальных инструментов и даже человеческие тела разделялись на многогранные геометрические фигуры, которые затем комбинировались, причем перспектива постоянно менялась. Применение геометрических понятий вроде золотого сечения очень подходило для такого анализа формы тел, целью которого было обнажить их структуру. И в самом деле, первые кубисты, в том числе Жак Вийон и его братья Марсель Дюшан и Раймон Дюшан-Вийон, а также Альбер Глез и Франсис Пикабиа в октябре 1912 года организовали в Париже целую выставку, которая так и называлась «Золотое сечение» («Section d’Or»). Несмотря на крайне многообещающее название, золотого сечения не было в композиции ни одной из выставленных картин. Организаторы выбрали этот термин лишь ради того, чтобы подчеркнуть свой интерес к вопросам связи искусства с наукой и философией. Тем не менее некоторые кубисты, в том числе художник испанского происхождения Хуан Грис (1887–1927) и родившийся в Литве скульптор Жак (Хаим-Яков) Липшиц (1891–1973) и в самом деле руководствовались золотым сечением в некоторых поздних работах. Липшиц писал: «В то время я очень интересовался теориями математических пропорций, как и прочие кубисты, и пытался применить их в своих скульптурах. Всех нас очень занимала идея золотого правила или золотого сечения – считалось, что эта система заложена во всем искусстве и архитектуре Древней Греции». Липшиц помогал Хуану Грису при создании скульптуры «Арлекин» (Художественный музей Филадельфии, рис. 77) – для достижения желаемых пропорций художники применили треугольник Кеплера (основанный на золотом сечении, см. рис. 61).

Рис. 77

В начале 1920 годов золотое сечение применял еще один художник – итальянский живописец Джино Северини (1883–1966). В своей работе Северини пытался примирить несколько противоречивые цели футуризма и кубизма. Футуризм отражал стремление группы итальянских мыслителей, работавших в области литературы, изобразительного искусства, театра, музыки и кинематографа, способствовать обновлению итальянской культуры. По словам самого Северини: «Мы решили сосредоточить внимание на предметах в движении, поскольку современный тип чувствительности особенно предрасположен к тому, чтобы ухватить идею скорости». Первый манифест художников-футуристов был подписан в 1910 году и всячески побуждал молодых итальянских художников «глубоко презирать всевозможную имитацию». Оставаясь футуристом, Северини обрел в кубизме «идею меры», которая соответствовала его честолюбивому стремлению «живописными средствами создать объект, столь же совершенный с точки зрения мастерства, что и великолепный буфет работы краснодеревщика». Такое стремление к геометрическому совершенству заставило Северини применять золотое сечение в подготовительных эскизах к нескольким работам (см. «Материнство», сейчас хранится в частной коллекции в Риме, рис. 78). Интересный пример роли золотого сечения в кубистическом искусстве – творчество русской художницы-кубистки Марии Воробьевой, известной как Маревна (1892–1984). В 1974 году Маревна написала книгу «Моя жизнь с художниками “Улья”», где очень увлекательно рассказывает о жизни и работе своих друзей – группы, куда входили художники Пикассо, Модильяни, Сутин, Ривера (от которого у Маревны родилась дочь) и другие – в Париже в двадцатые годы. Хотя Маревна не приводит никаких конкретных примеров, а ее исторические замечания зачастую неточны, из текста следует, что Пикассо, Ривера и Грис применяли золотое сечение как очередной, более сложный способ делить плоскость, предназначенный для знатоков и ценителей.

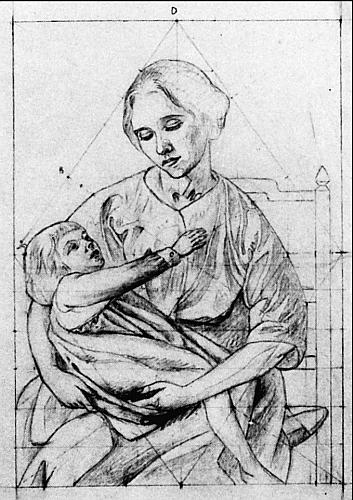
Рис. 78

В начале ХХ века золотым сечением очень интересовался и американский искусствовед Джей Хембридж (1867–1924). Хембридж выпустил целый ряд статей и книг, где определял два типа симметрии в классическом и современном искусстве. Первый он назвал статической симметрией, и такая симметрия основана на правильных фигурах наподобие квадрата и равностороннего треугольника и, по мнению исследователя, приводила к созданию безжизненных произведений искусства. В создании другой симметрии, которую он назвал динамической, главную роль играли золотое сечение и логарифмическая спираль. Главный тезис Хембриджа состоял в том, что применение динамической симметрии в композиции приводит к созданию живых и трогательных произведений искусства. Сегодня лишь немногие воспринимают его идеи всерьез.

Одним из самых ярых сторонников применения золотого сечения в искусстве и архитектуре был знаменитый швейцарско-французский архитектор и художник Ле Корбюзье (Шарль-Эдуар Жаннере-Гри, 1887–1965). Жаннере родился в Ла-Шо-Де-Фон в Швейцарии, где учился живописи и гравюре. Отец его работал эмальером в часовой мастерской, а мать была пианисткой и учительницей музыкой и, помимо более абстрактных занятий, всячески склоняла сына стать музыкантом-виртуозом… В 1905 году Жаннере стал изучать архитектуру и впоследствии стал одной из самых влиятельных фигур в современной архитектуре. Зимой 1916–1917 года Жаннере переехал в Париж и познакомился там с Амеде Озанфаном, который был вхож в высшее парижское общество художников и мыслителей. Благодаря Озанфану Жаннере познакомился с кубистами и невольно перенял их эстетические взгляды. В частности, Хуан Грис заразил его интересом к системам пропорций и их роли в эстетике. Осенью 1918 года Жаннере и Озанфан устроили совместную выставку в галерее Тома. Точнее, две картины Жаннере соседствовали с куда более многочисленными полотнами Озанфана. Озанфан и Жаннере назвали себя пуристами, а каталог своей выставки озаглавили «Après le Cubisme» – «После кубизма». Пуризм возрождает идеи Пьеро делла Франческа и платоновской эстетической теории: он утверждает, что «произведение искусства не должно быть случайным, исключительным, импрессионистским, неорганичным, протестным, картинным – напротив, оно должно быть обобщенным, статичным, выразительным за счет постоянства».

Псевдоним Ле Корбюзье (позаимствованный у предков с материнской стороны, чья фамилия была Лекорбезье) Жаннере взял лишь в 33 года, когда он уже пустил корни в Париже и был уверен в своем будущем. Судя по всему, он в целом хотел перечеркнуть мелкие неудачи прошлого и создать миф о том, что его архитектурный гений расцвел в одночасье. Поначалу Ле Корбюзье относился к применению золотого сечения в искусстве довольно-таки скептически и даже отрицательно – он предостерегал против того, чтобы «замещать здравый смысл мистицизмом при помощи золотого сечения». Более того, подробный анализ архитектурных проектов и «пуристских» работ Ле Корбюзье, который проделал Роджер Герц-Фишлер, показывает, что до 1927 года Ле Корбюзье ни разу не применял золотое сечение. Ситуация резко переменилась после выхода в свет уже упоминавшегося авторитетного труда Матилы Гика «Эстетика пропорций в природе и искусстве», а с появлением в 1931 году его «Золотого сечения» мистические аспекты φ стали волновать читающую публику еще сильнее. Ле Корбюзье увлекся «Эстетикой» и золотым сечением по двум причинам. С одной стороны, это было следствием его интереса к основным геометрическим формам и структурам, скрытым за природными явлениями. С другой стороны, в семье Ле Корбюзье приветствовали музыкальное образование, и он вполне мог оценить пифагорейское стремление к гармонии, достигаемой соотношениями чисел. Он писал: «Более тридцати лет назад по жилам моих работ – и архитектурных, и живописных – заструился сок математики, ибо музыка никогда меня не покидает». Поиски стандартизированной пропорции достигли пика в создании новой системы пропорций – Модулера.

Предполагалось, что Модулер станет «гармонической мерой человеческого масштаба, применимой универсально в архитектуре и в механике». В сущности, такое определение – не более чем перефразированное знаменитое изречение Протагора, высказанное в V веке до н. э.: «Человек есть мера всех вещей». Естественно, Модулер был основан на пропорциях человеческого тела (рис. 79) – в духе «Витрувианского человека» (рис. 53) и общей философской задачи создать систему пропорций, эквивалентной той, что создала природа. Человек ростом шесть футов (около 183 см), несколько напоминающий знакомого «мишленовского человечка» с рекламы шин, с поднятой рукой (общая высота составляет 226 см, или 7 футов 5 дюймов), вписан в квадрат (рис. 80). Отношение его роста (183 см, 6 футов) к расстоянию от подошв до пупка (на середине общей высоты – 113 см, 3 фута 8,5 дюймов) – это в точности золотое сечение. Общая высота – от подошв до кончиков пальцев поднятой руки – также делится в золотом сечении (на 140 см и 86 см) на уровне запястья опущенной руки. Два отношения – 113/70 и 140/86 – подразделялись далее на более мелкие величины в соответствии с последовательностью Фибоначчи – каждое число есть сумма двух предыдущих (рис. 81). Окончательная версия Модулера (рис. 79 и 81), таким образом, опиралась на две взаимопроникающие шкалы чисел Фибоначчи («красная и голубая серии»). По предложению Ле Корбюзье Модулер должен был обеспечить гармонические пропорции всему – от размеров дверных ручек и шкафов до зданий и городов. В мире, где постоянно росла потребность в массовом производстве, Модулер должен был предоставить модель для стандартизации. Ле Корбюзье выпустил две книги – «Модулер» (1948) и «Модулер II» (1955) (Le Corbusier. Le Modulor; Le Corbusier. Modulor II), которые вызвали пристальное внимание в кругах специалистов по архитектуре и до сих пор служат аргументом в любом споре о пропорциях. Ле Корбюзье очень гордился тем, что ему представился случай показать «Модулер» самому Альберту Эйнштейну – они встречались в Принстоне в 1946 году. Вот как архитектор вспоминал этот момент: «Я плохо говорил, плохо рассказал о Модулере, завяз в трясине причинно-следственных связей». Тем не менее, Эйнштейн написал ему письмо, где сказал о Модулере так: «Это шкала пропорций, благодаря которой сделать плохо станет трудно, а сделать хорошо – легко».

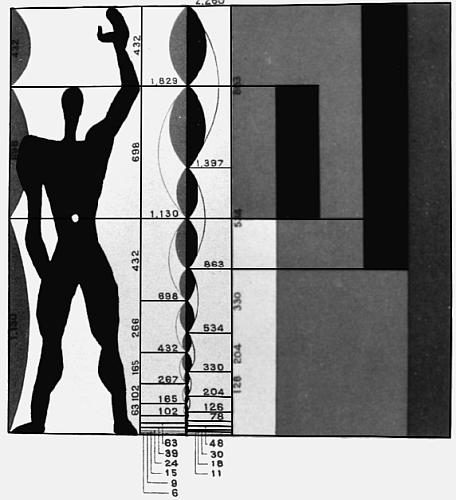
Рис. 79

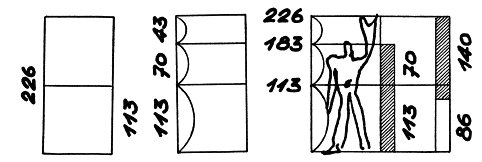
Рис. 80

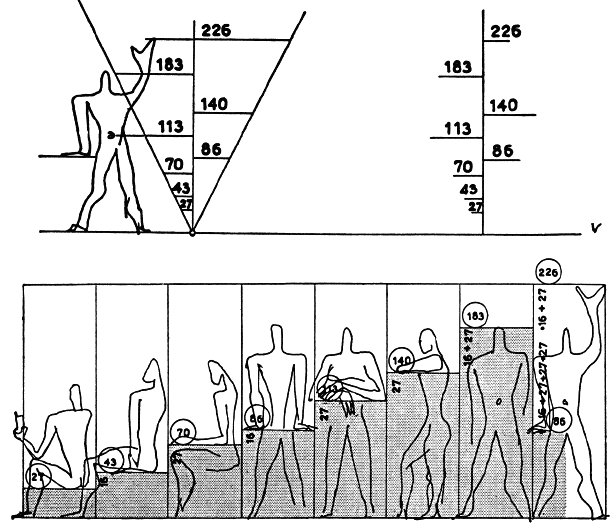
Рис. 81

Свою теорию Модулера Ле Корбюзье воплощал на практике во многих своих проектах. Скажем, в предварительных заметках к проекту целого индийского города Чандигарх, где стоят четыре крупных правительственных здания – парламент, дворец правосудия и два музея – мы читаем: «Однако, разумеется, при разработке ритма окон учитывается Модулер… в общей части здания, где, в частности, многочисленные кабинеты и залы суда должны укрываться от солнца, Модулер обеспечивает единство текстуры. В дизайне фасадов Модулер (с точки зрения текстуры) задействует красную и голубую серию в пределах пространств, уже ограниченных оконными рамами».

Разумеется, художники интересовались золотым сечением и после Ле Корбюзье, однако большинство его последователей увлекались скорее математико-философски-историческими качествами этого соотношения, нежели его предполагаемыми эстетическими свойствами. Скажем, английский абстракционист Энтони Хилл в 1960 году применил последовательность Фибоначчи в параметрах своей работы «Конструктивный рельеф» (рис. 82). Подобным же образом современный израильский художник и скульптор Игаль Тумаркин сознательно включил формулу φ (φ = (1+√5)/2) в одну из своих картин.

Рис. 82

Итальянец Марио Мерц превратил последовательность Фибоначчи в важную составляющую своих работ. Мерц родился в Милане в 1925 году, а в 1967 году примкнул к художественному течению «Арте повера» (итал. «Arte Povera» – «бедное искусство»), куда также входили художники Микеланджело Пистолетто, Лучано Фабро и Яннис Кунеллис. Название движения (его придумал критик Джермано Челант) объясняется стремлением участников применять в своем творчестве простые повседневные материалы в знак протеста против негуманного общества потребления, каким они его видели. Применять последовательность Фибоначчи Мерц начал в 1970 году в серии «концептуальных» работ, куда входили последовательности чисел и разнообразные спирали.

Мерц так стремился применять числа Фибоначчи, поскольку эта последовательность лежит в основе многих закономерностей роста и развития в природе. В своей работе 1987 года под названием «Ударная волна» («Onda d’urto») художник разместил длинный ряд стопок газет, над каждой из которых сияют неоновые числа Фибоначчи. Работа «Неаполь Фибоначчи» (1970) состоит из 10 фотографий фабричных рабочих, где количество изображенных возрастает в соответствии с последовательностью Фибоначчи от одиночных портретов до группы из 55 человек (десятое число Фибоначчи).

Необоснованные утверждения, что тот или иной художник якобы применял в своем творчестве золотое сечение, множатся, словно грибы после дождя. Одно подобное заявление заслуживает особого разбора, поскольку его без конца повторяют. Голландский художник Пит Мондриан (1872–1944) известен в основном благодаря своему беспредметному геометрическому стилю, который он назвал неопластицизмом. В частности, для композиции многих его картин характерно применение исключительно вертикальных и горизонтальных линий, прямоугольников и квадратов и только основных цветов (иногда – с вкраплениями черного и серого) на белом фоне, как, например, в картине «Буги-вуги на Бродвее» (рис. 83, хранится в Музее современного искусства в Нью-Йорке). Изогнутые линии, трехмерность, реалистичность изображения в его творчестве полностью исключались.

Рис. 83

Наверное, не стоит удивляться, что геометрические композиции Мондриана привлекли пристальное внимание адептов золотого сечения и стали предметом различных спекуляций. Дэвид Бергамини в своей «Математике» признает, что сам Мондриан «толковал композицию своих картин расплывчато», но тем не менее, утверждает, что линейная абстракция «Площадь Согласия» заключает в себе взаимоперекрывающиеся золотые прямоугольники. Шарль Було в своей «Тайной геометрии художника» позволяет себе еще более смелые заявления: он утверждает, что «Французские художники никогда не осмеливались заходить так далеко в чистую геометрию и так строго и последовательно применять золотое сечение, как холодный и безжалостный голландец Пит Мондриан». Далее Було говорит, что в «Буги-вуги на Бродвее» «почти все горизонтали и вертикали, составляющие картину, построены на золотом сечении». Я потратил некоторое время на изучение более серьезных работ о творчестве Мондриана и не нашел там ни единого упоминания о золотом сечении, и тогда мне стало интересно, как же все было на самом деле: применял или не применял Мондриан золотое сечение в композиции своих картин? В отчаянии я решил прибегнуть к последнему средству и обратился к настоящему специалисту. Это был Ив-Ален Буа из Гарвардского университета, соавтор книги «Мондриан» (Yves-Alain Bois et al. Mondrian), выпущенной в 1999 году к ретроспективной выставке художника. Ответ Буа был совершенно недвусмыслен: «Насколько мне известно, у Мондриана никогда не было никакой системы пропорций, если не считать своего рода сеток из модулей, которые он писал в 1918–1919 годах, но там система выводилась из формата самих картин – восемь на восемь единиц». Далее Буа добавил: «Помнится, и сам Мондриан язвил по поводу того, что в его работах якобы использовались арифметические выкладки». «Думаю, что золотое сечение применительно к Мондриану – чистой воды чушь». Все эти занимательные исторические анекдоты оставляют один нерешенный вопрос. По какой же причине столь много художников задумывались о том, как задействовать золотое сечение в композиции своих работ – если не считать чисто интеллектуального любопытства? Может быть, это соотношение, выраженное в виде золотого прямоугольника, и в самом деле обладает какими-то имманентными эстетическими свойствами, которые ставят его выше других пропорций? Сами по себе попытки ответить на этот вопрос привели к массе психологических экспериментов и написанию множества книг и статей.