Mysterium Cosmographicum
Иоганна Кеплера помнят в основном как выдающегося астронома, оставившего нам, помимо всего прочего, три закона движения планет, носящие его имя. Однако Кеплер был также и талантливым математиком, тонким метафизиком и плодовитым писателем. Родился он во времена больших политических потрясений и религиозных войн, которые коренным образом повлияли и на его образование, и на жизнь, и на мышление. Кеплер родился 27 декабря 1571 года в Германии, в имперском городе Вайль-дер-Штадт, в доме своего деда Зебальда. Отец Иоганна Генрих, наемный солдат, почти все детские годы сына провел в походах, а во время кратких побывок, по словам Кеплера, вел себя «оскорбительно, резко и задиристо». Когда Кеплеру было около шестнадцати, отец ушел из дома, и больше его не видели. Видимо, он участвовал в каком-то морском походе в составе флота Неаполитанского королевства и умер по дороге домой. Следовательно, воспитывала Кеплера в основном его мать Катарина, работавшая в гостинице, которую держал ее отец. Сама Катарина была женщина со странностями, довольно-таки неприятная, собирала травы и была убеждена в их волшебных целительных свойствах. Стечение обстоятельств – личные обиды, неудачные сплетни и алчность – в конечном счете привело к тому, что Катарина уже в старости, в 1620 году, была арестована по обвинению в ведовстве. В то время подобные обвинения были нередки, в период с 1615 по 1629 год в Вайль-дер-Штадте казнили за колдовство как минимум 38 женщин. Кеплер на момент ареста матери был уже известным человеком, и весть о суде над матерью вызвала у него «несказанное огорчение». В сущности, он взял на себя ее защиту в суде и заручился помощью юридического факультета Тюбингенского университета. Процесс был долгим, но в конце концов обвинение с Катарины Кеплер было снято, в основном благодаря ее собственным показаниям, данным под угрозой страшных пыток: Катарина упорно отрицала свою вину. Эта история передает атмосферу, в которой проходила научная работа Кеплера, и доминирующие в то время умонастроения. Кеплер родился в обществе, всего за полвека до этого пережившем отход Мартина Лютера от католической церкви и его заявление, что единственное, что нужно Господу от человека – это вера. Этому обществу еще предстояло погрузиться в кровавое безумие Тридцатилетней войны. Можно лишь изумляться, как Кеплер, человек из подобной среды, на долю которого выпали такие взлеты и падения, столь бурная жизнь, сумел сделать открытие, которое многие считают подлинным рождением современной науки.
Научные изыскания Кеплер начал еще в школе при монастыре Маульбронн, а затем, в 1589 году, выиграл стипендию герцога Вюртембергского и получил возможность посещать лютеранскую семинарию при Тюбингенском университете. Больше всего его интересовали две темы, теология и математика; в его представлении они были теснейшим образом связаны. Астрономию в то время считали частью математики, и наставником Кеплера в астрономии был выдающийся ученый Михаэль Местлин (1550–1631); связь с ним Кеплер поддерживал и после отъезда из Тюбингена. Во время официальных занятий Местлин, конечно, учил лишь традиционной птолемеевой, геоцентрической системе, согласно которой Луна, Меркурий, Венера, Солнце, Марс, Юпитер и Сатурн вращаются вокруг стационарной Земли. Однако Местлин был прекрасно осведомлен о гелиоцентрической системе Николая Коперника, сведения о которой были опубликованы в 1543 году, и в частных беседах обсуждал со своим любимым учеником Кеплером достоинства этой системы. По системе Коперника шесть планет (включая Землю, однако исключая Луну, которая считалась уже не планетой, а «спутником») вращаются вокруг Солнца. Примерно так же, как из движущегося автомобиля можно наблюдать лишь относительное движение других машин, в системе Коперника движение планет во многом попросту отражает движение самой Земли.
Похоже, система Коперника Кеплеру сразу понравилась. Фундаментальная идея этой космологии, согласно которой центральное Солнце окружено сферой неподвижных звезд, причем между Солнцем и сферой остается некоторое пространство, в точности соответствовала представлению Кеплера о мироздании. Кеплер был человек глубоко религиозный и верил, что Вселенная – отражение Творца. Единство Солнца, звезд и пространства между ними были для него символическим подобием Святой Троицы – Отца, Сына и Святого Духа.
Когда Кеплер с отличием закончил факультет изящных искусств и был уже готов завершить теологическое образование, произошло событие, изменившее его выбор профессии: он стал не пастором, а учителем математики. Протестантская семинария австрийского города Грац попросила Тюбингенский университет порекомендовать заместителя для одного из своих преподавателей математики, который скоропостижно скончался, и университет выбрал Кеплера. В марте 1594 года Кеплер не по своей воле отправился в путешествие в Грац в австрийской провинции Стирия; на дорогу ушел целый месяц.
Поняв, что судьба навязала ему карьеру математика, Кеплер преисполнился решимости исполнить свой христианский долг так, как он его себе представлял: постигнуть творение Господне, устройство Вселенной. Поэтому он проштудировал переводы «Начал» и труды александрийских геометров Аполлония и Паппа. Опираясь на основной принцип коперниковой гелиоцентрической системы, Кеплер решил найти ответы на два главных вопроса: почему планет именно шесть и что определяет именно такие расстояния между планетарными орбитами. Вопросы «почему» и «что» в астрономии были в новинку. В отличие от своих предшественников, которым было довольно всего-навсего отмечать наблюдаемые положения планет, Кеплер стремился вывести теорию, которая бы все объясняла. Свой новый подход, выход на новый уровень любознательности Кеплер объяснял очень красиво:
При любых умственных изысканиях бывает так, что начинаем мы с того, что поражает чувства, а затем благодаря своему устройству разум возносится к вышнему, к тому, чего не постигнуть, сколь бы остры ни были наши чувства. То же самое бывает и в астрономических занятиях, когда мы прежде всего воспринимаем глазами различные положения планет в разное время, а затем в дело вступает логика и на основании этих наблюдений ведет разум к постижению устройства Вселенной.
Однако Кеплер задавался еще одним вопросом: при помощи какого орудия Господь проектировал Свою Вселенную? Первые мысли, которые впоследствии сложились в совершенно фантастические ответы на космические вопросы, посетили Кеплера 19 июля 1595 года, когда он пытался объяснить конъюнкцию внешних планет – Юпитера и Сатурна (положение, при котором у двух небесных тел одни и те же небесные координаты). В общих чертах Кеплер понял вот что: если вписать равносторонний треугольник в окружность (так, чтобы его вершины лежали на окружности), а потом вписать другую окружность в этот треугольник (так, чтобы она касалась середин сторон, см. рис. 58), соотношение радиуса большей окружности к радиусу меньшей будет примерно таким же, как соотношение размеров орбиты Сатурна к размерам орбиты Юпитера. Продолжая рассуждать в том же духе, Кеплер решил, что, дабы получить орбиту Марса (следующей планеты, ближе к Солнцу), нужно вписать в маленький круг следующую геометрическую фигуру, то есть квадрат. Однако при этом нужного размера не получилось. Кеплер не сдался, а поскольку он уже ступил на путь платоновского образа мысли – был убежден, что «Господь геометризирует», – то, естественно, сделал следующий геометрический шаг и обратился к трехмерным телам. В результате этого умственного упражнения Кеплер впервые прибегнул к геометрическим телам, связанным с золотым сечением.
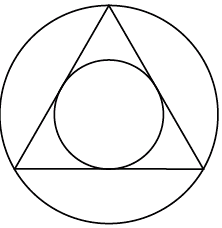
Рис. 58
Ответ на первые два вопроса, которые занимали Кеплера, дан в первом его трактате под названием «Mysterium Cosmographicum» («Космографическая загадка»), который вышел в свет в 1597 году. Полное название, приведенное на титульном листе книги (рис. 59; хотя там стоит дата публикации 1596, вышла книга только в следующем году) гласит: «Предварительное введение в космографические рассуждения, содержащее вселенскую загадку восхитительных пропорций Небесных Сфер, а также Истинные и Подлинные Причины их Размеров, Количества и Периодического Движения Небес, доказанные при помощи Пяти Правильных Геометрических Тел».

Рис. 59
Ответ на вопрос, почему планет именно шесть, дался Кеплеру очень просто: потому что правильных платоновых тел ровно пять. Если считать, что они задают промежутки между планетами, получается шесть промежутков, считая внешнюю сферическую границу – небеса с фиксированными звездами. Более того, модель Кеплера призвана дать ответ и на вопрос о размерах орбит. Вот как пишет сам ученый:
Земная сфера есть мера всех остальных орбит. Опиши вокруг нее додекаэдр. Сфера, его окружающая, будет сферой Марса. Опиши вокруг Марса тетраэдр. Сфера, окружающая его, будет сферой Юпитера. Опиши куб вокруг Юпитера. Окружающая его сфера будет сферой Сатурна. Теперь впиши икосаэдр в орбиту Земли. Вписанная в него сфера будет сферой Венеры. Впиши октаэдр в орбиту Венеры. Сфера, вписанная в него, будет сферой Меркурия. Вот тебе и обоснование количества планет.
На рис. 60 показана схема из «Mysterium Cosmographicum», иллюстрирующая космологическую модель Кеплера. Кеплер довольно пространно объясняет, почему он проводит конкретные параллели между платоновыми телами и планетами на основании их геометрических, астрологических и метафизических свойств. Он расположил геометрические тела на основании их отношения к сфере, предположив, что разница меду сферой и остальными геометрическими телами отражает разницу между творцом и творением. Подобным же образом куб характеризуется одним-единственным углом – прямым. Для Кеплера это символизировало одиночество, которое ассоциируется с Сатурном, и т. д. Вообще говоря, астрология была для Кеплера так важна, поскольку «Человек есть венец Вселенной и всего творения», и метафизический подход обосновывался тем обстоятельством, что «математические свойства – причины физических, поскольку Бог с самого начала времен заключал в себе математические объекты как простые божественные абстракции, служившие прототипами для различных количеств на материальном уровне». Положение Земли было выбрано так, чтобы разделять тела, которые можно поставить стоймя (куб, тетраэдр и додекаэдр), от тел, которые «парят» (октаэдра и икосаэдра).
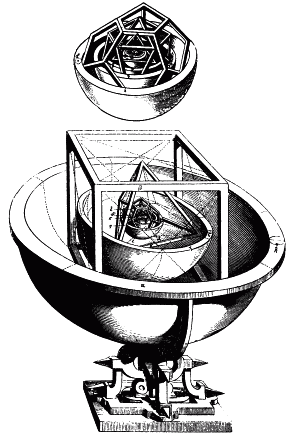
Рис. 60
Расстояния между планетами, полученные из этой модели, в одних случаях вполне совпадали с действительностью, а в других заметно отличались, правда, различие составляло не более 10 %. Кеплер был непоколебимо убежден в правильности своей модели и несоответствия списывал на погрешности измерения орбит. Он разослал экземпляры своей книги различным астрономам, чтобы они высказали свои замечания и предложения; в их числе был и один из самых выдающихся ученых того времени датчанин Тихо Браге (1546–1601). Один экземпляр попал даже в руки великому Галилео Галилею (1564–1642), который сообщил Кеплеру, что тоже уверен в правильности модели Коперника, однако с огорчением признал, что «огромному множеству людей, ибо таково количество дураков», Коперник «представляется достойным предметом для осмеяния и освистывания».
Нет нужды говорить, что космологическая модель Кеплера, основанная на платоновых телах, была не просто совершенно неверной, но и безумной даже по меркам современников ученого. Открытие Урана (следующей планеты после Сатурна, если считать от Солнца) в 1781 году и Нептуна (следующей после Урана) в 1846 году забили последний гвоздь в крышку гроба этой мертворожденной идеи. Тем не менее, нельзя недооценивать значение модели Кеплера в истории науки. Как отметил астроном Оуэн Джинджерич в статье, посвященной биографии Кеплера: «В истории редко случалось, чтобы столь ошибочная книга направила дальнейшее течение науки в столь верное русло». Кеплер опирался на пифагорейскую идею мироздания, и математики назвали бы это большим шагом вперед. Он разработал математическую модель Вселенной, которая, с одной стороны, была основана на имевшихся на тот момент данных наблюдений, а с другой – могла быть опровергнута последующими наблюдениями. Именно это и есть необходимые составные части «научного метода» – организованного подхода к объяснению наблюдаемых фактов на основании модели природы. Идеальный научный метод начинается со сбора фактов, затем предлагается модель, а потом то, что она предсказывает, проверяется в ходе либо искусственных экспериментов, либо дальнейших наблюдений. Иногда этот процесс описывают тремя словами: индукция, дедукция, проверка. В 1610 году Галилей при помощи своего телескопа открыл еще четыре небесных тела в Солнечной системе. Если бы было доказано, что это планеты, теории Кеплера был бы нанесен смертельный удар еще при жизни ученого. Однако, к вящей радости Кеплера, новые тела оказались спутниками Юпитера, подобными нашей Луне, а не новыми планетами, обращающимися вокруг Солнца.
Современные физические теории, нацеленные на объяснение существования всех элементарных (субатомных) частиц и основных взаимодействий между ними, также основаны на математической симметрии и в этом смысле очень похожи на теорию Кеплера, который опирался на симметричные качества платоновых тел, дабы объяснить количество и свойства планет. У модели Кеплера была еще одна общая черта с современной фундаментальной теорией Вселенной: обе теории по своей природе редукционистские, то есть они стремятся объяснить много явлений малым количеством физических законов. Например, модель Кеплера выводит и количество планет, и свойства их орбит из платоновых тел. Подобным же образом современные теории – например, теория струн – опирается на основополагающие сущности (струны), очень маленькие (более чем в миллиард миллиардов раз меньше атомного ядра), из которых выводятся все свойства элементарных частиц. Струны – подобно скрипичной струне – вибрируют и порождают разнообразные «тоны», и все известные элементарные частицы всего-навсего воплощают эти тоны.
Во время пребывания в Граце Кеплер интересовался золотым сечением, что привело к другому интересному результату. В октябре 1597 года ученый написал своему бывшему учителю Местлину о следующей теореме: «Если на отрезке, разделенном в крайнем и среднем отношении, построить прямоугольный треугольник так, чтобы прямой угол лежал на перпендикуляре, проведенном в точке разделения, то меньший катет будет равняться большему сегменту разделенного отрезка». Чертеж к этой теореме представлен на рис. 61. Отрезок АВ разделен точкой С в золотом сечении. Кеплер строит прямоугольный треугольник ADB с гипотенузой АВ так, что прямой угол D лежит на перпендикуляре, проведенном из точки золотого сечения С. Затем он доказывает, что BD (короткий катет прямоугольного треугольника) равен АС (более длинному сегменту отрезка, разделенного в золотом сечении). Кроме применения золотого сечения, такой треугольник примечателен еще и тем, что исследователь пирамид Фридрих Ребер в 1855 году приводит его при доказательстве одной из ложных теорий, предполагавших применение золотого сечения при строительстве пирамид. О трудах Кеплера Ребер не знал, однако применил похожее построение, чтобы подтвердить свое мнение о важнейшей роли «божественной пропорции» в архитектуре.
Публикация «Mysterium Cosmographicum» стала поводом для знакомства Кеплера с Тихо Браге; местом встречи, состоявшейся 4 февраля 1600 года, стала Прага, в то время – резиденция императора Священной Римской Империи. В итоге этой встречи в октябре того же 1600 года Кеплер перебрался в Прагу и стал помощником Тихо Браге (из-за своей лютеранской веры он был вынужден покинуть католический Грац). После смерти Браге 24 октября 1601 года Кеплер стал придворным математиком.
Тихо оставил массу наблюдений, в особенности связанных с орбитой планеты Марс, и Кеплер, опираясь на эти данные, открыл первые два закона движения планет, названные его именем. Первый закон Кеплера гласит, что орбиты известных планет вокруг Солнца – не окружности, а эллипсы с Солнцем в одном из фокусов (рис. 62; для наглядности эллипс вытянут гораздо сильнее, чем на самом деле). У эллипса есть две точки, так называемые фокусы, такие, что сумма расстояний любой точки эллипса до обоих фокусов всегда постоянна. Второй закон Кеплера утверждает, что планета движется быстрее всего, когда она ближе всего к Солнцу (эта точка называется перигелий), а медленнее всего – в самой дальней точке (афелии), так что линия, соединяющая планету с Солнцем, описывает (заметает) равные площади за равные промежутки времени (рис. 62). Вопрос о том, благодаря чему законы Кеплера справедливы, был главной нерешенной загадкой науки почти семьдесят лет после того, как Кеплер опубликовал свои законы. Понадобился гений Исаака Ньютона (1642–1727), чтобы сделать вывод, что планеты держатся на орбитах благодаря силе тяготения. Ньютон объяснил законы Кеплера при помощи уравнений, где законы, описывающие движение тел, сочетались с законом всемирного тяготения. Он показал, что эллиптические орбиты с переменной скоростью (согласно законам Кеплера) и предоставляют собой единственное возможное решение этих уравнений.
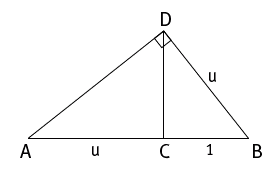
Рис. 61
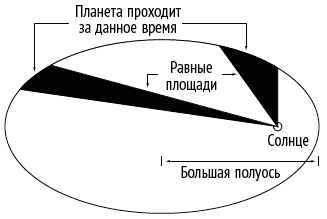
Рис. 62
Героические усилия Кеплера по расчету орбиты Марса (много сотен листов арифметических выкладок и их толкований, которые сам он называл «моей военной кампанией против Марса»), по мнению многих исследователей, знаменуют рождение современной науки. В частности, в какой-то момент Кеплер обнаружил круговую орбиту, которая соответствовала почти всем наблюдениям Тихо Браге. Однако в двух случаях эта орбита предсказывала позиции, отличавшиеся от наблюдений примерно на четверть углового диаметра полной луны. Об этом Кеплер писал так: «Стоило мне предположить, что мы можем пренебречь этими восемью минутами [дуги], и я вписал бы мою гипотезу в соответствующую 16 главу. Но поскольку пренебрегать ими непозволительно, выходит, что эти восемь минут указали путь к полнейшей реформе астрономии».
Годы, проведенные Кеплером в Праге, принесли обильные плоды и в астрономии, и в математике. В 1604 году он обнаружил «новую» звезду, известную теперь как Сверхновая Кеплера. Сверхновая – это мощный взрыв, при котором звезда, конец которой близок, сбрасывает свои внешние оболочки, которые при этом движутся со скоростью в десятки тысяч километров в секунду. В нашей родной галактике Млечный Путь подобная вспышка, по расчетам ученых, должна происходить в среднем раз в сто лет. И в самом деле, Тихо Браге открыл сверхновую в 1572 году (Сверхновая Тихо Браге), а Кеплер открыл свою в 1604 году. Однако с тех пор, по неясным причинам, других сверхновых в Млечном пути не было (кроме еще одной, которая, судя по всему, вспыхнула в 1660 годах, но осталась незамеченной). Астрономы шутят, что подобное отсутствие сверхновых, скорее всего, связано с тем, что после Тихо Браге и Кеплера не было великих астрономов.
В июне 2001 года я побывал в Праге, в доме, где жил Кеплер, по адресу Карлова улица, 4. Сейчас это оживленная торговая улица, и ржавую мемориальную дощечку над номером 4, где значится, что здесь с 1605 по 1612 год жил Кеплер, легко не заметить. Владелец магазинчика, расположенного прямо под квартирой Кеплера, даже не знал, что здесь жил один из величайших астрономов в истории. Правда, в унылом внутреннем дворике стоит маленькая армиллярная сфера с вырезанным на ней именем Кеплера, а возле почтовых ящиков висит еще одна мемориальная дощечка. Однако квартира Кеплера вообще никак не отмечена и не открыта для публики – сейчас это просто жилая квартира, каких много на верхних этажах над магазинами, и ее занимает обычное семейство.
Математические труды Кеплера внесли несколько ярких штрихов в историю золотого сечения. В тексте письма, которое Кеплер написал в 1608 году одному лейпцигскому преподавателю, мы обнаруживаем, что он открыл соотношение между числами Фибоначчи и золотым сечением. Об этом открытии он сообщает также в эссе, где изучает, почему снежинки имеют шестиконечную форму. Кеплер пишет:
Из двух правильных геометрических тел – додекаэдра и икосаэдра… эти два правильных многогранника и, по сути дела, структуру самого правильного пятиугольника невозможно выстроить без божественной пропорции, как называют ее нынешние геометры. Она устроена так, что два меньших члена прогрессии вместе составляют третий, а два последних, если их сложить, составляют непосредственно следующий за ними, и так далее до бесконечности, если не нарушать и продолжать эту пропорцию… Чем дальше мы отходим от номера первого, тем совершеннее становится пример. Пусть самыми маленькими числами будут 1 и 1… сложи их, и сумма будет 2, прибавь это число к последнему из 1, получишь 3, прибавь к нему 2 и получишь 5, прибавь три – получишь 8; 5 к 8–13; 8 к 13–21. Как 5 к 8, так и 8 к 13 – приблизительно, – и как 8 к 13, так и 13 к 21 – приблизительно.
Иначе говоря, Кеплер обнаружил, что отношение последовательных чисел Фибоначчи сходится к золотому сечению. По сути дела, он открыл и еще одно интересное свойство чисел Фибоначчи – что квадрат любого члена последовательности отличается не более чем на 1 от произведения двух соседних членов последовательности. Например, поскольку последовательность Фибоначчи – 1, 1, 2, 3, 5, 8, 13, 21, 34 …, то если мы рассмотрим 32 = 9, то 9 лишь на 1 отличается от произведений двух членов последовательности, соседних с 3: 2 × 5 = 10. Подобным же образом 132 = 169 отличается на 1 от 8 × 21 = 168 и т. д. Это качество чисел Фибоначчи подводит нас к удивительному парадоксу, который первым обнаружил великий изобретатель математических головоломок Сэм Лойд (1841–1911).
Рассмотрим квадрат со стороной 8 (с площадью 82 = 64) на рис. 63. Теперь разрежем его на четыре части по намеченным линиям. Из этих четырех кусочков можно составить прямоугольник (рис. 64) со сторонами 13 и 5 – то есть с площадью 65! Откуда взялся дополнительный квадратик?! Ответ на этот парадокс состоит в том, что на самом деле детали головоломки не сходятся идеально вдоль длинной диагонали прямоугольника, получается длинный узкий параллелограмм, которого не видно из-за жирной линии, обозначающей длинную диагональ на рис. 64, и его площади как раз хватает на площадь одного квадратика-единицы. Само собой, 8 – число Фибоначчи, и его квадрат 82 = 64 отличается на 1 от произведения двух соседних чисел Фибоначчи (3 × 5 = 65): свойство, которое открыл Кеплер.
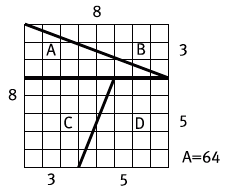
Рис. 63
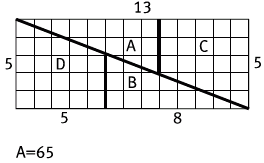
Рис. 64
Наверное, вы уже заметили, что Кеплер именует золотое сечение «божественной пропорцией, как называют ее нынешние геометры». Все научные изыскания Кеплера окрашены сочетанием рациональных рассуждений с христианскими убеждениями. Кеплер был естествоиспытателем-христианином и считал своим долгом понять не только устройство Вселенной, но и намерения ее Творца. Свою гипотезу о Солнечной системе он строил под влиянием сильной тяги к числу 5, перенятой у пифагорейцев, и о золотом сечении писал следующим образом:
Особенность этого соотношения заключается в том, что похожую пропорцию можно построить из целого и большей части, и то, что раньше было большей частью, теперь становится меньшей, а то, что раньше было целым, теперь становится большей частью, а сумма их обладает соотношением целого. Так происходит до бесконечности, а божественная пропорция всегда сохраняется. Я полагаю, что эта геометрическая пропорция и послужила идеей Творцу, когда Он творил подобное из подобного по образу и подобию Своему – и это тоже происходит до бесконечности. Число пять я вижу почти во всех цветках, которые прокладывают путь плодам, то есть творению, и которые существуют не ради себя самих, а ради того, чтобы за ними последовали плоды. Сюда можно включить почти все цветы плодовых деревьев; следует, вероятно, исключить лимоны и апельсины, хотя я не видел их цветов и сужу лишь по плодам или ягодам, которые поделены не на пять, а на семь, одиннадцать или девять долек. Однако воплощение числа пять в геометрии, то есть правильный пятиугольник, строится посредством божественной пропорции, которую мне бы хотелось [предположительно считать] прототипом Творения. Более того, [она] наблюдается и между движением Солнца (или, как я полагаю, Земли) и Венеры, которая стоит на вершине порождающей способности соотношения 8 и 13, которое, как мы еще услышим, подходит очень близко к божественной пропорции. Наконец, согласно Копернику, сфера Земли расположена посередине между сферами Марса и Венеры. Пропорцию между ними можно получить из додекаэдра и икосаэдра, оба из которых в геометрии производятся из божественной пропорции – однако акт творения происходит именно на нашей Земле.
Теперь рассмотрим, как из божественной пропорции проистекают изображения мужчины и женщины. На мой взгляд, размножение растений и продолжение рода у животных состоят в том же соотношении, что и геометрическая пропорция, пропорция, выраженная частями отрезка, или арифметическая или численно выраженная пропорция.
Проще говоря, Кеплер искренне верил, что золотое сечение послужило для Бога фундаментальным инструментом сотворения Вселенной. Из этого отрывка следует также, что Кеплер знал о проявлениях золотого сечения и чисел Фибоначчи в расположении лепестков растений.
Относительно спокойный и плодотворный с профессиональной точки зрения период жизни в Праге кончился для Кеплера в 1611 году, когда его постигла череда несчастий. Сначала умер от оспы его сын Фридрих, затем от заразной лихорадки, которую принесли австрийские оккупанты, скончалась его жена Барбара. В конце концов, император Рудольф отрекся от престола в пользу своего брата Матиаса, известного нетерпимым отношением к протестантам. Поэтому Кеплер был вынужден перебраться в Линц, на территорию современной Австрии.
Венцом трудов Кеплера, созданных в Линце, стала публикация в 1619 году его второй главной работы по космологии – «Harmonice Mundi» («Гармония мира»).
Вспомним, что для Пифагора и пифагорейцев музыка и гармония была первым доводом в пользу того, что космические явления можно описать математически. Созвучные тоны порождали лишь те струны, длины которых соответствовали простым дробям. Соотношение 2:3 звучало как квинта, 3:4 как кварта и т. д. Считалось, что похожее гармоническое расположение планет также порождает «музыку сфер». Кеплер был хорошо знаком с этой концепцией, поскольку прочитал почти всю книгу отца Галилео Галилея Винченцо «Диалоги о древней и современной музыке», хотя и не был согласен с некоторыми идеями Винченцо. Поскольку он был также убежден, что создал исчерпывающую модель Солнечной системы, то смог даже рассчитать небольшие «мотивы» для разных планет (рис. 65).

Рис. 65
Поскольку Кеплер был уверен, что «еще до начала вещей геометрия была столь же вечной, сколь и Божественный Разум», «Гармония мира» была по большей части посвящена геометрии. Один аспект этого труда был особенно важен для истории золотого сечения – я имею в виду изыскания Кеплера в области геометрического паркета.
Паркетом в геометрии называют узор или структуру, состоящую из «плиток» одной или нескольких форм, которые полностью покрывают плоскость, не оставляя промежутков – подобно мозаике из плиток на полу. В главе 8 мы увидим, что некоторые математические концепции, наблюдаемые в таких «паркетах», теснейшим образом связаны с золотым сечением. Хотя Кеплер не знал обо всех математических тонкостях паркетов, интерес к отношениям между разными геометрическими фигурами и почитание правильного пятиугольника, который воплощает божественную пропорцию нагляднее всего, позволил ему создать интересную работу о паркете. Особенно Кеплера занимала конгруэнтность («подогнанность» друг к другу) геометрических фигур и тел вроде многогранников и многоугольников. На рис. 66 показан пример из «Гармонии мира». Этот узор паркета составлен из четырех фигур – и все они связаны с золотым сечением: это правильные пятиугольники, пентаграммы, десятиугольники и сдвоенные десятиугольники. Для Кеплера это воплощение «гармонии», поскольку по-гречески это слово означает «соответствие друг другу».
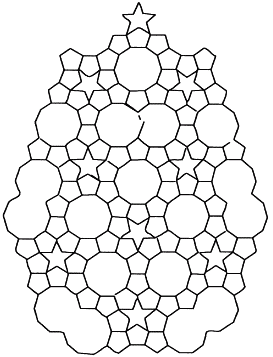
Рис. 66
Интересно, что интерес к паркетам проявляли до Кеплера еще два человека, также сыгравшие важную роль в истории золотого сечения (и уже упоминавшиеся на страницах нашей книги): это Абу-л-Вафа и художник Альбрехт Дюрер. Оба они рассматривали узоры из фигур с пятилучевой симметрией (пример из набросков Дюрера приведен на рис. 67).
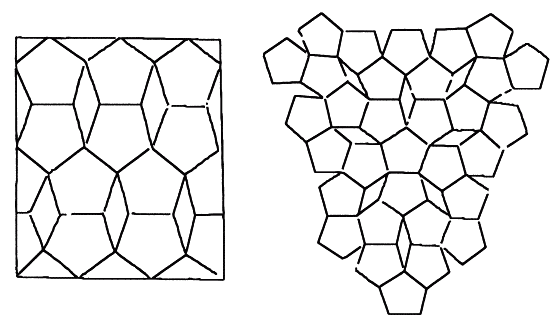
Рис. 67
В пятой книге «Гармонии мира» содержится самый значительный результат астрономических исследований Кеплера – Третий закон движения планет. Здесь сполна выразились все его мучительные раздумья по поводу размеров орбит разных планет и периодов их обращения вокруг Солнца. Двадцать пять лет работы сконцентрировались в поразительно простом законе: квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет, и это отношение одинаково для всех планет (большая полуось – это половина длинной оси эллипса, см. рис. 62). Кеплер открыл этот основополагающий закон, послуживший Ньютону отправной точкой для формулировки закона всемирного тяготения, когда «Гармония мира» была уже в печати. Не в силах сдержать ликования, ученый объявил: «Я похитил золотые сосуды египтян, чтобы вдали от Египта выстроить жертвенник Господу моему». Суть закона естественно следует из закона всемирного тяготения: сила тяготения тем больше, чем ближе планета к Солнцу, вот почему планеты, которые ближе к нему, вынуждены вращаться быстрее, иначе они упадут на Солнце.

Рис. 68
В 1626 году Кеплер переехал в Ульм и завершил там работу над «Рудольфовыми таблицами» – на тот момент это были самые подробные и точные астрономические таблицы в истории. Когда я в июне 2001 года был в Венском университете, мне показали первое издание таблиц, хранящееся в библиотеке обсерватории (до наших дней дошло 147 экземпляров). На фронтисписе книги (рис. 68) символически изображена история астрономии, а в левом нижнем углу, возможно, находится единственный автопортрет Кеплера (рис. 69). На нем Кеплер трудится при свете свечи под виньеткой, где перечислены главные его публикации.

Рис. 69
Умер Кеплер в полдень 15 ноября 1630 года и похоронен в Регенсбурге. Судьба и после смерти не оставила его в покое, будто бы мало было бурной жизни: войны стерли с лица земли его могилу. К счастью, сохранился набросок надгробия, который выполнил друг Кеплера, и на нем есть и эпитафия ученому:
Я небеса измерял, ныне тени Земли измеряю.
Дух мой на небе жил, здесь же тень тела лежит.
В наши дни, пожалуй, невозможно представить себе ученого, столь оригинального и плодовитого, как Кеплер. Надо понимать, что на долю этого человека выпали невообразимые страдания: в частности, в 1617–1618 году он меньше чем за полгода потерял троих детей. Наверное, лучше всего о нем сказал английский поэт Джон Донн (1572–1631) в памфлете «Игнатий и его конклав»: Кеплер «вменил себе в обязанность следить, чтобы в небесах без его ведома ничего нового не происходило».

