Метод Монте-Карло (Monte Carlo Analysis – MCA) использует модель проекта, например сетевой график, для анализа поведения. С этой целью MCA делает случайную выборку из распределения вероятности для каждой операции при условии выполнения проекта сотни и даже тысячи раз [5], что позволяет получить статистическое распределение и приблизительное значение длительности проекта (рис. 9.5). С помощью таких распределений можно количественно описать риски, характеризующие различные варианты расписаний, альтернативных стратегий исполнения, путей выполнения операций и даже отдельные операции. Например, на рис. 9.5 показана 40%-ная вероятность того, что проект будет завершен не позже 20 мая.

Обычно MCA имеет дело с рисками для расписания, стоимости и потока денежной наличности, хотя могут анализироваться и другие аспекты, например качество конечного продукта проекта. В целом выполнить анализ рисков расписания сложнее, чем анализ рисков стоимости, поскольку в таком случае потребуется установить взаимозависимости между операциями проекта с целью идентификации критического пути. По этой причине мы рассмотрим метод Монте-Карло применительно к анализу рисков расписания (рис. 9.6).

Сбор исходной информации.Ключевая роль в анализе Монте-Карло принадлежит следующим информационным элементам:

•плану управления рисками;

•плану реагирования на риски;

•логической схеме (сетевой диаграмме) или расписанию проекта;

•распределениям вероятностей.

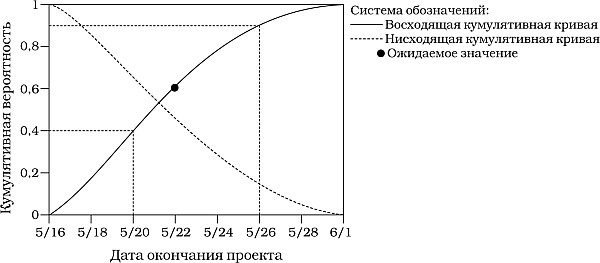
Рис. 9.5.Кумулятивное распределение длительности проекта, полученное в ходе анализа Монте-Карло[30]

Рис. 9.6.Проведение анализа Монте_Карло для рисков расписания

Поскольку план управления рисками регламентирует работу с рисками в течение жизни проекта, он же должен предложить способы использования анализа Монте-Карло. Другой тип указаний содержится в плане реагирования на риски: в частности, здесь отдельные риски идентифицируются, описываются и анализируются с целью оценивания, ранжирования (посредством матрицы «Вероятность – воздействие») и численного описания, наряду с выбором стратегий превентивных действий и действий, выполняемых при наступлении события риска. Вся эта информация применяется в анализе Монте-Карло для генерации диапазона возможных значений длительности проекта (см. врезку «Ключевые понятия метода Монте-Карло»). Здесь нужен сетевой график, который упорядочивает операции проекта, одновременно отображая их взаимозависимости. Некоторые менеджеры предпочитают начинать не с сетевого графика, а с детерминистского расписания проекта, отображаемого, например, в формате каскадной диаграммы «операции на стрелках» во временном масштабе (рис. 9.7). Подходящим вариантом является также использование расписания по методу критического пути.

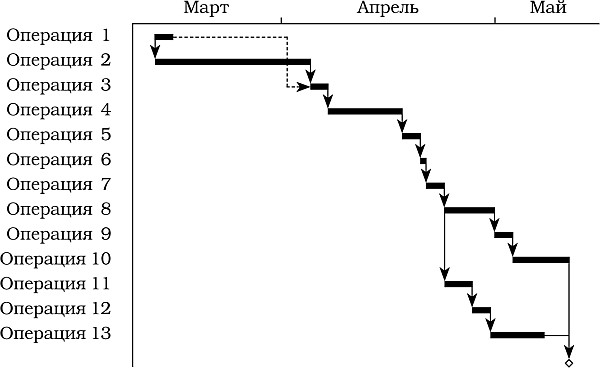
Рис. 9.7.Пример диаграммы «операции на стрелках» во временном масштабе для анализа рисков по методу Сонте-Карло

Получить диапазон возможных значений длительности проекта и соответствующих вероятностей нельзя без подготовки распределений вероятности для длительностей операций проекта. Чтобы подготовить такие распределения, нужно ответить на вопрос: «Сколько времени потребуется для выполнения той или иной операции?» Предположим, что вы проводили эту операцию уже много раз и всегда за 10 дней. Если бы для каждой операции проекта имелась такая одноточечная (однозначная) оценка, то при ее применении для расчетов длительность проекта также выражалась бы только одним числом. В описанной однозначной детерминистской модели все длительности операций проекта фиксированы. Однако в большинстве современных проектов такой сценарий невозможен, поэтому более реалистичной выглядит следующая вероятностная модель.

• случайное событие– процесс или измерение, результат которого заранее не известен;

• непрерывное распределение– способ представления какой-либо величины в пределах заданного диапазона;

• дискретное распределение– распределение, при котором величина принимает одно из идентифицируемых значений, каждое из которых имеет вычислимую вероятность возникновения;

• детерминистская модель– модель, в которой все параметры являются фиксированными и имеют одиночные оценки;

• ожидаемое (среднее) значение (EV)– взвешенное с учетом вероятности среднее значение всех возможных результатов;

• мода– конкретный результат, являющийся наиболее вероятным, то есть самая высокая точка на кривой распределения;

• модель– упрощенное представление исследуемой системы, например диаграмма критического пути: она отражает результат проекта (в частности, его длительность) и значение этого результата (допустим, 18 месяцев);

• вероятность (возможность, шанс)– число в диапазоне от 0 до 1 (или эквивалентное процентное значение), показывающее вероятность наступления некоторого события;

• распределение вероятности (функция плотности вероятности, вероятностная функция)– математически или графически представленный диапазон значений (допустим, от 2 до 14 дней), которые может принимать переменная (например, длительность операции), и вероятность того, что эта переменная примет то или иное конкретное значение;

• сценарий проекта (итерация, испытание)– будущее состояние проекта;

• случайная выборка– процесс генерации случайного числа в диапазоне между 0 и 1, который определяет значение входной переменной на основе распределения вероятности;

• случайная величина (случайная переменная, стохастическая переменная)– мера случайного события;

• однозначная (точечная) оценка– оценка в виде одиночного числа, имеющая только одно значение;

• стандартное отклонение– квадратный корень из дисперсии;

• стохастическая (вероятностная) модель– модель, которая включает в себя случайные переменные;

• дисперсия– ожидаемое значение суммы возведенных в квадрат отклонений от среднего значения.

Представим, что операция 1 повторялась чрезвычайно часто, и ее длительность оказалась заключена в диапазоне от 5 до 39 дней (диапазон результатов). Для каждого значения, которое принимала длительность операции 1, мы зафиксировали соответствующую долю испытаний. Эта доля для конкретного результата приблизительно равна вероятности (p) его наступления для операции 1. Полученные приблизительные вероятности (чем больше испытаний будет проведено, тем ближе к истинной вероятности окажется значение найденной доли) для всех возможных выходов нужно отобразить в виде распределений вероятности (см. соответствующую кривую для операции 1 на рис. 9.6). Предположим далее, что распределения вероятностей, основанные на опыте, существуют и для других операций проекта (см. длительность операции 2 на рис. 9.6). В таком случае они были бы близки к объективным вероятностям, которые по определению получаются на основе полного знания о системе и не зависят от субъективного мнения (см. врезку «Часто используемые распределения вероятности»).

Однако длительности некоторых операций могут быть однозначными (например, длительность операции n на рис. 9.6), а значит, допустима комбинация распределенных и однозначных длительностей. До тех пор пока длительность одной или нескольких операций (входов модели) представляет собой распределенную величину, длительность проекта (выходы) также будет распределенной величиной [10].

Некоторые компании имеют основанные на опыте базы данных, в которых хранятся приблизительные распределения для длительностей их проектных операций, но это скорее исключение, чем правило. На практике распределения подготавливаются на основе субъективных вероятностей, то есть личного мнения о том, примет ли длительность проекта данное значение.

Здесь рекомендуется заручиться помощью экспертов или опытных участников проекта. Проведение мозгового штурма совместно с «владельцами» операций, изучение длительностей подобных операций в прошлых проектах, консультирование с другими специалистами компании, не участвующими в проекте, – все это помогает выявить распределения вероятности или однозначные оценки длительностей [4].

Распределения, взятые из прошлых проектов, легко модифицировать для отражения информации из плана реагирования на риски, который является критически важным входным информационным элементом для анализа Монте-Карло. Например, для каждого отдельного события риска, рассматриваемого в плане, определяется статус. При необходимости основанное на прошлых проектах распределение для рассматриваемой операции может быть расширено, чтобы включить воздействие статуса события риска. В случае произвольного распределения для длительности конкретной операции это означает увеличение максимума при отражении статуса события риска. Информация из плана реагирования на риски позволяет выявить распределения вероятности, наиболее подходящие для каждой операции, с учетом фактических рисков конкретного проекта.

Для описания популярного треугольного распределения (рис. 9.8a) используются три величины: минимальное значение L (5), наиболее вероятное значение M (10) и максимальное значение H (20). Приведенные числа показывают длительность операции в днях. Среднее значение равно (L + M + H) / 3. Бета-распределение (рис. 9.8б), используемое для оценки длительностей операций в методе PERT, требует для расчета тех же трех параметров, а именно: минимальное значение (5), наиболее вероятное значение (10) и максимальное (20), однако среднее вычисляется как (L + 4M + H) / 6. Логарифмически нормальное распределение (рис. 9.8в) описывается двумя параметрами – средним значением (10) и стандартным отклонением (2). Известное своей гибкостью произвольное распределение (рис. 9.8г) допускает изменение формы кривой таким образом, чтобы отразить мнение экспертов [4], и описывается массивом значений (7, 10, 15) с соответствующими им вероятностями (2, 3, 1), которые находятся в диапазоне между минимумом (5) и максимумом (20).

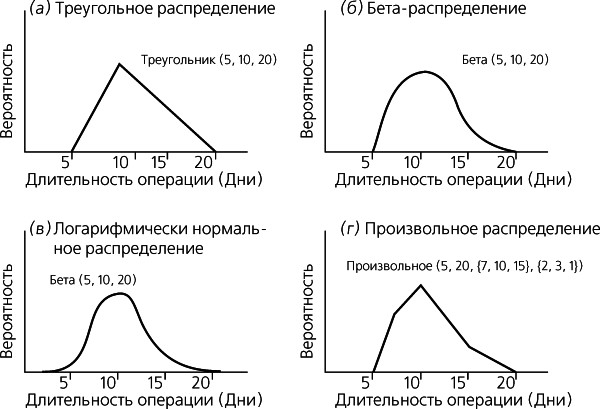
Рис. 9.8.Распределения вероятности, часто используемые при анализе рисков расписания методом Монте-Карло

Выбор случайного значения из каждого распределения.Когда распределения вероятности получены для всех операций проекта (переменных), для каждой операции нужно случайным образом выбрать одно значение длительности, принадлежащее определенному диапазону значений. Используя метод случайной выборки (совокупность случайных значений), анализ Монте-Карло генерирует случайное число в диапазоне от 0 до 1, которое вводится в математическое уравнение для расчета длительности операции согласно распределению [4]. Выборка может составляться и с помощью такого эффективного метода, как Latin hypercube sampling [4]. Вне зависимости от метода случайная выборка из распределения вероятности выполняется тем способом, который воспроизводит форму кривой распределения [4].

Проведение испытания для генерации значения длительности проекта.Составление случайной выборки значений длительностей приводит к тому, что для каждой операции в расписании устанавливается только одно значение. Наложение описанной комбинации значений на сетевой график позволяет получить сценарий длительности проекта. По сути, это детерминистское расписание с фиксированным значением длительности проекта, построенное на фиксированных значениях длительности каждой операции.

Повторяя процедуру взятия случайной выборки и проведения испытаний, мы получим множество сценариев длительности проекта, каждый из которых будет правдоподобным. Возникает вопрос: «Сколько испытаний необходимо?» Обычно испытания (итерации) выполняются до тех пор, пока не будет достигнуто их предустановленное количество (N в точке принятия решения на рис. 9.6), которое зависит от числа переменных (операций) и требуемой степени уверенности, но обычно лежит в диапазоне от 100 до 1000 [4]. За счет достаточно большого количества итераций нужно сохранить характеристики оригинальных распределений вероятности для длительности операций и качественно аппроксимировать такое распределение для проекта [10].

Обработка результатов.После завершения испытаний у нас будет N значений длительности проекта, каждое из которых отражает возможный вариант расписания. Обработка полученных данных программным способом может дать следующие результаты (см. правую часть рис. 9.6):

•ожидаемое значение (EV) длительности проекта. Усреднение значений длительности проекта, полученных в ходе испытаний, дает приблизительное значение ожидаемой длительности – то есть взвешенное с учетом вероятностей среднее всех результатов. Чем больше количество испытаний, тем выше точность наиболее вероятного значения и аппроксимации формы распределения для длительности проекта;

•частотное распределение. Эту гистограмму, показывающую относительную частоту встречаемости, получают путем группировки сгенерированных значений длительности проекта в определенное количество столбцов или классов. Частота соответствует количеству значений в каждом классе. Поделив ее на общее количество значений, мы узнаем, насколько вероятно то, что длительность проекта (выходная переменная) будет находиться в диапазоне, соответствующем данному классу (рис. 9.9);

•кумулятивная частота. Данная диаграмма может быть выполнена в восходящем или нисходящем форматах (см. рис. 9.5). Первый показывает вероятность того, что длительность проекта будет равна значению на оси X или меньше его, а последний – вероятность того, что длительность равна значению на оси X или больше его. Мы рассмотрим восходящий формат, поскольку он используется чаще. Ожидаемое значение отмечено на графике черной точкой;

•диаграмма торнадо. Эта диаграмма показывает, до какой степени неопределенность длительностей отдельных операций влияет на неопределенность длительности проекта (рис. 9.10), а точнее – насколько сильно операция (входная переменная) влияет на расписание проекта (выход модели). Следовательно, чем длиннее вертикальная полоска, тем сильнее влияние операции на длительность проекта. Согласно сложившейся практике, размер полоски соответствует степени воздействия, поэтому при наличии как положительных, так и отрицательных влияний диаграмма слегка напоминает торнадо. Чтобы не загромождать диаграмму, ограничьтесь изображением тех операций (переменных), которые оказывают влияние от максимального до четверти максимального [4].

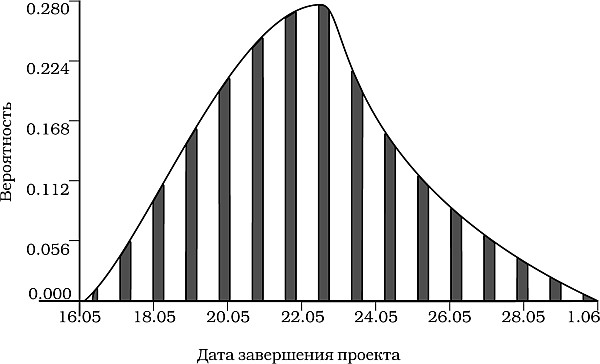
Рис. 9.9.Гистограмма частотного распределения длительности проекта

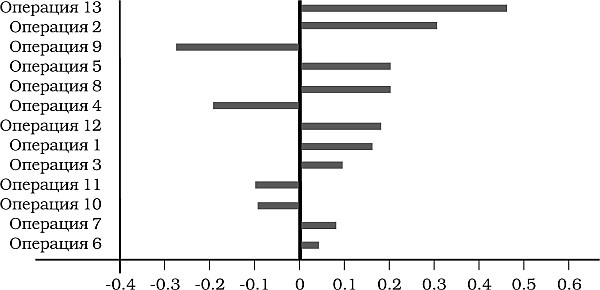
Рис. 9.10.Пример диаграммы торнадо

Анализ и интерпретация результатов.Результаты анализа рисков расписания должны интерпретироваться так, чтобы дать ясные ответы на поставленные вопросы. По этой причине целесообразно следовать четырем принципам анализа рисков [4]:

•фокусироваться на проблеме;

•сводить статистику к минимуму;

•использовать графическое отображение везде, где необходимо;

•понимать допущения, принятые в модели (например, в диаграмме «операции на стрелках» во временном масштабе).

Предположим, что проектная команда намеревается выполнить анализ рисков расписания, чтобы получить ответы на следующие вопросы:

•Насколько вероятно, что команда сумеет завершить проект к крайнему сроку (20 мая), установленному руководством?

•Если вероятность благоприятного исхода составит менее 90% (такое значение предпочтительно с точки зрения команды), как договориться с руководством о сдвиге крайнего срока?

•Если вопрос о переносе крайнего срока будет успешно решен, как определить три операции, наиболее сильно влияющие на длительность проекта?

Для того чтобы получить ответ на первый вопрос, необходимо на графике кумулятивной частоты (рис. 9.5):

•отметить на оси X дату, которая соответствует крайнему сроку (20 мая), установленному руководством;

•сдвинуться от этой даты вверх до пересечения с кривой кумулятивной частоты;

•сдвинуться от точки пересечения влево до пересечения с осью Y. Значение, находящееся на оси Y (40%), и есть вероятность того, что проект удастся завершить к установленному сроку.

Совершенно ясно, что вероятность очень мала, – значительно ниже, чем предпочитаемые 90%. Далее члены команды обращаются к руководству с просьбой добавить к крайнему сроку еще шесть дней (резерв неопределенности), в результате чего проект будет завершен к 26 мая с вероятностью 90% (второй вопрос). Чтобы иметь твердую позицию при ведении переговоров с руководством, команда разрабатывает еще один вариант действий: использует сжатие расписания (выделение большего количества ресурсов в операции проекта) в сочетании с быстрым проходом (наложением операций в максимально возможной степени), получая новую логическую диаграмму проекта и новые распределения вероятности для операций, и повторно выполняет MCA. Построив график кумулятивной вероятности, команда выясняет, что теперь вероятность завершения проекта к установленному сроку (20 мая) составляет 90%. Вооруженные этим графиком, не содержащим излишней (избыточной) статистики, затем члены команды идут к руководству, показывают оба возможных варианта и получают обещание выделить в проект дополнительные ресурсы в соответствии со вторым вариантом.

Диаграмма торнадо (рис. 9.10) выявляет три операции, оказывающие наибольшее влияние на дату завершения проекта и потому требующие особого внимания при выполнении проекта (третий вопрос). Команда понимает, что проводимый анализ Монте-Карло основан на: (а) измененной логике диаграммы «операции на стрелках» во временном масштабе и (б) измененных распределениях вероятности для операций, базирующихся на новых обязательствах по выделению ресурсов.

Иными словами, в своих действиях команда руководствовалась четырьмя принципами анализа рисков расписания.

Когда использовать.Традиционно сложилось так, что большие и сложные проекты чаще выигрывали от применения MCA. Крупные проекты, в отличие от малых, имеют более значимые цели и могут позволить себе израсходовать часть ресурсов на выполнение анализа Монте-Карло. Чтобы такая точка зрения изменилась, должен был произойти ряд событий. Во-первых, тенденция к управлению проектами привела к размножению и процветанию небольших, но важных проектов. Появились мощные компьютерные программы, помогающие выполнять MCA. И наконец, проектные офисы, способные проводить анализ Монте-Карло для поддержки множества проектов, стали встречаться в организациях все чаще и чаще. Все названные события помогли сделать MCA доступным для малых проектов, что изменило характер его применения в корпорациях. Сегодня анализ Монте-Карло используется как в крупных, так и в небольших проектах в качестве инструмента реагирования на конкретную ситуацию. Если проект чувствителен к крайнему сроку завершения, анализ Монте-Карло будет предпочтительным вариантом. Аналогично, когда есть множество сценариев проекта, которые необходимо исследовать по принципу «что, если», MCA будет удобнее, чем дерево решений [10]. В ситуации, когда определяющими при выборе проекта, например, в процессе отбора внутри компании, становятся очень тонкие нюансы, анализ Монте-Карло также представляется верным выбором.

Время использования.Задача, возложенная на MCA, в основном определяет длительность его выполнения. Обычно перед специалистами офиса или административными помощниками ставится задача выполнить анализ на основе данных, предоставленных проектной командой. Для небольших проектов, содержащих порядка 50 операций, ввод данных и проведение анализа Монте-Карло может занять от 10 до 30 минут. Если логическая диаграмма проекта уже существует, подготовка распределений вероятности в ходе мозгового штурма и организация их в виде таблицы для передачи в главный офис может занять от часа до двух. При увеличении размера и сложности проекта неизбежно возрастет и время проведения MCA.

Выгоды.Первоначальные расписания и бюджеты проекта часто оказываются нереалистичными, точнее неадекватными, из-за неопределенности, свойственной операциям проекта. Чтобы как-то отреагировать на эту неопределенность, многие команды присваивают операциям произвольные значения длительности или стоимости и надеются на лучшее [8]. Метод MCA, напротив, обеспечивает многостороннее, детальное представление связанной с рисками проблемы, что важно в ряде ситуаций (см. врезку «Наверняка или вероятно?»). Рассмотрим, к примеру, ситуацию, когда решается судьба компании: если результатом нового проекта не станет разработка продукта, который появится на рынке раньше продуктов конкурентов, компания перестанет быть лидером в своей области. Метод Монте-Карло способен значительно повысить качество принимаемых решений, предлагая четкий анализ рисков, различных сценариев и вероятности достижения цели. От менеджера в любой момент могут потребовать выполнить проект быстрее, чем это возможно, или при явно заниженном бюджете. В этом случае анализ Монте-Карло позволит составить план снижения рисков и собрать аргументы против необъективного подхода и за выделение ресурсов, необходимых для завершения проекта желаемым образом. Таким образом, ценность MCA состоит в его способности исследовать каждый сценарий проекта, включая экстремальные варианты, чтобы посмотреть, какие условия приводят к тем или иным результатам. Это позволяет не только проверить проект на реалистичность, но также отделить возможное от невозможного и понять, как сделать невозможное возможным [10].

Преимущества и недостатки.Метод Монте-Карло характеризуется рядом преимуществ [4]:

•простая математика. Вычисления, необходимые для анализа Монте-Карло, весьма просты. Даже введение сложных уравнений или моделирование корреляции и иных взаимозависимостей (например, степенных или логарифмических функций, утверждений типа «Если» и т. д.) не создает дополнительных трудностей;

•легкость использования. Существуют хорошие программные пакеты, автоматизирующие проведение MCA, то есть компьютер в состоянии выполнить всю работу, необходимую для генерации результирующего распределения;

•легкость изменения. Внесение изменений в модель, анализируемую методом Монте-Карло, – это быстрый процесс, позволяющий сравнивать текущую модель с предыдущими. Исследование поведения каждой из моделей также не представляет сложностей;

•законность. Метод Монте-Карло – достаточно известный и популярный инструмент, а значит, проектная команда и руководство с большим вниманием отнесутся к его результатам.

Часто метод Монте-Карло подвергается критике за следующие недостатки:

•сложность. Хотя метод Монте-Карло основан на простой математике, он строится на концепции вероятности, которой многим менеджерам проектов еще предстоит овладеть;

•приблизительность. Выходные распределения вероятности приблизительны, как говорят критики. Это действительно так в случае малого числа итераций, однако проблема легко решается путем увеличения количества итераций вплоть до достижения требуемого уровня точности;

•времяемкость. Компьютеру нужно много времени для генерации итераций.

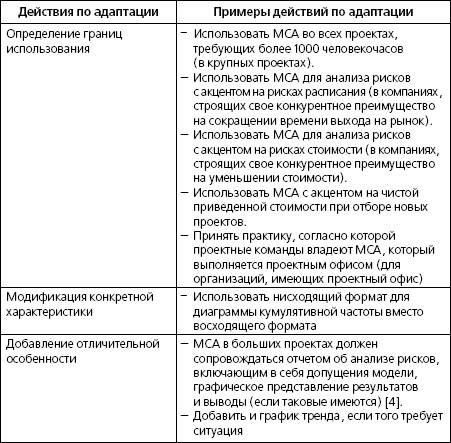
Адаптация метода Монте-Карло.MCA – это инструмент анализа рисков, который имеет огромную ценность и рекомендуется к использованию в большей части проектов, сталкивающихся с неопределенным окружением, где происходит выполнение. Общий вид метода Монте-Карло, описанный выше, необходимо адаптировать к конкретной ситуации. С этой целью мы предлагаем несколько вариантов подобной подстройки.

Джон Гленн, старший менеджер фирмы, работающей в сфере высоких технологий, рассказывает: «В нашей компании раньше было принято интересоваться у менеджеров о том, насколько они уверены в завершении проекта к крайнему сроку. Менеджеры оценивали риск невыполнения, например, таким образом: «Я на 70% уверен, что закончу проект к 1 мая» – причем слово уверен на самом деле использовалось в значении вероятно или возможно. Ответ в значительной степени основывался на интуиции, поскольку они никогда не пользовались какими-либо инструментами для оценки степени уверенности. При этом нам казалось, что мы заметно повысили свою осведомленность о рисках и осознали необходимость плана реагирования на риски.

Однако показатель уверенности – это не субъективное ощущение, а число в диапазоне от 0 до 1, которое показывает степень уверенности в истинности утверждения или суждения. Ноль соответствует отсутствию информации или знания, а единица – полной уверенности. С другой стороны, вероятность означает возможность наступления события. И хотя эти два слова имеют очень разные значения, я не пытался изменить способ их использования в компании. Почему? Во-первых, чтобы не провоцировать сопротивление со стороны людей, которые считали данный метод превосходным. И, во-вторых, потому, что все сотрудники использовали слово уверен в значении вероятно.

Мы не стали менять методологию. Однако я полагал, что основываться на интуиции при оценке степени уверенности примитивно и непоследовательно. Поэтому я провел активную работу по внедрению анализа Монте-Карло в нашу систему оценки. Теперь для того, чтобы оценить, насколько вероятно завершение проекта к установленному сроку, мы выполняем MCA, но не используем слово «вероятно», а, как и раньше, говорим, что мы уверены».

Убедитесь, что метод Монте-Карло основан на:

• плане реагирования на риски;

• модели проекта;

• распределениях вероятности для переменных.

Он также должен производить результаты, включающие в себя как минимум:

• ожидаемое значение;

• диаграмму частотного распределения;

• кривую кумулятивной частоты.

Результаты анализа рисков должны интерпретироваться так, чтобы дать четкие ответы на поставленные вопросы.

Предметом рассмотрения данного раздела являлся анализ Монте-Карло – инструмент, использующий модель проекта, например сетевой график, для анализа его поведения и рисков. Описанный инструмент призван снизить риски посредством сбора аргументов против необъективного подхода и получения ресурсов, необходимых для выполнения проекта желаемым образом. Для этого MCA исследует каждый сценарий проекта, включая экстремальные варианты, чтобы посмотреть, какие условия приводят к тем или иным результатам. Такой подход помогает не только убедиться в реалистичности проекта, но также отделить возможное от невозможного. В основном метод Монте-Карло полезен для больших и сложных проектов. Ключевые положения данного раздела представлены во врезке «Проверка метода Монте-Карло».