В этой главе у нас две задачи: (1) снабдить нас удобным инструментом для оценки рисков и (2) дать некоторые основные знания о пользовании им. Инструмент, названный RISKOLOGY, можно бесплатно скачать с нашего сайта в Интернете (http://www.systemsguild.com/riskology/). Это – модель риска в смысле, описанном в предыдущей главе. Инструмент предназначен для использования вместе с вашей собственной производственной моделью или механизмом параметрического оценивания. Наш инструмент не оценивает, сколько времени будет длиться ваш проект, он всего лишь говорит вам о том, сколько неопределенности следует приписать любой выдвигаемой оценке.

Модель представлена в виде электронной таблицы. Она исходит из логики, необходимой для работы с набором рисков в количественном выражении, включая исходную базу данных для четырех главных рисков разработки программного обеспечения. (Мы обсудим главные риски в главе 13).

Как можно водить машину без понимания всех тонкостей ее устройства, так можно использовать модель риска без глубокого понимания того, как она работает. В этой главе мы все же дадим вам возможность заглянуть внутрь модели. Это поможет слегка уменьшить суеверный страх и дать вам точку опоры, если вы решите самостоятельно подстроить электронные таблицы, чтобы они лучше соответствовали вашим задачам. Индивидуальная подгонка может быть важна, поскольку позволяет вам уничтожить, по крайней мере, некоторые из явных неопределенностей, относящихся к вашим проектам. Ваши собственные данные могут оказаться более оптимистичными и более применимыми, чем наша общеотраслевая информация.

Прежде, чем погрузиться в детали, обещаем не напрягать ваши мозги: мы не использовали «крутой» математики в этой главе. Если вы хоть немного знаете арифметику, эта глава будет вам посильна. Если вы собрались использовать электронную таблицу, например, для прогнозирования размера своей пенсии, у вас не должно быть проблем с тем, чтобы разобрать эту модель риска и собрать ее обратно, если решите заняться ее подгонкой.

В центре любой модели риска – метод определения объединенного воздействия двух и более неопределенностей:

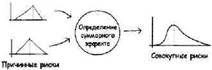
К концу следующей главы будет показано, как это работает в проектах разработки программного обеспечения. А прямо сейчас мы намерены предложить для иллюстрации рассказ об очевидно надуманной проблеме, которую зато легче понять.

Предположим, что вы – бегун. Вы честно бегаете ежедневно, но время пробежки варьируется в зависимости от других ваших дел. Ваша ежедневная тренировка занимает от 15 минут до 1 часа. Вы ведете записи и обнаруживаете, что совершенно независимо от расстояния (в указанном временном диапазоне) скорость бега варьируется от 6,5 до 9 миль/час. Записи вы ведете так давно, что накоплена вполне приличная статистика:

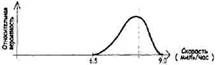
Реальные данные, возможно, были в форме гистограммы, а то, что мы показываем здесь, является огибающей кривой, примерно повторяющей эту гистограмму. Это похоже на диаграмму неопределенности, ею она и является. На самом деле это можно представить в двух обычных формах, как показано ниже:

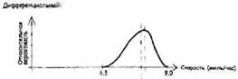
Это распределение прошлых результатов можно рассматривать как представление неопределенности в отношении того, как быстро вы побежите в следующий раз.

Предположим, что ваша скорость является не единственной неопределенностью, влияющей на следующий забег. Предположим, вы решили побежать по дорожке неизвестной длины: по периметру площадки для гольфа. Поскольку вы никогда раньше там не бегали, вы совсем не уверены, сколь длительным будет забег. У вас есть какие-то данные, полученные от Профессиональной ассоциации гольфа, о периметре площадки, из которых следует, что это расстояние может быть от двух до четырех миль, причем наиболее вероятна длина периметра примерно в 2,8 мили. Это тоже можно изобразить как распределение:

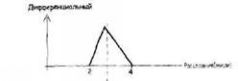
Эти данные более «зернистые» из-за недостаточного их количества.

Итак, сколько займет ваш следующий забег? Вы помните, что время – это расстояние, деленное на скорость (мили расстояния, поделенные на мили/час). Если расстояние и скорость были бы фиксированными величинами, то нам предстояло бы элементарное арифметическое действие, но в данном случае, оба параметра являются неопределенными, меняющимися в рамках определенного диапазона. Это обеспечивает наличие неопределенности также и в результате:

В целях выведения результирующей кривой, составленной из двух входных кривых, нам понадобилось бы использовать метод из области интегрального исчисления. Но такая «крутая» математика непозволительна в этой главе. Что же нам делать?

Вместо того чтобы строить кривую, мы намерены создать ее приближенный вариант путем моделирования ряда последовательных забегов. Для этого нам понадобится построить инструмент, который даст ряд выборочных данных из неопределенности любого вида и в то же время гарантирует соблюдение формы этой неопределенности по времени. Такой инструмент в применении к диаграмме скорости будет выглядеть так:

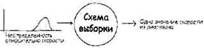
Если бы вы сами осуществляли механизм выборки в этом случае, как бы вы действовали дальше? Первую точку выбрать легко: смотрите на переход от минимума к максимуму и берете любую точку где-то посередине между ними. Кто оспорит ваше решение, на каком бы числе вы ни остановили свой выбор? Но если это нужно проделать больше одного раза, требование «соблюдать форму неопределенности во времени» заставляет задуматься. Как выбрать ряд данных с соблюдением такого же разброса вероятностей, как показан на исходной диаграмме неопределенности?

Как бы вы это ни сделали, фигура из выбранных точек должна, в конечном счете, повторять изначальную диаграмму неопределенности. Чтобы проверить себя, вы можете собрать свои результаты за некоторый период времени, рассортированные по удобным группам, и использовать их для построения гистограммы своих выбранных результатов. Если вы правильно рассчитали процесс выборки, последовательные гистограммы (для все большего и большего числа элементов выборки) могли бы выглядеть так:

В итоге, когда вы наберете пару сотен точек, огибающая вашей гистограммы будет очень похожа на диаграмму неопределенности, с которой вы начали:

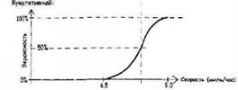
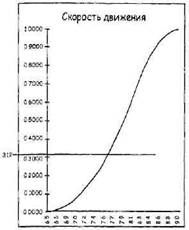
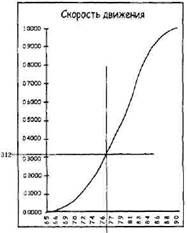
Выборка Монте-Карло – это подход, гарантирующий соблюдение формы наблюдаемой кривой во времени. Механизм выбора Монте-Карло использует данные прошлых наблюдений в форме кумулятивной диаграммы неопределенности вместе с простым генератором случайных чисел для отбора. Если выбрать достаточное количество данных, гистограмма этой выборки начнет аппроксимировать фигуру ваших наблюдаемых данных. Генератор настроен на выдачу случайных чисел между 0 и 1. Вся штука в том, чтобы использовать сгенерированное число для выбора значения на вертикальной оси диаграммы неопределенности и проведения через него горизонтальной линии. Если, например, первое сгенерированное число было 0,312, вы рисуете горизонтальную линию, проходящую через точку 0,312 на вертикальной оси (см. верхний рисунок на следующей странице).

Затем вы проводите вертикальную линию через точку, где ваша горизонталь пересекает кривую. Соответствующая величина на горизонтальной оси – это ваша первая точка выборки (см. нижний рисунок на следующей странице).

Второй рисунок говорит о том, что для первого выборочного забега вокруг площадки можно ожидать скорость 7,66 миль/час. Теперь повторим это, взяв больше случайных чисел, каждое из которых дает выборочное значение скорости. Если достаточно долго продолжать этот процесс и построить из результатов гистограмму, то огибающая гистограммы начнет аппроксимировать диаграмму неопределенности, с которой вы начали (ее дифференциальный вид).

Механизм выборки, построенный на таком простом правиле, можно теперь применить к проблеме бега. Нам понадобится два таких механизма: один для получения данных с диаграммы скорости и другой для получения данных с диаграммы расстояния:

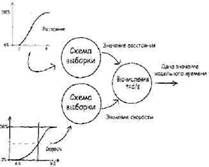
Этот подход позволяет обходиться арифметическими действиями с выборками, вместо интегрального исчисления по кривым. В первый раз, когда вы запускаете этот процесс, он говорит вам, что вы пробежите, скажем, за 33 минуты. Этот результат не так уж и значим – это просто рассчитанное время для случайно выбранных величин из диапазона разброса скорости и расстояния. Но повторение этого процесса снова и снова даст распределение результатов, которые начинают аппроксимировать неопределенности ожидаемого времени забега.

Диаграмма, показанная выше, – это симулятор Монте-Карло для проблемы двойной неопределенности. Он позволяет вам моделировать n случаев проблемы и отображать результаты в форме результирующей диаграммы неопределенности. Вот результат для 100 образцов:

Метод, использованный здесь, не ограничен двумя неопределенностями. Его можно использовать для всего портфеля рисков, грозящих проекту по созданию программного обеспечения.

«RISKOLOGY» – это симулятор Монте-Карло, созданный для менеджера, занимающегося рисками в проекте по разработке программного обеспечения. Это – прямое воплощение механизма выборки по методу Монте-Карло, выраженное в терминах логики электронных таблиц. Мы написали эту программу в Excel, поэтому вам понадобится лицензионная копия программы, чтобы использовать этот инструмент. «RISKOLOGY» идет в комплекте с нашими собственными данными о некоторых рисках, с которыми может столкнуться ваш проект. Вы можете использовать наши данные или заменить их собственными.

Скачайте копию симулятора «RISKOLOGY» с нашего сайта:

Там же можно найти некоторые шаблоны и инструкции по использованию и подгонке симулятора.

Как только вы смоделировали достаточное количество примеров для своего проекта, симулятор обеспечит вам достаточно гладкую результирующую кривую. Эта кривая может показывать совокупные риски, связанные со сроком сдачи вашего проекта или с набором функциональных качеств, которые могут быть готовы к заданному сроку. В терминах управления рисками, результат представляется как диаграмма совокупного риска.

Для незнакомых с управлением рисками, или тех, кому очень сложно понять неопределенность, мы предлагаем воспринимать это как результат моделирования: «Мы прогнали этот проект 500 раз через симулятор, и получили результат, показанный на рисунке».

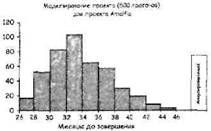
«Как вы видите, это показывает, что мы закончим работу до конца 30-го месяца проекта только в 15% случаев, – говорите вы. – Это не значит, что дата недостижима, она всего лишь имеет высокие риски. На нее можно рассчитывать лишь с 15%-ной уверенностью. Если вам нужна 75%-ная уверенность, вам лучше объявить датой сдачи 40-й месяц».

Наш симулятор «RISKOLOGY» не является единственным вариантом решения этой задачи. Существуют в продаже и другие подобные продукты. Вместо того, чтобы давать здесь прямые указания, мы будем поддерживать список на нашем сайте «RISKOLOGY» (см. URL выше). Там есть описания еще, по крайней мере, двух инструментов – наборов для построения своих собственных симуляторов риска. Эти продукты недороги, и их весьма легко освоить. Далее, как было обещано, мы перейдем к тому, что считаем самыми распространенными ключевыми рисками, с которыми сталкиваются руководители проектов по разработке программного обеспечения.