Книга: Бросай пить! САМОкодирование по системе СОС
Назад: Свобода выбора
Дальше: План-предписание (на первые три года работы над собой с помощью системы СОС)
Приложение
«Закон трех» и «правило девятки»
«Закон трех» представлен на энеаграмме цифрами 3-6-9 (рис. 5). Они определяют координаты равностороннего треугольника, который вписан в окружность этого сакрального геометрического символа. «Закон трех» – фундаментальный закон триединства. С помощью его можно увидеть, например, что по большому счету нет никаких противоречий в объяснении Мироздания со стороны главных мировых религий. Так, в христианстве «закону трех» соответствует то, что верующие люди называют неделимой Троицей: Бог Отец, Бог Сын и Бог Дух Святой. В индуизме это соответствует триумвирату: Богу Шиве, Богу Вишну и Богу Брахме. В буддизме это САТ-ЧИТ-АНАНДА (Сат – Бытие, Чит – Сознание, Ананда – Блаженство).
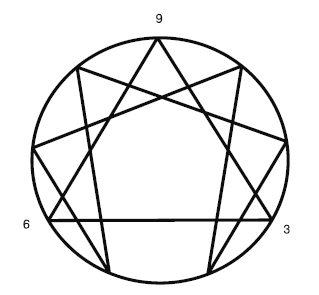
Рис. 5. Закон трех
На уровне человека «закон трех» – это триединство тела, ума и духа. В микромире атомы состоят из трех видов частиц: электронов, нейтронов и позитронов. Прикладное отражение «закона трех» применительно к разработанной мной системе СОС проявляется в триединстве психотехник САМОвнушения, САМОгипноза и САМОкодирования.
«Закон семи» детализирует те частности, которые в общем виде определяются «законом трех». Например, любое явление (или объект), которое нам кажется неподвижным, на самом деле находится в непрерывном движении (как внутреннем, так и внешнем). Представьте себе внешне неподвижный камень у дороги. Но он ведь все-таки движется вместе с планетой Земля. Кроме того, внутри этот камень состоит из атомов. Каждый из них, в свою очередь, чем-то напоминает в миниатюре Солнечную систему. В самом центре атома располагается ядро (мини-солнце), а вокруг него вращаются электроны (мини-планеты). Все это внешнее и внутреннее движение происходит во взаимосвязи с «законом семи».
К сожалению, понять научно-философскую сторону «правила девятки» на простых примерах гораздо сложнее. Тем не менее я упомяну о том, что площадь спины у человека с правильной фигурой (гармонично сложенного) равна площади его девяти ладоней. Девять ладоней умещается на его груди и животе, передняя и задняя часть каждой ноги эквивалентна опять же площади его девяти ладоней. На основе этого алгоритма умеющие философски мыслить люди легко смогут найти и другие схожие примеры. Главное – дать ему соответствующую философскую интерпретацию. Для тех же читателей, кому «глубины философской мистики» чужды по духу, я просто покажу ту занимательную арифметическую закономерность, которую «вытворяет» на энеаграмме цифра 9 (рис. 6).
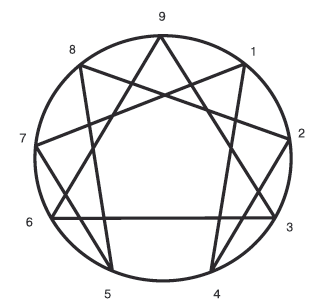
Рис. 6. Энеаграмма
Смотрите.
Если умножить 9 на 9, то результат (81) будет показан цифрой 8 на левой стороне и цифрой 1 на правой стороне круга.
Дальнейшие произведения 9 на 8 и 9 на 7 будут также симметрично разделены на десятки и единицы. В первом случае (72) цифра 7 будет показана на левой стороне и цифрой 2 на правой стороне энеаграммы. Во втором случае искомое произведение (63) будет представлено цифрами 6 и 3.
Начиная с 5 (9 х 5 = 45) порядок становится обратным. Цифры, изображающие единицы (в данном случае 5), оказываются на левой стороне круга, а изображающие десятки (4) – на правой. Смотрите дальше! Если умножить 9 на 4, то это даст в правой части цифру 3, а в левой – симметричную ей 6 (36). Трижды девять будет представлено числом 27 (2 – на правой стороне и 7 – на левой). Наконец, произведение 9 и 2 дает число обратное 81, то есть 18.
Не менее занимательны метаморфозы девятки и в случае использования так называемого пифагорейского сложения. Его называют так в честь древнегреческого мудреца Пифагора. Для тех, кто никогда раньше не слышал о пифагорейском сложении, объясняю его правила. В соответствии с ними любое многозначное число путем сложения составляющих его цифр низводится к одинарному числу. Уяснив это, давайте сначала определим сумму всех чисел на окружности энеаграммы (1+2+3+4+5+6+7+8+ + 9 = 45). Затем полученную сумму низведем с помощью сложения составляющих его цифр к одинарному числу (4 + 5 = 9).
Это будет первая девятка. Аналогичное действие проделаем и с цифрами, которые расположены у вершины треугольника. Они дадут вторую девятку (3 + 6 + 9 = 18; 1 + 8 = 9). Третья девятка получается в процессе сложения всех «незадействованных» треугольником цифр (1+4 + 2 + 8 + 5 + 7 = 27;2 + 7 = 9). К трем пифагорейским девяткам при желании можно добавить и четыре девятки, которые получаются от простого сложения симметричных цифр на окружности энеаграммы. В таком случае мы опять же сталкиваемся с проявлением «закона семи». Смотрите: четвертая девятка (8 + 1 = 9), пятая девятка (7 + 2 = 9), шестая девятка (6 + 3 = 9), седьмая девятка (4 + 5 = 9).
Назад: Свобода выбора
Дальше: План-предписание (на первые три года работы над собой с помощью системы СОС)

