Пусть луч света проникает в сферическую каплю дождя в некоторой точке P на ее поверхности, образуя угол i с нормалью (перпендикуляром) к ее поверхности в этой точке. Если бы преломления света не было, луч продолжал бы идти дальше сквозь каплю по прямой. В этом случае радиус, проведенный из центра капли C к точке Q, лежащей на этой прямой в том месте, где она наиболее близко пролегает к центру капли, образовывал бы с лучом прямой угол, поэтому треугольник PCQ был бы прямоугольным с гипотенузой, равной радиусу капли R, и углом при точке P, равным i (см. рис. 22а). Определим прицельный параметр b как расстояние наибольшего тесного сближения непреломленного луча с центром капли, то есть катетом CQ в этом треугольнике, который по правилам элементарной тригонометрии равен:

С точки зрения положения точки входа в каплю отдельные лучи света можно одинаково хорошо охарактеризовать присущим им отношением b/R, как делал Декарт, или же по значению угла падения i.

В силу явления преломления луч на самом деле войдет внутрь капли под углом r к перпендикуляру к поверхности, значение которого определяется законом преломления:

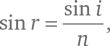
где n ≈ 4/3 – отношение скорости света в воздухе к скорости света в воде. Луч пересечет толщу капли и достигнет поверхности с обратной стороны в точке P’. Поскольку расстояния между центром C и обеими точками P и P’ одинаковы и равны радиусу капли R, треугольник с вершинами C, P и P’ является равнобедренным, поэтому углы между направлением луча и перпендикулярами к поверхности в точках P и P’ должны быть одинаковы, то есть и тот и другой равны r. Часть света отразится в точке P’ от внутренней поверхности капли: по закону отражения угол между отраженным лучом и перпендикуляром к поверхности в ней будет опять же равен r. Затем отраженный луч снова пересечет толщу капли и достигнет ее передней поверхности в точке P’’, снова образуя с поверхностью угол r.

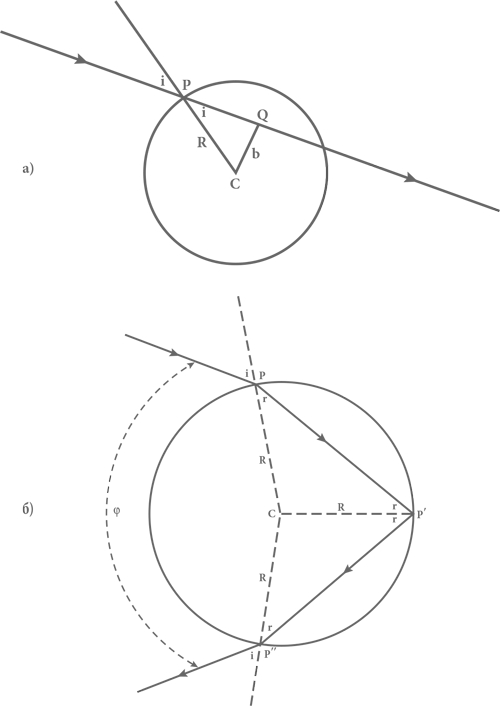
Рис. 22. Путь солнечного луча внутри сферической дождевой капли. Луч обозначен сплошными отрезками с указывающими направление стрелками: он входит внутрь капли в точке P под углом i к перпендикуляру к поверхности: а) путь луча, если бы явления преломления не было: луч в этом случае приближается к центру капли C в точке Q; б) луч преломляется, входя в каплю в точке P, отражается от задней поверхности капли в точке P’ и снова подвергается преломлению в момент выхода из капли в точке P’’. Пунктирные линии проведены из центра капли C к точкам контакта луча с поверхностью капли.

Часть света затем покидает каплю, и по закону преломления угол между выходящим наружу лучом и перпендикуляром к поверхности в точке P’’ будет равен исходному углу падения i (см. рис. 22 – здесь показана схема следования луча в плоскости, проходящей через падающий луч, центр капли и наблюдателя. Только те лучи, которые встречаются с каплей, находясь в этой плоскости, имеют возможность достигнуть наблюдателя).

По мере всей этой серии поворотов луч света отклонится в сторону центра капли на угол i – r дважды – в моменты входа в каплю и выхода из нее, и на угол 180° – 2r при отражении от ее задней поверхности, и значит, полный угол поворота луча составит:

Если бы луч возвращался из капли в направлении, точно противоположном тому, в котором вошел (это происходит в случае, когда i = r = 0), этот угол составил бы 180°, а начальное и конечное направления луча были бы параллельны, поэтому действительный угол φ между ними равен:

Можно выразить r как функцию от i, вот так:

где для любого аргумента x функция arcsin x – это угол (обычно принимаемый в промежутке от –90° до +90°), синус которого равен x. Численный расчет для показателя n = 4/3, который нам встречается в главе 13, показывает, что φ возрастает от нуля при i = 0 до максимального значения при 42° и затем снижается примерно до 14° при i = 90°. График зависимости φ от i горизонтален в своей точке максимума, поэтому большая часть света выходит из капли, подвергаясь отклонению на полный угол, близкий к 42°.

Если мы посмотрим на облачное небо, повернувшись к солнечным лучам спиной, то увидим свет, приходящий к нам под углом 42° между нашим лучом зрения и световыми лучами от солнца. Совокупность этих направлений формирует дугу, которая для нас обычно поднимается в небо из одной точки горизонта и затем опускается к земле в другой. Поскольку коэффициент преломления n слегка варьируется в зависимости от цвета преломляемого луча, для лучей различного цвета углы отклонения φ тоже слегка отличаются, поэтому мы видим дугу, образованную чередованием полос разного цвета. Это и есть радуга.

Нетрудно вывести аналитическую формулу, дающую максимальное значение φ для любого коэффициента преломления n. Чтобы найти максимум φ, примем во внимание тот факт, что точке максимума соответствует такое значение угла падения i, при котором график зависимости φ от i горизонтален, а это означает, что ничтожно малое изменение δφ угла φ, происходящее вследствие ничтожно малого изменения δi угла i, равняется нулю с точностью до первого порядка величины δi. Чтобы использовать это условие, применим табличную формулу из курса дифференциального исчисления, согласно которой при ничтожно малом изменении δх аргумента x изменение arcsin x равно:

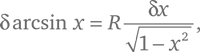
где, если arcsin x измеряется в градусах, R = 360°/2π. Таким образом, когда угол падения изменяется на величину δi, угол отклонения меняется на:

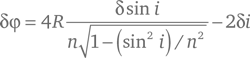
или, поскольку δ sin i = cos i δi/R,

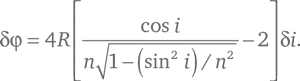
Таким образом, условие максимального значения φ таково, что:

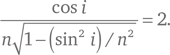
Возведя обе части в квадрат и используя правило cos²i = 1 − sin²i (которое является следствием из теоремы Пифагора), мы можем найти из этого выражения значение для sin i:

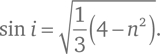
При этом значении угла падения угол φ максимален:

При n = 4/3 максимальный угол отклонения φ достигается при значении b/R = sin i = 0,86, для которого i = 59,4°, r = 40,2° и φ_max = 42,0°.