Герон Александрийский сформулировал закон отражения световых лучей так: угол наклона отраженного луча равен углу наклона падающего. Он исходил из предположения, что путь луча света от объекта к поверхности зеркала и затем к наблюдателю должен быть как можно короче. Точно так же он мог положить в основу и правило о том, что путь луча должен занимать самое короткое время, поскольку время, нужное свету, чтобы преодолеть заданное расстояние, равно частному от деления этого расстояния на скорость света, а в процессе отражения скорость света не изменяется. Однако, когда наблюдается явление преломления, свет проходит сквозь границу двух сред (например, воздуха и стекла), в которых его скорость различна, и приходится рассматривать разницу между понятиями кратчайшего пути и наименьшего времени. Один только факт, что луч света меняет направление на границе сред, говорит о том, что преломленный свет не следует по самому короткому пути в этом случае – прямой линии. Зато, как доказал Ферма, истинный закон преломления света можно вывести, предполагая, что свет стремится затратить как можно меньше времени, чтобы достигнуть цели.

Чтобы получить такой результат, допустим, что свет проходит от точки P_A в среде A, где скорость света равна v_A, к точке P_B в среде B, в которой скорость света равна v_B. Для простоты описания задачи предположим, что поверхность границы раздела сред горизонтальна. Обозначим углы между направлениями лучей света в первой и второй средах и вертикалью i и r соответственно. Если точки P_A и P_B находятся на соответствующих вертикальных расстояниях d_A и b_B от границы раздела, то горизонтальные промежутки между этими точками и той точкой, где луч пересекает поверхность, равны, соответственно, d_A tg i и d_B tg r, где символ «tg» обозначает функцию тангенса угла, отношения длины противолежащего катета к длине прилежащего катета в прямоугольном треугольнике (см. рис. 21). Хотя мы не фиксируем заранее эти два расстояния, их сумма нам известна – это горизонтальное расстояние L между точками P_A и P_B:

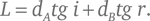
Чтобы вычислить время t, которое требуется свету для преодоления пути из P_A в P_B, обратим внимание, что пройденное им расстояние в средах A и B равняется d_A/cos i и d_B/cos r, соответственно, где «cos» – обозначение функции косинуса угла, отношения длины прилежащего к углу катета к гипотенузе в прямоугольном треугольнике. Время равно расстоянию, деленному на скорость, поэтому полное время будет таково:

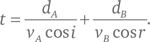
Нам необходимо найти общую зависимость между углами i и r (не включающую параметры L, d_A или d_B), которая удовлетворяет условиям: угол i таков, что общее время t минимально, а величина r связана с величиной i таким образом, что L остается фиксированным. Для этого введем в рассмотрение δi, ничтожно малое изменение δ (дельта) угла падения луча i. Так как горизонтальное расстояние между P_A и P_B постоянно, при изменении угла i на δi угол преломления r также должен измениться, допустим, на величину δr, при условии сохранения расстояния L. Также в точке минимума функции времени t в зависимости от угла i график этой функции должен иметь горизонтальный участок, поскольку, если t в какой-то точке увеличивается или уменьшается, значит, его минимальное значение соответствует какому-то другому значению аргумента i, где сама функция t меньше. Это означает, что изменение t, вызванное ничтожно малым изменением угла δi, обращается в ноль, по крайней мере с точностью до первого порядка величины δi.

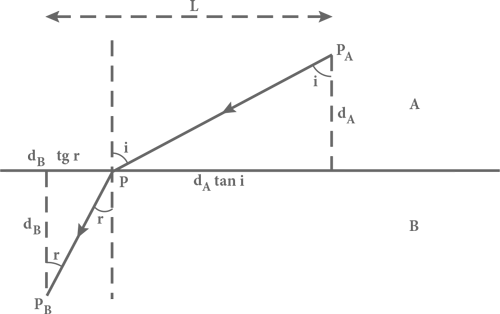
Рис. 21. Путь луча света, испытывающего преломление. Горизонтальной линией отмечена граница двух прозрачных сред A и B, в которых свет имеет различные скорости v_A и v_B. Углы i и r измеряются между направлениями светового луча и вертикальной штриховой линией, обозначающей перпендикуляр к границе раздела сред. Сплошная линия со стрелками отмечает путь следования луча из точки P_A в среде A до точки P на границе раздела сред и затем до точки P_B в толще среды B.

Поэтому, чтобы найти путь, для прохождения которого свету требуется наименьшее время, мы можем ввести условие: при одновременном изменении i и r изменения δL и δt должны оставаться нулевыми с точностью до первого порядка величин δi и δr.

Чтобы удовлетворить ему, нам необходимо взять пару стандартных формул дифференциального исчисления для бесконечно малых изменений значений функций δ tg θ (тета) и δ (1/cos θ), которые получаются, когда мы изменяем угол-аргумент θ на бесконечно малую величину δθ:

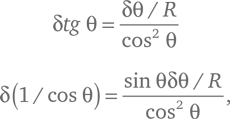
где R = 360°/2π = 57,293…° в случае, когда θ измеряется в градусах (это угол размером в один радиан. При измерении углов в радианах R = 1). По этим формулам мы находим изменения L и t в случае, когда мы меняем углы i и r на бесконечно малые величины δi и δr:

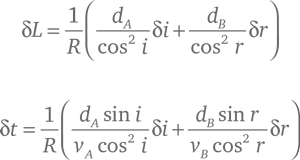
Заданное условие δL = 0 говорит нам, что

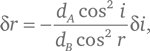
поэтому:

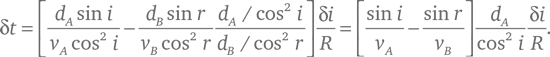
Полученное выражение приравнивается к нулю, если удовлетворяется равенство

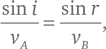
или, иначе говоря,

причем показатель преломления n получается из отношения скоростей, не зависящего от углов:

Это и есть истинный закон преломления света, в котором формула для показателя преломления n верна.