Как правило, посмотреть вдаль нам мешают стоящие недалеко от нас деревья, дома или другие предметы. Стоя на вершине холма в ясный день, мы можем видеть намного дальше, но пределом видимости все равно будет линия горизонта, предметы позади которой мы не видим, потому что их от нас закрывает сама Земля. Арабский астроном аль-Бируни описал хитроумный метод, как, используя это хорошо знакомое всем явление, вычислить радиус Земли, измерив лишь одну линейную величину – высоту горы.

Пусть наблюдатель в точке O вершины горы может видеть самую дальнюю точку H на поверхности Земли, в которой луч его зрения касается земного шара (см. рис. 10).

Этот луч зрения расположен под прямым углом к радиусу, соединяющему точку H с центром Земли C, поэтому треугольник OCH является прямоугольным. Луч зрения пролегает ниже горизонтальной плоскости на некоторый угол θ, который мал за счет того, что Земля большая и линия горизонта находится далеко от наблюдателя. Угол между тем же лучом зрения и вертикальным направлением вниз в точке расположения наблюдателя равен 90° – θ, а значит, поскольку сумма углов любого треугольника равна 180°, острый угол треугольника, прилежащий к центру Земли, равняется 180° − 90° − (90° − θ) = θ. Прилежащий ему катет CH имеет длину, равную радиусу Земли r, а длина гипотенузы треугольника CO есть сумма радиуса Земли r и высоты горы h. По определению, косинус угла прямоугольного треугольника есть отношение длины прилежащего катета к длине гипотенузы, поэтому здесь

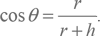
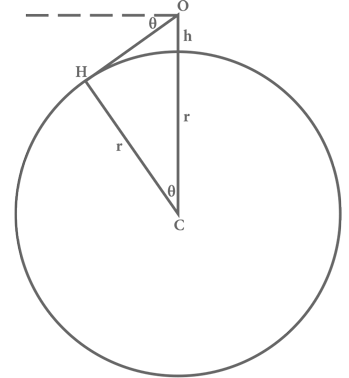
Рис. 10. Примененный аль-Бируни метод определения радиуса Земли путем измерения горизонта. O – наблюдатель на вершине возвышенности высотой h. H – линия горизонта с его точки зрения. Отрезок OH является касательной к поверхности Земли в точке h и, значит, образует прямой угол с радиусом, проведенным из центра Земли C в точку H.

Чтобы вывести из этого уравнения r, обратим внимание, что, если перевернуть обе части, получается равенство 1 + h/r = 1/cos θ. Если теперь вычесть из левой и правой части единицу и снова их перевернуть, то мы получим:

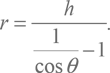
К примеру, наблюдая горизонт на горе в Индии, аль-Бируни нашел, что θ = 34’. Косинус этого угла cos θ = 0,999951092, а 1/cos θ – 1 = 0,0000489. Значит,

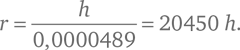
Согласно аль-Бируни, высота этой горы составляла 652,055 локтя (это число дано с точностью, намного превышающей доступную ему точность измерений), что дает результат r = 13,3 млн локтей, хотя он сам приводит число 12,8 млн локтей. В чем именно аль-Бируни ошибся, мне неизвестно.