Раздел современной математики, который называется тригонометрией, изучаемый сейчас в школах и высших учебных заведениях, мог бы здорово помочь античным математикам и астрономам. Тригонометрия учит, каким образом, зная любой из углов прямоугольного треугольника, кроме прямого, вычислить соотношения всех его сторон. Например, результат деления длины катета, противолежащего данному углу, на длину гипотенузы является значением функции под названием «синус угла». Это число можно найти в математических таблицах или рассчитать на калькуляторе, если ввести значение угла и нажать кнопку «sin». В том же треугольнике отношение прилежащего к тому же углу катета к гипотенузе называется косинусом угла, а противолежащего катета к прилежащему – его же тангенсом, но нам сейчас достаточно поговорить о синусах. Хотя синус ни разу не упоминается в трудах математиков эпохи эллинизма, в «Альмагесте» Птолемея встречается связанная с ним функция, которая называется хордой угла.

Чтобы дать определение хорде угла θ (тета), нарисуем окружность радиусом 1 (в любых удобных для вас единицах измерения длины) и проведем из ее центра два луча, разделенные углом θ. Хордой угла будет в этом случае называться отрезок, соединяющий точки пересечения этих двух радиусов с окружностью (см. рис. 9). В «Алмагесте» приводится таблица хорд в вавилонской шестидесятеричной системе счисления, в которой углы выражены в градусах, в промежутке от 1/2° до 180°. Например, для угла 45° в таблице дано значение хорды 45 55 19, что можно перевести в привычный нам вид таким образом:

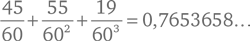
В то же время истинное значение равняется 0,7653669…

Хорды естественным образом применяются в астрономии. Если мы представим себе, что звезды расположены на сфере единичного радиуса, центр которой совпадает с центром Земли, то, если две звезды разделены угловым расстоянием θ, воображаемый отрезок, соединяющий эти две звезды на сфере по прямой, будет иметь длину хорды угла θ.

Рис. 9. Хорда угла θ. Начерченная здесь окружность имеет радиус, равный 1. Два изображенных сплошной линией радиуса образуют угол θ. Горизонтальный отрезок проведен между точками пересечения радиусов с окружностью. Его длина равна хорде этого угла.

Чтобы понять, какое отношение хорды имеют к тригонометрии, вернемся к геометрическому определению хорды угла θ и проведем перпендикуляр (штриховая линия на рис. 9) к хорде из центра окружности, который делит хорду точно пополам. Мы получим два прямоугольных треугольника, у каждого из которых угол, прилегающий к центру окружности, равен θ/2, а противолежащий ему катет в два раза короче хорды. Гипотенузы обоих треугольников равны радиусу окружности, который мы принимаем равным 1, поэтому синус угла θ/2 – в математической записи sin θ/2 – есть половина хорды угла θ, или:

Поэтому любое вычисление с использованием синусов можно выполнить и при помощи хорд, хотя и с несколько меньшим удобством.