Открытие закона отражения световых лучей Героном Александрийским явилось одним из самых ранних примеров того, как закон физики выводится средствами математики из другого, более общего принципа. Допустим, наблюдатель в точке A видит отражение в зеркале объекта в точке B. Если наблюдатель видит изображение в точке P на зеркале, то световой луч в таком случае проделал путь из точки B в точку P, а затем в точку A (Герон, вероятно, сказал бы, что луч прошел от наблюдателя из точки A к зеркалу, а затем к объекту в точке B, как если бы глаз таким образом дотронулся до объекта, но на ход наших рассуждений это не повлияет). Задача заключается в следующем: где именно на зеркале находится точка P?

Чтобы ответить на этот вопрос, Герон предположил, что свет всегда следует кратчайшим путем. В случае отражения это означает, что точка P должна быть расположена так, чтобы общая длина пути из B в P, а затем в A была бы наименьшей среди всех возможных путей из двух прямолинейных отрезков между точкой B, зеркалом и точкой A. Отсюда он заключил, что угол θ_п (тета_п) между зеркалом и падающим на него лучом света (отрезком между точкой B и зеркалом) равен углу θ_о между зеркалом и отраженным лучом (отрезком между зеркалом и точкой A).

Доказательство правила о равных углах падения и отражения таково. Начертим прямую, перпендикулярную поверхности зеркала, проходящую через точку B и точку B′, которая находится на таком же расстоянии позади зеркала, как B перед ним (см. рис. 3). Допустим, что эта прямая пересекает зеркало в точке C. Катеты B′C и CP прямоугольного треугольника B′CP имеют ту же длину, что и катеты BC и CP в треугольнике BCP, поэтому гипотенузы B′P и BP этих двух прямоугольных треугольников также должны быть равны. Значит, полное расстояние, которое луч света проходит из B в P, а потом в A, такое же, как если бы он проходил из B′ в P, а затем в A. Кратчайшее расстояние между точками B′ и A – это отрезок прямой, а значит, кратчайший путь между реальным объектом и наблюдателем – такой, при котором точка P лежит на отрезке B′A. В случае пересечения двух прямых линий противолежащие по отношению к точке пересечения углы равны, поэтому угол θ между отрезком B′P и зеркалом равен углу θ_о между отраженным лучом и зеркалом. Но поскольку у прямоугольных треугольников B′CP и BCP все стороны одинаковы, угол θ должен быть также равен углу θ_п между падающим лучом и зеркалом. Таким образом, поскольку и θ_о, и θ_п равны θ, они взаимно равны. Это фундаментальное правило равенства углов падения и отражения определяет положение точки P, которая соответствует изображению объекта в зеркале.

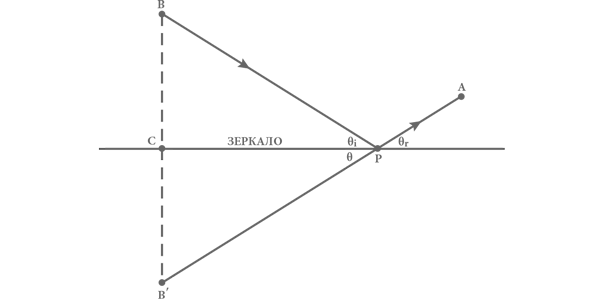
Рис. 3. Доказательство теоремы Герона. Теорема доказывает, что кратчайший путь из объекта B до поверхности зеркала и затем к наблюдателю в точке A таков, что углы θ_п и θ_о равны. Начерченные сплошной линией отрезки помечены стрелками, показывающими направление движения луча света. Штриховая линия – перпендикуляр к поверхности зеркала между точкам B и B’, находящимися на одинаковом расстоянии от зеркала, но по разные стороны от него.