Стратон пронаблюдал, что падающие одна за другой капли одной струи отдаляются друг от друга все больше и больше по мере падения. Из этого факта он заключил, что капли падают ускоренно. Если одна капля в какой-то момент падения оказалась ниже другой, это значит, что первая из них прошла большее расстояние. К тому же, раз капли по мере падения отдаляются, то та из них, которая падает дольше, падает быстрее, демонстрируя ускоренное падение. Хотя Стратон не знал этого, ускорение в этом случае постоянно, и, как мы увидим, результатом является то, что разрывы между каплями в цепочке капель, в которую превращается струя, возрастают пропорционально времени падения.

Как упоминалось в техническом замечании 6, если сопротивлением воздуха можно пренебречь, то ускорение падающего тела равно g, ускорению свободного падения, которое вблизи поверхности Земли равно 9,8 м/с за секунду. Если в начальный момент падения тело находилось в покое, то по истечении интервала времени τ (тау) его скорость будет равна gτ. Таким образом, если две одинаковые капли 1 и 2 срываются со среза одного и того же сливного лотка в различные моменты времени t₁ и t₂, то в какой-то более поздний момент времени они приобретут скорости v₁ = g (t – t₁) и v₂ = g (t – t₂) соответственно. Разность их скоростей, таким образом, составит:

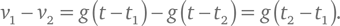
Несмотря на то что и v₁, и v₂ растут со временем, их разность не зависит от конкретного момента t, поэтому расстояние s между двумя каплями просто увеличивается прямо пропорционально времени:

Например, если вторая капля срывается со среза сливного лотка на одну десятую долю секунды позже первой, то половину секунды спустя две капли окажутся на расстоянии 9,8 × 1/2 × 1/10 = 0,49 м одна от другой.