Ни в чем не ужасен, плох во всем

Книга: Много цифр. Анализ больших данных при помощи Excel

Назад: Захватывающее дело Хадлум против Хадлум

В этом разделе вам придется представить себя в роли управляющего большим центром поддержки клиентов. Каждый звонок, электронное письмо или сообщение в чате от покупателя создает жетон. Один работник службы поддержки должен обрабатывать не меньше 140 жетонов в день. В конце каждого диалога клиенту дается возможность оценить работника по пятибалльной шкале. Сотрудники должны поддерживать свой рейтинг не ниже 2, иначе их уволят.

Высокие стандарты!

Компания также следит за множеством других показателей своих работников. Сколько раз они опоздали в этом году? Сколько у них было ночных смен и смен, приходящихся на выходные? Сколько они брали больничных и какое количество из них приходилось на пятницу? Компания знает, сколько часов сотрудник тратит на внутренние обучающие курсы (она оплачивает до 40 часов) и сколько раз он оставлял запрос на замену смен или был добрым самаритянином и шел навстречу просьбам коллег.

Все эти данные на каждого из 400 сотрудников службы поддержки содержатся у вас в таблице. Вопрос в том, кто из них является выбросом и какие выводы о его работе можно сделать? Есть ли плохиши, проскользнувшие между теми, кто не подходит по требованиям жетона, и минимальным клиентским рейтингом? Возможно, выбросы подскажут, как сформулировать новые, более эффективные инструкции.

Открыв электронную таблицу для этого раздела главы (SupportCenter.xlsx можно скачать на сайте книги ), вы найдете все эти данные слежки за служащими во вкладке SupportPersonnel (рис. 9–5).

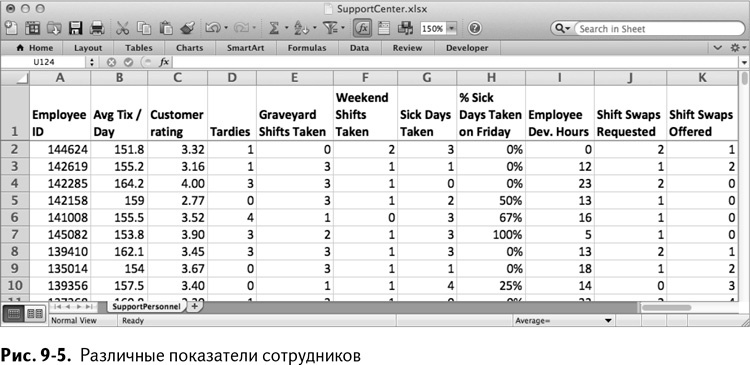
Подготовка данных к отображению на графе

С этими данными есть одна проблема. Нельзя измерить расстояние между сотрудниками, чтобы выяснить, кто находится «за пределами», потому что каждый столбец имеет свои единицы измерения. Что значит разница, равная 5, между двумя работниками в их среднем количестве жетонов относительно разницы в 0,2 в клиентском рейтинге? Нужно стандартизировать каждый столбец, чтобы значения были ближе к единому центру и распределению.

Способ стандартизации столбцов данных таков:

• вычесть среднее значение столбца из каждого наблюдения;

• разделить каждое наблюдение на стандартное отклонение столбца.

Для нормально распределенных данных центром является 0 (что дает нулевое среднее), а стандартное отклонение равно 1. Нормальное распределение с центром в 0 и стандартным отклонением в 1 называется стандартным нормальным распределением.

Стандартизация устойчивыми параметрами

центрированности и шкалы

Начнем с того, что не все данные, которые вам хочется нормализовать, распределены нормально. Вычитание среднего и деление последовательно на стандартное отклонение в любом случае срабатывают. Но выбросы могут испортить среднее значение и расчет стандартного отклонения, поэтому иногда специалисты предпочитают стандартизировать вычитанием более устойчивой статистики центрированности («середины» данных) и последовательным делением на более устойчивые параметры шкалы / статистического распределения (разброс данных).

Вот несколько способов рассчитать центрированность, определяющих одномерные выбросы лучше, чем среднее:

• медиана – просто 50-й персентиль;

• межквантильное среднее – среднее между 25-м и 75-м персентилями;

• тройное среднее – среднее между медианой и межквантильным средним. Оно мне нравится за умное название;

• усеченное среднее – среднее, из которого выкинули N верхних и нижних процентов точек. Такое часто можно встретить на спортивных соревнованиях (например, по гимнастике, где отбрасываются высшие и низшие баллы). Если отбросить по 25 % сверху и снизу и взять среднее от 50 % данных в середине, то получится величина, имеющая свое название – межквартильное среднее (МКС);

• винсоризированное среднее – похоже на усеченное, но вместо отбрасывания слишком большие и слишком маленькие значения заменяются на граничные.

Что касается робустных параметров шкалы, то вот некоторые полезные замены среднеквадратичному отклонению:

• межквартильный размах, с которым вы уже встречались ранее в этой главе. Это просто 75-й персентиль минус 25-й. Можно пользоваться и другими – илями. К примеру, если вычесть 101-й персентиль из 90-го, то получится междецильный размах;

• медиана абсолютного отклонения (МОА). Вычислите медиану данных. Теперь возьмите абсолютное значение разницы каждой точки и медианы. Медианой этих отклонений и будет МОА. Что-то вроде ответа медианы среднеквадратичному отклонению.

Итак, приступим. Вычислите среднее значение и стандартное отклонение каждого столбца внизу листа SupportPersonnel. Первым значением здесь будет среднее количество жетонов за день в ячейке В402, которое можно записать как:

=AVERAGE(B2:B401)

=СРЗНАЧ(B2:B401)

А под ним рассчитайте стандартное отклонение столбца:

=STDEV(B2:B401)

=СТАНДОТКЛОН(B2:B401)

Копируя эти две формулы в столбец К, получаем лист, изображенный на рис. 9–6.

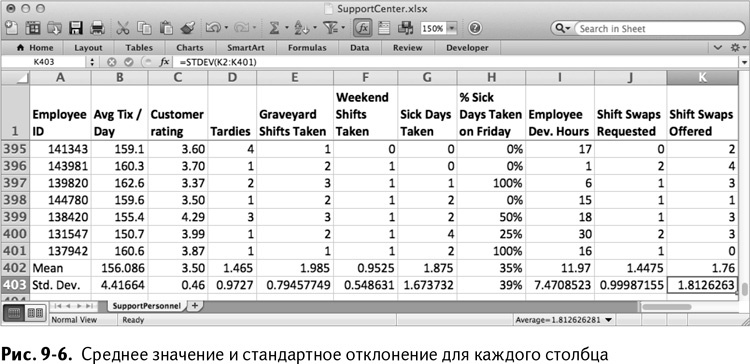
Создайте новый лист, назовите его Standardized. Скопируйте туда названия столбцов из строки 1 и персональные номера работников из столбца А. Нормализацию значений можно начать с ячейки В2 и формулы STANDARDIZE/НОРМАЛИЗАЦИЯ. Эта формула берет исходное значение, центр и величину рассеяния и выдает значения с вычтенным центром, разделенным на рассеяние. Таким образом, в В2 получается:

=STANDARDIZE(SupportPersonnel!B2,SupportPersonnel!B$402,

SupportPersonnel!B$403)

=НОРМАЛИЗАЦИЯ(SupportPersonnel!B2,SupportPersonnel!B$402,

SupportPersonnel!B$403)

Обратите внимание: абсолютные ссылки стоят только на строки со средним и стандартным отклонением, таким образом они остаются на месте при копировании формулы вниз. Однако ее горизонтальные столбцы при копировании будут меняться.

Скопируйте и вставьте В2 слева направо до К2, выделите и кликните правой клавишей, чтобы распространить вычисления до К401. Получается нормализованный набор данных, показанный на рис. 9–7.

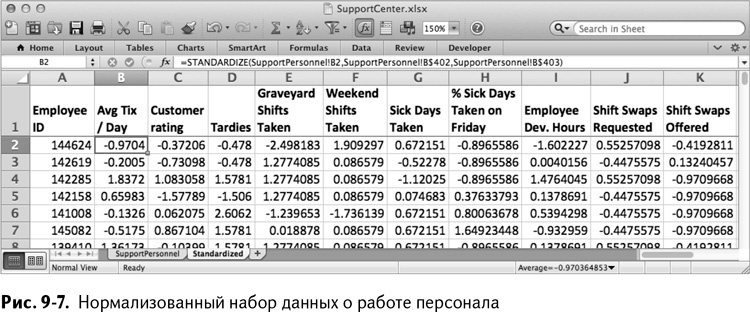
Создаем граф

Граф есть не что иное как ребра и вершины. В нашем случае каждый работник является вершиной, и для начала можно просто провести ребра между ними всеми. Длина ребра – это евклидово расстояние между двумя работниками в их нормализованных данных.

Как вы помните из главы 2, евклидово расстояние (оно же расстояние птичьего полета) между двух точек – это квадратный корень из суммы квадратов разниц каждого столбца для каждого из них.

В новой вкладке Distances создайте матрицу расстояний между сотрудниками точно так же, как в главе 2 – с помощью формулы OFFSET/СМЕЩ.

Пронумеруйте сотрудников от 0 до 399 начиная с А3 вниз и от С1 вправо. (Подсказка: начните печатать 0, 1 и 2 в первых трех ячейках, а затем выделите их и растяните в нужном направлении. Excel заполнит их за вас – он вполне способен с этим справиться.) Рядом с этими числами вставьте персональные номера сотрудников (специальной вставкой с транспонированием столбцов). Так получается пустая матрица, изображенная на рис. 9–8.

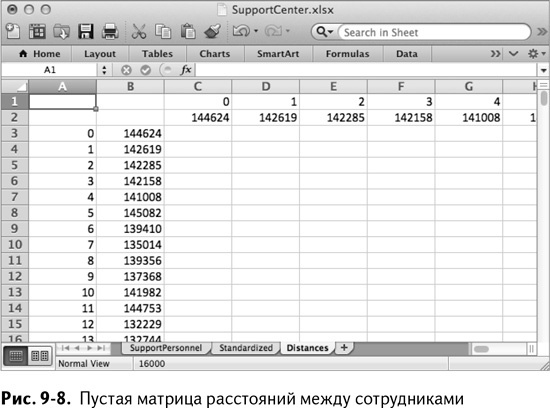
Заполнение матрицы начнем с первой ячейки расстояний, С3. В ней находится расстояние между сотрудником 144624 и им самим.

Для всех расчетов расстояний мы будем пользоваться формулой OFFSET/СМЕЩ, привязанной к первой строке стандартизированных данных сотрудников:

OFFSET(Standardized!$B$2:$K$2, некоторое количество строк, 0 столбцов)

СМЕЩ(Standardized!$B$2:$K$2, некоторое количество строк, 0 столбцов)

Для ячейки С3 Standardized!$B$2:$K$2 – текущая строка работника 144624, так что можно вычислить разницу между этим работником и им самим с помощью формулы смещения:

OFFSET(Standardized!$B$2:$K$2,Distances!$A3,0)-OFFSET

(Standardized!$B$2:$K$2,Distances!C$1,0)

СМЕЩ(Standardized!$B$2:$K$2,Distances!$A3,0) – СМЕЩ

(Standardized!$B$2:$K$2,Distances!C$1,0)

В первой формуле смещения вы двигаете строки с помощью значения в $А3, а во второй – в С$1, чтобы передвинуть OFFSET//СМЕЩ к другому сотруднику. Абсолютные ссылки в этих формулах используются в необходимых местах, поэтому при копировании формулы на весь лист она продолжает считывать значения из столбца А и строки 1.

Этот расчет разности нужно возвести в квадрат, сложить и извлечь квадратный корень, получая таким образом полное евклидово расстояние:

{=SQRT(SUM((OFFSET(Standardized!$B$2:$K$2,Distances!$A3,0)-OFFSET(Standardized!$B$2:$K$2,Distances!C$1,0))^2))}

{=КОРЕНЬ(СУММ((СМЕЩ(Standardized!$B$2:$K$2,Distances!$A3,0) – СМЕЩ(Standardized!$B$2:$K$2,Distances!C$1,0))^2))}

Заметьте, что этот расчет основан на формуле массива из-за отличия строк друг от друга. Поэтому нажмите Ctrl+Shift+Enter (Command+Return в MacOS), и все заработает.

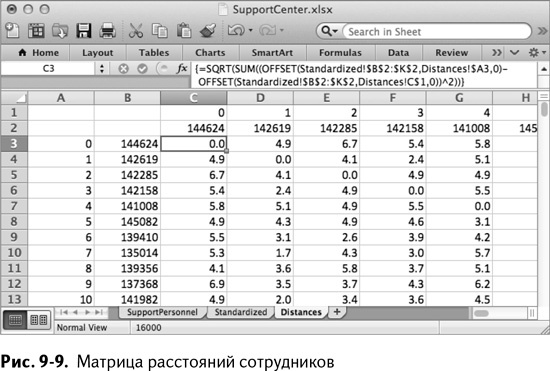
Евклидово расстояние работника 144624 до самого себя действительно равно 0. Раскопируйте эту формулу до OL2, а потом выделите этот промежуток и кликните дважды в нижнем углу, размножив таким образом вычисление до самой OL402. Так получится таблица, показанная на рис. 9–9.

Вот и все! У вас есть граф сотрудников. Можете экспортировать его в Gephi как в главе 5, и взглянуть на то, что получится, но так как у него 16 000 ребер и только 400 вершин, это наверняка жуткая картина.

Подобно тому, как в главе 5 вы конструировали граф r-окрестности из матрицы расстояний, в данной главе мы сфокусируемся лишь на k ближайших соседей каждого сотрудника, чтобы найти выбросы.

Первый шаг – ранжирование, то есть расположение работников согласно расстояниям относительно друг друга. Это приводит нас к первому и основному методу выделения выбросов на графе.

Вычисляем k ближайших соседей

Создайте новый лист под названием Rank. Вставьте персональные номера от А1 вниз и от В1 вправо, чтобы получилась основа для матрицы, как в предыдущей части.

Теперь нужно ранжировать каждого работника в верхней строке в соответствии с его расстоянием до работников в столбце А. Начните с 0 таким образом, чтобы 1 оказывались у действительно других работников, а 0 образовали диагональ графа (так как расстояния до самих себя всегда самые короткие).

Начиная с В2 ранг сотрудника номер 144624 относительно него самого записывается с помощью формулы RANK//РАНГ:

=RANK(Distances!C3,Distances!$C3:$OL3,1)-1

=РАНГ(Distances!C3,Distances!$C3:$OL3,1)-1

Эта –1 в конце и дает нам расстояние до самого себя, равное 0, а не 1. Обратите внимание, что столбцы с С по OL вкладки Distances имеют абсолютные ссылки, что позволяет вам копировать формулу вправо.

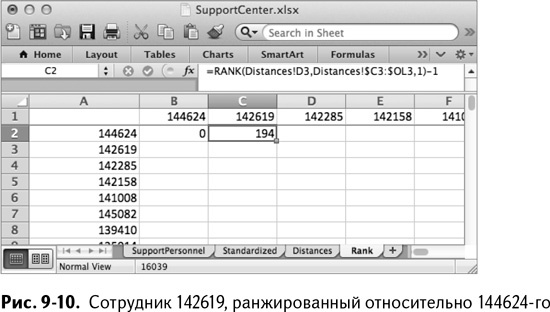
Копируя ее таким образом в первую правую ячейку, С2, вы ранжируете работника 142619 относительно его расстояния до работника 144624:

=RANK(Distances!D3,Distances!$C3:$OL3,1)-1

=РАНГ(Distances!D3,Distances!$C3:$OL3,1)-1

В результате получаем ранг 194 из 400, то есть этих двоих ребят нельзя назвать хорошими друзьями (рис. 9-10).

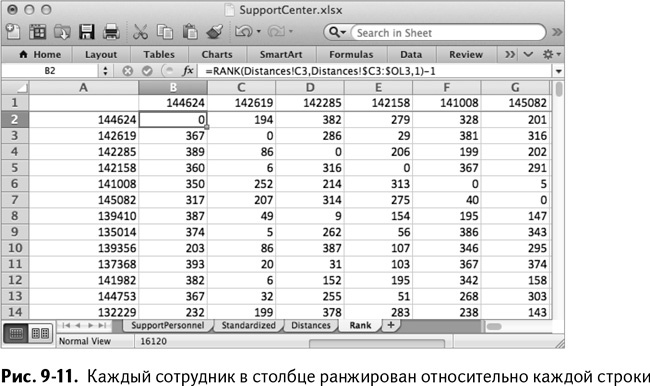
Раскопируйте эту формулу на всю таблицу. У вас получится полная матрица рангов, изображенная на рис. 9-11.

Определение выбросов на графе, метод 1: полустепень захода

Если вы хотите построить граф k ближайших соседей, используя таблицы Distances и Rank, то все, что вам нужно сделать – это удалить все ребра из вкладки Distances (сделать все ячейки пустыми), чей ранг окажется больше, чем k. Для k = 5 вы отбросите все расстояния с рангом 6 и больше.

Что значит выброс в этом контексте? Думаю, он нечасто будет оказываться в числе «ближайших соседей», верно?

Скажем, вы построили граф 5 ближайших соседей, оставив лишь ребра с рангом 5 и меньше. Если просмотреть весь столбец, к примеру столбец В для сотрудника 144624, сколько можно найти его попаданий в первую пятерку всех остальных сотрудников? То есть сколько человек выбирают его одним из 5 ближайших соседей? Немного. На самом деле, я не вижу ни одного такого, кроме него самого с рангом 0 на диагонали, что можно игнорировать.

Как насчет 10 ближайших соседей? Ну, в таком случае сотрудник 139071 в строке 23, оказывается, считает его девятым ближайшим соседом! Это значит, что в графе 5 ближайших соседей работник 144624 имел полустепень захода, равную 0, но в графе 10 ближайших соседей она уже равна 1.

Полустепень захода – это количество ребер, входящих в любую вершину графа. Чем ниже полустепень захода, тем больше вы похожи на выброс, потому что никто не хочет быть вашим соседом.

Внизу столбца В листа Rank вычислите полустепень захода для работника 144624 на графе 5, 10 и 20 ближайших соседей. Сделать это можно с помощью простой формулы COUNTIF/СЧЁТЕСЛИ (вычитая из 1 в случае дистанции до самих себя на диагонали, что игнорируется). Таким образом, чтобы подсчитать, например, полустепень захода для сотрудника 144624 на графе 5 ближайших соседей, нужно в ячейке В402 написать следующее:

=COUNTIF(B2:B401,”<=5”)–1

=СЧЁТЕСЛИ(B2:B401,”<=5”)–1

Точно так же ниже можно рассчитать полустепень захода для сотрудника на графе 10 ближайших соседей:

=COUNTIF(B2:B401,”<=10”)-1

=СЧЁТЕСЛИ(B2:B401,”<=10”)-1

И для 20:

=COUNTIF(B2:B401,”<=20”)-1

=СЧЁТЕСЛИ(B2:B401,”<=20”)-1

Конечно, вы можете выбрать любое k от 1 до числа служащих. Но на этот раз вполне достаточно 5, 10 и 20. Используя меню условного форматирования, выделите ячейки, чье значение равно 0 (что значит отсутствие входящих ребер для этой вершины на графе такого размера). Этот расчет для работника 144624 показан на рис. 9-12.

Выделяя В402:В404, перенесите расчеты вправо до самого столбца ОК. При просмотре результатов видно, что некоторых сотрудников можно считать выбросами на графе 5 ближайших соседей, но они не обязательно окажутся таковыми на графе 10 (если вы определяете выброс как работника с полустепенью 0, при желании можете выбрать другое значение).

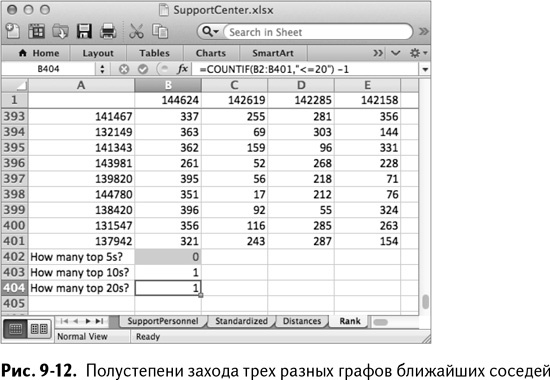
В итоге существуют всего двое сотрудников, у которых даже на графе 20 ближайших соседей нет ни одного входящего ребра. Никто не считает их соседями, даже 20 ближайших. Это довольно далеко!

Персональные номера этих двоих ребят – 137155 и 143406. Переключившись обратно во вкладку SupportPersonnel, можно изучить их получше. Сотрудник 137155 расположен в строке 300 (рис. 9-13). У него большое среднее количество жетонов, высокий клиентский рейтинг и он кажется добрым самаритянином. Он брал много смен в выходные, ночных и семь раз заменял тех, кто просил его об этом. Мило! Вот кто во всех измерениях достаточно исключителен, чтобы не попасть даже в 20 ближайших расстояний до любого другого сотрудника. Удивительно! Наверное, такие работники заслуживают пиццы или чего-то подобного.

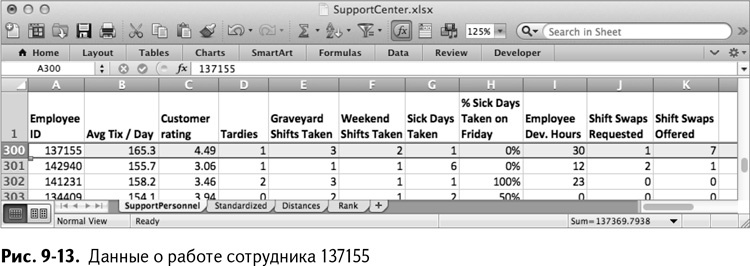
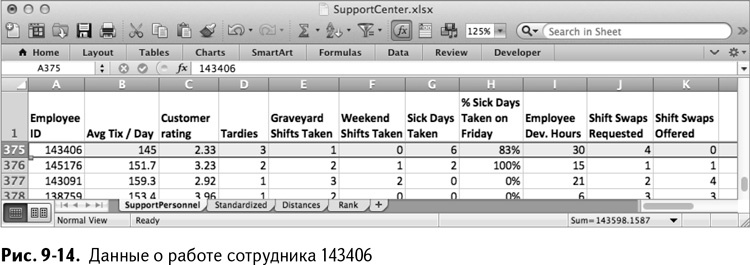
А что насчет второго сотрудника – 143406? Он находится в строке 375 и явно контрастирует с предыдущим служащим (рис. 9-14). Никакие параметры сами по себе не являются достаточными условиями для увольнения, но количество его жетонов на два стандартных отклонения ниже среднего, клиентский рейтинг тоже примерно на пару отклонений ниже распределения. Число опозданий выше среднего и пять из шести больничных приходятся на пятницу. Хммм…

Этот сотрудник посетил массу курсов для персонала, что, конечно, хорошо. Но, возможно, любознательность продиктована тем, что ему просто нравилось отлынивать от обработки жетонов. Быть может, руководству стоило бы дифференцировать занятия для персонала? А еще он просил заменить себя 4 раза, но ни разу не откликнулся на просьбы коллег.

Такие сотрудники остаются на местах благодаря системе. Удовлетворяя минимальным требованиям трудоустройства (заметьте, что здесь тоже никто не переходит границ Тьюки), они плавно скатываются к краям любого распределения.

Определение выбросов на графе, метод 2: нюансы k-расстояния

Одним из недостатков метода, описанного выше, является то, что на конкретном графе k ближайших соседей ты либо получаешь входящее ребро, либо нет. И это означает большие промежутки между теми, кто характеризуется как выброс, и остальными, в зависимости от выбранного k. В этом примере мы пробовали 5, 10 и 20, пока не остались лишь с двумя сотрудниками. Кто из этих двоих является большим выбросом? Понятия не имею! Полустепень захода у обоих 0 даже при k = 20, то есть каким-то образом они все же связаны, не так ли?

Было бы неплохо иметь расчет, привязывающий к работнику длительное значение степени «выбросовости». С помощью следующих двух методов мы будем пытаться сделать именно это. Сначала посмотрим на ранжирование выбросов с помощью величины под названием k-расстояние.

K-расстояние – это расстояние от сотрудника до его k-го соседа.

Прекрасно и просто, но так как результатом является расстояние, а не подсчет, можно ранжировать эту величину. Для удобства создайте новую вкладку в книге под названием K-Distance.

В качестве k у нас будет 5, что значит сбор расстояний всех служащих до их пятых ближайших соседей. Если у меня по соседству живут 5 соседей и я сам, сколько места мы занимаем все вместе? Если мне надо идти в гости к пятому соседу 30 минут, то, похоже, я живу в захолустье.

Так что напишите в А3 «How many employees are in my neighborhood?» («Сколько у меня соседей?»), а в В1 поместите 5. Это ваше значение k.

Начиная с А3, назовите столбцы соответственно персональным номерам работников «Employee ID» и вставьте эти номера во вкладки. Теперь можно начать расчет k-расстояний сотрудника 144624 в ячейке В4.

Так как же вычислить расстояние между 144624 и его пятым ближайшим соседом? Ранг пятого ближайшего сотрудника в строке 2 (строка 144624) вкладки Rank должен быть равен 5. Вы можете просто использовать оператор IF/ЕСЛИ, установив его значение на 1 в векторе из нулей, а затем умножив его на строку расстояний для 144624 вкладки Distances. И, наконец, складываем все вместе.

Таким образом в В4 получается:

{=SUM(IF(Rank!B2:OK2=$B$1,1,0)хDistances!C3:OL3)}

{=СУММА(ЕСЛИ(Rank!B2:OK2=$B$1,1,0)хDistances!C3:OL3)}

Обратите внимание: значение k в В1 зафиксировано абсолютными ссылками, так что можете смело растягивать формулу. А еще она работает для массива целиком – ведь оператор IF/ЕСЛИ проверяет его весь.

Кликните на формуле дважды, чтобы раскопировать ее на весь лист, и примените условное форматирование, выделяя большие расстояния. И снова лидируют два выброса из предыдущего раздела (рис. 9-15).

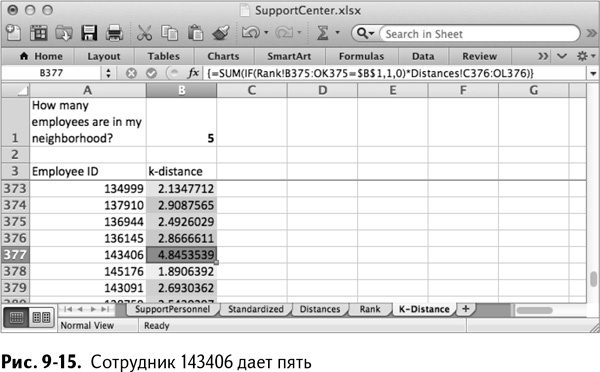
На этот раз есть один небольшой нюанс. По одной этой таблице видно, что плохой работник, 143604, оказывается существенно дальше, чем 137155, и оба эти значения сильно превосходят следующее по величине значение, равное 3,53.

Все же у этого метода есть недостаток, показанный на рис. 9-16. Использование одного k-расстояния дает чувство глобальной принадлежности к выбросам, в чем вы можете убедиться, выделив цветом точки, наиболее отдаленные от своих соседей. Но после знакомства с рисунком 9–16 становится ясно, что хотя треугольная точка – самый что ни на есть выброс, но все же его k-расстояние меньше, чем у некоторых ромбов.

Неужели эти ромбики еще страннее, чем треугольник? Только не для меня!

Дело здесь в том, что треугольник не является глобальным выбросом, потому что он – локальный выброс. Причина, по которой ваши глаза зафиксировали в качестве странного именно его, заключается в том, что он ближе к кластеру кружков. Если бы треугольник оказался среди разбредшихся ромбов, все было бы иначе. Но это не так. Наоборот, похоже, это его «круглые» соседи.

В итоге у нас получается суперсовременная техника под названием факторы локальных выбросов (ФЛВ).

Определение выбросов на графе, метод 3: факторы локальных выбросов – это то, что надо

Как и k-расстояния, факторы локальных выбросов дают по одному «баллу» за каждую точку. Чем больше баллов, тем в большей степени выбросом является точка. Но ФЛВ дает вам нечто немного большее: чем ближе балл к единице, тем более обыкновенна данная точка локально. С ростом балла точка считается все менее типичной и более относящейся к выбросам. В отличие от k-расстояния, подход «единица типична» никак не сказывается на масштабе графа, что действительно круто.

На высоком уровне это работает так: ты являешься выбросом, если k твоих ближайших соседей считают тебя дальше, чем их соседи считают их самих. Алгоритму интересны друзья точек и их друзья. Так он понимает слово «локальный».

Анализируя рис. 9-16, можно понять, что именно делает треугольник выбросом. У него может не быть лучшего k-расстояния, но отношение расстояния треугольника к его ближайшим соседям по сравнению с их расстояниями друг до друга довольно велико (рис. 9-17).

Начнем с достижимости

Перед тем, как свести вместе все факторы локальных выбросов для каждого сотрудника, нужно рассчитать еще одну последовательность чисел – расстояние достижимости.

Расстояние достижимости сотрудником А сотрудника В – это обычное расстояние между ними, пока А не оказывается по соседству с В, то есть удаленным на k-расстояние, которое и превращается в таком случае в расстояние достижимости.

Другими словами, если А попадает в окрестность точки В, вы округляете расстояние от А до В до размера окрестности, а если же нет – то просто оставляете без изменений.

Использование расстояния достижимости вместо обычного расстояния при расчете ФЛВ помогает немного стабилизировать вычисления.

Создайте новый лист под названием Reach-dist и замените расстояния из вкладки Distances новыми расстояниями достижимости.

Первое, что нужно сделать – вставить транспонированные значения из матрицы работников листа K-Distance специальной вставкой в верхнюю часть таблицы слева направо, начиная со строки 3. Получится пустая таблица, изображенная на рис. 9-18.

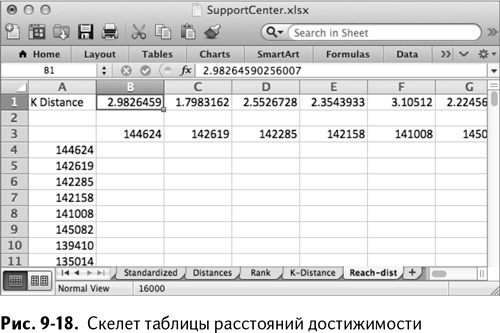
Начиная с ячейки В4 вы будете перебирать расстояния от 144624 до него самого из вкладки Distances (Distances! C3), пока оно не окажется меньше, чем k-расстояние наверху в В1. Это обычная формула MAX/МАКС:

=MAX(B$1,Distances!C3)

=МАКС(B$1,Distances!C3)

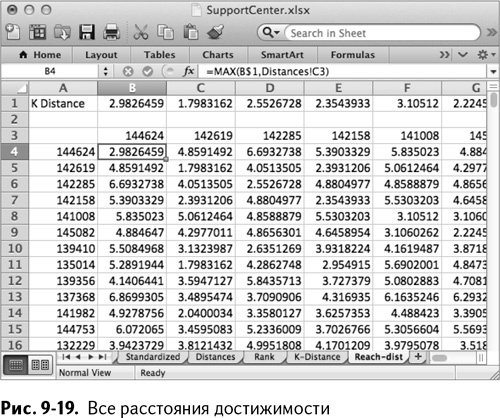
Абсолютная ссылка на k-расстояние позволяет вам копировать формулу на весь лист. Скопировав ее до ОК4, выделите вычисления в строке 4 и кликните на них дважды, чтобы распространить на всю таблицу до строки 403. Таким образом заполняются все расстояния достижимости, как показано на рис. 9-19.

Сводим воедино все факторы локальных выбросов

Теперь все готово к вычислению факторов локальных выбросов для каждого сотрудника. Создайте новую вкладку, назовите ее LOF, а затем вставьте в столбец А персональные номера сотрудников.

Как я упоминал ранее, факторы локальных выбросов характеризуют то, как точка выглядит с точки зрения своих соседей относительно того, как выглядят остальные соседи с такой точки зрения. Если я живу в 30 километрах от города, мои ближайшие соседи могут считать меня деревенщиной, но сами они в то же время считаются среди односельчан членами одного сообщества. Это значит, что локально я в большей степени выброс, чем мои соседи. Нужно запечатлеть этот феномен.

Эти значения держатся на средней достижимости каждого сотрудника его k ближайшими соседями.

Пусть работник 144624 находится у нас в строке 2. Значение k уже установлено на 5. Вопрос в том, каково среднее расстояние достижимости 144624 его пятью ближайшими соседями?

Чтобы его вычислить, выберите вектор из единиц в таблице Rank для пяти сотрудников, ближайших к 144624, и из нулей для кого-нибудь еще (вы делали нечто похожее во вкладке K-Distance). Такой вектор можно создать с помощью оператора IF//ЕСЛИ, собрав всех соседей с высоким рангом, но исключив самого работника:

IF(Rank!B2:OK2<=’K-Distance’!B$1,1,0)*IF(Rank!B2:OK2>0,1,0)

ЕСЛИ(Rank!B2:OK2<=’K-Distance’!B$1,1,0)*ЕСЛИ(Rank!B2:OK2>0,1,0)

Умножьте этот вектор-индикатор на расстояния достижимости 144624, сложите результаты и разделите все на k= 5. В ячейке В2 у вас получится:

=SUM(IF(Rank!B2:OK2<=’K-Distance’!B$1,1,0)*IF(Rank!B2:

OK2>0,1,0)*‘Reach-dist’!B4:OK4)/’K-Distance’!B$1}

=СУММ(ЕСЛИ(Rank!B2:OK2<=’K-Distance’!B$1,1,0)*ЕСЛИ(Rank!B2:

OK2>0,1,0)*‘Reach-dist’!B4:OK4)/’K-Distance’!B$1}

Как только вы вычислили k-расстояние, эта формула становится формулой массива. Распространите ее на всю таблицу, кликнув на ней дважды (рис. 9-20).

Таким образом, в этом столбце отображается то, как выглядит каждый сотрудник с точки зрения пяти своих ближайших соседей.

Фактор локального выброса для сотрудника – это среднее значение отношений расстояний достижимости этого сотрудника, разделенное на средние достижимости каждого из k своих соседей.

Сначала мы выполним расчет ФЛВ для сотрудника 144624 в ячейке С2. Как и в предыдущих расчетах, оператор IF//ЕСЛИ дает нам вектор из единиц для пяти ближайших соседей 144624:

IF(Rank!B2:OK2<=’K-Distance’!B$1,1,0)*IF(Rank!B2:OK2>0,1,0)

ЕСЛИ(Rank!B2:OK2<=’K-Distance’!B$1,1,0)*ЕСЛИ(Rank!B2:OK2>0,1,0)

Затем мы умножаем это на отношение средней достижимости 144624, разделенное на среднюю достижимость каждого из соседей:

IF(Rank!B2:OK2<=’K-Distance’!B$1,1,0)*IF

(Rank!B2:OK2>0,1,0)*B2/TRANSPOSE(B$2:B$401)

ЕСЛИ(Rank!B2:OK2<=’K-Distance’!B$1,1,0)*ЕСЛИ

(Rank!B2:OK2>0,1,0)*B2/ТРАНСП(B$2:B$401)

Обратите внимание: в формуле массива используются фигурные скобки. Нажмите Ctrl+Shift+Enter (Command+Return в MacOS) чтобы получить ФЛВ для 144624.

Результат равен 1,34, что несколько больше единицы. Это значит, что данный сотрудник в некоторой степени является локальным выбросом.

Раскопируйте эту формулу на всю таблицу двойным кликом, а затем проверьте остальных работников. Условное форматирование поможет найти самые значительные выбросы.

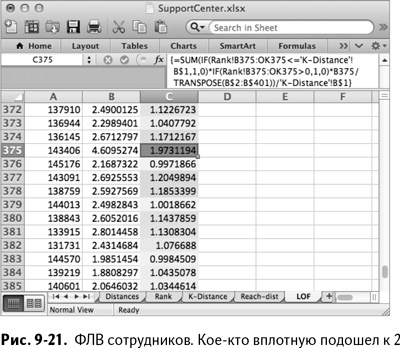
Например, промотав таблицу вниз до конца, вы обнаруживаете, что сотрудник 143406, штатный халтурщик, – самая отдаленная точка с ФЛВ, равным 1,97 (рис. 9-21). Его соседи видят его вдвое дальше, чем другие соседи видят их самих. Это довольно далеко от группы.

Вот и все! Теперь у вас есть по одному значению, соотнесенному с каждым сотрудником, которое ранжирует его как локальный выброс и измеряется независимо от размера графа. Великолепно!

Назад: Захватывающее дело Хадлум против Хадлум

Дальше: Подытожим