Захватывающее дело Хадлум против Хадлум

Книга: Много цифр. Анализ больших данных при помощи Excel

Дальше: Ни в чем не ужасен, плох во всем

Заметка

Электронная таблица “Pregnancy Duration.xlsx”, используемая в этой главе, доступна для скачивания вместе с книгой на сайте издательства . Ниже мы перейдем к таблице побольше, “SupportCenter.xlsx”, доступной по тому же адресу.

Когда-то давно, в 1940-х годах, один британец по имени мистер Хадлум ушел на войну. Энное количество дней спустя (349, если быть точным) его жена, миссис Хадлум, родила. В среднем беременность длится 266 дней. Таким образом получается, что миссис Хадлум носила ребенка лишних 12 недель. Исключительно долгая беременность, не правда ли?

Именно так и утверждала миссис Хадлум.

Но мистер Хадлум тоже был не лыком шит и настаивал, что в деле замешан другой мужчина, с которым миссис Хадлум встречалась в его отсутствие: 349-дневная беременность – аномалия, которую трудно оправдать статистическим распределением продолжительности.

При наличии подобных данных наверняка можно быстренько определить, стоит ли считать выбросом интересный случай миссис Хадлум?

Исследования показали, что продолжительность беременности – величина с более-менее нормальным распределением со средним значением в 266 дней после оплодотворения и стандартным отклонением около 9. Так что можно вычислить значение функции нормального интегрального распределения, упоминавшегося в главе 4, и получить вероятность, меньшую требуемых 349. В Excel это легко сделать с помощью функции NORMDIST/НОРМРАСП:

=NORMDIST(349,266,9,TRUE)

=НОРМРАСП(349,266,9,ИСТИНА)

Эта функция требует выбора интересующего вас случая, его среднего, стандартного распределения и отметки TRUE/ИСТИНА, которая заставит функцию выдать интегральное значение.

Формула все время выдает 1,000, сколько бы знаков после запятой Excel я ни рассчитал. Это значит, что почти все дети, рожденные от настоящего момента до бесконечности, будут рождены на 349-й день или раньше. Вычитаем это значение из 1:

=1-NORMDIST(349,266,9,TRUE)

=1-НОРМРАСП(349,266,9,ИСТИНА)

И получаем, конечно же, 0,000000 насколько хватает глаз. Другими словами, человеческого детеныша практически невозможно вынашивать так долго.

Мы никогда точно не узнаем ответа, но я бы поставил неплохие деньги на то, что миссис Хадлум имела интрижку на стороне. Самое смешное, что суд решил дело в ее пользу, постановив, что такая долгая беременность, хотя и очень маловероятна, но все же возможна.

Границы Тьюки

Концепция того, что выбросы – это маловероятные точки на колоколообразной кривой, методом проб и ошибок привела к границам Тьюки. Их легко проверить и легко программировать. Они используются в статистических пакетах по всему миру для идентификации и удаления сомнительных точек данных из любого ряда, соответствующего нормальной колоколообразной кривой.

Метод Тьюки заключается в следующем:

• Рассчитать 25-й и 75-й персентиль любого ряда данных, в котором вы хотите найти выбросы. Эти значения также называются первым и третьим квартилями. Excel вычисляет их значения с помощью функции PERCENTILE/ПЕРСЕНТИЛЬ.

• Вычесть первый квартиль из третьего – получится мера распределения данных, называемая межквартильным размахом (МР). МР прекрасен своей относительной устойчивостью к экстремальным значениям меры распределения (то есть робустный), в отличие от обычного расчета стандартного распределения, которым вы пользовались в предыдущих главах этой книги.

• Вычесть 1,5 × МР из первого квартиля и получить нижнюю внутреннюю границу. Прибавить 1,5 × МР к третьему квартилю и получить верхнюю внутреннюю границу.

• Точно так же вычесть 3 × МР из первого квартиля, чтобы получить нижнюю внешнюю границу. Прибавить 3 × МР к третьему квартилю, чтобы получить верхнюю внешнюю границу.

• Любое значение, меньшее нижней границы или выше верхней, экстремально. В данных с нормальным распределением вы увидите одну точку на 100 снаружи внутренней границы, и только одну на 500 000 точек за пределами внешней границы.

Применение границ Тьюки в таблице

Я включил таблицу под названием PregnancyDuration.xlsx в файлы, доступные для загрузки на сайте книги, так что вы можете применить этот метод к реальным данным. Открыв ее, вы увидите лист Pregnancies с 1000 наблюдений в столбце А.

Срок беременности миссис Хадлум в 349 дней находится в ячейке А2. В столбец D поместите всю итоговую статистику и границы. Начните с медианы (среднего значения), которая более устойчива как статистика центрированности, чем среднее значение (на которое могут влиять выбросы).

Озаглавьте С1 как Median, а в D1 рассчитайте значение медианы следующим образом:

=PERCENTILE(A2:A1001,0.5)

=ПЕРСЕНТИЛЬ(A2:A1001,0.5)

Это будет 50-й персентиль. Под медианой вычислите первый и третий квартили:

=PERCENTILE(A2:A1001,0.25)

=PERCENTILE(A2:A1001,0.75)

=ПЕРСЕНТИЛЬ(A2:A1001,0.25)

=PERCENTILE(A2:A1001,0.75)

А межквартильный размах – это разница:

=D3-D2

«Приклеивая» 1,5 и 3, умноженные на МР к первому и третьему квартилю соответственно, можно затем вычислить все границы:

=D2–1.5*D4

=D3+1.5*D4

=D2–3*D4

=D3+3*D4

Если вставить названия всех величин, получится таблица, показанная на рис. 9–1.

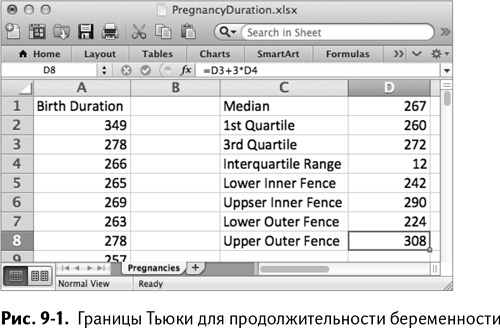
Применив к таблице условное форматирование, можно посмотреть, кто же выпадает за образованные границы. Чтобы выделить экстремальные значения, выберите «Условное форматирование» из домашней вкладки меню, затем нажмите «Правила выделения ячеек» и «Меньше, чем», как показано на рис. 9–2.

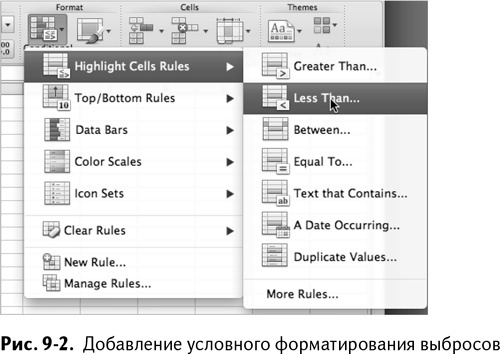
Определяя нижнюю внутреннюю границу, не стесняйтесь выбирать яркий цвет, который вам по душе (я выбрал желтую заливку для внутренних границ и красную для внешних, потому что люблю светофоры). Таким же образом отформатируйте три остальные границы (если у вас Excel 2011 для MacOS, используйте правило «Форматировать только значения, которые находятся выше или ниже заданных», чтобы добавить 2 правила вместо 4).

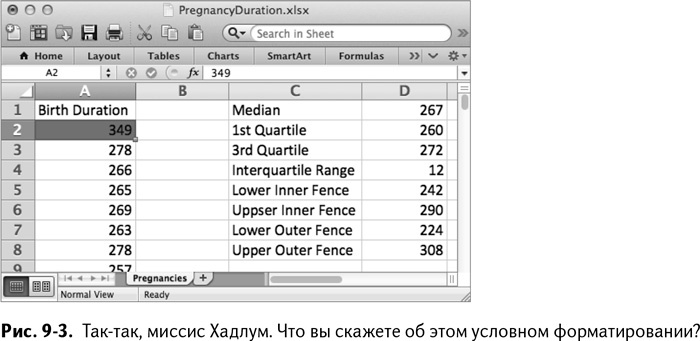
Как показано на рис. 9–3, миссис Хадлум «краснеет», следовательно, ее беременность была совершенно точно экстремальна. Прокрутив данные до конца, вы увидите, что красных ячеек больше нет, но есть девять желтых. Это очень похоже на примерно одну точку из 100, что и предполагалось в нормальных данных согласно правилу.

Ограничения этого нехитрого метода

Границы Тьюки работают только при выполнении всех трех условий:

1. Данные, в общем, распределены нормально. Распределение может не быть идеальным, но кривая должна быть колоколообразной и обнадеживающе симметричной, без разных длинных хвостов, вылезающих с одной стороны.

2. Выброс «отмечен» как экстремальное значение на внешней стороне распределения.

3. Данные одномерны.

Рассмотрим пример выброса, который не удовлетворяет первым двум условиям.

В «Братстве Кольца», объединившись, наконец, в одну компанию (братство, в честь которого и названа книга), герои встают небольшой группой и слушают лидера эльфов, произносящего речь о том, кто они есть и какова их цель.

В этой группе есть четверо высоких ребят – Гэндальф, Арагорн, Леголас и Боромир – и четверо приземистых. Это хоббиты: Фродо, Мерри, Пиппин и Сэм.

Среди них есть один гном – Гимли. Гимли ниже первых на две головы, но выше вторых примерно настолько же (рис. 9–4).

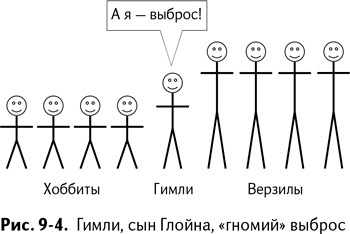
В фильме, когда мы впервые видим эту группу, Гимли явно выделяется по росту. Он не принадлежит ни к одной из групп.

Но является ли он выбросом? Его рост не ниже всех и не выше. На самом деле, его рост ближе всего к среднему в группе.

Понимаете, это распределение роста ничем не похоже на нормальное. Можете называть его «мультимодальным», если хотите (распределение с несколькими пиками). И Гимли является выбросом не из-за выдающегося роста, а всего лишь оттого, что находится между двумя пиками. А если данные многомерны, то такие точки в них найти еще сложнее.

Такой вид выбросов довольно часто обнаруживается в случаях мошенничества. Кто-то слишком обычный, чтобы быть обычным. Берни Мейдофф – отличный пример такого выброса. Если в большей части схем Понци предлагался размер выплат более 20 % сверху, больше похожий на выброс, то Мейдофф стал предлагать скромные надежные выплаты, смешивающиеся с шумом каждый год – он не перепрыгивал никаких границ Тьюки. Но постепенно эти выплаты из-за своей надежности превратились в многомерный выброс.

Так как же находить выбросы в случае многомодельности, многомерности данных (это все можно назвать простыми словами «данные из реального мира»)?

Один чудесный способ решения этого вопроса – отнестись к данным как к графу (см. поиск кластеров данных в главе 5). Задумайтесь над этим. Что определяет Гимли как выброс относительно остальных точек данных – это расстояние от него до них относительно расстояния между ними самими.

Все эти расстояния, от одной точки до другой, определяют ребра графа. С его помощью можно «выманить» изолированные точки. Для этого нужно начать с создания графа k ближайших соседей и плясать от него.

Назад: Выбросы тоже (плохие?) люди!

Дальше: Ни в чем не ужасен, плох во всем