Книга: Много цифр. Анализ больших данных при помощи Excel
Назад: Реальная жизнь: кластеризация методом k-средних в электронном маркетинге
Дальше: Подытожим
K-медианная кластеризация и асимметрическое измерение расстояний
Как правило, стандартной кластеризации по k-средним евклидовыми расстояниями бывает вполне достаточно, но тут мы столкнулись с небольшими проблемами, которые часто встречаются при кластеризации данных, имеющих большой разброс (розничная ли это торговля, классификация ли текстов или биоинформатика).
Использование k-медианной кластеризации
Первая очевидная проблема заключается в том, что ваши кластерные центры выражены десятыми долями от единицы, притом что вектор сделок каждого покупателя – точный ноль или единица. Что на самом деле значит 0,113 для сделки? Я хочу, чтобы кластерные центры выражали либо совершение сделки, либо ее отсутствие!
Если немного изменить алгоритм кластеризации, чтобы он использовал только величины векторов сделок покупателей, то он уже будет называться кластеризацией по k-медианам, а не по k-средним.
А если вы не хотите изменять евклидовым расстояниям, то все, что вам нужно – это добавить бинарное условие (bin) в «Поиске решения» для всех кластерных центров.
Но если кластерные центры теперь бинарны, то как использовать евклидово расстояние?
Переходим к соответствующему измерению расстояний
Переключившись с k-средних на k-медианы, люди обычно перестают пользоваться евклидовым расстоянием и начинают использовать нечто под названием манхэттенское расстояние, или метрика городского квартала.
Несмотря на то, что расстояние от точки А до точки В измеряется по прямой, такси на Манхэттене приходится перемещаться по сети прямых улиц, где возможны движения лишь на север, юг, запад или восток. Поэтому, если на рис. 2-13 вы видели, что расстояние между танцором-школьником и его кластерным центром равняется примерно 4,47, его манхэттенское расстояние будет равно 6 метрам (4 метра вниз + 2 метра вбок).
В терминах бинарных данных, таких как данные о продажах, манхэттенское расстояние между кластерным центром и покупательским вектором – это просто число несоответствий. Если у кластерного центра 0 и у меня 0, то в этом направлении расстояние будет 0, а если встречаются 0 и 1, то есть числа не совпадают, то в этом направлении расстояние равно 1. Складывая их, вы получаете общее расстояние, которое является просто числом несовпадений.
Действительно ли манхэттенское расстояние играет в решении ключевую роль?
Перед тем, как погрузиться с головой в k-медианную кластеризацию с использованием манхэттенского расстояния, остановитесь и подумайте о данных.
Что значит «покупатель совершил сделку»? Это значит, что он действительно хотел приобрести этот товар!
Что значит «покупатель не совершил сделку»? Значит ли это, что он не хотел этот товар настолько, насколько хотел тот, который купил? Одинаково ли сильны положительный и отрицательный сигналы? Может, он и любит шампанское, но уже держит запас в подвале. Может, он просто не видел вашу рассылку за этот месяц. Есть масса причин, почему кто-то чего-то не делает, но всего несколько – почему действия совершаются.
Другими словами, стоит обращать внимание на заказы, а не на их отсутствие.
Есть затейливое словцо – «асимметрия» данных. Единицы более ценны, чем нули. Если один покупатель совпадает с другим по трем единицам, то это более важное совпадение, чем с третьим покупателем по трем нулям. Что бросается в глаза – так это малое количество ценных единиц в данных – вот они, «разреженные данные»!
Но подумайте, что означает для покупателя близость к кластерному центру с евклидовой точки зрения. Если у одного покупателя 1 по одной сделке и 0 по другой, оба эти значения одинаково важны при расчете, насколько бы близко к кластерному центру покупатель ни располагался.
Вам нужен расчет асимметричного расстояния. А для переменных данных в бинарном коде вроде этих заказов вина существует уйма неплохих вариантов.
Самый, наверное, широко используемый метод подсчета асимметричного расстояния для данных формата 0–1 называется расстоянием по косинусу.
Расстояние по косинусу – это не так страшно, несмотря на тригонометрию
Самый простой способ объяснить, что такое расстояние по косинусу – это проанализировать понятие «близость по косинусу».
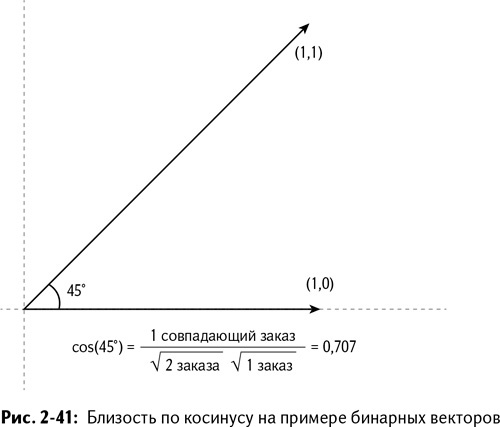
Рассмотрим пару двумерных бинарных векторов (1,1) и (1,0). В первом векторе были заказаны оба товара, в то время как во втором только первый. Вы можете представить эти векторы в пространстве и увидеть, что угол между ними – 45 градусов (рис. 2-41). Доставайте транспортир – проверим.
Можно сказать, что их близость равна косинусу 45 градусов, что составляет 0,707. Но почему?
Оказывается, косинус угла между двумя бинарными заказами – это:
Число совпадений заказов в двух векторах, разделенное на произведение квадратных корней количества заказов первого и второго векторов
В нашем случае два вектора (1,1) и (1,0) имеют один совпадающий заказ, так что в числителе будет 1, а в знаменателе – квадратный корень из 2 (две заключенные сделки), умноженный на корень из 1 заключенной сделки. В результате имеем 0,707 (рис. 2-41).
Что примечательного в этом расчете?
Причины три:
• счетчик в формуле считает только совпадения сделок, то есть он асимметричен и поэтому отлично подходит к данному случаю;
• квадратные корни из количества сделок по каждому вектору в знаменателе обращают наше внимание на тот факт, что вектор, в котором совершены все сделки – назовем его неразборчивым – гораздо дальше отстоит от другого вектора, чем тот, в котором совершены те же сделки и не совершены несколько других. Вам нужно совпадение векторов, «вкусы» которых совпадают, а не один вектор, содержащий «вкусы» другого.
• для бинарных данных эта близость находится в промежутке между 0 и 1, причем у двух векторов не получается 1, пока все их заказы не совпадут. Это означает, что 1 – близость по косинусу может использоваться как мера расстояния, называемая расстоянием по косинусу, которое также варьируется от 0 до 1.
А теперь все то же самое, но в Excel
Пришло время дать шанс проявить себя k-медианной кластеризации с помощью расстояния по косинусу.
Заметка
Кластеризация с помощью расстояния по косинусу также иногда называется сферической по k-средним. В главе 10 вы увидите сферические k-средние в R.
Будем последовательны и продолжим с k= 5.
Снова начнем с копирования листа 5МС и переименования его, на этот раз в 5MedC. Так как кластерные центры должны быть бинарными, нужно удалить все, что туда понаписал «Поиск решения».
Единственные вещи, требующие изменения здесь (кроме добавления бинарного условия в «Поиск решения» для k-медиан), – это расчеты расстояний в строках с 34 по 38. Начните с ячейки М34, в которой находится расстояние между Адамсом и центром кластера 1.
Чтобы сосчитать совпадения сделок у Адамса и кластера 1, нужно применить к этим двум столбцам SUMPRODUCT/СУММПРОИЗВ. Если у одного из них или у обоих встречается 0, строка остается пустой, но если у обоих 1, то это совпадение обрабатывается SUMPRODUCT/СУММПРОИЗВ и 1, помноженная на 1, остается 1.
Что касается извлечения корня из количества сделок, совершенных в векторе, это просто SQRT//КОРЕНЬ, наложенный на SUM//СУММА вектора. Таким образом, уравнение расстояния можно записать как
=1-SUMPRODUCT(M$2:M$33,$H$2:$H$33)/
(SQRT(SUM(M$2:M$33))*SQRT(SUM($H$2:$H$33)))
=1-СУММПРОИЗВ(M$2:M$33,$H$2:$H$33)/
(КОРЕНЬ(СУММА(M$2:M$33))*КОРЕНЬ(СУММА($H$2:$H$33)))
Обратите внимание на «1–» в начале формулы, что отличает близость по косинусу от расстояния по косинусу. Также, в отличие от евклидова расстояния, расчет расстояния по косинусу не требует использования формул массива.
Так или иначе, когда вы вставите это в М34, следует добавить проверку на ошибки на случай, если кластерный центр окажется 0:
=IFERROR(1-SUMPRODUCT(M$2:M$33,$H$2:$H$33)/
(SQRT(SUM(M$2:M$33))*SQRT(SUM($H$2:$H$33))),1)
=ЕСЛИОШИБКА(1-СУММПРОИЗВ(M$2:M$33,$H$2:$H$33)/
(КОРЕНЬ(СУММА(M$2:M$33))*КОРЕНЬ(СУММА($H$2:$H$33))),1)
Добавление формулы IFERROR/ЕСЛИОШИБКА избавляет вас от деления на 0. И если по какой-то причине «Поиск решения» выбирает кластерный центр, полностью состоящий из 0, вы можете предположить, что этот центр находится на расстоянии 1 от всего остального (1 как наибольшее значение бинарной переменной).
Затем вы можете скопировать М34 вниз по столбцу до М38 и изменить ссылки столбца H на I, J, K или L. Так же, как в случае с евклидовым расстоянием, вы используете абсолютные ссылки ($) в формуле, так что можете перетаскивать ее куда вздумается без ущерба для столбца с кластерным центром.
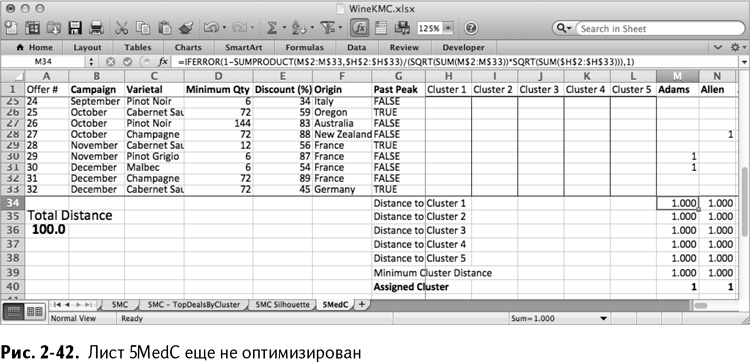
Таким образом, мы получили лист 5MedC (рис. 2-42), который пока абсолютно идентичен листу 5МС, с которым мы работали ранее.
Теперь, чтобы найти кластеры, откройте «Поиск решения» и измените условие «<= 1» для Н2:L33 на бинарное.
Нажмите «Выполнить». Вы можете отдохнуть полчасика, пока компьютер ищет для вас оптимальные кластеры. Вы сразу заметите, что все кластерные центры теперь – бинарные, так что у условного форматирования остаются два оттенка, что сильно повышает контраст.
Рейтинг сделок для 5-медианных кластеров
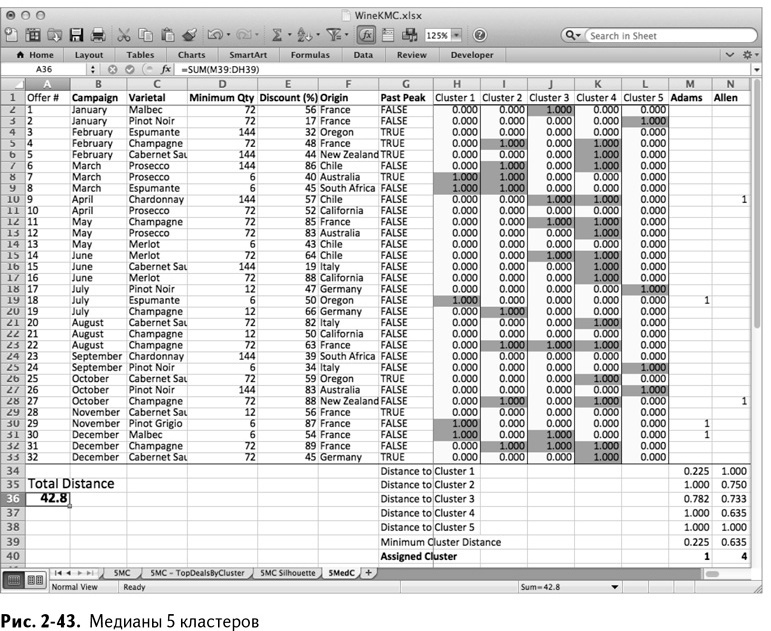
По завершении работы «Поиска решения» у вас образуется 5 кластерных центров, и в каждом – кучка единичек, указывающих на сделки, предпочитаемые этим кластером. Мой «Поиск решения» выдал оптимальное объективное значение 42,8, хотя ваше может серьезно отличаться (рис. 2-43).
Давайте разберемся в этих кластерах, используя метод подсчета сделок, которым мы пользовались для k-средних. Для этого сперва скопируйте лист 5MC – TopDealsByCluster tab и назовите его 5MedC – TopDealsByCluster.
Все, что нужно сделать на этом листе, чтобы заставить его работать, – это найти и заменить 5МС на 5MedC. Так как общий вид столбцов и строк у этих двух листов идентичен, все вычисления пройдут гладко, если ссылка на лист изменена.
Ваши кластеры могут немного отличаться от моих и по порядку, и по составу из-за эволюционного алгоритма, но, надеюсь, отличия будут несущественными. Давайте пройдемся по кластерам и посмотрим, как этот алгоритм разделил покупателей.
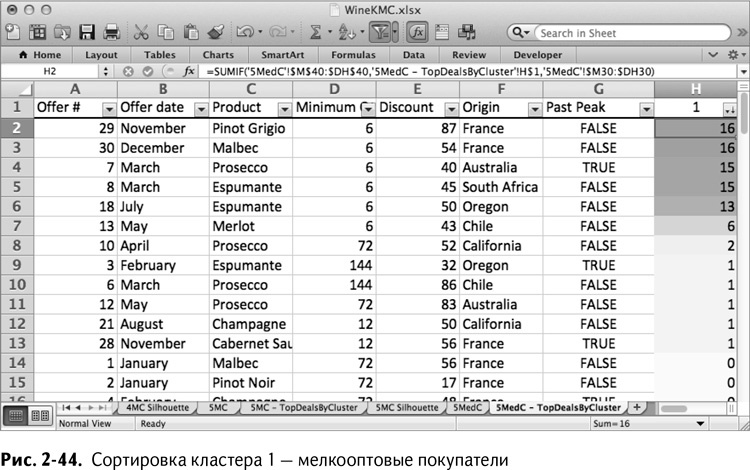
Сортировка кластера 1: похоже, это мелкооптовый кластер (рис. 2-44).
В кластер 2 попали покупатели, приобретающие только игристые вина. Шампанское, просекко и игристое доминируют в первых 11 позициях кластера (рис. 2-45). Интересно отметить, что подход k-средних не очень явно демонстрирует кластер любителей шипучего при k равном 4 или 5.
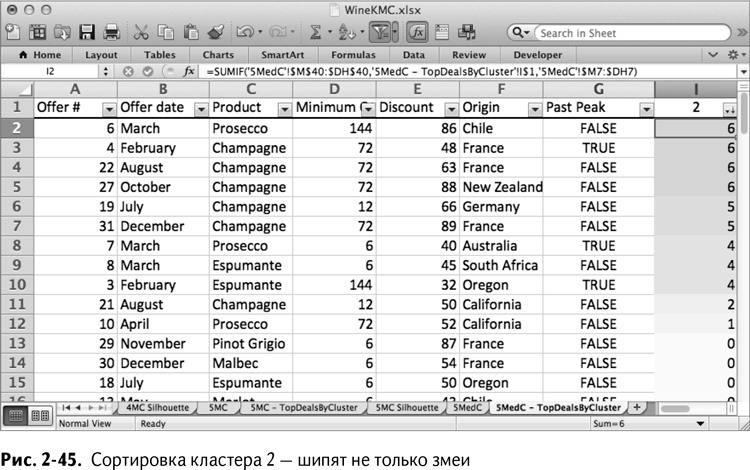
Кластер 3 – кластер франкофилов. Пять самых крупных сделок – на французские вина (рис. 2-46). Разве они не знают, что калифорнийские вина лучше?
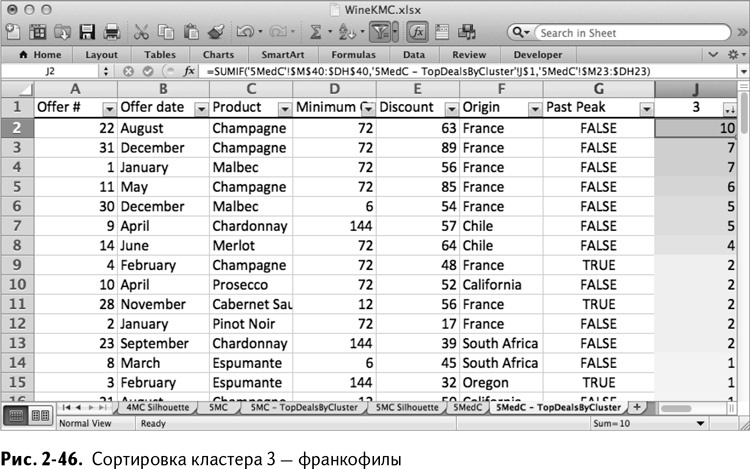
Что касается кластера 4, то здесь только крупные сделки. И все самые популярные сделки – с большой скидкой и еще не прошли ценовой максимум (рис. 2-47).
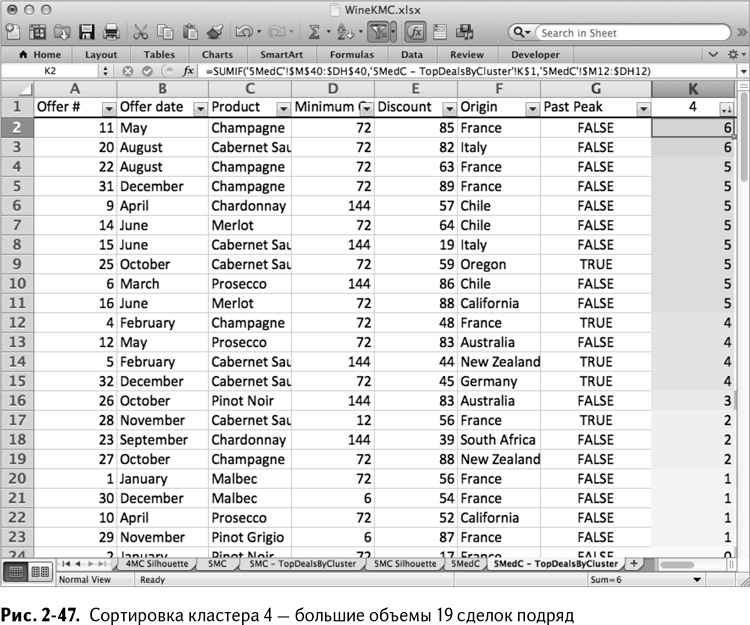
Кластер 5 снова оказался кластером пино нуар (рис. 2-48).
Так почище, не правда ли? Это оттого, что метод k-медиан, используя асиметричные методы измерения расстояний вроде равенства косинусов, позволяет кластеризировать клиентов, основываясь больше на их предпочтениях, чем на антипатиях. Ведь нас интересует именно это!
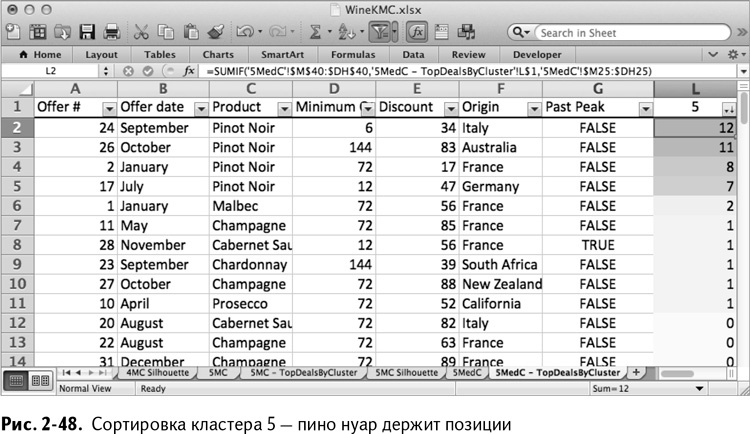
Вот на что способна мера расстояния!
Теперь вы можете взять привязки к этим пяти кластерам, импортировать их обратно в MailChimp.com как объединенное поле в списке писем и использовать эти значения для настройки вашей маркетинговой рассылки по кластерам. Это должно помочь вам лучше подбирать покупателей и управлять продажами.

