Книга: Много цифр. Анализ больших данных при помощи Excel
Назад: Девочки танцуют с девочками, парни чешут в затылке
Дальше: K-медианная кластеризация и асимметрическое измерение расстояний
Реальная жизнь: кластеризация методом k-средних в электронном маркетинге
Давайте перейдем к более предметному случаю. Я занимаюсь электронным маркетингом, поэтому приведу пример из жизни MailChimp.com, в которой работаю. Этот же самый пример будет работать и на данных о розничной торговле, преобразовании рекламного трафика, социальных сетей и т. д. Он взаимодействует практически с любым типом данных, связанных с донесением до клиентов рекламного материала, после чего они безоговорочно выбирают вас.
Оптовая Винная Империя Джоуи Бэг О'Донатса
Представьте на минуту, что вы живете в Нью-Джерси, где держите Оптовую Винную Империю Джоуи Бэг О'Донатса. Это импортно-экспортный бизнес, целью которого является доставка огромного количества вина из-за границы и продажи его определенным винным магазинам по всей стране. Этот бизнес работает таким образом, что Джоуи путешествует по всему миру в поисках невероятных сделок с большим количеством вина. Он отправляет его к себе в Джерси, а пристроить присланное в магазины и получить прибыль – ваша забота.
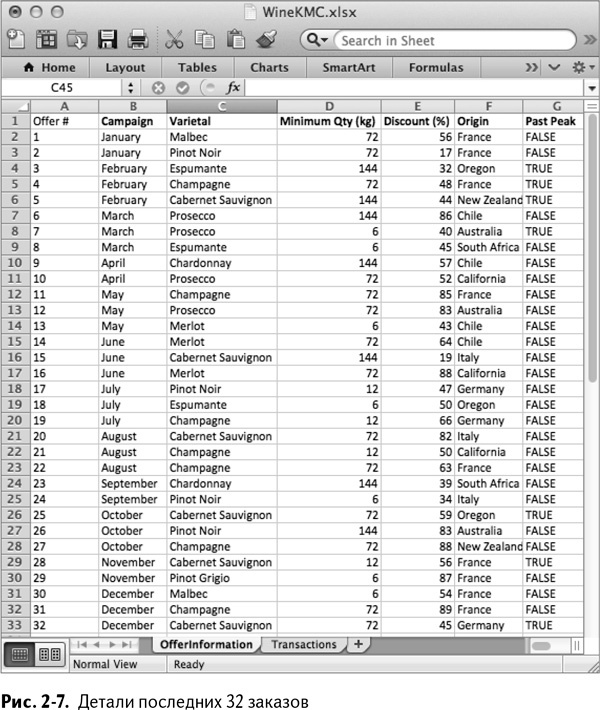
Вы находите покупателей разными способами: страница на Facebook, аккаунт в Twitter, порой даже прямая рассылка – ведь электронные письма «раскручивают» большинство видов бизнеса. В прошлом году вы отправляли одно письмо в месяц. Обычно в каждом письме описываются две или три сделки, скажем, одна с шампанским, а другая с мальбеком. Некоторые сделки просто удивительны – скидка составляет 80 % или больше. В итоге вы заключили около 32 сделок за год и все они прошли более-менее гладко.
Но то, что дела идут просто хорошо, не значит, что они не могут идти лучше. Было бы нелишне чуть глубже понять мотивы своих покупателей. Конечно, взглянув на конкретный заказ, вы видите, что некий Адамс купил сколько-то игристого в июле с 50 %-ной скидкой, но не можете определить, что подвигло его на покупку. Понравился ли ему минимальный объем заказа в одну коробку с шестью бутылками или цена, которая еще не поднялась до своего максимума?
Было бы неплохо иметь возможность разбить список клиентов на группы по интересам. Тогда вы бы могли отредактировать письма к каждой группе отдельно и, возможно, раскрутили бы бизнес еще больше. Любая подходящая данной группе сделка могла стать темой письма и идти в первом абзаце текста. Такой тип целевой рассылки может вызвать форменный взрыв продаж!
Но как разделить список рассылки? С чего начать?
Есть возможность дать компьютеру сделать работу за вас. Используя кластеризацию методом k-средних, вы можете найти наилучший вариант разбиения на группы, а затем попытаться понять, почему же он лучший.
Исходный набор данных
Заметка
Документ Excel, который мы будем разбирать в этой главе, находится на сайте книги – www.wiley.com/go/datasmart. В нем содержатся все исходные данные на случай, если вам захочется поработать с ними. Или же вы можете просто следить за текстом, подглядывая в остальные листы документа.
Для начала у вас есть два интересных источника данных:
• метаданные по каждому заказу сохранены в электронной таблице, включая сорт, минимальное количество вина в заказе, скидку на розничную продажу, информацию о том, пройден ли ценовой максимум, и о стране происхождения. Эти данные размещены во вкладке под названием OfferInformation, как показано на рис. 2–7;
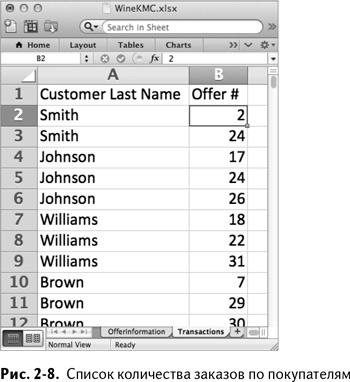
• зная, кто из клиентов что заказывает, вы можете вытряхнуть эту информацию из MailChimp и скормить электронной таблице с метаданными предложений во вкладке «Transactions». Это переменные данные, представленные, как показано на рис. 2–8, очень просто: покупатель и его заказ.
Определяем предмет измерений
И вот задача. В проблеме школьных танцев измерение расстояния между присутствующими и определение кластерных центров были несложными, не так ли? Достаточно просто найти подходящую рулетку!
Но что делать сейчас?
Вы знаете, что в прошлом году было 32 предложения сделок и у вас есть список из 324 заказов в отдельной вкладке, разбитый по покупателям. Но чтобы измерить расстояние от каждого покупателя до кластерного центра, вы должны поместить их в это 32-сделочное пространство. Иначе говоря, вам нужно понять, что за сделки они не совершили, и создать матрицу сделок по покупателям, в которой каждый клиент получает свой собственный столбец с 32 ячейками сделок, заполненные единицами, если сделки были совершены, и нулями, если нет.
Другими словами, вам нужно взять эту ориентированную по строкам таблицу сделок и превратить ее в матрицу, в которой клиенты располагаются по вертикали, а предложения – по горизонтали. Лучшим способом ее создать являются сводные таблицы.
Заметка
Чтобы узнать, что такое сводные таблицы, загляните в главу 1.
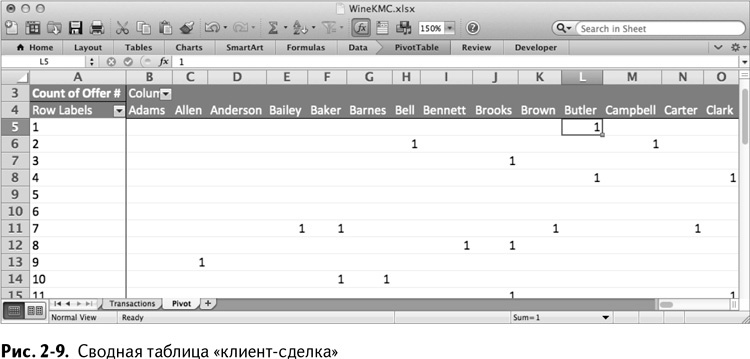
Алгоритм действия: на листе с переменными данными выделите столбцы А и В, а затем вставьте сводную таблицу. Используя Мастер создания сводных таблиц, просто выберите сделки как заголовок строки, а покупателей как заголовок столбца и заполните таблицу. В ячейке будет 1, если пара «клиент-сделка» существует, и 0, если нет (в данном случае 0 отображается как пустая ячейка). В результате получается таблица, показанная на рис. 2–9.
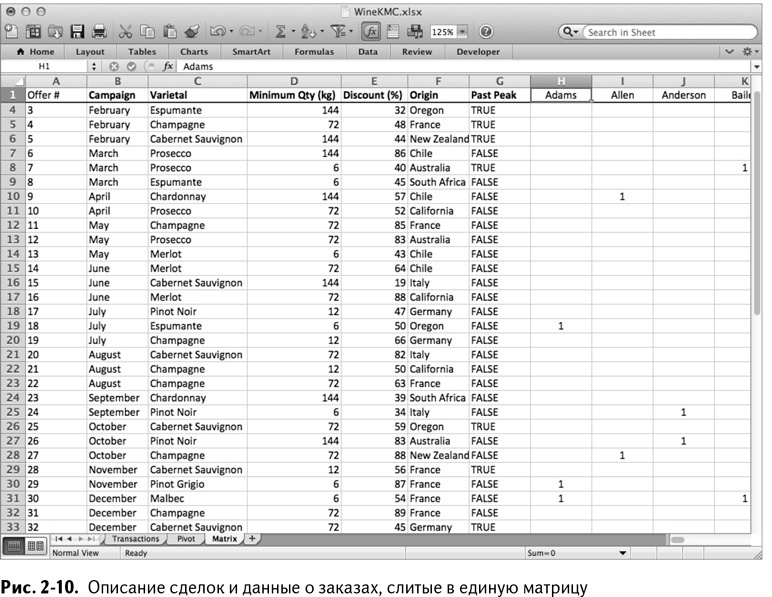
Теперь, когда у вас есть информация о заказах в формате матрицы, скопируйте лист OfferInformation и назовите его Matrix. В этот новый лист вставьте значения из сводной таблицы (не нужно копировать и вставлять номер сделки, потому что он уже содержится в информации о заказе), начиная со столбца Н. В итоге у вас должна получиться расширенная версия матрицы, дополненная информацией о заказах, как на рис. 2-10.
СТАНДАРТИЗАЦИЯ ДАННЫХ
В этой главе каждое измерение ваших данных представлено одинаково, в виде бинарной информации о заказах. Но во многих ситуациях, связанных с кластеризацией, мы не можем так сделать. Вообразите сценарий, в котором люди кластеризованы по росту, весу и зарплате. Все эти три вида данных имеют разную размерность. Рост может варьироваться от 1,5 до 2 метров, в то время как вес – от 50 до 150 кг.В этом контексте измерение расстояния между покупателями (как между танцорами в актовом зале) становится запутанным делом. Поэтому принято стандартизировать каждый столбец с данными, вычитая среднее и затем деля поочередно на меру разброса под названием среднеквадратичное отклонение, которое мы вычислим в главе 4. Таким образом, все столбцы приводятся к единой величине, количественно варьируясь около 0.Так как наши данные из главы 2 не требуют стандартизации, вы можете понаблюдать ее в действии в главе об определении выбросов – главе 9.
Начнем с четырех кластеров
Ну что ж, теперь все ваши данные сведены к единому удобному формату. Чтобы начать кластеризировать, нужно выбрать k – количество кластеров в алгоритме k-средних. Зачастую метод k-средних применяется так: берется набор различных k и проверяется по одному (как их выбирать, я объясню позже), но мы только начинаем – так что выберем лишь одно.
Вам понадобится количество кластеров, которое примерно подходит для того, чем вы хотите заняться. Вы явно не намерены создавать 50 кластеров и рассылать 50 целевых рекламных писем паре ребят из каждой группы. Это моментально лишает смысла наше упражнение. В нашем случае нужно что-то небольшое. Начните этот пример с 4 – в идеальном мире вы, возможно, разделили бы ваш список клиентов на 4 понятные группы по 25 человек в каждой (что в реальности маловероятно).
Итак, если придется разделить покупателей на 4 группы, как наилучшим образом их подобрать?
Вместо того чтобы портить симпатичный лист Matrix, скопируйте данные в новый лист и назовите его 4МС. Теперь вы можете вставить 4 столбца после ценового максимума в столбцы от Н до К, которые будут кластерными центрами. (Чтобы вставить столбец, кликните правой клавишей мышки на столбце Н и выберите «Вставить». Столбец появится слева.) Назовите эти кластеры от Cluster 1 до Cluster 4. Вы также можете применить на них условное форматирование, и когда бы вы ни установили их, вы сможете увидеть, насколько они отличаются.
Лист 4МС появится, как показано на рис. 2-11.
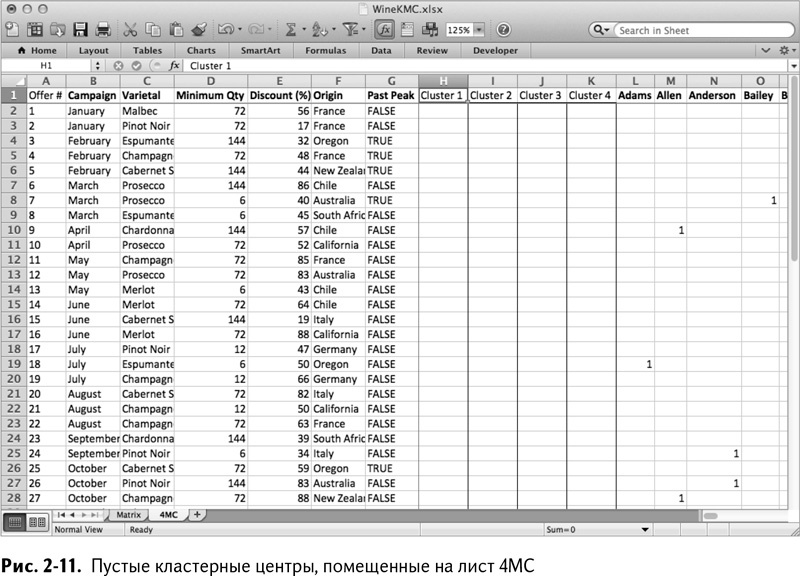
В данном случае все кластерные центры – нули. Но технически они могут быть какими угодно и, что вам особенно понравится – как на школьных танцах, распределены таким образом, что минимизируют расстояние между каждым покупателем и его кластерным центром.
Очевидно, что тогда эти центры будут иметь значения от 0 до 1 для каждой сделки, так как все клиентские векторы бинарны.
Но что означает «измерить расстояние между кластерным центром и покупателем»?
Евклидово расстояние: измерение расстояний напрямик
Для каждого клиента у вас есть отдельный столбец. Как же измерить расстояние между ними? В геометрии это называется «кратчайший путь», а расстояние, получаемое в результате, – евклидовым расстоянием.
Вернемся ненадолго в актовый зал и попробуем понять, как решить нашу проблему там.
Поместим координатные оси на полу и на рис. 2-12 увидим, что в точке (8,2) у нас танцор, а в (4,4) – кластерный центр. Чтобы рассчитать евклидово расстояние между ними, придется вспомнить теорему Пифагора, с которой вы знакомы еще со школьной скамьи.
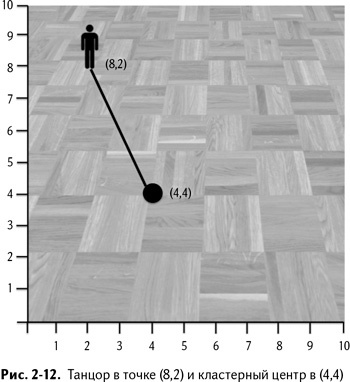

Эти две точки находятся в 8–4 = 4 метрах друг от друга по вертикали и в 4–2 = 2 метрах по горизонтали. По теореме Пифагора, квадрат расстояния между двумя точками равен 4^2+2^2 = 20 метрам. Отсюда мы вычисляем само расстояние, которое будет равно квадратному корню из 20, что составляет примерно 4,47 м (как на рис. 2-13).
В контексте подписчиков на рассылку у вас больше двух измерений, но применима та же концепция. Расстояние между покупателем и кластерным центром рассчитывается путем определения разниц между двумя точками для каждой сделки, возведения их в квадрат, сложения и извлечения квадратного корня.
К примеру, на листе 4МС вы хотите узнать евклидово расстояние между центром кластера 1 в столбце Н и заказами покупателя Адамса в столбце L.
В ячейке L34, под заказами Адамса, можно вычислить разницу между вектором Адамса и кластерным центром, возвести ее в квадрат, сложить и затем извлечь корень, используя следующую формулу для массивов (отметьте абсолютные ссылки, позволяющие вам перетаскивать эту формулу вправо или вниз без изменения ссылки на кластерный центр):
{=SQRT(SUM((L$2:L$33-$H$2:$H$33)^2))}
{=КОРЕНЬ(СУММА(L$2:L$33-$H$2:$H$33)^2))}
Формулу для массивов (введите формулу и нажмите Ctrl+Shift+Enter или Cmd+Return в MacOS, как сказано в главе 1) нужно использовать, потому что ее часть (L2:L33-H2:H33)^2 должна «знать», куда обращаться для вычисления разниц и возведения их в квадрат, шаг за шагом. Однако результат в итоге – единственное число, в нашем случае 1,732 (как на рис. 2-14). Он имеет следующий смысл: Адамс заключил три сделки, но так как изначальные кластерные центры – нули, ответ будет равняться квадратному корню из 3, а именно 1,732.
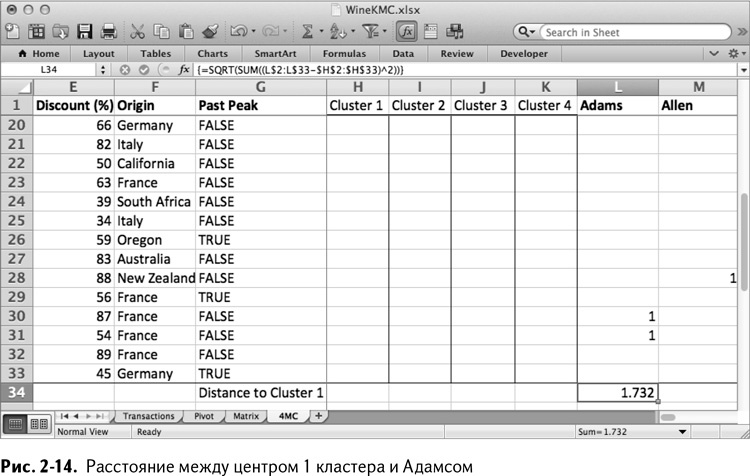
В электронной таблице на рис. 2-14 я закрепил верхнюю строку (см. главу 1) между столбцами G и Н и назвал строку 34 в ячейке G34 «Distance to Cluster 1», просто чтобы видеть, что где находится, если проматывать страницу вниз.
Расстояния и принадлежность к кластеру для всех!
Теперь вы знаете, как вычислить расстояние между вектором заказа и кластерным центром.
Пришло время добавить Адамсу расчет расстояний до остальных кластерных центров, перетянув ячейку L34 вниз на L37, а затем изменив вручную ссылку на кластерный центр со столбца Н на столбец I, J и К в ячейках ниже. В результате должны получиться следующие 4 формулы в L34:L37:
{=SQRT(SUM((L$2:L$33-$H$2:$H$33)^2))}
{=SQRT(SUM((L$2:L$33-$I$2:$I$33)^2))}
{=SQRT(SUM((L$2:L$33-$J$2:$J$33)^2))}
{=SQRT(SUM((L$2:L$33-$K$2:$K$33)^2))}
{=КОРЕНЬ(СУММА((L$2:L$33-$H$2:$H$33)^2))}
{=КОРЕНЬ(СУММА((L$2:L$33-$I$2:$I$33)^2))}
{=КОРЕНЬ(СУММА((L$2:L$33-$J$2:$J$33)^2))}
{=КОРЕНЬ(СУММА((L$2:L$33-$K$2:$K$33)^2))}
Так как вы использовали абсолютные ссылки для кластерных центров (ведь значок $ в формулах обозначает именно это, как было сказано в главе 1), можно перетащить L34:L37 в DG34:DG37, чтобы рассчитать расстояние от каждого покупателя до всех четырех кластерных центров. Озаглавьте строки в столбце G в ячейках с 35 по 37 «Distance to Cluster 2» и т. д. Свежерассчитанные расстояния показаны на рис. 2-15.
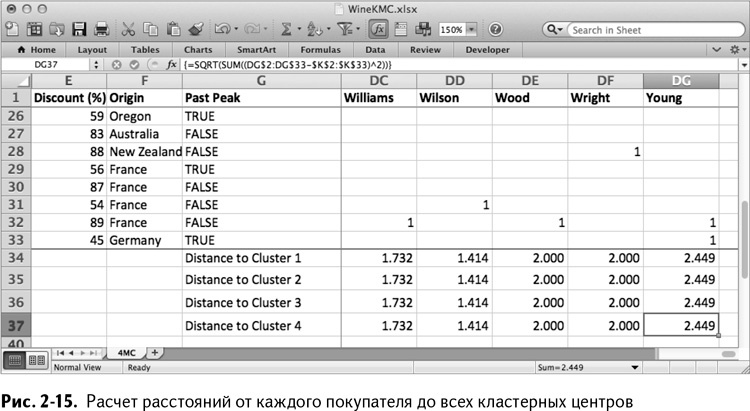
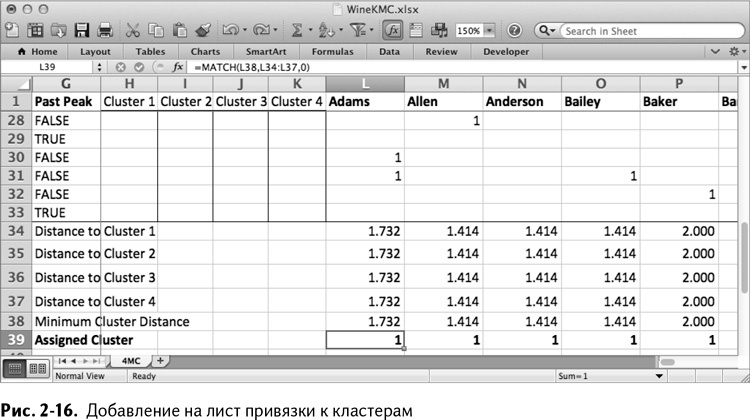
Теперь вам известно расстояние каждого клиента до всех четырех кластерных центров. Их распределение по кластерам произведено по кратчайшему расстоянию в два приема следующим образом.
Сначала вернемся к Адамсу в столбец L и рассчитаем минимальное расстояние до кластерного центра в ячейке L38. Это просто:
=MIN(L34:L37)
=МИН(L34:L37)
Для расчета используем формулу MATCH/ПОИСКПОЗ (подробнее в главе 1). Поместив ее в L39, вы можете увидеть номер ячейки из промежутка L34:L37 (считаю каждую по порядку от 1), которая находится на минимальном расстоянии:
=MATCH(L38,L34:L37,0)
=ПОИСКПОЗ(L38,L34:L37,0)
В данном случае расстояние одинаково для всех четырех кластеров, так что формула выбирает первый (L34) и возвращает 1 (рис. 2-16).
Вы можете также перетащить эти две формулы на DG38: DG39. Для пущей организованности добавьте названия строк 38 и 39 в ячейки 38 и 39 столбца G «Minimum Cluster Distance» и «Assigned Cluster».
Поиск решений для кластерных центров
Ваша электронная таблица пополнилась расчетом расстояний и привязкой к кластерам. Теперь, чтобы установить наилучшее положение кластерных центров, нужно найти такие значения в столбцах от Н до К, которые минимизируют общее расстояние между покупателями и кластерными центрами, к которым они привязаны, указанными в строке 39 для каждого покупателя.
Если вы внимательно читали главу 1, то должны знать, что делать, когда слышите слово «минимизировать»: начинается этап оптимизации, а оптимизация производится с помощью «Поиска решения».
Чтобы использовать «Поиск решения», вам понадобится ячейка для результатов, поэтому в А36 просуммируем все расстояния между покупателями и их кластерными центрами:
=SUM(L38:DG38)
=СУММА(L38:DG38)
Эта сумма расстояний от клиентов до ближайших к ним кластерных центров в точности является той целевой функцией, с которой мы встречались ранее, во время кластеризации актового зала средней школы Макакне. Но евклидово расстояние со своими степенями и квадратными корнями – чудовищно нелинейная функция, поэтому вам придется использовать эволюционный алгоритм решения вместо симплекс-метода.
В главе 1 вы уже пользовались этим методом. Симплексный алгоритм, если есть возможность его применить, работает быстрее других, но им нельзя воспользоваться для вычисления корней, квадратов и остальных нелинейных функций. Точно так же бесполезен OpenSolver, представленный в главе 1, который использует симплексный алгоритм, пусть даже и будто принявший стероиды.
В нашем случае встроенный в «Поиск решения» эволюционный алгоритм использует комбинацию случайного поиска и отличное решение «скрещивания», чтобы, подобно эволюции в биологическом контексте, находить эффективные решения.
Заметка
Оптимизация подробно описана в главе 4.
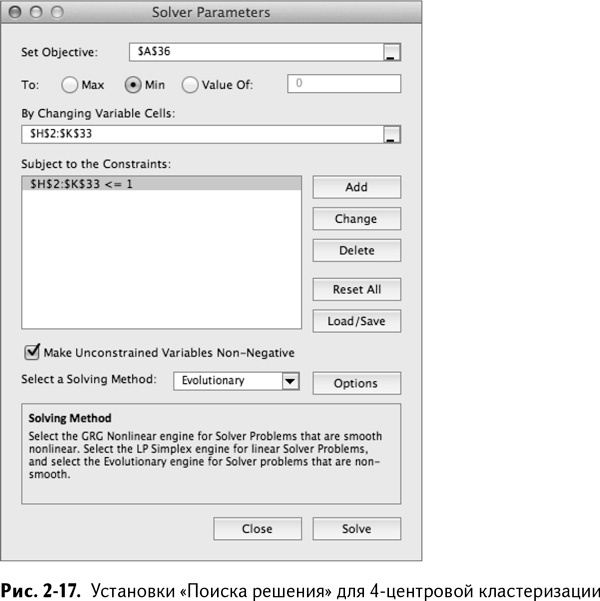
У вас есть все, что нужно для постановки задачи перед «Поиском решения»:
• цель: минимизировать общие расстояния от покупателей к их кластерным центрам (А36);
• переменные: вектор каждой сделки относительно кластерного центра (Н2:К33);
• условия: кластерные центры должны иметь значения в пределах от 0 до 1.
Рекомендуется наличие «Поиска решения» и молотка. Ставим задачу «Поиску решения»: минимизировать А36 путем изменения значений Н2:К33 с условием Н2:К33 <=1, как и все векторы сделок. Убедитесь, что переменные отмечены как положительные и выбран эволюционный алгоритм (рис. 2-17).
Но постановка задачи – еще не все. Придется немного попотеть, выбирая нужные опции эволюционного алгоритма, нажав кнопку «Параметры» в окне «Поиска решения» и перейдя в окно настройки. Советую установить максимальное время секунд на 30 побольше, в зависимости от того, сколько вы готовы ждать, пока «Поиск решений» справится со своей задачей. На рис. 2-18 я поставил свое на 600 секунд (10 минут). Таким образом, я могу запустить «Поиск решения» и пойти обедать. А если вам захочется прервать его пораньше, просто нажмите Escape и выйдите из него с наилучшим решением, которое тот успел найти.
Для тех, кому интересно: внутреннее устройство эволюционного алгоритма «Поиска решения» описано в главе 4 и на http://www.solver.com.

Нажмите «Выполнить» и наблюдайте, как Excel делает свое дело, пока эволюционный алгоритм не сойдется.
Смысл полученных результатов
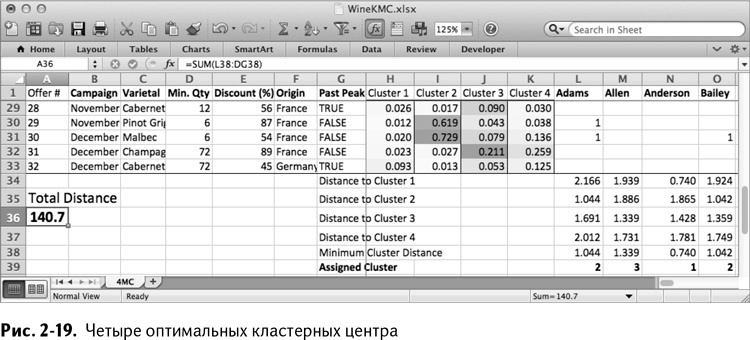
Как только «Поиск решения» выдает вам оптимальные кластерные центры, начинается самое веселое. Переходим к изучению групп! На рис. 2-19 мы видим, что «Поиск решения» нашел оптимальное общее расстояние 140,7, а все четыре кластерных центра – спасибо условному форматированию! – выглядят совершенно по-разному.
Имейте в виду, что ваши кластерные центры могут отличаться от представленных в книге, потому что эволюционный алгоритм использует случайные числа и ответ каждый раз получается разный. Кластеры могут быть совершенно другими или, что более вероятно, располагаться в другом порядке (к примеру, мой кластер 1 может быть очень близок к вашему кластеру 4 и т. д.).
Так как при создании листа вы вставили в столбцы от В до G описания сделок, теперь можно прочитать подробности на рис. 2-19, что важно для понимания идеи кластерных центров.
Для кластера 1 в столбце Н условное форматирование выбирает сделки 24, 26, 17 и, в меньшей степени, 2. Прочитав описание этих сделок, можно понять, что у них общего: они все заключались на пино нуар.
Взглянув на столбец I, вы увидите, что во всех зеленых ячейках низкое минимальное количество. Это покупатели, которые не желают приобретать огромные партии в процессе сделки.
А вот два остальных кластерных центра, честно говоря, сложно интерпретировать. Как насчет того, чтобы вместо интерпретации кластерных центров изучить самих покупателей в кластере и определить, какие сделки им нравятся? Это могло бы внести в вопрос ясность.
Рейтинг сделок кластерным методом
Вместо выяснения, какие расстояния до какого кластерного центра ближе к 1, давайте проверим, кто к какому кластеру привязан и какие сделки предпочитает.
Чтобы это сделать, начнем с копирования листа OfferInformation. Копию назовем 4МС – TopDealsByCluster. Пронумеруйте столбцы от Н до К на этом новом листе от 1 до 4 (как на рис. 2-20).
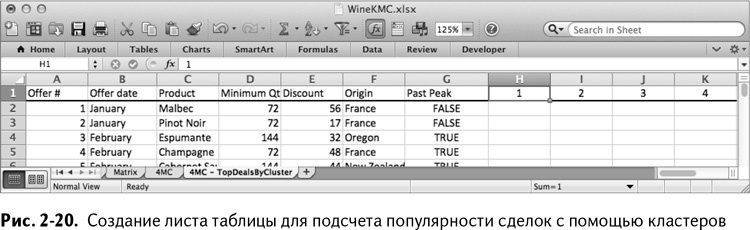
На листе 4МС у вас были привязки по кластерам от 1 до 4 в строке 39. Все, что вам нужно сделать, чтобы сосчитать сделки по кластерам, – это взглянуть на названия столбцов от Н до К на листе 4МС – TopDealsByCluster, посмотреть, кто из листа 4МС был привязан к этому кластеру в строке 39, а затем сложить количество их сделок в каждой строке. Таким образом мы получим общее количество покупателей в данном кластере, совершивших сделки.
Начнем с ячейки Н2, в которой записано количество покупателей кластера 1, принявших предложение № 1, а именно январский мальбек. Нужно сложить значения ячеек диапазона L2: DG2 на листе 4МС, но только покупателей из 1 кластера, что является классическим примером использования формулы SUMIF /СУММЕСЛИ. Выглядит она так:
=SUMIF('4MC'!$L$39:$DG$39,'4MC – TopDealsByCluster'! H$1,'4MC'!$L2:$DG2)
=СУММЕСЛИ('4MC'!$L$39:$DG$39,'4MC – TopDealsByCluster'! H$1,'4MC'!$L2:$DG2)
Эта формула работает таким образом: вы снабжаете ее некими условными значениями, которые она проверяет в первой части '4MC'!$L$39:$DG$39, затем сравнивает с 1 в заголовке столбца ('4MC – TopDealsByCluster'! H$1), а потом при каждом совпадении, прибавляет это значение в строку 2 в третьей части формулы '4MC'!$L2:$DG2.
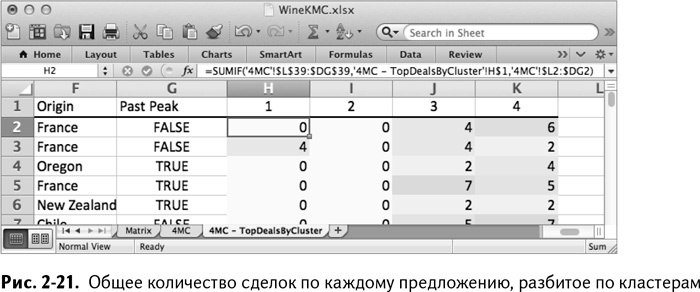
Заметьте, что вы использовали абсолютные ссылки ($ в формуле) перед всем, что относится к привязке к кластеру, номеру строки в заголовках столбцов и букве, обозначающей столбец, для совершенных сделок. Сделав эти ссылки абсолютными, можно перетащить формулу в любое место из Н2:К33, чтобы рассчитать количество сделок для других кластерных центров и комбинации сделок, как на рис. 2-21. Чтобы эти столбцы были более читаемы, вы также можете применить к ним условное форматирование.
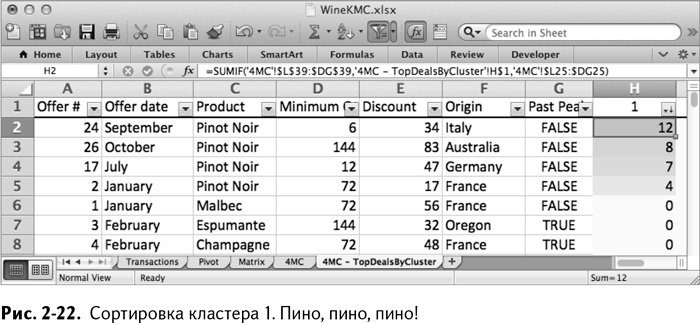
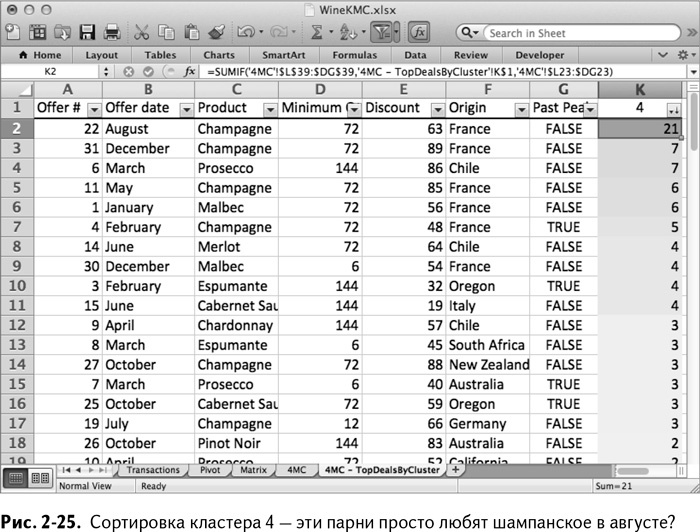
Выделяя столбцы от А до К и применяя автофильтрацию (глава 1), вы можете сортировать эти данные. Отсортировав от наименьшего к наибольшему столбец Н, вы увидите, какие сделки наиболее популярны в кластере 1 (рис. 2-22).
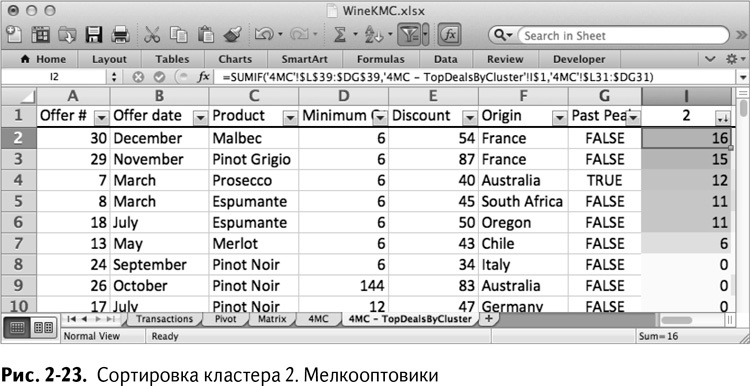
Как я упоминал ранее, четыре самых крупных сделки для этого кластера – это пино. Эти ребята явно злоупотребляют фильмом «На обочине». Если вы отсортируете кластер 2, то вам станет совершенно ясно, что это – мелкооптовые покупатели (рис. 2-23).
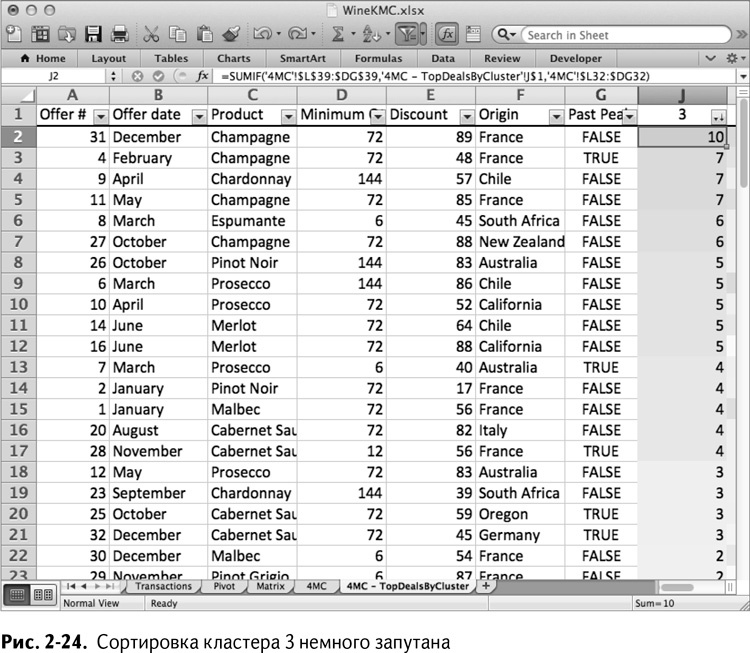
Но когда вы отсортируете кластер 3, понять что-либо будет не так просто. Крупные сделки можно пересчитать по пальцам, а разница между ними и остальными не так очевидна. Однако у самых популярных сделок все же есть что-то общее – довольно хорошие скидки, 5 из 6 самых крупных сделок – на игристое вино, и Франция – производитель товара для 3 из 4 из них. Тем не менее эти предположения неоднозначны (рис. 2-24).
Что касается кластера 4, то этим ребятам по какой-то причине явно понравилось августовское предложение на шампанское. Также 5 из 6 крупнейших сделок – на французское вино, а 9 из 10 первых по величине – на большой объем товара (рис. 2-25). Может, это тяготеющий к французским винам крупнооптовый кластер? Пересечение кластеров 3 и 4 тоже беспокоит.
И это подводит нас к вопросу: настолько ли хорошо подходит 4 для значения k в кластеризации по k-средним? Возможно, нет. Но как узнать?
Силуэт: хороший способ позволить разным значениям k посостязаться
Нет ничего плохого в том, чтобы кластеризировать методом k-средних несколько раз, перебирая различные k, пока не найдется такой результат, который будет иметь для вас интуитивный смысл. Конечно, возможно, причина отсутствия «хорошо читаемых результатов» заключается не только в том, что k подобрано неверно. Может быть, в информации о предложениях не хватает чего-то такого, что могло бы помочь понять кластеры лучше.
Так есть ли другой способ (кроме простого разглядывания кластеров) дать красный или зеленый свет конкретному значению k?
Он есть – и это вычисление для наших кластеров такого показателя, как силуэт. Прелесть его в том, что он относительно независим от значения k, так что можно сравнивать различные значения k, пользуясь одними и теми же параметрами.
Силуэт высокого уровня: насколько далеки от вас ваши соседи?
Вы можете сравнить среднее расстояние между каждым покупателем и его друзьями из его же кластера и покупателями из соседних кластеров (с ближайшими кластерными центрами).
Если я немного ближе к членам своего кластера, чем соседнего, то эти ребята – хорошая компания для меня, не так ли? Но что, если ребята из соседнего кластера практически так же близки ко мне, как и мои кластерные собратья? Выходит тогда, что моя привязка к кластерам немного сомнительна?
Вот как формально записать это значение:
(Среднее расстояние до членов ближайшего соседнего кластера – Среднее расстояние до членов своего кластера)/Максимум из этих двух средних
Знаменатель в расчете дает разброс итогового значения от –1 до 1.
Подумайте над этой формулой. Чем дальше от вас находящиеся в соседнем кластере (и тем менее они вам подходят), тем ближе к 1 значение этого показателя. А если два средних расстояния почти одинаковы? Тогда величина стремится к 0.
Расчет среднего по этой формуле для каждого покупателя дает нам силуэт. Если силуэт равен 1, это прекрасно. Если это 0, то, скорее всего, кластеры выбраны неверно. Если он меньше нуля, то многие покупатели с гораздо большим удовольствием проводили бы время в другом кластере, который совершенно ужасен.
Вы можете сравнить силуэты для различных значений k, чтобы увидеть, какое из них лучше.
Чтобы сделать эту концепцию более наглядной, вернемся к примеру со школьными танцами. Рис. 2-26 иллюстрирует расчет расстояний в формировании силуэта. Заметьте, что расстояние от одного из сопровождающих до двух других сравнивается с расстояниями до соседнего кластера – компании мальчишек.
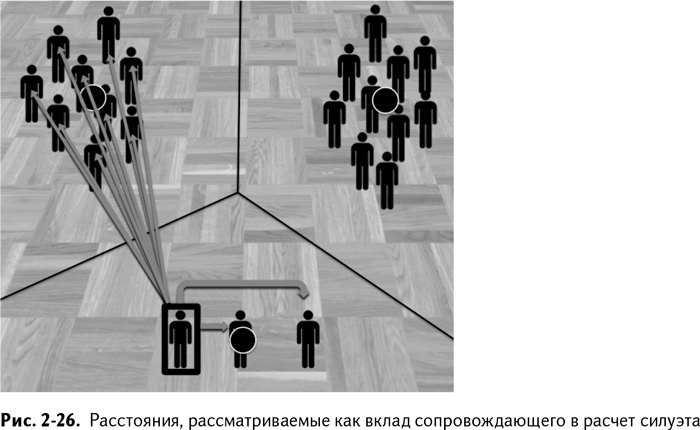
Видно, что двое других сопровождающих безусловно ближе, чем кучка неуклюжих тинейджеров, что делает результат расчета для этого сопровождающего гораздо больше нуля.
Создание матрицы расстояний
Для того чтобы применить силуэт, вам понадобится еще одна немаловажная часть данных, а именно расстояние между покупателями. И если кластерные центры могут перемещаться, то расстояние между двумя клиентами никогда не меняется. Так что можно просто создать отдельный лист Distances и использовать его во всех своих расчетах силуэтов, вне зависимости от того, какое k вы используете и где в конечном итоге окажутся ваши кластерные центры.
Начнем с создания чистого листа под названием Distances и вставки туда покупателей: по горизонтали – в первую строку и по вертикали – в первый столбец. Ячейка матрицы будет содержать расстояние между покупателем из строки и покупателем из столбца. Чтобы вставить клиентов в строку, скопируйте H1:DC1 из листа Matrix и, используя «Специальную вставку», вставьте значения, убедившись, что выбрали опцию «Транспонировать» в меню специальной вставки.
Вам нужно понимать, где в матрице какой покупатель, поэтому пронумеруйте их от 0 до 99 в обоих направлениях. Расположим эту нумерацию в столбце А и строке 1, для чего вставим пустые столбец и строку слева и сверху, соответственно, кликнув для этого правой клавишей мышки на строке и столбце и выбрав «Вставить».
Заметка
Между прочим, есть много способов поместить эту нумерацию 0–99 в Excel. К примеру, можно просто начать печатать 0, 1, 2, 3, а затем выделить их и потянуть за нижний угол выделенной области до конца списка клиентов. Excel поймет это и продолжит числовой ряд. В результате должна получиться пустая матрица, как на рис. 2-27.
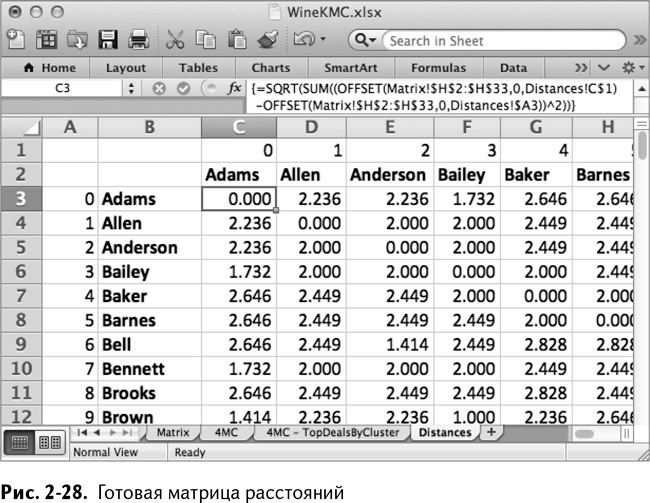
Рассмотрим ячейку С3, которая отображает расстояние между Адамсом и Адамсом, то есть между Адамсом и им же самим. Оно должно равняться нулю, верно? Ведь никто не может быть ближе к вам, чем вы сами!
Как же вы это рассчитали? А вот как: столбец Н на листе Matrix показывает вектор сделок Адамса. Чтобы вычислить евклидово расстояние между Адамсом и им самим, нужно просто вычесть столбец Н из столбца Н, возвести разницу в квадрат и извлечь из результата квадратный корень.
Но как применить этот расчет к каждой ячейке матрицы? Я бы ни за что не согласился печатать это вручную. Это бы заняло вечность. Что вам нужно – это формула OFFSET/СМЕЩ в ячейке С3 (эта формула подробно объясняется в главе 1).
Формула OFFSET/СМЕЩ берет фиксированный набор ячеек (в нашем случае это будет вектор сделок Адамса, Matrix!$H$2:$H$33) и перемещает его целиком на указанное количество строк и столбцов в нужном вам направлении.
Вот, например, OFFSET(Matrix!$H$2:$H$33,0,0) / СМЕЩ(Matrix!$H$2: $H$33,0,0) – это просто тот же вектор сделок Адамса, потому что вы передвинули исходный набор на 0 строк вниз и 0 столбцов вправо.
Но OFFSET(Matrix!$H$2:$H$33,0,1) / СМЕЩ(Matrix!$H$2:$H$33,0,1) – это столбец сделок Аллена.
OFFSET(Matrix!$H$2:$H$33,0,2) / СМЕЩ(Matrix!$H$2:$H$33,0,2) – столбец Андерсона, и т. д.
И здесь нам как раз и пригодится нумерация строк и столбцов 0–99. Вот, например:
{=SQRT(SUM((OFFSET(Matrix!$H$2:$H$33,0,Distances!C$1)-OFFSET(Matrix!$H$2:$H$33,0,Distances!$A3))^2))}
{=КОРЕНЬ(СУММА((СМЕЩ(Matrix!$H$2:$H$33,0,Distances!C$1) – СМЕЩ(Matrix!$H$2:$H$33,0,Distances!$A3))^2))}
Это расстояние между Адамсом и им самим. Обратите внимание: вы применяете Distances!C$1 для смещения столбца в векторе первой сделки и Distances!$А3 в векторе второй сделки.
Таким образом, когда вы перетаскиваете эту формулу по таблице, все остается привязанным к вектору сделок Адамса, но формула OFFSET/СМЕЩ смещает вектор на нужное количество строк и столбцов, используя нумерацию в строке 1 и столбце А. Точно так же она сравнивает два любых вектора сделок интересующих вас покупателей. На рис. 2-28 показана заполненная матрица расстояний.
Также не забывайте, что, как и на листе 4МС, эти расстояния – это формулы массивов.
Применение силуэтов в Excel
Ну что ж, теперь, когда у нас есть таблица расстояний, можно создать новый лист под названием 4МС Silhouette для окончательного расчета силуэта.
Начнем с копирования покупателей и их групповых привязок с листа 4МС и специальной вставки имен клиентов в столбец А, а привязок – в столбец В (не забудьте проверить, отмечено ли «Транспонирование» в меню специальной вставки).
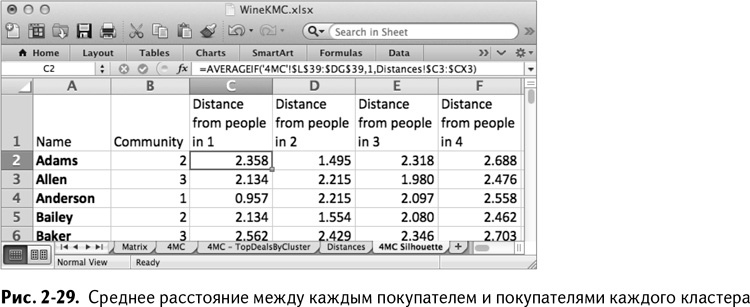
Теперь можно использовать лист Distances для расчета среднего расстояния между каждыми двумя покупателями из разных кластеров. Озаглавьте столбцы от С до F «Distance from People in 1» и далее до «Distance from People in 4».
В моем примере Адамс отнесен к кластеру 2, так что рассчитаем в ячейке С2 расстояние между ним и всеми клиентами кластера 1. Вам нужно просмотреть список покупателей, найти тех, кто относится к кластеру 1, и занести их средние расстояния до Адамса в строку 3 листа Distances.
Похоже на подходящий случай для формулы AVERAGEIF/СРЗНАЧЕСЛИ:
=AVERAGEIF('4MC'!$L$39:$DG$39,1,Distances!$C3:$CX3)
=СРЗНАЧЕСЛИ('4MC'!$L$39:$DG$39,1,Distances!$C3:$CX3)
AVERAGEIF/СРЗНАЧЕСЛИ проверяет привязки к кластеру и сравнивает их с кластером 1 перед усреднением соответствующих расстояний из С3:СХ3.
Для столбцов от D до F формулы одинаковые, за исключением того, что кластер 1 заменяется 2, 3, и 4. Теперь можно кликнуть на этих формулах дважды и скопировать их на всех покупателей, чтобы получить в результате таблицу, показанную на рис. 2-29.
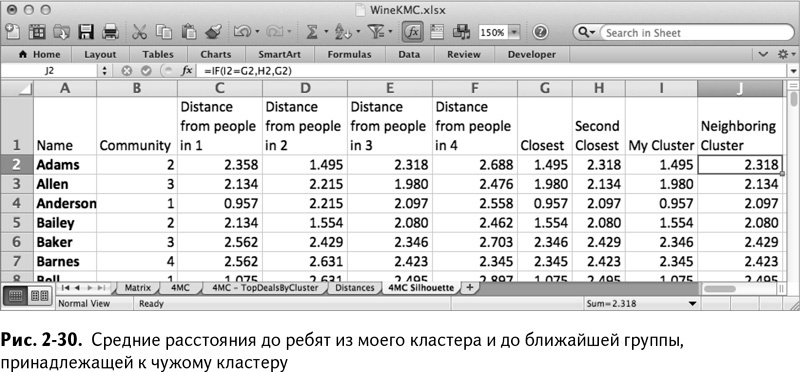
В столбце G можно рассчитать ближайшую группу покупателей, используя формулу MIN/МИН. Например, для Адамса это просто:
=MIN(C2:F2)
=МИН(С2:F2)
А в столбце Н можно вычислить вторую по близости группу покупателей, используя формулу SMALL/НАИМЕНЬШИЙ (цифра 2 в формуле указывает на второй результат):
=SMALL(C2:F2,2)
=НАИМЕНЬШИЙ(C2:F2,2)
Точно так же можно рассчитать расстояние до членов вашей собственной группы (которое, очевидно, такое же, как в столбце G, но не всегда) в столбце I:
=INDEX(C2:F2,B2)
=ИНДЕКС(C2:F2,B2)
Формула INDEX/ИНДЕКС пересчитывает столбцы с расстояниями до нужного вам от С до F, используя значение привязки из столбца В как индекс.
Для окончательного расчета силуэта вам понадобится расстояние до ближайшей группы покупателей, находящихся не в вашем кластере, которая, скорее всего, расположена в столбце Н, но не всегда. Чтобы получить эту величину в столбце J, нужно сравнить свое собственное кластерное расстояние в I с ближайшим кластером в G, и если они совпадут, то ответ – Н. В противном случае это G.
=IF(I2=G2,H2,G2)
=ЕСЛИ(I2=G2,H2,G2)
Скопировав все эти значения в столбец, вы получите электронную таблицу, показанную на рис. 2-30.
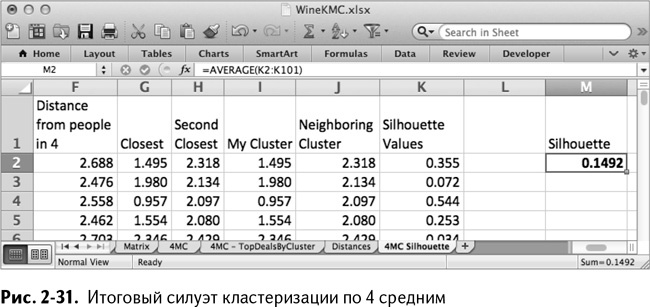
И, когда вы свели эти значения вместе, добавление значений силуэта для определенного покупателя в столбец К – пара пустяков:
=(J2-I2)/MAX(J2,I2)
=(J2-I2)/МАКС(J2,I2)
Вы можете просто скопировать эту формулу вниз по столбцу, чтобы получить величину для каждого покупателя.
Легко заметить, что для некоторых клиентов эта величина близка к 1. Например, значение силуэта для Андерсона в моем кластерном решении – 0,544 (рис. 2-31). Неплохо! Но для других покупателей, таких как Коллинз, значение меньше нуля. Если так пойдет и дальше, то Коллинзу будет лучше в соседнем кластере, чем в том, в котором он находится. Бедняга!
Теперь можно усреднить эти значения, чтобы получить итоговую фигуру силуэта. В моем случае, показанном на рис. 2-31, это 0,1492, что гораздо ближе к 0, чем к 1. Это удручает, но не особенно удивляет. В конце концов, два из четырех кластеров оказались не очень-то устойчивыми, когда мы попытались их интерпретировать с помощью описаний сделок.
Хорошо. Что же теперь?
Силуэт, безусловно, равен 0,1492. Но что это означает? Что с ним делать? Пробовать другие значения k! А затем снова обратиться к силуэту, чтобы узнать, насколько они лучше.
Как насчет пяти кластеров?
Попробуем поднять k до 5 и посмотреть, что будет.
Есть хорошая новость: так как вы уже делали расчет для 4 кластеров, вам не придется начинать все с чистого листа. Не нужно ничего делать с листом Distances. Он вполне сгодится и так.
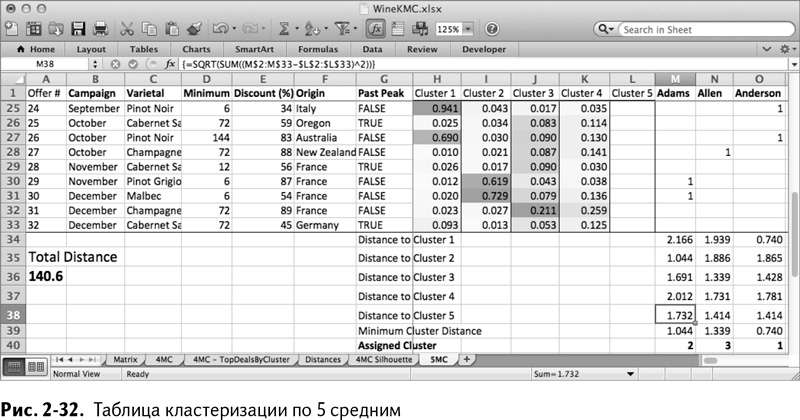
Создаем копию листа 4МС и называем ее 5МС. Все, что нужно – это добавить пятый кластер на лист и ввести его в свои расчеты.
Кликните для начала правой клавишей мыши на столбце L и вставим новый столбец, который назовем Cluster 5. Вам также нужно вставить расстояние в строку кластера 5, кликнув на строке 38 правой клавишей и выбрав «Вставить». Скопируйте расстояние в строку кластера 4 в 38 строке и поменяйте столбец с K на L, чтобы создать строку с расстоянием до кластера 5. Что касается строк Minimum Cluster Distance и Assigned Cluster, то ссылки на строку 37 нужно исправить на 38, чтобы включить в расчет новое кластерное расстояние.
В результате должна получиться таблица как на рис. 2-32.
Поиск решения для пяти кластеров
Открыв «Поиск решения», вам нужно только поменять $H$2:$K$33 на $H$2:$L$33 в переменных решения и разделах условий, чтобы включить новый кластер 5. Все остальное остается без изменений.
Нажмите «Выполнить» и запустите решение этой новой задачи.
Мой «Поиск решения» остановился на итоговом расстоянии 135,1, как показано на рис. 2-33.
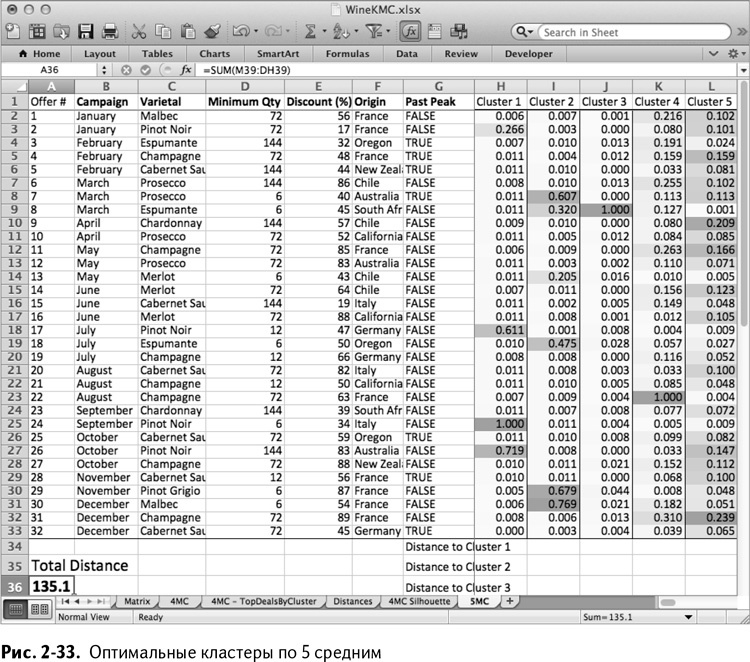
Рейтинг сделок для всех пяти кластеров
Отлично. Давайте посмотрим, как это делается.
Создайте копию листа 4MC – TopDealsByCluster tab и переименуйте его в 5MC – TopDealsByCluster. Придется еще подкорректировать несколько формул, чтобы все заработало.
Сначала убедитесь, что эта таблица упорядочена по номеру предложений в столбце 1. Затем назовите столбец L «5» и перетащите формулы из K в L. Выделите столбцы от А до L и примените автофильтрацию заново, чтобы сделать заказы кластера 5 сортируемыми.
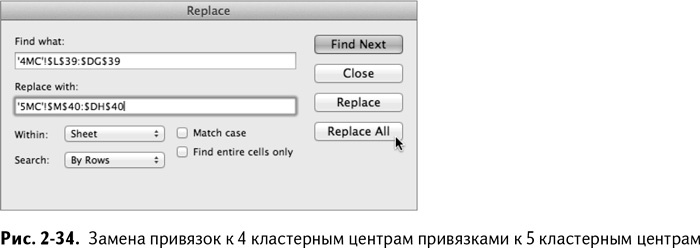
Все ссылки на этом листе ведут к листу 4МС, так что пришло время решительно все найти и заменить. Привязки к кластерам на листе 5МС смещены на одну строку вниз и один столбец вправо, поэтому ссылка на '4MC'!$L$39:$DG$39 в формуле SUMIF//СУММАЕСЛИ превратится в '5MC'!$M$40:$DH$40. Как показано на рис. 2-34, вы можете воспользоваться функцией «Найти и заменить».
Заметка
Не забывайте, что ваши результаты отличаются от моих из-за использования эволюционного алгоритма.
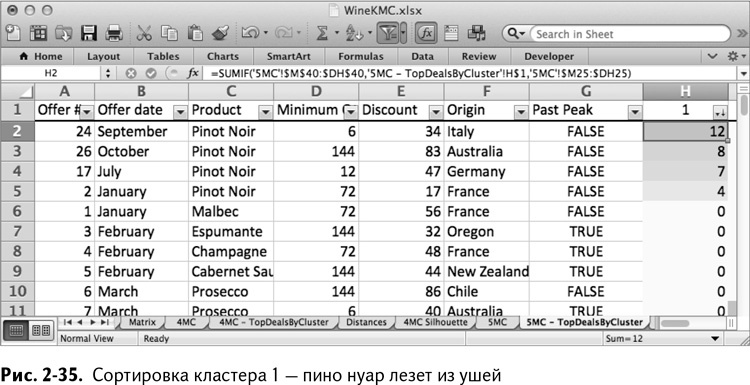
Сортируя кластер 1, мы снова ясно видим наш кластер пино нуар. (рис. 2-35).
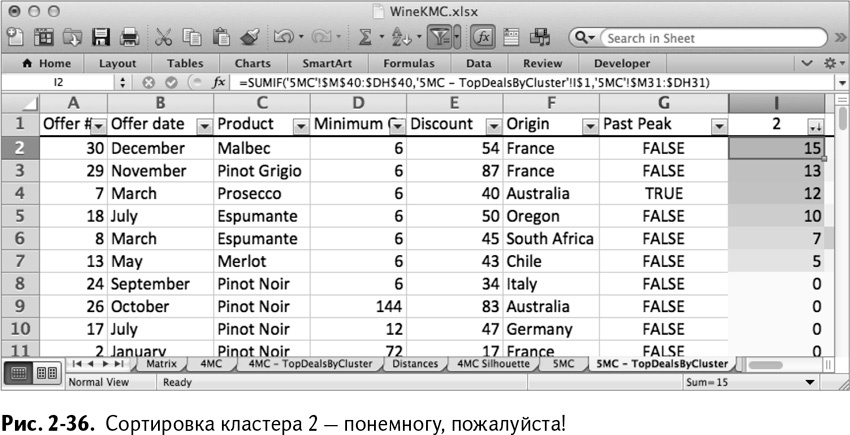
Кластер 2 – это кластер покупателей малых объемов (рис. 2-36).
Что касается кластера 3, то он снова взрывает мой мозг. Единственное, что можно в нем выделить – это, по какой-то причине, южноафриканское эспуманте (рис. 2-37).
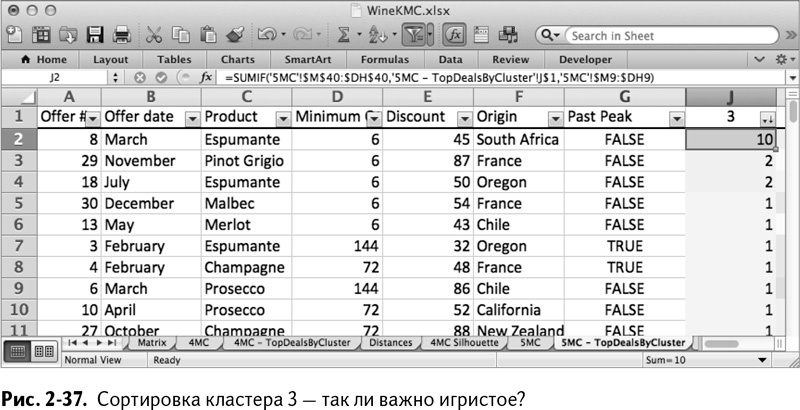
Покупатели кластера 4 заинтересованы в больших объемах, преимущественно французского вина и с хорошей скидкой. Здесь даже можно обнаружить склонность к игристым винам. Этот кластер сложно читается, в нем много что происходит (рис. 2-38).
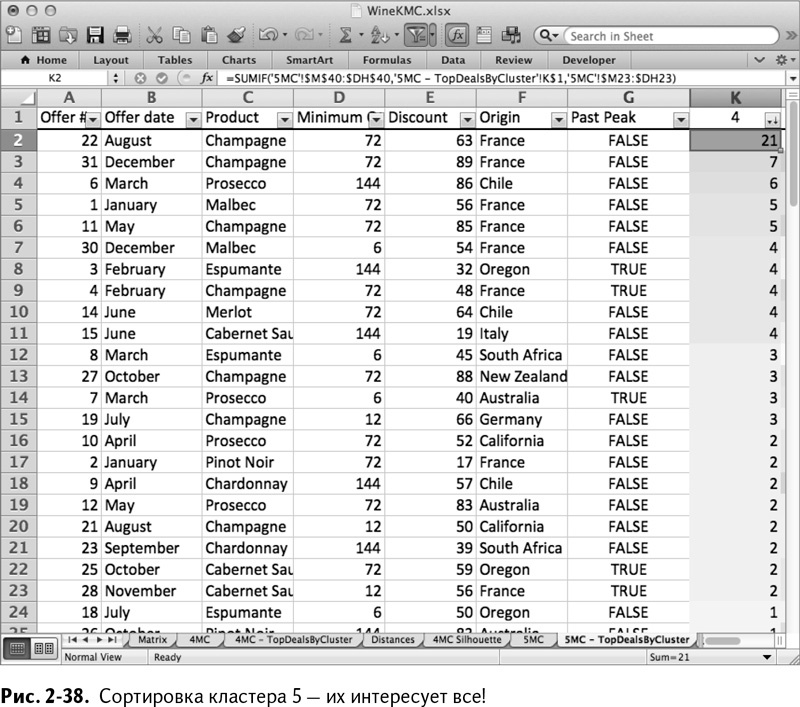
Сортировка кластера 5 даст результат, идентичный кластеру 4, хотя большие объемы и большие скидки похожи на основные тенденции (рис. 2-39).
Вычисление силуэта кластеризации по пяти средним
Вам, должно быть, интересно, чем пять кластеров лучше четырех. Результат-то, похоже, не сильно отличается. Давайте вычислим силуэт для пяти кластеров и посмотрим, что об этом думает компьютер.
Начнем с копирования листа 4МС Silhouette и переименования его в 5МС Silhouette. Теперь кликните правой клавишей мышки на столбце G, вставьте новый столбец и назовите его Distance From People in 5. Перетащите формулу из F2 в G2, поменяйте количество кластеров в переборе с 4 на 5, а затем кликните дважды на ячейке, чтобы заполнить весь столбец.
Точно так же, как и в предыдущей части, вам нужно найти и заменить '4MC'!$L$39:$DG$39 на '5MC'!$M$40:$DH$40.

В ячейки Н2, I2 и J2 нужно добавить расстояние до ребят из кластера 5, поэтому все диапазоны, заканчивающиеся на F2, должны быть расширены до G2. Затем выделите Н2:J2 и двойным щелчком в правом нижнем углу отправьте эти обновленные формулы вниз по столбцам.
И, наконец, скопируйте и вставьте с помощью «Специальной вставки» значения привязки к кластерам из строки 40 листа 5МС в столбец В листа 5МС Silhouette. Это также означает, что вы должны отметить «Транспонировать» в меню специальной вставки.
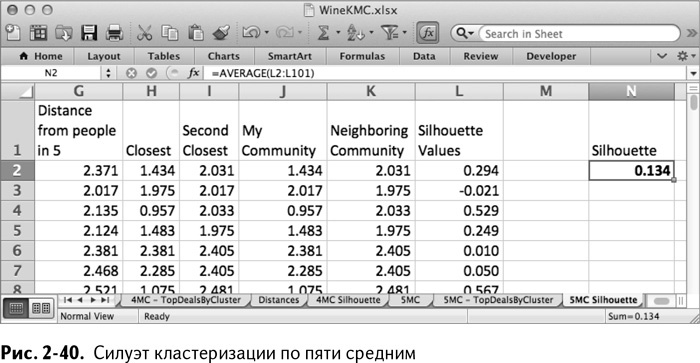
После исправлений лист должен выглядеть как на рис. 2-40.
Немного удручает, не правда ли? Силуэт не так уж и отличается. Наоборот, 0,134 даже хуже! Но это не назовешь неожиданностью после изучения получившихся кластеров. В обоих случаях получались 3 кластера, действительно имеющие смысл. Остальные – просто статистический шум. Может, стоит пойти в другом направлении и проверить k = 3? Если вы хотите дать этой гипотезе шанс, я оставлю это вам как самостоятельную работу.
Вместо этого предлагаю поразмыслить над тем, что мы делаем не так и откуда появляются эти непонятные кластеры, полные шума.
Назад: Девочки танцуют с девочками, парни чешут в затылке
Дальше: K-медианная кластеризация и асимметрическое измерение расстояний

