Чтобы более наглядно понять смысл теории гравитации Эйнштейна, вспомним теорию упругости, созданную британским ученым Робертом Гуком. Гук был одним из самых плодотворных научных деятелей XVII в. Он внес существенный вклад во впечатляющее количество научных областей и, кроме того, в течение долгого времени был секретарем Лондонского королевского общества. Его работы предвосхитили некоторые открытия Ньютона (касательно общих законов динамики и поведения 1 / r² закона тяготения). К сожалению для него, Ньютон, который был гением, но отличался весьма подозрительным и вспыльчивым нравом, игнорировал его достижения и делал все, чтобы принизить важность его работ. Наверное, Ньютон был бы в ярости, увидев такую интерпретацию теории гравитации Эйнштейна (вытеснившую его собственную), которую мы собираемся сделать, используя обобщение закона упругости Гука!

Отправная точка теории Гука довольно проста для понимания. Рассмотрим произвольную упругую структуру, т. е. такую, которая возвращается к своей первоначальной форме после деформирования воздействующей на нее силой. Простой пример упругой структуры – пружина. Рассмотрим пружину, верхний конец которой прикреплен к жесткому массивному телу, а нижний – свободен. Если потянуть вниз за нижний конец пружины или прикрепить к нему груз, то пружина деформируется и растянется. Если прикрепить не слишком тяжелый груз, то можно заметить, что растяжение пружины прямо пропорционально его весу: в два раза больший вес будет давать в два раза большее растяжение. Другими словами, деформация упругой структуры пропорциональна напряжению, действующему на эту структуру. Если обозначить «деформацию» буквой D, а «напряжение» буквой T, то закон упругости Гука сводится к простому утверждению D = κT, где κ – коэффициент пропорциональности, характеризующий «упругость» рассматриваемой структуры. Чем больше κ, тем более упругой является структура, т. е. тем больше она деформируется под действием заданного напряжения. Можно также сказать, что обратная коэффициенту κ величина 1 / κ измеряет жесткость рассматриваемой структуры. Чем меньше κ, тем больше жесткость (и тем меньше упругость). Этот универсальный закон упругости справедлив только в ограниченном диапазоне прикладываемого напряжения (не сильно отличным от нуля). Обратите внимание, что напряжения и соответствующие деформации могут прикладываться как в одном, так и в другом направлении, т. е. могут быть положительными или отрицательными. Независимо от знака приложенного напряжения, деформация будет возвращаться к нулю, если напряжение постепенно уменьшается до нуля. Это и есть основное свойство упругой структуры – стремление возвращаться в исходное «недеформированное» состояние, когда деформирующая сила перестает действовать.

В то же время если перейти определенный порог (так называемый «предел упругости»), другими словами, если приложить слишком большое напряжение, то в общем случае мы покинем область упругости для данной структуры. И тогда мы переходим в область «пластичности», где структура приобретает постоянную деформацию, остающуюся после того, как напряжение перестает действовать, и затем в область «разрыва», где структура рвется.

Чтобы немного развить интуицию, а также приблизиться к нашей модели «пространственно-временного желе», рассмотрим в качестве упругой структуры трехмерную среду, имеющую место в случае заливной телятины. То, что мы собираемся сказать, в равной степени относится и к более жесткой среде, такой как металл, однако жесткость металла настолько велика, что интуитивно сложно представить его в качестве упругой структуры. Поэтому мы рассматриваем кусок (однородного) желе. Деформируем этот блок, прикладывая давление, или напряжение, к его краям. Это создает напряженное состояние внутри куска. Такое напряженное состояние описывается (в механике сплошных сред) математическим объектом, называемым тензором напряжений. Этот тензор, который мы обозначим через T (от английского слова tension), позволяет вычислять силы внешнего воздействия, действующие на поверхность выделенного элемента объема внутри среды. В газообразной среде T определяется давлением газа.

Нам остается описать, как определяется деформация блока желе D. Когда деформация D мала, она определяется как разница между геометрической структурой деформированного и исходного недеформированного блока. Каким же образом можно измерить геометрическую структуру сплошной среды? Точно так же, как мы поступали выше, анализируя геометрическую структуру пространства при помощи визуализации. Опишем сначала визуализацию геометрии недеформированного блока желе (рассматриваемого в обычном евклидовом пространстве), представляя вокруг каждой точки блока геометрическое место точек, расположенных от данной на единичном расстоянии. Это дает регулярную сеть сфер внутри блока. Теперь мы деформируем блок, т. е. заставляем желе двигаться произвольным, но непрерывным образом (так же как деформируется содержимое тюбика зубной пасты, когда его сжимают). Это непрерывное перемещение деформации желе будет деформировать сеть сфер. Сначала центр каждой сферы смещается. Однако такой эффект сам по себе не связан с напряжением в среде, так как можно было бы, например, переместить весь блок желе вправо на один сантиметр, двигая его целиком и не создавая никакой нагрузки внутри блока. С точки зрения упругости важно, таким образом, измерить, как деформируется каждая сфера, когда она следует за движением желатина вокруг себя. Если рассматривать, как мы делаем здесь, небольшие смещения, то можно обнаружить, что сфера деформируется в «эллипсоид», т. е. в своего рода мяч для регби. Поэтому мы будем называть деформацией D математический объект, который измеряет разницу между эллипсоидом и сферой. Видно, что этот объект имеет ту же математическую природу, что и объект, описывающий наличие напряжений в среде, и, таким образом, является тензором, который называют тензором деформации. Наконец, закон упругости для однородной и изотропной сплошной среды, такой как блок желе, можно получить, если записать наиболее общее линейное соотношение, которое может существовать между двумя математическими объектами одного и того же типа (тензором деформации D и тензором напряжений T): D = κT.

Немного расширив понимание упругости непрерывной среды (в смысле обычной механики), мы можем вернуться к главной цели этой главы: попытке понять общую теорию относительности как теорию упругости пространства-времени. Для этого необходимо обсудить два вопроса: (i) что является аналогом D, т. е. какой математический объект описывает «деформацию» пространства-времени по отношению к «однородному» пространству-времени Минковского; и (ii) что является аналогом T или, другими словами, какой математический объект описывает причину (или источник) пространственно-временной деформации, т. е. то, без чего пространство-время оставалось бы пространством-временем Минковского. Ответ на вопрос (ii) довольно быстро был получен Эйнштейном путем следующего рассуждения.

Во-первых, Эйнштейн предложил идентифицировать метрический тензор g, описывающий пространственно-временную хроногеометрию, с гравитационным полем. Этот вывод следовал из анализа принципа эквивалентности, открытого Эйнштейном в ноябре 1907 г. Рассмотрим, например, простой случай пространства-времени Минковского. Если наблюдатель исследует пространство-время Минковского, оставаясь при этом в «инерционной» системе отсчета, т. е. в системе, движущейся без ускорения, он не будет наблюдать гравитационное поле (свободные частицы не будут «падать», но будут оставаться в покое или же двигаться с постоянной скоростью), и метрический тензор g, описывающий пространственно-временную хроногеометрию будет тривиальным (т. е. будет задаваться постоянными коэффициентами). В то же время наблюдатель, находящийся в ускоряющемся лифте, т. е. использующий координаты, нелинейно связанные с обычными координатами специальной теории относительности, наблюдает два взаимосвязанных явления: (i) метрический тензор g приобретает более сложное выражение с коэффициентами, которые изменяются от одной точки к другой, и (ii) в ускоряющемся лифте возникает кажущееся гравитационное поле, т. е. частицы в нем как будто падают с ускорением. Это ускорение кажущегося притяжения напрямую связано с тем, что коэффициенты g меняются от одной точки к другой.

Осознав, что g = хроногеометрия = гравитация, перейдем к следующему этапу, состоящему в понимании того, что является источником g и тем самым источником гравитации. Со времен Ньютона известно (из-за универсальности свободного падения и равенства действия и противодействия), что масса определяет и то, как действует гравитация (определяя вес), и то, что создает гравитационное поле. Таким образом, источником гравитационного поля по Ньютону является масса. Однако, как говорилось в главе 2, специальная теория относительности полностью изменила и обогатила понятие массы. А именно: оно было заменено понятием массы-энергии – величины, сохраняющейся при любых преобразованиях, в ходе которых в силу уравнения E = mc2 масса может преобразовываться в энергию, и наоборот. В связи с этим Эйнштейн ожидал, что в качестве источника гравитации будет выступать масса-энергия, распределенная во всем пространстве-времени. Наш поиск источника гравитации, однако, не может считаться законченным, поскольку более детальный анализ причин сохранения массы-энергии на основе специальной теории относительности показывает, что плотность массы-энергии на единицу объема является лишь одной из компонент более сложного математического объекта, называемого тензором энергии-импульса. Этот тензор имеет 10 компонент: одна компонента описывает плотность массы-энергии на единицу объема, еще три описывают плотность импульса (или количества движения) на единицу объема, а остальные шесть описывают тензор напряжений в том же смысле, как введенный нами ранее тензор напряжений для трехмерной сплошной среды. Этот десятикомпонентный тензор, одновременно задающий как плотность массы (являющейся предметом закона Ньютона), так и тензор напряжений (являющейся предметом закона Гука), мы будем обозначать далее через T.

Вернемся к одному из наиболее важных моментов на пути к созданию Эйнштейном общей теории относительности. Как мы уже говорили, первая идея обобщения этой теории возникла у Эйнштейна в 1907 г., когда он все еще работал (по восемь часов в день, включая субботы) в бернском патентном бюро. Однако вскоре в связи с большим интересом к специальной теории относительности 1905 г., а также к некоторым другим его работам сразу несколько научных центров предложили Эйнштейну университетские позиции. В 1909 г. он оставил патентное бюро Берна, чтобы занять должность ассоциированного профессора в университете Цюриха (с той же зарплатой, которую он имел в Берне). Эйнштейн и Милева были счастливы вернуться в Цюрих – город, где они встретились во время учебы в Политехническом университете. Там в 1910 г. родился их второй сын Эдуард. Однако в 1911 г. Эйнштейн принял другой пост, на этот раз в качестве полного профессора, в немецком университете Праги. В Праге он провел лишь один год. Там он посещал литературный салон Берты Фант и встречался с (еврейскими) писателями и мыслителями Праги, в частности с Максом Бродом и Францем Кафкой. Именно в Праге он возобновил (поскольку в 1907–1911 гг. в основном занимался развитием своих квантовых идей, см. ниже) поиски обобщенной теории относительности и получил несколько очень важных результатов. В частности, он более точно понял принцип эквивалентности и пришел к идее о том, что этот принцип влечет наблюдаемое отклонение световых лучей, проходящих вблизи контура Солнца, и сдвиг в красную (более низкочастотную) часть спектра световых лучей, испускаемых с поверхности массивного тела (такого как Солнце).

В конце июля 1912 г. Эйнштейн с семьей возвращается в Цюрих, поскольку принимает должность полного профессора в своем родном Политехническом университете, который завоевал к тому времени более высокий титул Швейцарского федерального технологического института (Eidgenössische Technische Hochschule – ETH). Вероятно, именно в Цюрихе примерно в августе 1912 г. Эйнштейн сделал свой очень важный концептуальный «шаг» в построении общей теории относительности. Он, в сущности, понял то, что мы уже объясняли выше, а именно: (i) что гравитационное поле эквивалентно деформации геометрии пространства-времени и, следовательно, должно описываться 10 компонентами «хроногеометрического тензора» g; (ii) что источником «поля g» является распределение массы-энергии, импульса и напряжения, описываемое объектом с 10 компонентами – тензором энергии-импульса T; и, наконец, (iii) что основное уравнение релятивистской гравитации должно иметь форму закона упругости пространства-времени: D(g) = κT, где D(g) является математическим объектом, сконструированным из g и призванным описывать деформацию пространства-времени или, другими словами, определять насколько пространство-время, имеющее геометрию, описываемую g, отличается от пространства-времени Минковского.

С такими мыслями Эйнштейн отправился к своему старому другу Марселю Гроссману, который был его товарищем еще со времен учебы в ETH (тогда еще бывшего Политехом) и который много раз «спасал его», сначала предоставляя свои конспекты лекций перед экзаменами, затем помогая устроиться в патентное бюро Берна и, наконец, делая все, чтобы ETH предложил Эйнштейну пост заслуженного профессора. Марсель Гроссман был математиком, в 1907 г. он стал профессором геометрии в ETH, а с 1911 г. – деканом факультета математики и физики. Эйнштейн предложил Гроссману сотрудничество в поисках «хорошего определения» математического объекта D(g). Гроссман преподавал в ETH геометрию, и его математические работы также были сосредоточены на проблемах геометрии, но это была другая геометрия – геометрия структур, определяемых как множества прямых линий и точек в однородных пространствах. Гроссман не был знаком с тем типом «неоднородной» геометрии, которая требовалась Эйнштейну. Тем не менее, просмотрев математическую литературу, он быстро понял, что некоторые работы Римана, Кристоффеля, Риччи и Леви-Чивита несомненно содержали математические инструменты, необходимые и достаточные для построения объекта D(g), который искал Эйнштейн. Однако эти математические инструменты были довольно сложны, и, чтобы освоить их, а также понять их физический смысл, Эйнштейну и его другу приходилось прикладывать серьезные усилия в течение многих месяцев (а в случае Эйнштейна – многих лет). Приведем выдержку из письма Эйнштейна своему коллеге Арнольду Зоммерфельду, написанного в период, когда Эйнштейн прилагал «буквально сверхчеловеческие» усилия (используя его выражение) для решения проблемы релятивистской теории гравитации:

«Сейчас я работаю исключительно над проблемой гравитации, и я думаю, что с помощью моего здешнего друга-математика, мне наконец удастся преодолеть все трудности. Однако одно точно – никогда прежде я не испытывал таких мучений, работая над какой-либо проблемой. Я проникаюсь все большим уважением к математическим методам, поскольку прежде обычно рассматривал сложные математические методы как бесполезную роскошь! По сравнению с настоящей проблемой специальная теория относительности была просто детской игрой».

Действительно, Эйнштейн столкнулся с неожиданными техническими трудностями, которые не позволили ему с Гроссманом полностью разобраться с этой проблемой, т. е. построить искомый объект D(g). Тем не менее они подошли весьма близко к этой цели и рассматривали кандидата на роль D(g), который был, по существу, правильным, но которого Эйнштейн все же отверг из-за кажущегося конфликта между постулированным им принципом общей теории относительности и принципом причинности. Это стоило Эйнштейну еще трех лет «буквально сверхчеловеческой» работы, прежде чем он наконец нашел окончательное решение в ноябре 1915 г. в Берлине. Эйнштейн покинул Цюрих и ETH в 1914 г., чтобы занять пост директора по исследованиям без преподавательских обязанностей в Прусской академии наук в Берлине. Этот пост был создан специально для него, в частности, по инициативе Макса Планка, который, как мы уже видели выше, был первым физиком высшего уровня, осознавшим, что специальная теория относительности по сути является грандиозной концептуальной революцией, сравнимой по размаху с революцией Коперника.

В заключение этой главы, я попрошу еще немного терпения у читателя, конечно же, утомленного долгой дискуссией, посвященной описанию геометрии «искривленного» пространства-времени посредством 10-компонентного объекта g и поиску 10-компонентного объекта D(g), измеряющего деформацию, связанную с g. (Последняя определяется по отношению к недеформированному случаю геометрии Минковского.) Если читатель представит себе, что Эйнштейн должен был в течение пяти лет подряд (1911–1915) непрерывно и настойчиво пытаться вновь и вновь разобраться с этой проблемой, то он, возможно, согласится потратить еще несколько минут, чтобы открыть для себя интуитивное ощущение одного из самых высоких достижений человеческой мысли. Я надеюсь, что на самом деле читатель этой книги вряд ли согласится с мнением, высказанным Ханнесом Альфвеном по случаю празднования 100-летнего юбилея со дня рождения Эйнштейна:

«Многие, наверное, почувствовали бы облегчение, узнав, что истинная природа физического мира может быть осознана не иначе как Эйнштейном или некоторыми другими гениями. Как это ни парадоксально, вполне возможно, что широкая общественность признала Эйнштейна не потому, что он был великим мыслителем, но потому, что он освободил всех и каждого от обязанности думать».

Математические исследования Римана и его последователей (Кристоффеля, Риччи и Леви-Чивита) общей пространственной (или пространственно-временной) геометрии выявили несколько математических объектов, характеризующих разницу между «деформированным» пространством (часто называемым «искривленным») и жестким, однородным пространством (называемым «плоским»). Визуально проблема состоит в том, чтобы описать «разницу» между рис. 3 и 8. Вопреки тому, что можно ожидать в наивном подходе (который является достаточным в более простом случае деформации блока желатина), оказывается недостаточно взять разницу в каждой точке между метрическим тензором g деформированной геометрии и простым выражением (со значениями 1 либо –1) этого тензора в недеформированном пространстве (или пространстве-времени). Действительно, мысленный эксперимент с лифтом Эйнштейна показывает, что если используется ускоряющаяся система отсчета (а также, как заметил Эйнштейн, вращающаяся система), то метрический тензор, описывающий хроногеометрию пространства-времени Минковского в такой системе отсчета, принимает довольно сложную форму с коэффициентами g, которые изменяются от точки к точке.

Теперь мы можем вернуться к первоначальной формулировке «самой счастливой мысли» в жизни Эйнштейна. Представим себя в произвольном пространстве-времени, деформированном присутствием материи и напряжения и снабженном нетривиальным метрическим тензором g, и представим свободно падающий лифт в этом пространстве-времени. Первоначальная идея состояла в том, что гравитационное поле исчезает внутри такого свободно падающего лифта, т. е. исчезает в задаваемой стенками лифта системе отсчета (рис. 6). Вопрос в том, полностью ли оно исчезает. Оказывается, что нет, так как два объекта, расположенные внутри лифта, не падают с абсолютно одинаковым ускорением. В самом деле, не находясь в одной и той же точке пространства(-времени), они будут иметь немного разные гравитационные ускорения (отличные также от ускорения падения самого лифта, зависящего от положения центра масс лифта). Таким образом, внутри свободно падающего лифта продолжает существовать небольшой остаток гравитационного поля: та часть, которая не исчезает благодаря падению лифта в силу вариаций гравитационного поля от точки к точке.

Если бы мы находились в рамках ньютоновского описания гравитации, то этот неисчезающий остаток можно было бы связать с тем, что называется «силой прилива». Такое название происходит из следующего факта: Луна (как и Солнце) оказывает гравитационное притяжение на Землю (так же как Земля оказывает гравитационное притяжение на Луну). Поэтому Земля «падает» на Луну (и на Солнце), и наоборот. Земля, следовательно, естественным образом представляет лифт в свободном падении. Падение Земли на Луну компенсирует большую часть ускорения, создаваемого Луной. Представим теперь, что океаны покрывают всю поверхность Земли. Часть океана, расположенная со стороны Луны, будет притягиваться к Луне сильнее, чем центр масс Земли, который, в свою очередь, будет притягиваться сильнее, чем часть океана, расположенная на противоположной от Луны стороне. Поэтому на свободно падающей Земле наблюдается остаточный эффект, который поднимает океан со стороны Луны и который поднимает океан на противоположной стороне Земли, еще более удаляя его от Луны. Этот эффект, который поднимает две части океана на противоположных сторонах, является причиной приливов и отливов (которые, таким образом, определяются двумя остатками гравитационных полей, создаваемых Луной и Солнцем в системе отсчета, связанной с падающей Землей).

Математическая теория (основанная Риманом), описывающая не полностью исчезающий остаток хроногеогравитационного поля g в свободно падающей системе отсчета, привела к возникновению математического объекта, содержащего 20 компонент, – тензора Римана – Кристоффеля R. Это своего рода обобщение «приливного тензора» ньютоновской гравитации дает наиболее полноценное описание истинной локальной деформации искривленного пространстве-времени. Однако этот тензор не мог быть искомым математическим объектом, который требовался Эйнштейну и который должен был иметь лишь 10 компонент, как и его источник T. После долгих колебаний и сомнений Эйнштейн понял в ноябре 1915 г., что существует только один способ построения объекта с 10 компонентами исходя из R, описывающего пространственно-временную деформацию и удовлетворяющего как принципу общей теории относительности, так и закону сохранения энергии и импульса. Этот 10-компонентный объект, который мы обозначаем D(g), называется «тензором Эйнштейна». Таким образом, после восьми лет исследований ему, наконец, удалось написать «уравнения гравитации Эйнштейна»: D(g) = κT, где 10 величин в левой части уравнения описывают (частично) локально измеримую деформацию пространственно-временной хроногеометрии, тогда как 10 величин справа содержат источник этой деформации – распределение напряжения и распределение импульса и массы-энергии. Как мы уже говорили, эти 10 уравнений, связывающих деформации в присутствии приложенных внутри среды напряжений, аналогичны базовым уравнениям, описывающим упругость не сильно деформированной среды.

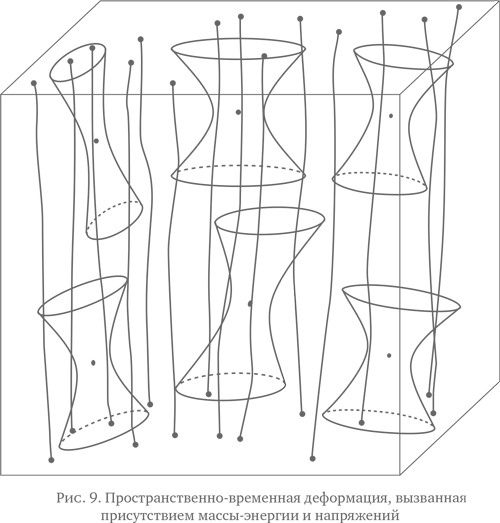
Рисунок 9 иллюстрирует содержание уравнений гравитации Эйнштейна. Присутствие здесь массы-энергии представлено с помощью мировых линий (или пространственно-временных линий), которые оставляют частицы в пространстве-времени. Отметим «волокнистый» характер изображенного на рисунке распределения массы-энергии. Присутствие этого распределения приводит к деформации геометрии пространства-времени, изображенного посредством набора деформированных песочных часов.