Книга: Далекое будущее Вселенной Эсхатология в космической перспективе
Назад: 7. Экзотические генетические материалы и распространенность жизни во Вселенной
Дальше: 9. Жизнь во Вселенной Цифровая или аналоговая?
8. Время без конца
Физика и биология в открытой вселенной
Фримэн Дж. Дайсон
Приведены количественные оценки трех классов феноменов, способных возникнуть в открытой космологической модели фридманновского типа. (1) Нормальные физические процессы, происходящие в течение очень долгих сроков. (2) Биологические процессы, возникающие в результате адаптации жизни к низким температурам в соответствии с постулированным нами законом масштабирования. (3) Радиокоммуникация между формами жизни, существующими в различных частях вселенной. Общее заключение этого анализа — открытую вселенную не обязательно ждет конечное состояние вечного покоя. Если предполагаемые градационные законы масштабирования верны, то жизнь и коммуникация, используя ограниченное количество энергии, могут существовать вечно.
Лекция I. Философия
Год назад Стивен Уэйнберг опубликовал замечательную книгу «Первые три минуты» (Weinberg, 1977); в ней он рассказывает широкой публике о том, каково состояние наших знаний о рождении вселенной. В шестой главе книги он подробно описывает, каким образом на пути наблюдения и изучения вселенной встала робость наших теоретиков:
Такое часто случается в физике: наша ошибка не в том, что мы слишком серьезно относимся к своим теориям, а в том, что не принимаем их всерьез. Нелегко в полной мере осознать, что цифры и уравнения, с которыми мы играем у себя за столом, имеют какое-то отношение к реальному миру. Хуже того, порой, кажется, возникает какое-то молчаливое соглашение о том, что определенные феномены просто не годятся для серьезного теоретического и экспериментального изучения. Альфер, Герман и Гамов (1948) заслуживают величайшего уважения прежде всего за то, что вообще решились серьезно рассмотреть вопрос о новорожденной вселенной и попытались понять, какие из известных нам физических законов применимы к первым трем минутам ее существования. Но даже они не сделали последнего шага — не убедили радиоастрономов поискать микроволновый радиационный фон. Самый важный из результатов, достигнутых открытием радиационного фона с температурой 3°К (Пенсиас и Уилсон, 1965): оно наконец заставило людей всерьез задуматься о том, что ранняя вселенная действительно существовала.
Благодаря Пенсиасу и Уилсону, Уэйнбергу и другим, изучение начала вселенной в наше время считается вполне серьезным и уважаемым занятием. Профессиональным физикам, занятым первыми тремя минутами — или первой микросекундой — больше не приходится смущаться, говоря о своей работе. А вот с концом вселенной все обстоит совсем по–другому. Разыскивая литературу по этой теме, я нашел всего несколько статей (Rees, 1969; Davies, 1973; Islam, 1977 и 1979; Barrow and Tipler, 1978). Разумеется, список не полон. Однако в этих статьях поражает их извиняющийся или шутливый тон, как будто сами авторы умоляют не принимать их всерьез. В наше время исследование отдаленного будущего предстает таким же сомнительным занятием, каким было тридцать лет назад исследование далекого прошлого. Я в особенном долгу перед Джама–лем Исламом за черновик его статьи, опубликованной в 1977 году, который впервые заставил меня серьезно задуматься об отдаленном будущем. Надеюсь, эти мои лекции приблизят наступление дня, когда эсхатология, наука о конце вселенной, из раздела богословия превратится в серьезную и уважаемую научную дисциплину.
Сам Уэйнберг не избежал предрассудков, которые я стараюсь развеять. В конце своей книги, посвященной прошлому вселенной, он дает краткое приложение, касающееся ее будущего. Первые три минуты он описывает на ста пятидесяти страницах, а всему, что ждет нас дальше, отводит всего пять страниц. Если оставить в стороне технические подробности, его взгляд на будущее выражается одной фразой:
Чем понятнее для нас вселенная, тем бессмысленнее она нам представляется.
Здесь Уэйнберг, возможно сам того не желая, указывает на реальную проблему. Невозможно детально описать долгосрочное будущее вселенной, не учитывая влияния жизни и разума. Невозможно вычислить способности жизни и разума, не затрагивая хотя бы вскользь философских вопросов. Если мы хотим понять, как может разумная жизнь использовать физическое развитие вселенной в своих собственных целях, нам не удастся полностью избежать вопроса о том, каковы могут быть ценности и цели разумной жизни. Но стоит упомянуть слова «ценность» и «цель» — и мы на полном ходу врезаемся в одно из жесточайших табу, установленных наукой XX века. Послушаем, что говорит Жак Моно (1970), первосвященник научной рациональности, в своей книге «Случайность и необходимость»:
Всякое смешение знания с ценностями незаконно и недопустимо.
Моно — один из основателей молекулярной биологии. Страшно подпадать под его анафему. И все же я рискну с ним поспорить и других постараюсь подвигнуть на то же самое. Табу на смешение знания с ценностями пришло к нам из XIX века, из великой битвы между биологами–эволюционистами во главе с Томасом Гексли и церковниками под предводительством епископа Уилберфорса. Гексли битву выиграл, но и сто лет спустя Моно и Уэйнберг все еще сражались с призраком епископа Уилберфорса. В наше время у физиков нет причин опасаться этого призрака. Если анализ отдаленного будущего приведет нас к вопросам, связанным с темами конечного смысла и цели жизни — давайте исследовать эти вопросы смело и без стеснения. И что за беда, если наши ответы на эти вопросы окажутся наивными и незрелыми? Значит, наука по–прежнему жива — и ей есть куда двигаться.
В этих лекциях я постараюсь исследовать будущее так же, как Уэйнберг в своей книге исследовал прошлое. Мои высказывания будут просты, даже примитивны, но неизменно подкреплены цифрами. Моя цель — установить количественные параметры судьбы вселенной. Извиняться за то, что смешиваю философские рассуждения с математическими уравнениями, я не собираюсь.
Две простейшие космологические модели (Weinberg, 1972) описывают универсальную вселенную с нулевым давлением, открытую или закрытую. Геометрия закрытой вселенной описывается уравнением
ds2 = R2[dψ2 — dχ2 — sin2χdΩ2], (1)
где χ — пространственная координата, движущаяся вместе с материей, ψ — временная координата, связанная с физическим временем t по формуле:
t = Т0 (ψ — sinψ), (2)
a R — радиус вселенной, заданный по формуле:
R = сТ0 (1 — cosψ), (3)
Вселенная в целом представлена в системе пространственно–временных координат (ψ, χ) как конечный прямоугольный параллелепипед:
О< ψ< 2π, 0< χ< π. (4)
Вселенная замкнута как в пространстве, так и во времени. Общая ее протяженность —
2πТ0, (5)
где Т0 — в принципе измеряемое количество. Если наша вселенная описывается этой моделью, значение Т0 должно составлять, как минимум, 1010 лет.
Простейшая модель универсальной открытой вселенной с нулевым давлением описывается уравнением:
ds2 = R2[dψ2 — dχ2 — sinh2χdΩ2], (6)
где
t = T0 (sinnψ — ψ), (7)R = cT0 (coshψ — 1), (8)
а координаты (?; ?) простираются в бесконечность:
О< ψ< ∞, 0< χ< ψ (9)
Открытая Вселенная определена сразу в пространстве и во времени.
Модели (1) и (6) — это лишь простейшие из возможностей. В литературе можно найти множество иных, куда более сложных моделей. Но для наших целей достаточно обсудить (1) и (6) как примеры открытой и закрытой вселенных. Вопрос о том, является ли наша вселенная открытой или закрытой, можно разрешить только наблюдением. Этого вопроса я больше касаться не буду, замечу лишь, что мои философские убеждения свидетельствуют в пользу открытой вселенной, и имеющиеся у нас данные наблюдений не исключают этой возможности (Gott, Gunn, Schramm, and Tinsley, 1974 и 1976).
Обычно считается (Weinberg, 1977), что открытую и закрытую вселенные ждет равно печальное будущее. Согласно этому мнению, выбор у нас невелик — поджариться в закрытой вселенной или замерзнуть в открытой. Конец закрытой вселенной детально описан Ризом (1969). К сожалению, приходится согласиться с Ризом в том, что в этом случае избежать превращения в жаркое нам не удастся. Как бы глубоко мы ни зарывались в землю в надежде спастись от всевозрастающей ярости фоновой радиации голубого смещения, самое большее, что нам удастся, — отсрочить на несколько миллионов лет свой прискорбный конец. Не буду подробно обсуждать случай закрытой вселенной — мысль о том, что все наше бытие заперто в ящике с параметрами (4), вызывает у меня клаустрофобию. Коснусь лишь одного вопроса, дающего нам призрачный шанс на выживание. Предположим, мы выяснили, что вселенная от природы закрыта и приговорена к уничтожению. Что, если благодаря вмешательству разума, например, превращая материю в излучение и заставляя энергию двигаться в определенном направлении, мы сумеем прорвать стены закрытой вселенной и изменить топологию пространства–времени таким образом, что лишь часть ее погибнет, а другая часть будет расширяться вечно? Ответа на этот вопрос я не знаю. Но, если выяснится, что наша вселенная закрыта, у нас останется примерно 1010 лет на исследование возможности такого «технологического прорыва».
Меня интересует в первую очередь открытая космология, поскольку она предоставляет гораздо больше возможностей для деятельности жизни и разума. В открытой космологии горизонты расширяются до бесконечности. Говоря точнее, расстояние до горизонта в модели (6) равно
d = Rψ, (10)
где R задано (8), а количество видимых в этом горизонте галактик составляет
N = N0 (sinh2ψ — 2ψ), (11)
где N0 — это число порядка 1010.
Сравнив (11) с (7), мы видим, что количество видимых галактик в далеком будущем варьируется в пределах t2. Это происходит благодаря той любопытной числовой закономерности, что угловой размер типичной галактики во время t составляет
5~ 105t-1rad, (12)
где t измеряется в годах. Поскольку (11) и (7) дают
N ~ 10–10t2, Nδ2 ~ 1, (13)
оказывается, что, как бы далеко в будущее мы ни заглянули, небо всегда будет заполнено галактиками. По мере того, как видимые размеры каждой галактики уменьшаются, на горизонте появляются новые галактики, заполняющие пустоты. Свет от далеких галактик будет иметь сильное красное смещение. Однако, если со временем мы сумеем приспособить свое зрение ко все более и более длинным световым волнам, небо никогда не станет для нас пустым и темным.
Говоря об открытой вселенной, описываемой формулой (6), хотелось бы обсудить три принципиальных вопроса:
1. Верно ли, что по мере своего расширения и остывания эта вселенная замерзнет до состояния полного физического покоя?
2. Возможно ли в открытой вселенной бесконечное выживание жизни и разума?
3. Возможно ли поддерживать коммуникацию и передавать информацию при все увеличивающемся расстоянии между галактиками?
Эти три вопроса мы подробно обсудим в лекциях 2, 3 и 4. Я собираюсь ответить на них «нет», «да» и «может быть». Возможно, эти ответы — лишь отражение моих оптимистических философских предубеждений. Я не жду, что все с ними согласятся, и хочу лишь того, чтобы люди начали серьезно размышлять на эти темы.
Если, как я надеюсь, мои ответы окажутся верны, что это означает? Это будет означать, что мы открыли в физике и астрономии некий аналог теоремы Геделя (1931) в математике. Гедель доказал [см. Нейджел и Ньюман (1956)], что мир чистой математики неистощим: не существует конечного набора аксиом и правил, исчерпывающих всю математику; в пределах каждого конечного набора аксиом мы можем найти важные математические вопросы, на которые эти аксиомы не отвечают. Надеюсь, такая же ситуация существует и в мире физики. Если мое представление о будущем верно, это означает, что мир астрономии и физики также неистощим; как бы далеко в будущее мы не заглянули, в нем всегда происходит нечто новое: поступает новая информация, открываются для исследования новые миры, постоянно расширяется область владений жизни, сознания и памяти.
Рассуждая таким образом, я смешиваю знание с ценностями и нарушаю запрет Моно. Однако я не первый. До эпохи Дарвина, Гексли и епископа Уилберфорса, в восемнадцатом столетии, ученые не чурались смешения науки с ценностными суждениями. Когда Томас Райт (1750), первооткрыватель галактик, объявил о своем открытии, его не смутила возможность использовать в поддержку астрономической теории богословский аргумент:
Поскольку, возвеличивая творение, мы возвеличиваем и Творца, то, памятуя о его бесконечности и бесконечной творящей силе, благочестиво будет заключить, что, как видимое творение полно созвездий и планетарных миров, так и бесконечная глубина являет неисчислимое множество творений, подобных нам известным… О том, что это истина, свидетельствуют едва различимые туманные точки, расположенные вдали от известных нам созвездий, на таком расстоянии, откуда не мог бы долететь до нас свет звезды или иного небесного тела; весьма вероятно, что это иные тварные миры, граничащие с нашим, но столь отдаленные, что до них не достигают даже наши телескопы.
Тридцать пять лет спустя рассуждения Райта были подтверждены точными наблюдениями Уильяма Гершеля. Кроме того, Райт вычислил количество пригодных для обитания миров в нашей галактике:
В целом число их должно составлять 170 000 000, не считая комет, которые, по моему суждению, являются самыми многочисленными из небесных тел тварного мира.
Утверждение Райта о кометах, возможно, тоже верно, хотя он и не сообщает, как определил их численность. Существование такого количества пригодных для обитания миров для него не только научная гипотеза, но и предмет моральной рефлексии:
В этом великом небесном творении гибель одного мира, такого, как наш, или даже полное уничтожение системы миров может означать для великого Творца Природы не более, чем для нас — самое обычное жизненное происшествие; и весьма вероятно, что такие последние и окончательные Судные дни случаются здесь не реже, чем у нас на земле — дни рождения или смерти. В этой мысли есть нечто столь ободряющее, что всякий раз, возводя глаза к небу, я спрашиваю себя, почему бы всем нам не стать астрономами; ибо если бы люди, наделенные умом и здравым смыслом, не пренебрегали наукой, к коей влекут их естественные устремления, то понимание природы убедило бы их в собственном бессмертии и научило со спокойствием и бесконечным терпением переносить все неприятности, присущие человеческой природе.Наблюдение за звездным небом подсказывает нам, чего не следует делать, чтобы сохранить свое природное право на это драгоценное достояние, которое, увы, мы воображаем принадлежащим нам безраздельно, как некоей расе тщеславных гигантов, хотя на деле мы бесконечно малы и прикованы к своему миру, как к малой песчинке приковано множество атомов песка.
Такова мудрость восемнадцатого столетия. «Чем лучше мы понимаем вселенную, тем более бессмысленной она нам представляется», — отвечает на это Стивен Уэйнберг. Что ж, если это мудрость нынешнего века, я предпочту век давно минувший.
Лекция II. Физика
В этой лекции я вслед за Исламом (1977) разберу вопрос о физических процессах, происходящих в открытой вселенной на протяжении очень долгих временных периодов. При этом я говорю о естественной вселенной, не учитывая влияния на нее жизни и разума. Жизнь и разум мы обсудим в лекциях 3 и 4.
В основе нашего рассуждения лежат два предположения. (1) Законы физики не меняются со временем. (2) Все важные для нашей темы физические законы нам уже известны. Эти два предположения уже были выдвинуты Уэйнбергом (1977) в его описании прошлого. Я обосновываю их так же, как и он. Верим мы или нет, что ныне известные законы физики являются конечной и неизменной истиной — весьма полезно проследить следствия действия этих законов как в прошлом, так и в будущем. В экстраполяции наших знаний от известного к неизвестному лучше проявить излишнюю смелость, чем излишнюю робость. Может случиться, как уже случилось с космологическими рассуждениями Альфера, Германа и Гамова (1948), что наивное распространение известных нам законов на новую территорию приведет нас к постановке новых и важных вопросов.
В других местах (Dyson, 1972, 1978) я суммировал свидетельства в пользу того, что законы физики не меняются. Самое поразительное свидетельство недавно получено Шляхтером (1976) при измерении соотношений изотопов в образцах руды, взятой из естественного ядерного реактора, существовавшего около 2 миллиардов лет назад в урановой шахте Окло в Габоне (Maurette, 1976). Основное полученное им число — соотношение (149Sm/147Sm) между двумя легкими изотопами самария, не являющимися продуктами ядерной реакции. У нормального самария это соотношение составляет около 0,9; в реакторе Окло — около 0,02. По–видимому, количество 149Sm было сильно уменьшено дозой горячих нейтронов, воздействию которых этот изотоп подвергся во время ядерной реакции. Если в современном реакторе мы померим сечение захвата горячих нейтронов у 149Sm, то получим значение 55 kb, с сильным резонансом захвата при энергии нейтронов 0,1 eV. Детальный анализ соотношений изотопов в Окло приводит нас к выводу, что два миллиарда лет назад сечение 149Sm находилось в интервале 55 ± 8 kb. Это означает, что за 2∙109 лет значение резонанса захвата не сдвигалось более, чем на 0,02 eV. Однако положение этого резонанса соответствует различию между энергиями связи в основном состоянии 149Sm и в производном состоянии 150Sm, захватившем нейтрон. Каждая из этих энергий составляет порядка 109 eV и сложным образом зависит от силы ядерного и кулоновского взаимодействий. То, что на протяжении 2∙109 лет между этими энергиями связи сохраняется баланс с точностью 2 доли на 1011, показывает, что изменения величин ядерной и кулоновской сил не могли быть больше, чем несколько долей на 1018 в год. На сегодняшний день это наиболее убедительное доказательство неизменности законов физики. То, что никаких свидетельств изменений не обнаружено, разумеется, не доказывает, что законы строго постоянны. В особенности нельзя исключить возможности вариаций в величине гравитационных сил, причем во временной период гораздо короче, чем 1018 лет. Но для простоты мы примем, что законы физики строго постоянны. Всякое иное предположение создаст нам большие сложности, заставив вводить произвольные дополнительные гипотезы.
Доказать, что все физические законы, имеющие значение для отдаленного будущего, уже нам известны, для меня невозможно в принципе. Наиболее серьезный вопрос, касающийся конечной судьбы вселенной, — вопрос о том, абсолютно ли защищен протон от распада на более легкие частицы. Если протон нестабилен — вся материя смертна и обречена рассеяться в радиацию. Выдвигаются серьезные теоретические аргументы (Zeldovich, 1977; Barrow and Tipler, 1978; Feinberg, Goldhaber, and Steigman, 1978) в поддержку мнения, что протоны распадаются с большим периодом полураспада, возможно в ходе процессов, в которых задействуются черные дыры. Экспериментально установленные ограничения на распад протонов (Kropp and Reines, 1965) не исключают существования таких процессов. Однако опять-таки для простоты мы исключаем эту возможность и предполагаем, что протон абсолютно стабилен. Позже я подробно рассмотрю воздействие реальных процессов, задействующих черные дыры, на стабильность материи в целом.
Теперь я готов начать дискуссию о физических процессах, происходящих в открытой космологии (6) в течение все более и более продолжительных отрезков времени. Сначала рассмотрим классические астрономические процессы, затем — процессы квантовой механики.
Примечание, добавленное в гранках. Со времени публикации этих лекций вышло в свет множество статей, посвященных моделям «великого объединения» в физике элементарных частиц, где протон нестабилен (Nanopoulos, 1978; Pati, 1979; Turner and Schramm, 1979).
А. Эволюция звезд
Самые долгоживущие звезды с низкой массой истощат свое водородное «топливо», сожмутся в белых карликов и остынут до крайне низких температур за период порядка 1014 лет. Более тяжелым звездам понадобится меньше времени, чтобы дойти до финального состояния — белого карлика, нейтронной звезды или черной дыры, в зависимости от особенностей эволюции каждой конкретной звезды.
Б. Отделение планет от звезд
Среднее время, необходимое для того, чтобы планета отделилась от звезды в результате близкой встречи со второй звездой, составляет
Т = (pVσ)-1, (14)
где р — плотность звезд в пространстве, V — средняя относительная скорость двух звезд и σ — сечение столкновения, вызвавшего отделение. Для системы «Земля–Солнце», двигающейся во внешней области диска спиральной галактики, приблизительные количественные значения следующие:
р = 3∙10–41 км3, (15)V = 50 км/с, (16)σ = 2∙1016 км2, (17)Т= 1015 лет. (18)
Временной отрезок для встречи, влекущей за собой серьезные нарушения планетарных орбит, составляет заметно меньше, чем 1015 лет.
В. Отделение звезд от галактик
Динамическая эволюция галактик — сложный и еще не до конца понятный процесс. Здесь мы можем дать только очень грубую оценку сроков. Если галактика состоит из N звезд массой М в радиусе R, то их средняя скорость составляет порядка
V = [GNM/R]1/2. (19)
Сечение для близкой встречи двух звезд, заметно изменяющей направление их движения, составляет
σ = (GM/V2)2 = (R/N)2. (20)
Среднее время, проходящее для одной звезды между двумя столкновениями, составляет
Т = (ρVσ)1 = (NR3/GM)1/2. (21)
Если мы рассматриваем типичную крупную галактику, в которой N = 1011, а R = 3∙1017 км, то
Т= 1019 лет. (22)
Динамическая релаксация галактики происходит главным образом благодаря встречам звезд на значительном расстоянии друг от друга с характерным временем
TR = T(logN)-1 = 1018 лет. (23)
В результате объединенного эффекта динамической релаксации и близких столкновений центральные районы галактики коллапсируют в черную дыру, одновременно выталкивая звезды из внешних регионов. Выталкиваемые звезды достигают нужной скорости и отделяются от галактики по прошествии порядка 1019 лет. Мы не знаем, какая часть массы галактики в конце концов погибнет в черной дыре, а какая часть отделится от галактики. Возможно, отделившаяся масса в конечном счете будет составлять от 90 до 99 процентов.
Драматические события, наблюдаемые нами сейчас в центральных регионах многих галактик, возможно, вызваны подобным процессом динамической эволюции, происходящем в гораздо более краткосрочном режиме. Согласно (21), срок эволюции и коллапса может быть небольшим, если эволюционирующих объектов немного и они массивны, например, не отдельные звезды, а компактные скопления звезд и газовые облака. Долгие сроки эволюции (22) характерны для галактик, не содержащих в себе динамических объектов крупнее отдельных звезд.
Г. Разрушение орбит гравитационной радиацией
Если некая масса вращается вокруг фиксированного центра со скоростью V, периодом Р и кинетической энергией Е, она будет терять энергию под воздействием гравитационной радиации со скоростью порядка
Eg = (V/c)5 (Е/Р). (24)
Всякая гравитационно связанная система объектов, вращающихся друг вокруг друга, будет разрушена благодаря действию радиации в течение срока
Tg = (c/V)5 P. (25)
Для земли, вращающейся вокруг солнца, срок действия гравитационной радиации составляет
Tg= 1020 лет. (26)
Поскольку это гораздо дольше, чем (18), к тому времени, когда гравитационная радиация начнет действовать, земля почти наверняка будет оторвана от солнца. Однако, если случится, что солнце вместе с землей оторвется от галактики, скорее всего, в течение срока (26) земля сольется с солнцем.
Орбиты звезд в галактике также разрушаются под действием гравитационной радиации в течение срока (25), где Р в данном случае — период их галактических орбит. Для галактики типа нашей, в которой V = 200 км/с, а Р = 2,108 лет, срок составляет
Tg= 1024 лет. (27)
Это опять-таки гораздо дольше, чем (22), что показывает, что в эволюции галактик динамическая релаксация играет более важную роль, чем гравитационная радиация.
Д. Уничтожение черных дыр путем процесса Хокинга
По Хокингу (1975), всякая черная дыра массой М разрушается путем излучения термальной радиации и полностью исчезает по истечении срока, составляющего
Т = (G2M3/hc4). (28)
Срок жизни черной дыры с массой солнца —
Τ = 1064 лет. (29)
Срок жизни черных дыр с массой галактики простирается до 10100 лет. В конце жизни каждая черная дыра на небольшое время ярко вспыхивает. В последнюю секунду своего существования она излучает около 1031 эргов горячей радиации. Таким образом, холодная расширяющаяся вселенная будет время от времени освещаться фейерверками.
Е. При абсолютном нуле материя становится жидкой
Далее мне хотелось бы обсудить группу физических процессов, происходящих с обычной материей при абсолютном нуле в результате проницаемости квантово–механического барьера. Время действия этих процессов вычисляется по формуле Гамова:
Τ = exp(S)T0, (30)
где Т0 — период естественного колебания системы, a S — интеграл действия
S = (2/h) ∫ (2MU(x))1/2dx. (31)
Здесь х — координата, измеряющая состояние системы, проходящей через барьер, a U(x) — высота этого барьера как функция х. Чтобы получить примерную оценку S, я заменяю (31) следующей формулой:
S = (8MUd2/h2)"2, (32)
где d — толщина, U — средняя высота барьера, a M — масса объекта, который сквозь него проходит. Рассмотрим процессы, при которых значение S велико, что чрезвычайно увеличивает и их продолжительность (30).
В качестве примера возьмем поведение сгустка плотной материи — астероида или планеты, остуженного до абсолютного нуля. Благодаря силам сцепления и химической связи его атомы застывают в фиксированном положении, казалось бы, навсегда. Однако время от времени они двигаются и изменяют свое положение друг относительно друга, пересекая энергетические барьеры путем квантово–механического туннелирования. Высота барьера, как правило, порядка одной десятой единицы Риндберга:
U = (1/20) (e4m/h2), (33)
а плотность — порядка радиуса Бора:
d = (h2me2), (34)
где m — масса электрона. Таким образом, получаем интеграл действия
S = (2Amp/5m)1/2 = 27А1/2, (35)
где тр — масса протона, а А — атомный вес движущегося атома. Для атома железа, у которого А = 56, a S = 200, (30) дает
Т= 1065 лет. (36)
Даже самые прочные материалы не смогут сохранить свою форму или химическую структуру за временной период, сравнимый с (36). В период 1065 лет любой камень начнет вести себя как жидкость, под воздействием гравитации постепенно принимая сферическую форму. Его атомы и молекулы будут непрерывно перемешиваться, как молекулы в капле воды.
Ж. Вся материя превращается в железо
При абсолютном нуле в материи будут продолжаться как ядерные, так и химические реакции. Элементы тяжелее железа будут превращаться в железо посредством различных процессов, таких, как расщепление и альфа–излучение. Элементы легче железа будут соединяться путем реакций слияния ядер и постепенно также превращаться в железо. Рассмотрим, например, реакцию слияния, в которой два ядра, обладающие атомным весом 1/2А и зарядом 1/2Z, объединяются, образуя ядро (A, Z). Кулоновское взаимоотталкивание ядер эффективно экранируется электронами, пока они не приблизятся друг к другу на расстояние
d = Z-1/3 (h2/me2) (37)
Кулоновский барьер обладает толщиной d и высотой
U = (Z2e2/4d) = ¼Z7/3 (e4m/h2). (38)
Сокращенная масса для относительного движения двух ядер:
М = 4¼Amр. (39)
Тогда интеграл действия (32) получает значение
S = (½AZ5/3(mp/m))1/2 = 30A½Z5/6. (40)
Для двух ядер, вместе образующих железо, Z = 26, А = 56, S = 3500, и
Т= 101500 лет. (41)
В промежуток времени, описанный формулой (41), обычная материя радиоактивна и постоянно генерирует ядерную энергию.
З. Превращение железных звезд в нейтронные звезды
По истечении срока (41) большая часть материи во вселенной, в обычном состоянии находящаяся в форме звезд с низкой массой, превращается в белые карлики — холодные шары, состоящие из чистого железа. Но железная звезда — это еще не самое низкоэнергетическое состояние. Она может избавиться от огромного количества энергии, если превратится в нейтронную звезду. Чтобы коллапсировать, ей необходимо лишь преодолеть барьер конечной высоты и толщины. Интересно спросить, существует ли асимметричный коллапс, проходящий через более низкую седловую точку, чем симметричный коллапс. Я не смог найти приемлемую асимметричную форму, так что мы предполагаем, что коллапс имеет сферическую симметрию. В интеграле действия (31) координата х становится радиусом звезды, и интеграл берется от г, радиуса нейтронной звезды, до R, радиуса железной звезды, с которого начинается коллапс. Высота барьера U(x) будет зависеть от уравнения состояния материи, которое при близости х к г весьма неопределенно. По счастью, уравнение состояния материи хорошо известно для большей части отрезка интегрирования, когда х велико по сравнению с г и основной вклад в U(x) составляет энергия нерелятивистских дегенерирующих электронов:
U(x) = (N5/3h2/2mx2), (42)
где N — число электронов в звезде.
Интегрирование по х в (31) дает логарифм:
log(R/R0), (43)
где R0 — радиус, при котором электроны становятся релятивистскими и формула (42) перестает работать. Для звезд с низкой массой этот логарифм будет порядка единицы, а интеграл, соответствующий релятивистской области x<R0, будет тоже порядка единицы. Масса звезды —
M = 2Nmp. (44)
Я заменяю логарифм (43) на единицу и для интеграла действия (31) получаю оценку
S = N4/3 (8mp/m)1/2 = 120N4/3. (45)
Таким образом, временной срок по формуле (30) —
T = exp(120N4/3)T0. (46)
Для типичной звезды с низкой массой получаем
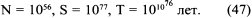
В формуле (46) совершенно неважно значение Т0, будь это ничтожная доля секунды или множество лет.
Мы не знаем, каждое ли превращение железной звезды в нейтронную звезду будет вызывать взрыв сверхновой. Во всяком случае, его результатом будет становиться мощный выброс энергии в форме нейтрино и другой, более скромный выброс энергии в форме рентгеновских лучей и видимого света. Таким образом, вплоть до самого конца срока, описанного в (47), вселенная будет освещаться фейерверками.
И. Превращение обычной материи в черные дыры
Долгий срок жизни (47) железных звезд верен лишь в том случае, если в ходе этого срока они не превратятся в черные дыры. Для коллапса любого сгустка материи в черную дыру верны те же формулы, что и для коллапса в нейтронную звезду. Единственная разница в том, что предел интегрирования в интеграле действия (31) теперь равен не радиусу нейтронной звезды, а радиусу черной дыры. Основная часть интеграла, происходящая из больших значений х, в обоих случаях одинакова. Таким образом, время коллапса материи в черную дыру задается формулой (46). Однако имеется важное изменение в значении N. Если возможны маленькие черные дыры, то превратиться в черную дыру может небольшая часть звезды. Сформировавшись, она в короткий срок поглотит остальную звезду. Срок коллапса звезды задается формулой:
T = exp(120NB4/3)T0, (48)
где NB — число электронов в куске железа, массой равном минимальной массе Мв черной дыры. Срок (48) таков же для любого сгустка материи массой больше Мв. Сгустки материи, обладающие массой меньшей, чем Мв, абсолютно стабильны. Подробную дискуссию о превращении материи в черные дыры см. у Harrison, Thorne, Wakano, and Wheeler (1965).
Числовое значение срока (48) зависит от значения Мв. Все, что мы знаем точно — это:
0≤МВ ≤МС, (49)
где
Мс = (hc/G)3/2mp-2 = 4∙1033g (50)
— это масса Чандрасекара. Черные дыры должны существовать для любой массы, большей Мс, поскольку звезды с массой, большей Мс, не имеют стабильного финального состояния и неминуемо должны коллапсировать.
Приведем четыре гипотезы, касающиеся Мв.
Мв = 0. Существуют черные дыры произвольно малой массы, и формула (48) бессмысленна. В этом случае вся материя нестабильна и должна коллапсировать в достаточно короткий срок, как предположил Зельдович (Zeldovich, 1977).
Мв равна массе Планка:
Мв = MPL = (hc/G)1/2 = 210–5g. (51)
Такое значение Мв предполагает теория излучения черных дыр, предложенная Хокингом (Hawking, 1975), согласно которой каждая черная дыра теряет массу, пока не достигнет массы порядка MPL, после чего исчезает во взрыве радиации. В этом случае формула (48) дает
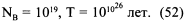
Мв равна квантовой массе:
MB=MQ = (hc/Gmp) = 3∙1014g, (53)
как предполагают Harrison, Thorne, Takano и Wheeler (1965). Здесь MQ — масса самой маленькой черной дыры, для которой имеет смысл классическое определение. Только для масс больше MQ физически оправдана формула преодоления барьера (31). Если мы принимаем (53), то
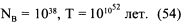
Мв равна массе Чандрасекара (50). В этом случае срок коллапса звезды в черную дыру будет того же порядка, что и срок коллапса в нейтронную звезду (47).
Долгосрочное будущее вселенной во многом зависит от того, какая из этих альтернатив верна. Если верно (iv), звезды могут превратиться в черные дыры, а затем рассеяться чистой радиацией, но массы планетарного размера будут существовать вечно. Если верно (iii), планеты также исчезнут в срок (54), но останутся стабильными материальные объекты массой до нескольких миллионов тонн. Если верно (ii), объекты размером с человека исчезнут в срок (52), но пылинки диаметром менее 100 μ будут существовать вечно. Если верно (i), исчезнут все материальные объекты без исключений, останется лишь радиация.
Если бы мне предложили выбрать самую вероятную альтернативу, я бы выбрал (ii). (iii) и (iv) кажутся мне маловероятными, поскольку противоречат теории Хокинга об излучении черных дыр. (i) представляется невероятной, поскольку трудно понять, почему протон, способный распасться, не может распасться быстро. Однако сейчас мы так мало знаем, что не можем исключать ни одной из этих четырех возможностей.
Таблица 1. Сроки протекания физических процессов

Результаты этой лекции суммированы в таблице 1. Этот список, в котором перечислены временные сроки физических процессов, не претендует на полноту. Несомненно, в те же и даже более продолжительные сроки могут происходить и многие другие физические процессы, не упомянутые мною. Основное заключение, которое я хотел вывести из своего анализа, следующее: насколько бы мы не заглянули в будущее, мы видим там какие-то события. В открытой космологии история не имеет конца.
Лекция III. Биология
Обращаясь к истории жизни в прошлом, мы видим, что на возникновение и развитие нового вида уходит около 10б лет, нового рода — около 107 лет, нового класса — около 108 лет, нового типа — около 109 лет; и, наконец, менее 10ю лет потребовалось на возникновение и развитие жизни в целом, от первых одноклеточных существ до homo sapiens. Если в будущем жизнь продолжит развиваться с той же скоростью, невозможно поставить пределы тому многообразию физических форм, которого она может достигнуть. Какие перемены, достойные встать рядом с переменами прошлого, принесут нам следующие 1010 лет? Вполне возможно, что за этот период жизнь сбросит с себя оболочку из плоти и крови и воплотится в межзвездном темном облаке (Hoyle, 1957) или в разумном компьютере (Čapek, 1923).
Перечислим основные вопросы, касающиеся природы жизни и сознания:
Что является основой сознания — материя или структура?
Возможны ли разумные темные облака (или компьютеры)?
Применимы ли в биологии законы масштабирования?
Мы не знаем, как ответить на эти вопросы. Но это не значит, что они не имеют ответов вообще. Вполне возможно, что прогресс в экспериментальной биологии позволит нам достаточно скоро найти ответы.
Позвольте мне подробнее остановиться на значении вопроса (i). Мое сознание каким-то образом связано с набором органических молекул у меня в голове. Вопрос в том, зависит ли существование моего сознания от этого конкретного набора молекул или только от их структуры. Иными словами, если создать копию моего мозга с той же структурой, но из другого материала, будет ли она думать, как я?
Если ответ на первый вопрос — «материя», значит, жизнь и сознание никогда не смогут оторваться от плоти и крови. В этом случае на вопросы (ii) и (iii) ответы отрицательные. Жизнь может существовать только в теплой среде, при наличии жидкой воды и достаточного количества свободной энергии, необходимой для поддержки постоянного уровня обмена веществ. В таком случае, поскольку запасы энергии в галактике конечны, конечно и существование жизни. По мере расширения и остывания вселенной запасы свободной энергии, требуемой жизнью для обмена веществ, неизбежно истощатся.
Поскольку я придерживаюсь оптимистической философии, то принимаю как рабочую гипотезу, что ответ на вопрос (i) — «структура». Это значит, что жизнь свободна принимать любое материальное воплощение, наилучшим образом отвечающее ее целям. Тогда, при утвердительных ответах на вопросы (ii) и (iii), становятся возможны количественные прикидки относительно будущего жизни во вселенной. Если выяснится, например, что материя защищена от превращения в черные дыры, только будучи раздроблена на пылинки по несколько микронов в диаметре, тогда, очевидно, наилучшей формой для существования жизни в отдаленном будущем станет нечто вроде «темного облака» Хойла: собрание пылевых частиц, обладающих положительными и отрицательными зарядами, самоорганизующихся и общающихся между собой с помощью электромагнитных сил. Мы не можем представить себе в деталях, как это облако будет поддерживать то состояние динамического равновесия, которое мы зовем жизнью. Но и архитектуру живой клетки протоплазмы мы никогда не смогли бы себе представить, если бы ее не увидели.
Чтобы предоставить конкретное описание того, как жизнь может адаптироваться к низким температурам, мне необходимо вывести закон масштабирования, независимый от конкретного материального воплощения жизни. Вот строгая формулировка моего закона:
Гипотеза биологического масштабирования. Если мы копируем живое существо, так что одно квантовое состояние копируется другим квантовым состоянием и гамильтониан копии равен
НC = λUHU-1, (55)
где Н — гамильтониан существа, U — унитарный оператор, а λ — положительный масштабный фактор; и если окружающая среда копируется таким же образом, так что температуры окружающей среды оригинала и копии равняются соответственно Т и λT, то копия живет и является субъективно идентичной оригиналу, с той лишь разницей, что скорость всех ее жизненных функций снижается в соответствии с тем же фактором λ.
Достоверность этой гипотезы обеспечивает структура уравнения Шредингера, где время и энергия действуют как взаимосвязанные переменные. В настоящее время это чисто теоретическая гипотеза, никакая экспериментальная ее проверка невозможна. Дабы избежать неверного понимания, подчеркну, что закон масштабирования неприменим к изменениям уровня обмена веществ в данном организме как функции от температуры. Например, когда змея или ящерица меняют температуру тела, скорость их обмена веществ зависит от Т скорее экспоненциально, чем линейно. Линейный закон масштабирования применим к набору копий змеи, каждая из которых приспособлена к определенной температуре. К отдельной змее с изменяющимся Т он отношения не имеет.
Итак, с этого момента я считаю гипотезу масштабирования валидной и намерен рассмотреть ее последствия для возможностей жизни. Первое следствие — это то, что субъективное время, переживаемое живым существом, не является физическим временем t, но определяется по формуле:
u(t) = f ∫0t θ(f') dt', (56)
где θ(t) — температура существа, a f = (300 deg sec)-1 — фактор шкалы, позволяющей сделать и безразмерным. Я называю и «субъективным временем». Второе следствие временного закона — то, что любое существо характеризуется числом Q, обозначающим скорость производимой им энтропии в единицу субъективного времени. Если энтропия измеряется в единицах информации или битах и если и измеряется в «моментах сознания», то Q — число, обозначающее объем информации, достаточный для того, чтобы поддержать жизнь существа на мгновение, достаточное для мысли: «Cogito, ergo sum» [я мыслю — следовательно, существую]. Я называю Q сложностью живого существа. Например, при температуре 300 К человек расходует мощность около 200 ватт, причем каждый момент сознания продолжается около секунды. Таким образом, Q человека равно
Q = 1023 бит. (57)
Таким образом, Q — это единица сложности молекулярных структур, задействованных в единичном акте человеческого сознания. Для человеческого рода в целом
Q = 1033 бит (58)
— число, сообщающее нам, какое множество материальных ресурсов требуется для поддержания жизни разумного сообщества.
Существо или сообщество существ с данным Q и данной температурой θ будет тратить энергию со скоростью:
m = kfQθ2. (59)
Здесь m — скорость обмена веществ, измеряемая в эргах в секунду, k — константа Больцмана, a f — коэффициент, использовавшийся в (56). Важно отметить, что m пропорционально квадрату θ, причем один фактор θ происходит из взаимоотношений между энергией и энтропией, а второй фактор θ — из принятой зависимости скорости жизненных процессов от температуры.
Я предполагаю, что жизнь свободна выбирать себе температуру θ(t) таким образом, чтобы максимально увеличить свои шансы на выживание. Существуют два физических ограничения на θ(t). Первое — θ(t) всегда должна быть выше температуры универсальной фоновой радиации, являющейся самой низкой из достижимых температур. Иначе говоря,
θ(t) >aR-1, а = 3∙1028 deg cm, (60)
где R — радиус вселенной, изменяющийся в зависимости от t, согласно (7) и (8). В настоящее время условие (60) удовлетворяется со 100–кратным запасом. Второе ограничение θ(t) — это то, что физический механизм может существовать, лишь выделяя в пространство огромное количество лишнего тепла, возникающего в результате обмена веществ. Чтобы сформулировать второе ограничение количественно, примем, что лишнее тепло удаляется из организма посредством излучения и что единственная значимая форма излучения — электромагнитное. Тогда мы получаем абсолютный верхний предел
I(θ)<2γ(Ne2/mh2c3) (kθ)3 (61)
мощности, которая может испускаться материальным источником, содержащим в себе N электронов, при температуре Θ. Здесь
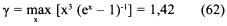
— высота максимума спектра планковского излучения. Поскольку формулы (61) я в учебниках не нашел, приведу краткое доказательство, используя статью Бета и Сэлпитера (Bethe and Salpeter, 1957). Формула мощности, выделяемой излучением электрического диполя, следующая:
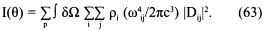
Здесь p — поляризационный вектор фотона, испускаемого внутри угла dΩ, i — начальное, a j — конечное состояния излучателя,
ρi = Z-1exp (-Еi/kθ) (64)
— вероятность, что излучатель изначально находится в состоянии i,
ωij=h-1(Ei-Ej) (65)
— частота фотона, a Dij — матричный элемент дипольного момента излучателя между состояниями i и j. Сумма (63) определяется только между парами состояний (i, j), причем
Еi >Еj. (66)
Теперь у нас есть точное правило суммирования дипольных моментов:
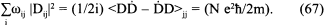
Однако использовать формулу (67) для нахождения связи с (63) следует с осторожностью, поскольку некоторые члены в (67) отрицательные. Здесь может помочь следующая хитрость. В каждом члене (63) ω^, согласно (66), положительно; таким образом, (62) дает нам:
ρiωij3< γρί (kθ/h)3(exp(hωij / kθ) - 1) = γ (ρj - ρi) (kθ/h)\ (68)
Таким образом, из (63) следует:
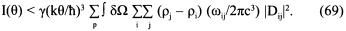
Теперь индексы суммирования (i, j) можно поменять в той части формулы (69), которая содержит ρi. Получаем результат:
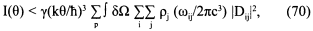
где суммирование теперь проводится по всем (i, j) независимо от того, выполняется (66) или нет. Правило суммирования (67) можно затем использовать в (70) и получить результат (61).
Это доказательство (61) предполагает, что все частицы, кроме электронов, обладают такой большой массой, что при расчетах генерируемого излучения ими можно пренебречь. Оно предполагает также, что можно пренебречь магнитным дипольным и многополюсным излучением. Интересно было бы узнать, можно ли доказать (61), не используя дипольное приближение (63).
С первого взгляда может показаться странным, что правая сторона (61) пропорциональна θ3, а не θ4, поскольку стандартная формула Стефана–Больцмана для мощности, испускаемой черным телом, пропорциональна θ4. Однако в этом случае формула Стефана–Больцмана неприменима, поскольку она требует от излучателя оптической плотности. Максимум испускаемой мощности, заданный (61), может быть достигнут, только если излучатель оптически прозрачен.
Сделав это небольшое отступление в область физики, вернемся к биологии. Второе ограничение на температуру θ связано с тем, что скорость траты энергии (59) не должна превышать мощность (61), способную выделяться в пространство. Это ограничение накладывает на нас нижний температурный предел:
kθ >(Q/N)ε = (Q/N) 10 28 erg, (71)ε = (137/2γ)(hf/k)mc2, (72)θ >(Q/N) (ε/κ) = (Q/N) 10–12 deg. (73)
Соотношение (Q/N) между сложностью сообщества и числом электронов, находящихся в его распоряжении, не может быть произвольно мало. Для современного человечества, с Q, заданным (58), и
N= 1042 (74)
(количество электронов в биосфере земли), соотношение равно 10–9. С течением развития и усложнения общества это соотношение скорее увеличивается, чем уменьшается. Таким образом, (73) и (59) предполагают более низкий предел скорости излучения энергии для общества заданной сложности. Поскольку общий объем энергии, доступной сообществу, конечен, конечно и время его существования. Мы пришли к печальному заключению, что одного замедления обмена веществ, описанного в моей гипотезе биологического времени, недостаточно для того, чтобы сообщество жило вечно.
К счастью, у жизни есть и другая стратегия, дающая надежду избегнуть печальной участи, а именно впадение в спячку. Обмен веществ может совершаться с перерывами; при этом излучение лишней энергии может не прерываться и в периоды спячки. В активной фазе жизнь может находиться в термальном контакте с излучателем при температуре θ. В спячке излучатель может по–прежнему сохранять температуру θ, но сама жизнь — поддерживать гораздо более низкую температуру, так что обмен веществ, в сущности, остановится.
Предположим, что сообщество проводит часть g(t) своего времени в активной фазе, а часть [1—g(t)] в спячке. Циклы активности и спячки должны быть достаточно коротки, чтобы значения g(t) и θ(t) не испытывали значительных колебаний в течение одного цикла. Формулы (56) и (59) больше не работают. Вместо них субъективное время определяется формулой
u(t) = f∫0t g(t') θ(t') dt', (74)
и средняя скорость излучения энергии равняется
m = kfQgθ2. (75)
Ограничение (71) заменяется
θ(t) >(Q/N) (ε/k) g(t). (76)
Жизнь выделяет мощность в соответствии с ограничением (61), увеличивая продолжительность жизненных циклов пропорционально снижению температуры.
Приведем пример возможной стратегии долгоживущего сообщества. Мы можем удовлетворить условиям (60) и (76) в широких пределах, если примем
g(t) = (θ(t)/θ0) = (t/t0)-α, (77)
где θ0 и t0 — нынешняя температура жизни и нынешний возраст вселенной. Экспонента а должна лежать в пределах
1/3< α< 1/2. (78)
Для большей определенности примем
α = 3/8. (79)
Тогда, согласно (74), получаем субъективное время
u(t) = A(t/to)1/4, (80)
где
A = 4fθ0t0= 1018 (81)
— текущий возраст вселенной, измеряемый в моментах сознания. Средняя скорость излучения энергии, согласно (75), равняется
m(t) = kfQθ02 (t/t0)-9/8. (82)
Общее количество энергии, переработанной от момента t0 до бесконечности, равняется
∫t0∞ m(t) dt = BQ, (83)B = 2Akθ0 = 6∙104 erg. (84)
Этот пример показывает, что с помощью стратегии спячки жизнь может достигнуть одновременно двух своих главных целей. Во–первых, согласно (80), субъективное время бесконечно; хотя с расширением вселенной биологические часы замедляются и начинают работать с перерывами, субъективное время длится вечно. Во–вторых, согласно (83), общее количество энергии, требуемой для бесконечного выживания, конечно. Условий (78) достаточно, чтобы сделать интеграл (83) сходящимся, а интеграл (84) расходящимся при t —> ∞.
Согласно (83) и (84), запас свободной энергии, необходимой для бесконечного выживания сообщества со сложностью (58) современного человечества, начиная с настоящего времени и до бесконечности, составляет порядка
BQ = 6∙1037 erg (85)
— примерно столько же энергии, сколько излучает солнце за восемь часов. Энергетических ресурсов галактики хватит, чтобы вечно поддерживать сообщество со сложностью в 1024 раз больше, чем наше.
Эти заключения валидны для открытой космологии. Интересно отметить, что в закрытой космологии ситуация совсем другая. Если жизнь попытается выжить в течение бесконечного субъективного времени в закрытой космологии, ускоряя свой обмен веществ по мере сжатия вселенной и возрастания температуры фонового излучения, отношения (56) и (59) сохранятся, но физическое время t будет иметь конечную продолжительность (5). Если
τ = 2πТ0 - t, (86)
то температура фонового излучения —
θR(t) = a(R(t))-1 (87)
пропорциональна τ -2/3 при τ—>0, благодаря (2) и (3). Если температура θ(t) жизни остается близкой к θR при τ—>0, то интеграл (56) конечен, а интеграл (59) бесконечен. У нас имеется бесконечная необходимость в энергии для достижения конечного субъективного срока существования. Если θ(t) стремится к бесконечности медленнее, чем θR, общая протяженность субъективного времени остается конечной. Если θ(t) стремится к бесконечности быстрее, чем θR, энергетические требования для обмена веществ остаются бесконечными. Биологические часы никогда не ускоряют свой ход настолько, чтобы втиснуть бесконечное субъективное время в конечную вселенную.
С чувством облегчения я возвращаюсь в бесконечный простор открытой вселенной. Нет нужды подчеркивать частичный и предварительный характер заключений, представленных мною в этой лекции. Я всего лишь очень грубо очертил некоторые из физических проблем, с которыми может столкнуться жизнь в попытке выжить в холодной вселенной. Я даже не пытался справиться со всем множеством вопросов, которые возникают, едва пытаешься представить в деталях архитектуру жизненной формы, приспособленной к сверхнизким температурам. Будут ли в низкотемпературных системах существовать функциональные эквиваленты мышц, нервов, рук, голоса, глаз, ушей, мозга и памяти? На эти вопросы у меня нет ответов.
Впрочем, о памяти можно кое-что сказать, не вдаваясь в детальное обсуждение проблем архитектуры, поскольку память — понятие абстрактное. Способность к запоминанию можно описать количественно, в виде определенного числа битов информации. Мне хотелось бы, чтобы наши потомки были снабжены не только субъективно бесконечно долгой жизнью, но и безмерно возросшей вместительностью памяти. Быть бессмертным, но с конечной памятью — что в этом хорошего? Едва ли есть смысл в бессмертии, если придется стирать воспоминания о своем прошлом, чтобы освободить место для нового опыта. Существуют две формы памяти, известные физикам: цифровая и аналоговая. Все современные компьютерные технологии построены на цифровой памяти. Но цифровая память принципиально ограничена числом атомов, используемых для ее постройки. Общество, чьи материальные ресурсы конечны, никогда не сможет создать цифровую память, не имеющую предельной вместимости. Следовательно, цифровая память не подходит для нужд жизненной формы, рассчитывающей на вечную жизнь.
К счастью, у аналоговой памяти, основанной на фиксированном числе компонентов в расширяющейся вселенной, таких ограничений нет. Например, такое физическое явление, как угол между двумя звездами в небесах, может быть использовано как единица аналоговой памяти. Вместимость этой единицы памяти равна числу значимых двоичных чисел, которыми может быть измерен этот угол. По мере того как вселенная расширяется и звезды редеют, число значимых чисел в угле увеличивается логарифмически. Значения атомных частот и уровней энергии в принципе могут быть измерены множеством значимых цифр, пропорциональным (log t). Следовательно, бессмертной цивилизации нужно будет найти способ закодировать свои архивы в аналоговой памяти, вместимость которой возрастает как (log t). Такая память наложит жесткие ограничения на получение вечных новых знаний, но по крайней мере не преградит им путь вовсе.
Лекция IV. Коммуникация
В этой последней лекции я разберу проблему коммуникации между двумя сообществами, разделенными значительным расстоянием в открытой вселенной, описываемой формулой (6). Я предполагаю, что они общаются друг с другом с помощью электромагнитных сигналов. Без потери общности можно считать, что сообщество А, двигаясь по мировой линии χ=0, передает сигнал, а сообщество В, двигаясь по линии с координатами χ=η, его получает. Сигнал, переданный А во временной координате ψ = ξ, В получает во временной координате ψ = ξ + η. Если частота передачи — со, то частота приема будет иметь красное смещение по формуле

RA = cT0 (coshξ — 1), (89)RB = cT0 (cosh(ξ + η) — 1). (90)
Ширина полосы В и ширина полосы В' будут связаны тем же фактором (1 + z). Точное расстояние между А и В на момент приема сигнала — dL = RBη. Однако площадь сферы χ = η в то же самое время равна 4πdT2, с
dT = RBsinhη. (91)
Если А передает F фотонов в стерадиан в направлении В, число фотонов, принятых В, будет составлять
F' = (F∑' / d2T), (92)
где ∑' — эффективное сечение приемника.
Теперь сечение приемника, поглощающего фотон с частотой ω', задано формулой, подобной формуле (63) из предыдущей лекции:
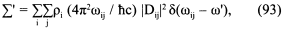
где Dij — снова дипольный матричный элемент между состояниями i и j. Проинтегрировав все это относительно всех ω', мы получаем в точности левую половину правила суммы (67). Вклад от отрицательного ω' представляет собой наведенное излучение фотонов получателем. Я предполагаю, что получатель не связан с поступающими фотонами, и, следовательно, наведенным излучением можно пренебречь. Таким образом, у нас получается
∫0∞ ∑'dω' = Ν' (2π2е2/mc), (94)
где Ν' — число электронов приемника. Если приемник настроен на частоту ω' с ширингой полосы В', (94) дает нам
Σ'Β' ≤ Ν' S0, (95)S0 = (2π2e2/mc) = 0,167 cm2 sec-1. (96)
Чтобы избежать смешивания единиц, я измеряю как ω', так и В' не в герцах, а в радианах в секунду. Полагаю, высокоразвитая цивилизация сможет создать приемник, для которого соотношение (95) выполняется со знаком равенства. Тогда (92) примет следующий вид:
F' = (FN' S0/d2TB'). (97)
Я предполагаю, что передатчик содержит N электронов, способных создать направленное излучение с углом распространения, составляющим порядка N-1/2. Если передатчик представляет собой луч, состоящий из N диполей с оптимальными фазами, число фотонов на стерадиан в луче составляет
F = (3N/8π) (E/hω), (98)
где Е — общий объем переданной энергии. Число полученных фотонов равняется
F' — (3NN1 ES0 / 8πhωd2TB'). (99)
Из (99) мы сразу видим, что для увеличения числа передаваемых фотонов необходимы низкие частоты и узкие полосы. Однако мы заинтересованы в передаче не фотонов, а информации. Чтобы эффективно извлекать информацию из заданного числа фотонов, нам придется использовать ширину полосы, равную скорости детектирования:
B' = (F'/τB), B = (F'/τA), (100)
где τв — продолжительность приема, а τА — продолжительность передачи. При этой ширине полосы F' представляет как число фотонов, так и число принятых битов информации. Удобно выражать τв и τА как долю радиуса вселенной во время передачи и приема информации:
τA = (δRA/c), τB = (δRB/c). (101)
Условие
δ ≤ 1 (102)
устанавливает нижний предел ширины полосы В. Предположим также для простоты, что частота со сделана такой низкой, как только возможно, в соответствии с шириной полосы В, а именно:
ω = В, ω' = В'. (103)
Тогда (99), (100) и (101) дают
F' = {NN'52E / [(1+z) (sinh2η)Ec]}1/3, (104)
где, согласно (96),
Ес = (8πhc2 / 3S0) = (4/3π)137mc2 = 3∙105 erg. (105)
Из (104) мы видим, что количество информации, которую можно передать от А к В через заданный объем энергии, со временем, по мере расширения вселенной и отдаления А и В друг от друга, не уменьшается. Увеличение расстояния компенсируется снижением энергетической стоимости каждого фотона и увеличением угла приема при уменьшении длины волны.
Полученный сигнал задается формулой (104). Теперь нам необходимо сравнить его с полученным шумом. Фоновый шум во вселенной на частоте со можно описать эквивалентной температурой шума TN, так что число фотонов на единицу волны на стерадиан на квадратный сантиметр в секунду описывается формулой Релея–Джинса:
I(ω) = (kTNω / 4π3hc2). (106)
Эта формула — просто определение TN, которое в целом представляет собой функцию со и t. Я не предполагаю, что шум обладает планковским спектром на всех частотах. Лишь часть шума принадлежит изначальной фоновой радиации, обладающей планковским спектром при температуре θR. Изначальная шумовая температура θR изменяется обратно пропорционально радиусу вселенной:
(kθRR/hc) = Λ= 1029, (107)
где R задано формулой (8). Я полагаю, что спектр шума в целом по мере расширения вселенной изменяется в том же соотношении с радиусом и таким образом:
(TN/θR) = f(x), х = (hω/kθR), (108)
где f есть универсальная функция от х. Если х близко к единице, то в шуме преобладает реликтовое излучение и f(x) имеет планковскую форму
f(x) = fP(x) = х (ех — 1)-1, х ~ 1. (109)
Однако возможны значительные отклонения от (109) как при большом х (результате красного смещения звездного света), так и при маленьком х (результате нетермальных радиоизлучений). Не углубляясь в детали, скажем просто, что f(x) в целом является уменьшающейся функцией х и быстро стремится к нулю по мере того, как х —> ∞.
Общая энергетическая плотность радиации во вселенной составляет
(4π/c) ∫I(ω) hωdω = (kθR)4I / (π2h3c3), (110)
где
I = ∫0∞f(x)x2dx. (1ll)
Интеграл I должен сходиться как при высоких, так и при низких частотах. Следовательно, мы можем найти такое числовое ограничение b, что
x3f(x)<b (112)
для всех х. В сущности, (112), вероятно, выполняется при b = 10, если мы будем избегать некоторых определенных частот, например водородной линии 1420 Мгц.
Число шумовых фотонов, полученных в течение времени tB приемником с шириной полосы В' и сечением составляет
FN = 4π∫'B'τBI(ω'). (113)
Подставляя значения из (95), (96), (100), (103) и (108) в (113), получаем:
FN = (2r0/λB)fN'F', (114)
где
r0 = (e2/mc2) = 3∙10–13cm, (115)
а
λB = (hc / kθ'R) = Λ-1RB (116)
— длина волны фонового реликтового излучения во время приема сообщения. Если F' — сигнал, то отношение сигнала к шуму равняется
RSN = (λB / 2fN'r0). (117)
В этой формуле f — отношение шума и температуры, заданное (108), N' — число электронов приемника, а ρ0, λB заданы (115) и (116). Отметим, что в вычислении (117) мы не даем приемнику возможности выбора угла, поскольку сечение заданное (95), не зависит от направления.
Теперь подведем итоги нашего анализа. У нас имеются передатчик и приемник на мировых линиях А и В, передающие и принимающие сигналы во время tA = Т0 (sinhξ — ξ), tB = Т0 (sinh(ξ + η) — (ξ + η)). (118)
Согласно (89) и (101),
τA = δ(dtA/dξ), τB = δ(dtB/dξ). (119)
Для удобства будем считать, что передатчик постоянно направлен на приемник и передает сообщения с определенным циклом 8, который может изменяться в зависимости от Когда 5 = 1, передатчик все время включен. Число F' фотонов, принимаемых во время τв, может рассматриваться как количество битов в отношении к переменной ξ. В сущности, F'dξ — это число битов, получаемых в интервале dξ. Работать с переменной ξ полезно, поскольку она поддерживает постоянное различие л между А и В.
Из (100), (101), (103), (107) и (108) мы выводим простую формулу количества битов:
F = Λхδ. (120)
Энергия Е, переданная во время τА, может также рассматриваться как скорость передачи энергии в единицу интервала Из (104) и (120) мы выводим
Е = (Λ3 / NN') (1 + z) (sinh2η)x3δEc. (121)
Мы все еще можем свободно выбирать параметры х [определяя частоту со согласно (108)] и 5, оба из которых могут изменяться в зависимости от Единственные ограничения — (102) и сигнально–шумовое условие
RSN≥10, (122)
где соотношение сигнала и шума вычисляется согласно (117). Если мы предположим, что (112) верно при b = 10, (122) будет обеспечивать, что
х >(G/r)1/3, (123)
где
G = (200r0 / λp) N' (1+z)-1 = 10–9N' (1+z)-1, (124)r = (RA / Rp) = (cosh ξ – 1) / (cosh ξp – 1). (125)
Здесь λp, Rp и ξp — текущие значения длины волн фоновой радиации, радиуса вселенной и временной координаты ψ Стоит отметить, что сигнально–шумовое условие (123) может быть трудно для соблюдения поначалу, пока r мало, но с течением времени, по мере того как во вселенной становится все тише, его становится все легче выполнять. Чтобы избежать чрезмерной траты энергии на ранних стадиях, вначале мы выбираем маленький цикл 5 и постепенно увеличиваем его, пока он не достигает единицы. Все условия выполняются, если мы выбираем
х = max [(G / r)1/3, ξ-1/2], (126)δ = min [(r / G)ξ-3/2, 1], (127)
так что
х3δ = ξ-3/2 (128)
для всех Переход между двумя уровнями в (126) и (127) происходит при
ξ = ξT~logG, (129)
поскольку ξ логарифмически возрастает вместе с r согласно (125). При таком выборе х и 8 (120) и (121) дают следующее:
F' = Λmin [(r / G)2/3ξ-3/2, (130)Е = (Λ3 / NN') (1+z) (sinh2η) Еcξ-3/2. (131)
Теперь рассмотрим общее число битов, полученных В вплоть до некоей эпохи ξ в отдаленном будущем. Согласно (130), их число равно приблизительно
FT = ∫χ F'dξ = 2Λξ1/2 (132)
и беспредельно возрастает по мере возрастания С другой стороны, общее количество энергии, излученной передатчиком на протяжении всего будущего, конечно:
Ет = ∑ξ, Edξ = 2(Λ3 / NN') (еη sinh2η)ξp-1/2Ec. (133)
В (133) я заменил красное смещение (1 + z) его асимптотическим значением еη при ξ —> оо. В результате я получил такое же оптимистическое заключение относительно возможностей коммуникации, как и на предыдущей лекции — относительно возможностей выживания. Оказывается, в принципе возможно вечно поддерживать коммуникацию с отдаленным сообществом в расширяющейся вселенной, используя конечный объем энергии.
Интересно прикинуть хотя бы грубое численное значение величин FT и ЕТ. Согласно (107), кумулятивное количество битов в каждом коммуникационном канале одинаково, порядка
FT = 1029ξ1/2, (134)
— количество информации, вполне достаточное для передачи истории сложной цивилизации. Чтобы оценить ЕТ, я предполагаю, что как передатчик, так и приемник содержат в себе 1 кг электронов, так что
N = N' = 1030. (135)
Затем (133) вместе с (105) дает
Ет = 1023 (eηsinh2η) erg. (136)
Это порядка 109 ватт∙лет — и по астрономическим стандартам очень малое количество энергии. Общество, имеющее доступ к энергетическим ресурсам звезды солнечного типа (около 1036 W лет), с легкостью обеспечит себя энергией для создания постоянных коммуникационных каналов с 1022 звездами, лежащими в пределах сферы η< 1. Иначе говоря, все сообщества внутри красного смещения
z = e – 1 = 1.718 (137)
смогут поддерживать постоянную связь между собой. С другой стороны, прямая коммуникация между двумя сообществами, находящимися на значительном расстоянии друг от друга, может оказаться непомерно дорогой. Из-за быстрого экпоненциального роста Ет с η, верхний предел уровня возможной прямой коммуникации лежит в районе η = 10.
На расстояния, большие η = 10, легко передавать информацию без чрезмерных затрат энергии, если сообщества, расположенные по маршруту передачи сигнала, будут работать как трансляционные станции, принимая, усиливая и ретранслируя сигнал. В этом случае мы сможем передавать сообщения на сколь угодно большие расстояния во вселенной. В конечном счете каждое сообщество во вселенной сможет поддерживать контакт со всеми остальными.
Как я отмечал в первой лекции [см. равенство (11)], число галактик, лежащих в сфере η< ψ, возрастает подобно e2ψ, когда ψ велико. Так что, если мы попытаемся установить связь между отдаленными сообществами, перед нами встанет проблема жесткого отбора сообществ. Вдали от нас слишком много галактик. К каким из них прислушиваться? В какие отправлять сообщения? Чем более совершенны будут наши технические средства коммуникации, тем труднее нам будет решать, от каких коммуникаций отказываться.
В заключение хотелось бы подчеркнуть, что я не пытаюсь доказать свое утверждение — то, что возможна передача бесконечного количества информации средствами ограниченного объема энергии. Чтобы это доказать, мне следовало бы сконструировать передатчик и приемник и показать, как они работают. Я никогда даже не пытался представить себе конструкцию такой коммуникационной системы. Все, что я хотел, — показать, что система, работающая согласно моим спецификациям, не противоречит известным нам законам физики и теории информации.
Вселенная, которую я несколькими штрихами обрисовал в этих лекциях, очень отличается от той, которую имел в виду Стивен Уэйнберг, говоря: «Чем лучше мы понимаем вселенную, тем бессмысленнее она нам представляется». В моей вселенной нет пределов богатству и сложности бытия; в ней жизнь продолжается вечно, и живые существа обмениваются знаниями с себе подобными через невообразимые пропасти пространства и времени. Какая вселенная ближе к истине — Уэйнберга или моя? Что ж, когда-нибудь, быть может довольно скоро, мы это узнаем.
Верны или нет детали моих вычислений — думаю, мне удалось показать, что существует достойная научная основа для принятия всерьез возможности, что жизни и разуму удастся приспособить нашу вселенную к своим целям. Как написал пятьдесят лет назад биолог Холдейн (1924), «человеческий разум хрупок, и не всегда он соответствует величию своих притязаний. Но и тогда:
Хоть в шутку он кланяется богам,
Я знаю, он спорит с ними, пока
Не сгинет в последней тьме.
Литература
1. Alpher, R. A., R. C. Herman, and G. Gamow, 1948, Phys. Rev. 74, 1198.
2. Barrow, J. D., and F. J. Tipler, 1978, "Eternity Is Unstable", Nature (Lond.) 276, 453.
3. Bethe, H. A., and E. E. Salpeter, 1957, "Quantum Mechanics of One- and Two-Electron Systems" in Handb. Phys. 35, 334–348.
4. Capek, K., 1923, R. U.R., translated by Paul Selver (Doubleday, Garden City, N. Y.).
5. Davies, P. C.W., 1973, Mon. Not. Roy. Astron. Soc. 161, 1.
6. Dyson, F. J., 1972, Aspects of Quantum Theory, edited by A. Salam and E. P. Wigner (Cambridge University, Cambridge, England), Chap. 13.
7. Dyson, F. J., 1978, "Variation of Constants", in Current Trends in the Theory of Fields, edited by J. E. Lannutti and P. K. Williams (American Institute of Physics, New York), pp. 163–167.
8. Feinberg, G., M. Goldhaber and G. Steigman, 1978, Multiplicative Baryon Number Conservation and the Oscillation of Hydrogen into Antihydrogen, Columbia University Preprint CU-TP-117.
9. Godel, K.9 1931, Monatsch. Math. Phys. 38, 173.
10. Gott, J. R., III, J. E. Gunn, D. N. Schramm, and B. M. Tinsley 1974, Astrophys. J. 194, 543.
11. Gott, J. R., III, J. E. Gunn, D. N. Schramm, and B. M. Tinsley 1977, Sci. Am. 234, 62 (March, 1976).
12. Haldane, J. B.S., 1924, Daedalus, or Science and the Future (Kegan Paul, London).
13. Harrison, J. B.S., K. S.Thorne, M. Wakano, and J. A. Wheeler, 1965, Gravitation Theory and Gravitational Collapse (University of Chicago, Chicago), Chap. 11.
14. Hawking, S. W., 1975, Commun. Math. Phys. 43, 199.
15. Hoyle, F., 1957, The Black Cloud (Harper, New York).
16. Islam, J. N., 1977, QJ. R. Astron. Soc. 18, 3.
17. Islam, J. N., 1979, Sky Telesc, 57, 13.
18. Kropp, W. P., and F. Reines, 1965, Phys. Rev. 137, 740.
19. Maurette, M., 1976, Annu. Rev. Nucl. Sci. 26, 319.
20. Monod, J., 1971, Chance and Necessity, translated by A. Wainhouse (Knopf, New York) [Le Hazard et la Necessite, 1970 (Editions du Seuil, Paris)].
21. Nagel, E., and J. R. Newman, 1956, Sci. Am. 194, 71 (June, 1956).
22. Nanopoulos, D. V., 1978, Protons are not Forever, Harvard Preprint HUTP-78/A062.
23. Pati, J. C., 1979, Grand Unification and Proton Stability, University of Maryland Preprint No.79–171.
24. Penzias, A. A., and R. W. Wilson, 1965, Astrophys. J. 142, 419.
25. Rees, M. J., 1969, Observatory 89, 193.
26. Shlyakhter, A. L., 1976, Nature (Lond.) 264, 340.
27. Turner, M. S., and D. N. Schramm, 1979, The Origin of Baryons in the Universe and the Astrophysical Implications, Enrico Fermi Institute Preprint No. 79–10.
28. Weinberg, S., 1972, Gravitation and Cosmology (Wiley, New York), Chap. 15.
29. Weinberg, S., 1977, The First Three Minutes (Basic, New York).
30. Wright, Т., 1750, An Original Theory or New Hypothesis of the Universe, facsimile reprint with introduction by M. A. Hoskin, 1971 (MacDonald, London, and American Elsevier, New York).
31. Zeldovich, Y. B., 1977, Sov. Phys. — JETP45, 9.
Назад: 7. Экзотические генетические материалы и распространенность жизни во Вселенной
Дальше: 9. Жизнь во Вселенной Цифровая или аналоговая?

