Ученые любят описывать изучаемые объекты при помощи чисел, так же как сделали мы с показаниями ящиков Белла. Это помогает сосредоточить внимание на главном и не путаться в длинных предложениях вроде «Алиса наклонила джойстик влево и получила результат 0». Математический аппарат также помогает выполнять сложение и умножение, и мы увидим, что можно уместить понятие нелокальности в очень простом уравнении.

Сначала займемся Алисой. Пусть переменная х обозначает ее выбор, а переменная a – результат. К примеру, х = 0 будет означать, что Алиса выбрала наклонить джойстик влево, а х = 1 будет означать, что она наклонила его направо. Точно так же обозначим переменные для Боба: y будет обозначать его выбор, а b – результат. При таких обозначениях следующая небольшая таблица описывает случаи, в которых, согласно правилам, Алиса и Боб получают очко.

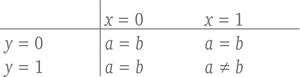
Оказывается, простые арифметические действия помогут нам свести всю игру Белла, в которой у Алисы и Боба имеется по ящику, которые далеко разнесены друг от друга, чтобы избежать какой-либо возможности копирования, где каждый из них делает свободный выбор и записывает результат, в одно элегантное уравнение:

то есть сумма а и b равна произведению х и у.

В самом деле, произведение х × у всегда равно 0, кроме случая, когда х = у = 1. Следовательно, говорит нам уравнение, сумма a + b всегда равна 0, кроме случая, когда х = у = 1.

Сначала рассмотрим случай, при котором x = y = 1. Сумма a + b при этом равна 1, а так как мы договорились, что переменные a и b могут принимать только значения 0 и 1, то уравнение a + b = 1 имеет два решения: или a = 0 и b = 1, или a = 1 и b = 0. Следовательно, если a + b=1, то a ≠ b. В этом случае в соответствии с правилами игры участники получают очко.

Теперь рассмотрим три оставшихся случая: (x, y) = (0, 0), (0,1) или (1,0). Во всех трех случаях произведение x × y равно 0, поэтому мы можем упростить уравнение до a + b = 0. Первое возможное решение – a = b = 0. Второе решение: это a = b = 1. Второе решение на первый взгляд кажется странным, потому что сумма 1 + 1 обычно равна 2. Но, так как мы считаем битами, нулями и единицами, результат также может быть представлен только как 0 или 1. В нашем случае 2 = 0 (математики сказали бы о сравнении по модулю 2). Следовательно, уравнение a + b = 0 эквивалентно a = b.

Таким образом, одно красивое уравнение a + b = x × y весьма лаконично описывает игру Белла. Каждый раз, когда уравнение удовлетворяется, Алиса и Боб получают очко. Теперь вы убедились, что революционные идеи квантового мира могут выражаться довольно простой математикой.

Это уравнение выражает явление нелокальности. Ведь для того, чтобы систематически побеждать в игре Белла, ящики должны сами вычислять произведение x × y. Но если выбор x доступен только на приборе Алисы, а выбор y – только на приборе Боба, то такой расчет невозможно выполнить локально. В лучшем случае они могут поставить на x × y = 0, и они будут правы в трех случаях из четырех, так что счет составит 3. Любой счет больше 3 требует «нелокального» вычисления x × y, потому что оба множителя существуют на огромном расстоянии друг от друга.