Если вы раздадите математический тест десяти тысячам случайно выбранных людей, вы обнаружите, что их оценки попадают в некую область вокруг среднего значения. Разброс полученных данных будет соответствовать так называемому нормальному статистическому распределению, которое визуально выражается известной кривой нормального распределения. Ответы, заметно отличающиеся от среднего значения, очень маловероятны, или, как говорят математики, «экспоненциально» маловероятны. Любая кривая нормального статистического распределения имеет «стандартное отклонение», характеризующееся широтой разброса ответов, которую можно оценить с помощью статистических расчетов. Если тест оценивается по 100-балльной шкале, то наиболее вероятной оценкой может быть 70 баллов при стандартном отклонении, возможно, в 7 или 8 баллов. По определению, вы не найдете ни одной оценки, отстоящей от среднего значения более чем на величину некоторого стандартного отклонения в ту или иную сторону (рис. 2).

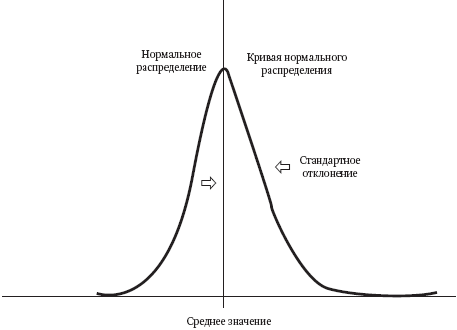
Рис. 2. Гауссово распределение, также известное как колоколообразная кривая нормального распределения. Визуально отражает статистические данные о результатах тестирования, росте, весе и многих других показателях. Это обычное распределение любого параметра, отражающего совместные действия многих неопределенных независимых факторов.

Но что произойдет, если участники тестирования будут отобраны не случайным образом? Если участники тестирования – студенты и половина из них изучает математику, а другая – английскую литературу, то их оценки распределятся на две группы, сосредоточенные вокруг разных средних значений, при этом студенты-математики будут демонстрировать лучшие результаты. В этом случае вам придется построить кривую с двумя выпуклостями вместо одной, что будет свидетельствовать о наличии двух различных типов участников, входящих в группу испытуемых. Если же далеко справа на графике вы заметите небольшую третью выпуклость, отражающую наличие очень высоких оценок, это может свидетельствовать о том, что в группу испытуемых затесалось несколько профессиональных математиков. Другой тест – написать небольшое эссе на тему соперничества Уильяма Шекспира и Кристофера Марло – позволит выявить имеющиеся в группе различия в совершенно ином измерении знаний и способностей.

В этом смысле статистический анализ является своего рода математическим ультразвуком, способным выявить скрытую информацию. Какая же информация о землетрясениях скрыта от нас? При построении кривой распределения магнитуды землетрясений можно ожидать, что на графике будут заметны сразу несколько выпуклостей. Одни землетрясения происходят глубоко под землей, а другие ближе к поверхности. Одни фиксируются в регионах, где преобладает твердая и хрупкая горная порода, другие – там, где она более пластична. Различные виды землетрясений – и в их числе землетрясения, вызываемые мегасдвигами, – по идее должны проявиться на графике в виде нескольких выпуклостей, каждая из которых будет объединять эти явления на основании некоторых типичных параметров.

Как ни странно, но вид графика, полученного учеными, изучавшими землетрясения, очень отличался от ожидаемого. В 1950 году сейсмологи Бено Гутенберг и Чарльз Рихтер из Калифорнийского технологического института провели обширную перепись землетрясений, наблюдавшихся по всему миру на протяжении многих лет. В результате они вообще не обнаружили никаких выпуклостей. Оказывается, землетрясения не группируются по своему типу, но подчиняются очень простому правилу: сильные землетрясения происходят стабильно реже, чем слабые.Такую статистическую картину называют «степенно́й зависимостью», поскольку вероятность события напрямую зависит в данном случае от степени его мощности. В частности, если вы оцените мощность землетрясений по количеству выделяемой энергии, то обнаружите, что количество землетрясений обратно пропорционально возведенному в квадрат количеству энергии. Землетрясения удвоенной силы случаются в четыре раза (два в квадрате) реже. Это справедливо для любого типа данного природного явления, от легкой земной дрожи до мощнейших землетрясений, вызванных мегасдвигами.

Таким образом, землетрясения, несмотря на нашу полную неспособность к их предсказанию, подчиняются удивительному по своей простоте статистическому порядку. В данном случае кривая нормального распределения не содержит даже намека на отражение различий по видам или классам землетрясений, как это было в описанном выше примере тестирования студентов, имеющих различные уровни подготовки. Нет ничего, что указывало бы на существование какого-либо качественного различия между слабыми и сильными землетрясениями.

Лондонцы часто вспоминают шутку о городских автобусах: вы ждете, и ждете, и ждете автобус конкретного маршрута, а затем вдруг к остановке подъезжают сразу три нужных вам автобуса. Оказывается, это не просто шутка: автобусы действительно имеют тенденцию собираться вместе. То же самое можно сказать и о землетрясениях. Например, сейсмологи зафиксировали сотни афтершоков всего за один месяц после землетрясения в Японии, случившегося в 2011 году.Еще в 1890-х годах японский сейсмолог Фусакити Омори установил, что частота этих повторных толчков уменьшается прямо пропорционально времени, прошедшего после основного толчка. То есть через месяц после землетрясения в сутки фиксируется в два раза больше афтершоков, чем через два месяца.

Таким образом, последовательность афтершоков, возникающих после основного толчка, также подчинена определенной закономерности. Здесь снова проявляется закон степенно́й зависимости, так как вероятность повторных толчков уменьшается в соотношении 1/t или t-1 (при достаточно больших значениях t). Степенны́е зависимости такого рода проявляются и в других областях: в сложной структуре поверхности изломов горной породы, в моделях роста живых организмов, в том, как пчелы и олени добывают свой корм. В каждом случае степенна́я зависимость указывает на наличие регулярности, скрытой за кажущейся случайностью событий, и дает подсказки о процессах, заложенных в их основе.

Все это важно потому, что финансовые рынки, по-видимому, функционируют подобным же образом.