Большинство людей не вспоминают о Южной Америке, когда думают о выдающихся физиках. Даже сами южноамериканцы удивляются, когда узнают, сколько замечательных физиков вышли из Аргентины, Бразилии и Чили. Даниэль Амати, Альберто Сирлин, Мигель Вирасоро, Гектор Рубинштейн, Эдуардо Фрадкин и Клаудио Тейтельбойм — это лишь некоторые из тех, кто серьезно повлиял на нашу науку.

Тейтельбойм, сменивший недавно имя на Клаудио Бунстер (см. сноску на с. 148), — особый человек, не похожий ни на кого из знакомых мне физиков. Его семья была очень близка к чилийскому социалистическому президенту Сальвадору Альенде и поэту-активисту, обладателю Нобелевской премии Пабло Неруде. Брат Клаудио Цезарь Бун стер возглавлял 7 сентября 1986 года группу, пытавшуюся убить бывшего фашистского диктатора генерала Аугусто Пиночета.

Клаудио — высокий темноволосый человек, с могучим, атлетически сложенным телом и свирепым пронизывающим взглядом. Несмотря на легкое заикание, он обладает обаянием и харизмой, которые могли бы сделать его великим политическим вождем. Он и в самом деле был антифашистским лидером небольшой группы ученых, помогавших в мрачные годы сохранить в живых чилийскую науку. Я не сомневаюсь, что в то время его жизнь находилась под угрозой.

Клаудио — человек потрясающих способностей и с легкой сумасшедшинкой. Будучи врагом военного режима в Чили, он любит всевозможную милитаристскую атрибутику. Живя в Техасе, перед возвращением в Чили он часто посещал выставки ножей и огнестрельного оружия и даже сегодня часто носит военную униформу.

Когда я в первый раз посетил его в Чили, он до смерти напугал меня, прикинувшись солдатом.

Это было в 1989 году, и вся власть еще принадлежала Пиночету. Когда мы с женой и нашим другом Вилли Фишлером сошли с самолета в Сантьяго, до зубов вооруженные люди в форме грубо согнали всех в длинную очередь на паспортный контроль. Клерки на контроле были военными, все при оружии, некоторые с автоматами. Пройти паспортный контроль было нелегко: длинная очередь едва двигалась и мы очень устали.

Вдруг, совершенно неожиданно, я увидел высокую фигуру в темных очках и военной униформе (или в чем-то похожем на униформу), прошедшую через оцепление и направляющуюся прямо к нам. Это был Клаудио, и он отдавал приказы солдатам так, словно был генералом.

Подойдя к нам, он взял меня за руку и, сделав надменный вид, провел нас мимо охраны, с властным видом махнув им рукой. Он подхватил наш багаж и быстро вывел нас из аэропорта к своему неправильно припаркованному джипу цвета хаки. Мы рванули из аэропорта в Сантьяго с такой скоростью, что порой машина вставала на два колеса. Каждый раз, проезжая мимо группы солдат, Клаудио отдавал им честь. «Клаудио, — прошептал я, — что это за безумие? Ты же нас убьешь». Но никто нас не остановил.

Последний раз я был в Чили уже после того, как на смену режиму Пиночета давно уже пришло демократическое правительство. У Клаудио были отличные связи с военными, особенно в авиации. Поводом для визита была конференция по черным дырам, организованная Клаудио и его небольшим институтом. Он использовал все свое влияние в военно-воздушных силах, чтобы свозить нашу компанию, включая Хокинга на самолете на чилийскую антарктическую базу. Мы получили массу удовольствия, но самым замечательным было то, как чилийские авиационные генералы, включая начальника штаба, нас обслуживали. Один генерал разливал чай, другой подносил закуску. Очевидно, Клаудио действительно обладал большим влиянием в Чили.

Но именно в 1989 году, во время автобусной экскурсии в чилийские Анды, Клаудио впервые рассказал мне о неких антидеситтеровских черных дырах. Сегодня их называют БТЗ-черными дырами по инициалам Банадоса, Тейтельбойма и Занелли. Макс Банадос и Йорг Занелли входили в ближайший круг Клаудио и сделали тогда открытие, оказавшее долгосрочный эффект на ход Битвы при черной дыре.

Физики, занимающиеся черными дырами, всегда мечтали уложить черную дыру в запечатанную шкатулку, надежно сохранив ее, подобно драгоценному украшению. Сохранив от чего? От испарения. Запечатывание в шкатулке — это что-то вроде закрывания крышкой котла с водой. Вместо того чтобы улетать в космос, частицы будут ударяться в стенки шкатулки (или в крышку котла) и падать обратно в черную дыру (или в котел).

Конечно, никто на практике не сможет поместить черную дыру в шкатулку, но такой мысленный эксперимент представляет интерес. Стабильная, неизменная черная дыра была бы намного проще испаряющейся. Но есть проблема: никакая реальная шкатулка не сможет вечно удерживать черную дыру. Как и все на свете, реальные шкатулки подвержены квантовой дрожи, и рано или поздно случится авария. Шкатулка войдет в контакт с черной дырой и — упс! — окажется в нее затянутой.

Здесь-тο и появляется антидеситтеровское пространство (АДС). Прежде всего, надо отметить, что, несмотря на свое название, антидеситтеровское пространство в действительности является пространственно-временным континуумом, одним из измерений которого служит время. Виллем де Ситтер был голландским физиком, математиком и астрономом, который открыл четырехмерное решение уравнений Эйнштейна, носящее его имя. Математически пространство де Ситтера — это экспоненциально расширяющаяся вселенная, которая растет во многом подобно тому, как это проис- ходит с нашей реальной Вселенной. Пространство де Ситтера долгое время считалось не более чем математической диковиной, но в последние годы оно приобрело огромное значение для космологов. Это искривленный пространственно-временной континуум с положительной кривизной, то есть сумма углов треугольника в нем больше 180 градусов. Но все это к делу не относится. В этот раз нас интересует не пространство де Ситтера, а антидеситтеровское пространство.

Антидеситтеровское пространство не было открыто антиматериальным двойником де Ситтера. Приставка «анти» указывает на то, что кривизна этого пространства отрицательная, а значит, сумма углов треугольника меньше 180 градусов. Самая интересная особенность АДС состоит в том, что оно обладает многими свойствами внутреннего пространства сферической шкатулки, но такой, которая не может быть проглочена черной дырой. Дело в том, что сферические стены АДС наделены мощной силой — непреодолимым отталкиванием, действующим на все, что к ним приближается, включая и горизонт черной дыры. Это отталкивание столь сильное что контакт между стенкой и черной дырой совершенно невозможен.

Обычное пространство-время имеет четыре измерения — три пространственных и одно временнóе. Физики иногда называют его четырехмерным, но это скрывает различие между пространством и временем. Более точно описывать пространство-время как (3 + 1) — мерное.

Флэтландия и Аайнландия — это тоже пространственно-временные континуумы. Флэтландия — мир лишь с двумя измерениями пространства, но его обитатели имеют чувство времени. Они должны корректно описывать свой мир как (2+1) — мерный. Лайнландцы, которые могут двигаться только вдоль одной оси, но также ощущают время, живут в (1 + 1) — мерном пространстве-времени. Замечательная особенность размерностей (2+1)и(1 + 1) состоит в том, что мы легко может изображать такие пространства на картинках, что помогает нашей интуиции.

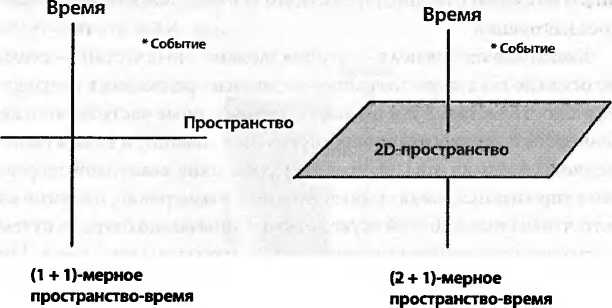
Конечно, ничто не мешает математическим физикам изобретать миры с любым числом пространственных измерений, несмотря на неспособность мозга их визуализировать. Однако интересно, можно ли изменить число временных измерений? В чисто абстрактном математическом смысле ответ — да, но он, похоже, не имеет большого смысла с физической точки зрения. Одно измерение выглядит вполне подходящим значением.

Антидеситтеровские пространства могут быть разной размерности. У них может быть любое число пространственных направлений, но только одно временнбе. То АДС, с которым работали Банадос, Тейтельбойм и Занелли, было (2 + 1) — мерным, что позволяет легко все объяснить на картинках.

Трехмерное пространство (не пространство-время) — это одна из тех вещей, которая кажется жестко прошитой в нашей когнитивной системе. Никто не может визуализировать четырехмерное пространство без опоры на абстрактную математику. Может показаться, что одно- и двумерные пространства изобразить проще, и, в определенном смысле, так и есть. Но если вы на мгновение задумаетесь, то поймете, что, визуализируя линии и плоскости, вы всегда представляете их вложенными в трехмерное пространство. Это почти наверняка связано с тем, как эволюционировал наш мозг, и не имеет никакого отношения к особым математическим свойствам трех измерений.

Квантовая теория поля — теория элементарных частиц — столь же осмысленна в мире с меньшим числом измерения, как в трехмерном пространстве. Судя по всему, элементарные частицы вполне возможны в двумерном пространстве (Флэтландии) и даже в одномерном (Аайнландии). Фактически уравнения квантовой теории поля упрощаются, когда уменьшается число измерений, и многое из того, что мы знаем об этой науке, было первоначально открыто путем изучения квантовой теории поля в подобных модельных мирах. Так что ничего необычного в том, что Банадос, Тейтельбойм и Занелли изучали вселенную всего с двумя измерениями, не было.

Лучший способ объяснить АДС — тот, что предложил Клаудио во время чилийской автобусной экскурсии: на картинках. Не будем пока думать о времени и начнем с обычного пространства внутри пустой круглой шкатулки. В трех измерениях ее внутренняя область будет сферической; в двух измерения она еще проще и имеет форму круга.

Теперь добавим время. Когда оно отложено по вертикальной оси, пространственно-временной континуум напоминает внутреннюю область цилиндра. На рисунке АДС — это незакрашенная внутренность цилиндра.

Представим себе срезы АДС (напоминаю, они имеют два измерения) по аналогии с тем, как мы нарезали черную дыру при построении диаграммы вложения. Нарезание выделяет сечения, о которых можно сказать, что они именно пространственные.

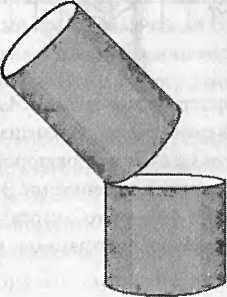
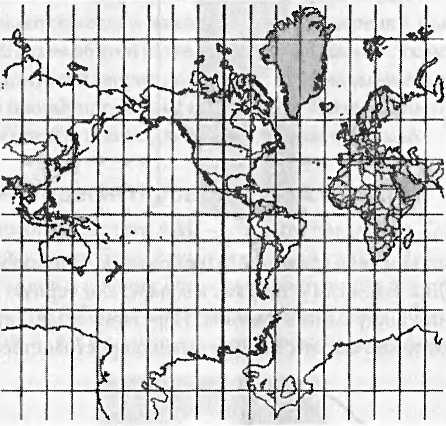
Давайте изучим двумерный срез немного внимательнее. Как и следовало ожидать, он искривлен в чем-то подобно земной поверхности. Это означает, что, рисуя его на плоскости (на листе бумаги), вы будете растягивать и искажать поверхность. Невозможно нарисовать карту Земли на плоском листе бумаги без серьезных искажений. Области, близкие к северному и южному краям карты в проекции Меркатора, значительно увеличены сравнительно с областями вблизи экватора. Гренландия выглядит такой же большой, как Африка, хотя в действительности площадь Африки примерно в пятнадцать раз больше.

Пространство (а также пространство-время) в АДС искривлено, но в отличие от земной поверхности его кривизна отрицательна. Растягивание его на плоскости дает «антимеркаторовский» эффект: области на краях выглядят слишком маленькими. Знаменитый рисунок Эшера «Предел — круг 4» — это «карта» пространства с отрицательной кривизной, которая показывает, как именно выглядит двумерный срез АДС.

Я нахожу «Предел — круг 4» по меньшей мере гипнотическим. (Он напоминает мне бесконечный поиск последней видимой собаки персонажами романа «Мышонок и его отец», см. главу 20.) Ангелы и демоны нескончаемо повторяются, переходя в бесконечный фрактальный край. Заключил ли Эшер сделку с дьяволом, позволившую ему нарисовать бесконечное число ангелов? Или, если я как следует пригляжусь, то смогу заметить последнего видимого ангела?

Задержимся на мгновение для перепрошивки своих представлений: вам должно стать видно, что все ангелы и демоны имеют одинаковые размеры. Это не просто маленькое ментальное упражнение, оно помогает запомнить, что Гренландия почти в точности равна по размерам Аравийскому полуострову, несмотря на то что в проекции Меркатора выглядит в восемь раз крупнее. По-видимому, в голове у Эшера эти ментальные упражнения были прошиты очень хорошо, но, попрактиковавшись, вы тоже смажете приобрести такой навык.

Теперь добавим время и сведем воедино всю картину антидеситтеровского пространства. Как обычно, отложим время по вертикальной оси. Каждый горизонтальный срез представляет собой обычное пространство в определенный момент. Рассматривайте АДС как бесконечное число слоев пространства — тонкую нарезку бесконечной салями, — которая, будучи сложена в стопку, образует пространственно-временной континуум.

Пространство в АДС причудливо искривлено, но не более чем время. Напомню, что, как мы узнали в главе 3, часы, находящиеся в разных местах, согласно общей теории относительности, часто идут в разном темпе. Например, замедление хода часов вблизи горизонта черной дыры позволяет использовать ее в качестве машины времени. Часы в АДС тоже ведут себя странно. Представьте, что у каждого эшеровского демона есть наручные часы. Если ближайшие к центру демоны оглянутся на своих чуть более далеких соседей, они заметят нечто странное: часы у тех идут примерно вдвое быстрее. Если предположить, что у демонов есть метаболизм, то у внешних соседей обмен веществ тоже будет протекать быстрее. Каждый следующий ряд будет быстрее предыдущего, пока вблизи границы часы не станут идти так быстро, что для центральных демонов все сольется в кружащийся туман.

Кривизна пространства-времени в АДС создает гравитационное поле, которое притягивает объекты к центру, даже если там ничего нет. Одно из проявлений этого призрачного гравитационного поля состоит в том, что если массу сместить в сторону границы, ее будет тянуть назад, почти как если бы она была на пружине. Предоставленная самой себе масса будет бесконечно колебаться вперед и назад. Другой эффект, по сути, является оборотной стороной медали: притяжение к центру ничем не отличается от отталкивания границей. Это отталкивание — непреодолимая сила, которая удерживает всё, включая черные дыры, от соприкосновения с границей.

Шкатулки делаются для того, чтобы класть в них вещи, поэтому положим внутрь несколько частиц. Оказавшись внутри, они станут притягиваться к центру. Отдельная частица будет вечно колебаться вокруг него, но при наличии двух или более частиц они могут сталкиваться. Гравитация — не призрачная гравитация АДС, а обычное гравитационное взаимодействие между частицами — может заставить их собраться в сгусток. Добавление частиц будет увеличивать давление и температуру в центре, и сгусток может зажечься, образовав звезду. Добавление еще большей массы приведет в конце концов к катастрофическому коллапсу: образуется черная дыра — черная дыра, заключенная в шкатулку.

Банадос, Тейтельбойм и Занелли были не первыми, кто изучал черные дыры в АДС; эта честь принадлежит Дону Пейджу и Стивену Хокингу. Однако БТЗ открыли их простейший пример, который просто визуализировать, поскольку пространство имеет только два измерения. Вот воображаемый снимок БТЗ-черной дыры. Край черной области — это горизонт.

За одним исключением антидеситтеровские черные дыры обладают всеми свойствами обычных. Как всегда, противная сингулярность скрывается за горизонтом. Добавление массы увеличивает размеры черной дыры, приближая ее горизонт к внешней границе.

Но, в отличие от обычных черных дыр, АДС-версия не испаряется. Горизонт — это бесконечно горячая поверхность, которая постоянно испускает фотоны. Но фотонам некуда уходить. Вместо испарения в пустое пространство они падают обратно в черную дыру.

Представьте, что вы всматриваетесь в граничную точку рисунка «Предел — круг 4» и затем раздуваете рисунок так, что его край выглядит совершенно прямым.

Мы можем повторять это снова и снова, никогда не исчерпав ангелов и демонов, пока в пределе край не станет выглядеть совершенно прямым и бесконечным. Я — не Эшер и не буду пытаться рисовать его изящных созданий. Я упрощу их настолько, что демоны превратятся в квадраты, а картина станет напоминать решетку из всё уменьшающихся по мере приближения к границе квадратов. Думайте об АДС как о бесконечной кирпичной стене. При спуске вниз по стене кирпичи удваиваются в размерах с каждым новым рядом.

Конечно, в антидеситтеровском пространстве не будет реальных линий, так же как нет линий долготы и широты на поверхности Земли. Они проведены здесь лишь для того, чтобы наглядно показать, как искажаются размеры из-за кривизны пространства.

Эшеровский рисунок и моя грубая версия представляют двумерное пространство, но реальное пространство — трехмерно. Нетрудно представить, как будет выглядеть пространство, если добавить еще одно измерение (не временное). Все, что нужно сделать, — это заменить квадраты сплошными трехмерными кубами. На следующей картинке я изобразил небольшой участок такой трехмерной «кирпичной стены». Но не забывайте, что она тянется бесконечно как в горизонтальном, так и в вертикальном направлении.

Добавление к этой картине времени производится так же, как и раньше: каждый квадрат или куб оснащается своими собственными часами. Скорость хода часов зависит от того, в каком слое они расположены. Каждый раз, когда мы придвигаемся на один слой ближе к границе, часы ускоряются в два раза. И напротив, когда мы спускаемся вниз по стене, часы замедляются.

С математической точки зрения нет причин останавливаться на трехмерном пространстве. Складывая друг на друга четырехмерные кубы меняющихся размеров, можно построить (4+1) — мерное антидеситтеровское пространство и так далее для любого числа измерений. Но нарисовать даже один четырехмерный куб весьма сложно. Вот одна такая попытка.

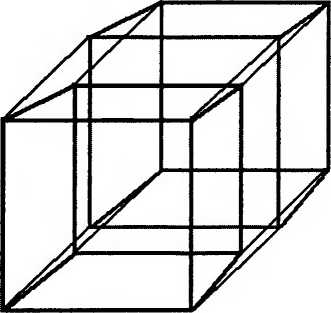
Если сложить их друг на друга и попытаться нарисовать четырехмерную версию АДС, получится ужасная мешанина.

Прекращение испарения черных дыр — достойная причина для изучения физики внутри шкатулки. Но идея мира в шкатулке гораздо интереснее. Подлинная цель состоит в понимании голографического принципа и доведении его до математической точности. Вот как я объяснял голографический принцип в главе 18: «Трехмерный мир нашего обыденного опыта — Вселенная, заполненная галактиками, звездами, планетами, домами, камнями и людьми, — это голограмма, образ реальности, закодированной на далекой двумерной поверхности. Этот новый закон физики, называемый голографическим принципом, утверждает, что всё, находящееся внутри некоторой области пространства, можно описать посредством битов информации, расположенных на ее границе».

Отчасти неточность формулирования голографического принципа связана с тем, что предметы могут проходить через границу. В конце концов, это ведь воображаемая математическая поверхность безо всякой реальной материи. Сама возможность для объектов входить в рассматриваемую область и покидать ее затуманивает смысл слов «всё, находящееся внутри некоторой области пространства, можно описать посредством битов информации, расположенных на ее границе». Но мир в шкатулке с идеально непроницаемыми стенами избавлен от этой проблемы. Новая формулировка будет такой:

Во время чилийской автобусной экскурсии 1989 года я не понял, почему Клаудио Тейтельбойм так восхищался антидеситтеровским пространством. Черные дыры в шкатулке — ну и что? Мне понадобилось восемь лет, чтобы уловить суть, — восемь лет и еще один южноамериканский физик, на этот раз аргентинский.

Хуан Малдасена — полная противоположность Клаудио Тейтельбойму. Он невысок и гораздо хладнокровнее. Я не могу себе представить его гоняющим на автомобиле по Сантьяго в поддельной военной форме. Но как у физика у него нет недостатка в храбрости. В 1977 году он поставил себя под удар, сделав невероятно смелое заявление, которое казалось почти таким же сумасшедшим, как моя дикая поездка с Клаудио. Фактически Малдасена доказывал, что два математических мира, которые кажутся совершенно непохожими, на самом деле являются в точности и одним и тем же. Один мир имел четыре пространственных измерения и одно временное (4 + 1), другой был (3 + 1) — мерным и больше напоминал мир нашего повседневного опыта. Я возьму на себя смелость упростить эту историю, с тем чтобы ее было проще визуализировать, и в каждом случае уменьшу количество измерений на одно. Поэтому я буду говорить, что некоторая воображаемая версия Флэтландии — (2 + 1) — мерного мира — в определенном смысле эквивалентна антидесситтеровскому миру с (3 + 1) измерениями.

Как такое вообще возможно? Самое явное свойство пространства — это количество его измерений. Неспособность распознавать размерность пространства означала бы крайне опасную степень нарушения восприятия. Безусловно, нельзя перепутать два измерения с тремя, находясь в здравом уме. По крайней мере, так кажется. Путь, который привел Малдасену к его открытию, был запутанной и извилистой тропинкой, которая проходила через экстремальные черные дыры, D-браны и нечто, называемое матричной теорией, и в конце приводила к голографическому принципу.

Отправной точкой были D-браны Полчински. Напомню, что D-брана — это материальный объект, который в зависимости от размерности может быть точкой, линией, поверхностью или объемом, заполняющим пространство. Главное свойство, отличающее D-браны от всего остального, состоит в том, что на них могут заканчиваться фундаментальные струны. Для определенности давайте сосредоточимся на D2-бpaнax. Представьте себе плоскую двумерную поверхность, плавающую в трехмерном пространстве, подобно магическому паркету. Открытые струны могут присоединяться к этой D-бране обоими своими концами. Они способны скользить вдоль D-браны, но не могут свободно перепрыгивать в третье измерение. Кусочки струн, словно на коньках без трения, катятся по метафорическому льду, будучи неспособным оторвать от него ноги. Издали каждый кусочек струны выглядит как частица, движущаяся в двумерном мире. Если струн больше одной, они могут сталкиваться, рассеиваться друг на друге и даже сливаться в более сложные объекты.

D-браны могут существовать по отдельности, но они липкие. Если аккуратно их сблизить, они сцепятся и образуют составную брану из нескольких слоев, как на следующем рисунке.

Я нарисовал D-браны на некотором расстоянии друг от друга. Но когда они сливаются, промежуток исчезает. Группу слипшихся вместе D-бран называют D-бранной стопкой.

Свойства открытых струн, движущихся по D-бранной стопке, богаче и разнообразнее, чем у струн, движущихся по одиночной D-бране. Два конца струны могут присоединиться к разным элементам стопки, как если бы два конька двигались по двум немного разным уровням. Чтобы различать браны, им можно дать имена. Например, в нарисованной выше стопке можно назвать браны красной, зеленой и синей.

Концы струн, которые катятся по D-бранной стопке, должны быть всегда присоединены к D-бране. Например, струна может быть обоими концами присоединена к красной бране. Тогда это будет красно-красная струна. Аналогично могут быть сине-синие и зелено-зеленые струны. Но возможно также, что два конца струны присоединены к разным бранам. Так получаются красно-зеленые струны, красно-синие и т. д. Всего имеется девять разных возможностей для движения струн по этой D-бранной стопке.

Интересные вещи начинаются, когда к бранам присоединено несколько струн.

Струны на Б2-бранной стопке очень похожи на обычные частицы, но только в мире, имеющем два пространственных измерения. Они взаимодействуют друг с другом, рассеиваются при столкновениях и оказывают силовое воздействие на находящиеся поблизости струны. Одна струна может распасться на две. На следующей серии рисунков показано, как струна на одиночной бране разделяется и превращается в две струны.

Точка на исходной струне соприкасается с браной, что позволяет струне разделиться, но непременно так, чтобы все концы были присоединены к бранам. Предыдущий рисунок можно также просматривать снизу вверх, и тогда получится, что пара струн сливается и образует одну.

А вот последовательность кадров со струнами на стопке из трех D-бран. Здесь показано, как красно-зеленая струна сталкивается с зелено-синей. Две струны сливаются и образуют одну красносинюю струну.

Красно-красная струна не может слиться с зелено-зеленой, поскольку их концы никогда не соприкоснутся.

Не правда ли, мы уже видели нечто подобное? Ну конечно, если вы прочли главу 19. Правила, управляющие поведением струн, присоединенных к стопке D-бран, в точности такие же, что управляют глюонами в квантовой хромодинамике (КХД). В главе 19 я объяснял, что глюон подобен небольшому линейному магниту с двумя концами, каждый из которых помечен своим цветом. Сходство на этом не заканчивается. Приведенный выше рисунок, показывающий соединение двух струн в одну, очень похож на диаграмму глюонного узла в КХД.

Эта параллель между «физикой на D-бране» и обычным миром элементарных частиц — замечательный факт, который, как мы увидим в следующей главе, оказался чрезвычайно полезным. Когда физики находят два разных способа описания одной системы, они называют такие два описания «дуальными». Пример тому дуальное описание света как волн или частиц. Физика полна дуальностей, и не было ничего особенно неожиданного или нового в самом факте, что Малдасена открыл два дуальных описания струн на D-бране. Что было новым, почти неслыханным, так это то, что эти две картины описывали миры с разным числом пространственных измерений.

Я уже намекал на одно такое описание: (2-1-1) — мерная флэтландская версия КХД. Она описывает плоские протоны, мезоны и глюболы, но, как и настоящая КХД, не содержит и следа гравитации. Другая сторона этой дуальности — альтернативного способа представления одних и тех же вещей — описывает мир трехмерного пространства, причем не любого, а именно антидесситтеровского. Малдасена доказал, что флэтландская КХД дуальна (3 + 1) — мерной антидесситтеровской вселенной. Более того, в этом трехмерном мире материя и энергия служат источником гравитационных сил, так же как и в реальном мире. Другими словами, мир (2 + 1) измерений, включающий КХД, но без гравитации, эквивалентен вселенной с (3 + 1) измерением и гравитацией.

Как такое возможно? Как может мир всего с двумя измерениями быть в точности таким же, как трехмерный? Откуда появляются дополнительные измерения пространства? Ответ кроется в искажениях антидесситтеровского пространства, заставляющих объекты вблизи границы выглядеть маленькими по сравнению с такими же объектами во внутренней части пространства. Эти искажения воздействуют на воображаемых демонов, но также и на реальные объекты при их движении в пространстве. Например, если взять букву «А» метрового размера и заставить ее отбрасывать тень на границу, то получаемое изображение будет сжиматься или увеличиваться по мере приближения и удаления объекта от границы.

С точки зрения трехмерной внутренней области это — иллюзия, не более реальная, чем огромные размеры Гренландии на карте в проекции Меркатора. Но в дуальном описании — флэтландской теории — нет понятия расстояния в перпендикулярном, третьем измерении, заменой ему служит понятие размера. Это очень неожиданная математическая связь: рост и уменьшение размеров во флэтландской половине дуальности — это в точности то же самое, что движение вперед и назад вдоль третьего измерения в другой составляющей этой дуальности.

И вновь мы видим нечто знакомое, на этот раз из главы 18, где мы открыли, что наш мир — это что-то вроде голограммы. Два дуальных описания Малдасены являли собой голографический принцип в действии. Все, что происходит во внутренней области антидеситтеровского пространства, — «это голограмма, образ реальности, закодированной на далекой двумерной поверхности». Трехмерный мир с гравитацией — это эквивалент двумерной квантовой голограммы на границе пространства.

Я не знаю, провел ли Малдасена параллель между своим открытием и голографическим принципом, но Эд Виттен вскоре ее заметил. Всего через два месяца после статьи Малдасены Виттен опубликовал в Интернете свою собственную статью под заголовком «Антидеситтеровское пространство и голография».

Из всего содержания виттеновской статьи мое особое внимание привлек раздел о черных дырах. Антидеситтеровское пространство, его оригинальная версия, а не уплощенная стена из кирпичей, — подобно консервной банке с супом. Горизонтальные срезы банки представляют пространство; вертикальная ось банки — это время. Этикетка на ее внешней поверхности — это граница, а внутренняя область — это сам пространственно-временной континуум.

Чистое АДС-пространство подобно пустой консервной банке, но его можно сделать интереснее, наполнив «супом», то есть материей и энергией. Виттен объяснял, что, закачав в банку достаточное количество массы и энергии, можно создать черную дыру. Отсюда возникает вопрос. Согласно Малдасене, должно быть и второе — дуальное — описание, которое не упоминает о том, что содержится внутри банки. Это альтернативное описание формулируется в терминах двумерной квантовой теории поля для частиц, подобных глюонам, которые движутся по этикетке. Наличие черной дыры в супе может быть эквивалентно определенной особенности граничной голограммы, но что это за особенность? В граничной теории Виттен доказал, что черная дыра в супе эквивалентна обычной горячей жидкости из элементарных частиц — в сущности, просто глюонов.

В момент, когда я увидел статью Виттена, я понял, что Битва при черной дыре окончена. Квантовая теория поля — это частный случай квантовой механики, а информация в квантовой механике никогда не уничтожается. Что еще сделали Малдасена и Виттен, так это доказали, не оставив ни тени сомнения, что информация никогда не должна теряться за горизонтом черной дыры. Струнные теоретики могли понять это сразу; релятивистам понадобилось немного больше времени. Но война завершилась.

Хотя Битва при черной дыре должна была окончиться еще в начале 1998 года, Стивен Хокинг уподобился тем несчастным солдатам, которые годами скрывались в джунглях, не зная, что военные действия прекратились. Но на этот раз он стал трагической фигурой. Пятидесятишестилетний, уже прошедший пик своей интеллектуальной формы и почти неспособный общаться, Стивен не улавливал сути дела. Уверен, что это не было связано с ограниченностью его интеллекта. Из тех контактов, которые у меня были с ним после 1998 года, стало ясно, что его разум остается исключительно острым. Но его физические возможности настолько ослабли, что он оказался почти полностью замкнут в собственной голове. Не имея возможности записывать уравнения и испытывая колоссальные трудности при общении с коллегами, он должен был столкнуться с тем, что не может проделать те вещи, которые обычно выполняют физики, чтобы разобраться в новой, незнакомой им работе. Поэтому Стивен еще некоторое время продолжал борьбу.

Вскоре после публикации статьи Виттена в Санта-Барбаре состоялась еще одна конференция, на этот раз чтобы отметить голографический принцип и открытие Малдасены. Послеобеденным докладчиком был Джефф Харвей (Н из CGHS), однако вместо речи он призвал всех исполнить победную песнь «Малдасена», которая поется и танцуется на манер «Макарены».