Книга: Битва при черной дыре. Мое сражение со Стивеном Хокингом за мир, безопасный для квантовой механики
Назад: 18 Мир как голограмма
Дальше: 20 Аэроплан Алисы, или Последний видимый пропеллер
Часть IV
Кольцо смыкается
19
Оружие массового убеждения
В действительности я не готов, пожалуй, называть теорию струн «теорией», скорее, «моделью», или даже так: это просто догадка. В конце концов, теория должна сопровождаться указаниями о том, как действовать для выявления вещей, которые она описывает, в нашем случае — элементарных частиц, и, хотя бы в принципе, она должна позволять сформулировать правила для вычисления свойств этих частиц и получения относительно них новых предсказаний. Представьте, что я даю вам кресло, поясняя, что ножек у него пока нет, а сиденье, спинка и подлокотники, возможно, скоро будут доставлены; что бы я вам ни вручил, могу ли я называть это креслом?— Герард 'т Хоофт
Самого по себе голографического принципа было недостаточно для победы в Битве при черной дыре. Он был недостаточно строгим и не имел надежного математического основания. Реакцией на него был скептицизм: мир как голограмма? Похоже на научную фантастику. Выдуманный физик Стив в далеком будущем переходит в «иной мир», а император с графом в это же время наблюдают за его уничтожением. Напоминает спиритизм.
Почему маргинальная идея, годами лежащая без использования, неожиданно склонят чашу весов в свою пользу? В физике подобное нередко случается безо всякого предупреждения. Важное и яркое событие неожиданно привлекает внимание критической массы физиков, и за короткое время странное, фантастическое, немыслимое становится обычным.
Иногда толчком становится экспериментальный результат. Эйнштейновская корпускулярная теория света медленно завоевывала признание, поскольку большинство физиков надеялось, что какой-то новый поворот событий спасет в итоге волновую теорию. Однако в 1923 году Артур Комптон изучил рассеяние рентгеновских лучей на атомах углерода и показал, что набор углов и энергий в точности соответствует столкновению частиц. Между исходным утверждением Эйнштейна и экспериментом Комптона прошло восемнадцать лет, но потом всего за несколько месяцев сопротивление корпускулярной теории света рассеялось.
Математический результат, особенно если он неожиданный, тоже может послужить таким катализатором. Базовые элементы Стандартной модели (физики элементарных частиц) датируются серединой 1960-х годов, но имелись доводы (некоторые из них были выдвинуты создателями теории) о том, что ее математические основания внутренне противоречивы. Затем в 1971 году молодой, никому не известный аспирант выполнил чрезвычайно сложные и тонкие вычисления и объявил, что эксперты ошибались. За очень короткое время Стандартная модель стала действительно стандартной, а неизвестный студент — Герард 'т Хоофт — стал в мире физики самой яркой звездой.
Другой пример того, как математика может качнуть весы в пользу сумасбродной идеи, — это расчет Стивеном Хокингом температуры черной дыры. Первой реакцией на утверждение Бекенштейна о том, что черные дыры имеют энтропию, был скептицизм, доходящий до насмешек, в том числе со стороны Хокинга. В ретроспективе аргументы Бекенштейна выглядят блестящими, но в то время они были слишком туманны и приблизительны для признания, да еще и вели к абсурдному заключению: черные дыры испаряются. Именно технически сложные вычисления Хокинга сдвинули парадигму черных дыр от холодных мертвых звезд к объектам, высвечивающим свое собственное внутреннее тепло.
Описанные мной переломные события имеют ряд общих особенностей. Во-первых, они были неожиданными. Совершенно непредвиденный результат, будь он экспериментальным или математическим, — это мощный концентратор внимания. Во-вторых, в случае математического результата, чем он более технический, точный, неинтуитивный и трудный, тем сильнее он толкает людей к признанию значения нового способа мышления. Отчасти причина в том, что в сложных вычислениях много мест, где может таиться ошибка. Трудно игнорировать случаи, когда этих опасностей удается избежать. Это можно отнести и к вычислениям ’т Хофта, и к вычислениям Хокинга.
В-третьих, парадигмы меняются, когда новые идеи создают другим исследователям обширное поле для более привычной работы. Физики всегда находятся в поисках новых идей, над которыми стоило бы поработать, и набрасываются на все, что открывает возможности для проведения собственных исследований.
Дополнительность черных дыр и голографический принцип, безусловно, были неожиданными, даже шокирующими, но сами по себе они не обладали двумя другими свойствами, по крайней мере еще не обладали. В 1994 году казалось, что вопрос об экспериментальном подтверждении голографического принципа не стоит даже обсуждать, равно как и возможность его убедительного математического обоснования. Но на деле и то и другое было ближе, чем кто-либо мог себе представить. Всего за два года начала обретать форму точная математическая теория, а спустя еще десятилетие стала открываться возможность восхитительного экспериментального подтверждения. И все это благодаря теории струн.
Прежде чем перейти к более подробному рассказу о теории струн, позвольте мне обрисовать общую картину. Никто не знает наверняка, правильно ли теория струн описывает наш мир, и, возможно, мы еще много лет этого не узнаем. Но для наших целей это не самый важный вопрос. У нас есть впечатляющие подтверждения того, что теория струн является математически непротиворечивой теорией некоего мира. Она основывается на принципах квантовой механики; она описывает систему элементарных частиц, подобных тем, что имеются в нашем мире; и в ней в отличие от других теорий (в первую очередь имеется в виду квантовая теория поля) все материальные объекты взаимодействуют посредством гравитационных сил. А самое главное, в теории струн есть черные дыры.
Но как с помощью теории струн доказывать какие-либо свойства нашего мира, если мы не уверены, что она верна? Для некоторых задач это не имеет значения. Мы используем теорию струн в качестве модели некоторого мира, а затем вычисляем или математически доказываем, теряется ли информация в черных дырах этого мира.
Допустим, мы обнаружили, что информация в нашей модели не теряется. Убедившись в этом, можно внимательнее присмотреться и понять, в чем же был неправ Хокинг. Можно попытаться понять, имеют ли место дополнительность черных дыр и голографический принцип в теории струн. Если да, то это не доказывает, что теория струн верна, но доказывает, что Хокинг ошибался, поскольку он объявил доказанным, что черные дыры должны уничтожать информацию в любом непротиворечивом мире.
Свое объяснение теории струн я намерен ограничить минимально необходимыми основами. Подробнее о ней можно узнать в целом ряде изданий, включая мою книгу «Космический ландшафт», а также книги Брайана Грина «Элегантная Вселенная» и Айзы Рэнделл «Закрученные пассажи». Теория струн была почти случайным открытием. Первоначально она не имела никакого отношения к черным дырам и далекому планковскому миру квантовой гравитации. Она касалась куда более обыденных вопросов, связанных с адронами. Хотя слово «адрон» не используется в повседневном обиходе, сами адроны входят в число самых распространенных и хорошо изученных элементарных частиц. К ним относятся протоны и нейтроны — частицы, из которых состоят атомные ядра, — а также их близкие родственники, называемые мезонами, и так называемые глюболы. В свое время адроны были передним краем физики элементарных частиц, но сегодня они часто воспринимаются как старомодная тема в ядерной физике. Тем не менее в главе 23 мы познакомимся с рядом идей, которые возвращают адронам их былую славу в физике.
Элементарно, мой дорогой Ватсон
Есть старый анекдот о двух еврейских дамах, которые встретились на углу в Бруклине. Одна говорит другой: «Tы должна уже знать, что мой сын стал доктором. А между прочим, кем стал твой сын, у которого вечно были трудности с математикой?» Другая ей отвечает: «О, мой мальчик стал гарвардским профессором по физике элементарных частиц». Первая с сочувствием отвечает: «Да, дорогая, ужасно жаль, что он так и не дослужился до физики высших частиц».
Что в точности имеется в виду под элементарными частицами и какими они еще могут быть? Простейший ответ: частица элементарна, если она столь мала и проста, что ее нельзя разделить на меньшие части. Их противоположность — не высшие, а составные частицы — те, что состоят из более простых частей меньшего размера.
Редукционизм — это научная философия, которая приравнивает понимание к разбиранию вещей на части. До сих пор это очень хорошо работало. Молекулы объясняются как состоящие из атомов; в свою очередь атомы — это совокупности отрицательно зараженных электронов, обращающихся вокруг центрального положительно заряженного ядра; ядра оказались сгустками нуклонов; наконец, каждый нуклон состоит из трех кварков. Сегодня все физики согласны, что молекулы, атомы, ядра и нуклоны — составные объекты.
Однако некоторое время назад каждый из них считался элементарным. В действительности термин «атом» происходит от греческого слова, означающего «неделимый», которое было в ходу около 2500 лет. Лишь недавно Эрнест Резерфорд открыл атомное ядро. Оно казалось настолько маленьким, что могло считаться просто точкой. Как видите, то, что одно поколение называет элементарным, потомки могут счесть составным.
Все это поднимает вопрос о том, как мы решаем — по крайней мере в данный момент, — является некая частица элементарной или составной? Вот один из возможных ответов: столкните два таких объекта с достаточной силой и посмотрите, что разлетится. Если что-то вылетит, оно должно было находиться внутри одной из первоначальных частиц. В действительности, когда сталкиваются два очень быстрых электрона, во все стороны разлетается куча всевозможного мусора. Особенно много будет фотонов, электронов и позитронов. Если столкновение очень сильное; то появятся также протоны, нейтроны и их античастицы. И для полноты картины иногда может появиться целый атом. Означает ли это, что электроны состоят из атомов? Очевидно, нет. Столкновения с огромными энергиями помогают разобраться в свойствах частиц, но, оказывается, то, что при этом вылетает, не всегда позволяет судить, из чего эти частицы состоят.
Вот более удачный метод выяснения, состоит ли нечто из частей. Начнем с очевидно составного объекта — камня, баскетбольного мяча или куска теста для пиццы. С таким предметом можно много чего сделать — сжать его до меньшего объема, деформировать, придав ему новую форму, или закрутить его вокруг собственной оси. На сжатие, изгиб или закручивание требуется энергия. Например, вращающийся мяч обладает кинетической энергией; чем быстрее ои крутится — тем больше энергия. А поскольку энергия — это масса, быстро вращающийся мяч становится массивнее. Мерой вращения служит угловой момент, который учитывает скорость вращения мяча, его размер и массу. Приобретая все больший и больший угловой момент, мяч накапливает энергию. На следующем графике показано, как нарастает энергия вращающегося баскетбольного мяча.
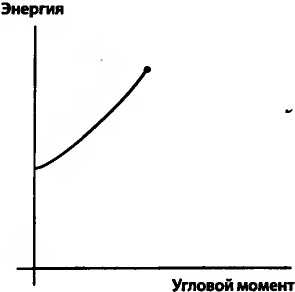
Вращающийся баскетбольный мяч
Но почему эта кривая неожиданно обрывается? Догадаться нетрудно. Материал, из которого сделан мяч (кожа или резина), не может выдержать слишком большого натяжения. В какой-то момент мяч будет разорван на части центробежными силами.
Теперь представьте себе частицу размером не больше точки в пространстве. Как заставить математическую точку вращаться вокруг своей оси? Или что бы могло означать изменение ее формы? Возможность придать объекту вращение или заставить его пульсировать — это признак того, что он состоит из меньших частей, частей, которые движутся друг относительно друга.
Молекулы, атомы и ядра тоже можно раскрутить, но в случае этих микроскопических шариков материи центральную роль играет квантовая механика. Как и во всех колебательных системах, энергия и угловой момент могут увеличиваться только дискретными шагами. Раскручивание ядра — это не процесс постепенного накачивания его энергией. Это больше похоже на подталкивание вверх по лестнице. Так что график энергии и углового момента представляет собой последовательность отдельных точек.
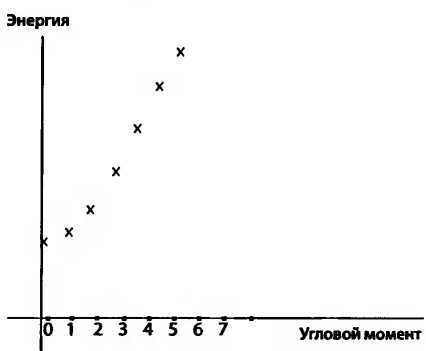
Вращающееся ядро
Если не считать дискретности шагов, график выглядит в основном так же, как и для баскетбольного мяча, включая и внезапный обрыв. Как и мяч, ядро выдерживает лишь определенную центробежную силу, а потом разлетается на части.
А что можно сказать об электронах? Можно ли их раскрутить? Несмотря на все усилия, а они на протяжении многих лет были довольно значительными, никому не удалось увеличить угловой момент электрона. Мы еще вернемся к электронам, но сначала давайте займемся адронами — протонами, нейтронами, мезонами и глюболами.
Протоны и нейтроны очень похожи. У них почти одинаковая масса, а силы, которые связывают их в ядра, практически идентичны. Единственное существенное различие состоит в том, что протон имеет небольшой электрический заряд, а нейтрон, как и указывает его название, электрически нейтрален. Как будто нейтрон — это протон, которому каким-то образом удалось скрыть свой заряд. Именно это сходство привело физиков к тому, чтобы терминологически объединить эти частицы в один объект — нуклон. Протон — это положительный нуклон, а нейтрон — нейтральный нуклон.
В эпоху зарождения ядерной физики нуклон, хотя он почти в 2000 раз тяжелее электрона, также считался элементарной частицей. Но по части простоты нуклон не имеет ничего общего с электроном. По мере развития ядерной физики объекты размером в 100 000 раз меньше атомов стали считаться не такими уж маленькими. Тогда как электрон остается точкой в пространстве — по крайней мере, на современном уровне знаний, — нуклон демонстрирует богатую, сложную внутреннюю механику. Оказывается, у нуклонов гораздо меньше общего с электронами, чем с ядрами, атомами и молекулами. Протоны и нейтроны — это конгломераты из множества меньших объектов. Мы знаем об этом, поскольку они вращаются, вибрируют и могут менять свою форму.
Точно так же как для баскетбольного мяча, для атомного ядра можно построить график, на котором по горизонтальной оси отложено вращение, то есть угловой момент нуклона, а его энергия — по вертикальной. Когда сорок лет назад это было сделано впервые, получившийся график удивил своей простотой: последовательность точек легла почти точно на прямую линию. Еще удивительнее было то, что у нее не наблюдалось конца.

Вращающийся нуклон
Такая диаграмма несет важную информацию о внутреннем устройстве нуклона. Две отмеченные особенности имеют огромное значение для тех, кто знает, как прочитать скрытое в них послание.
Сам факт, что нуклон может вращаться вокруг своей оси, указывает на то, что это не точечная частица; он состоит из частей, способных двигаться друг относительно друга. Но тут скрывается нечто большее. Вместо того чтобы неожиданно обрываться, последовательность, похоже, продолжается неограниченно, а значит, нуклон не разваливается, когда вращается слишком быстро. То, что удерживает его части вместе, намного мощнее сил, скрепляющих атомное ядро.
Неудивительно, что при вращении нуклон растягивается, но делает он это не так, как вращающийся кусок теста для пиццы, который превращается в двумерный блин.

Расположение точек в виде прямой линии указывает на то, что нуклон растягивается в длинный тонкий эластичный струноподобный объект.

Полвека экспериментов с нуклонами принесли уверенность в том, что это эластичные струны, которые могут растягиваться, вращаться и вибрировать, когда возбуждаются дополнительной энергией. На самом деле все адроны можно растянуть в длинные струноподобные объекты. Очевидно, все они сделаны из одной и той же липкой, тягучей, растяжимой материи — чего-то наподобие кошмарно прочной жевательной резинки, которая совершенно не рвется. Ричард Фейнман использовал термин «партоны» для описания частей нуклона, однако закрепились термины «кварки» и «глюоны», которые предложил Мюррей Гелл-Манн. Глюоны — это как раз тот липкий материал, который образует струны и не дает кваркам разлетаться.
Мезоны — это простейшие адроны. Открыто множество разных типов мезонов, но все они имеют одно и то же строение: один кварк и один антикварк, соединенные липкой струной.

Мезон может вибрировать, как пружина, крутиться вокруг своей оси, как чирлидерский жезл, изгибаться и складываться разными способами. Мезоны — это пример открытых струн, то есть струн, имеющих концы. В этом отношении они отличаются от резиновых колец, которые мы будем называть замкнутыми струнами.
Нуклоны состоят из трех кварков, каждый из которых присоединен к струне, а три струны сходятся в центре, как у боласа индейцев гаучо. Они тоже могут крутиться и вибрировать.
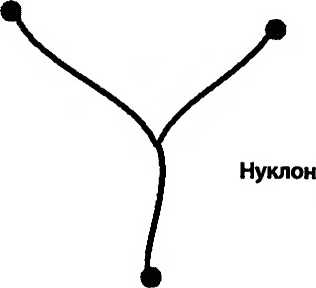
Быстрое вращение и вибрация адрона добавляют струне энергию, растягивают ее и увеличивают ее массу.
Существует еще один тип адронов — семейство «бескварковых» частиц, состоящих только из струн, замкнутых на себя и образующих петлю. Физики называют их глюболами, но для струнного теоретика это просто замкнутые струны.

Не похоже, чтобы кварки состояли из еще меньших частиц. Подобно электронам, они столь малы, что их размеры неизмеримы. Но струны, которые связывают кварки между собой, определенно состоят из других объектов, и эти объекты — не кварки. Липкие частицы, которые соединяются в струны, называются глюонами.
По сути, глюоны — это очень маленькие кусочки струны. Будучи чрезвычайно малыми, они тем не менее имеют два «конца» — положительный и отрицательный, — почти как если бы они были маленькими магнитами.

Математическая теория кварков и глюонов называется квантовой хромодинамикой (КХД). Может показаться, что это название связано с цветной фотографией, а не с элементарными частицами. Но терминология скоро прояснится.
Согласно математическим правилам КХД, глюон не может существовать сам по себе. По математическим законам его положительный и отрицательный концы должны быть присоединены либо к другим глюонам, либо к кваркам: каждый положительный конец должен присоединиться к отрицательному концу другого глюона или к кварку; каждый отрицательный конец должен присоединиться к положительному концу другого глюона или к антикварку; наконец, три положительных или три отрицательных конца могут соединиться вместе. По этим правилам легко можно собрать нуклоны, мезоны и глюболы.
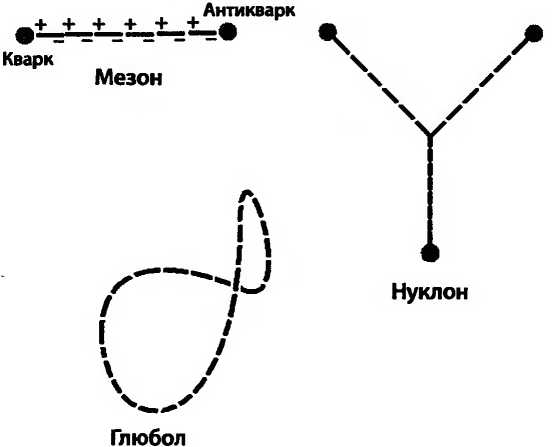
Теперь рассмотрим, что происходит, если кварк в мезоне подвергся воздействию очень большой силы. Такой кварк начинает быстро удаляться от антикварка. Если бы все было так, как с электроном в атоме, то он бы улетел прочь, но здесь случается совсем другое. При удалении кварка от своего партнера между глюонами возникают зазоры, как между молекулами резиновой ленты, когда ее слишком сильно растягивают. Но вместо разрыва глюоны клонируют себя, порождая новые глюоны для заполнения зазоров. Так формируется струна между кварком и антикварком, которая предотвращает убегание кварка. На следующем рисунке показана временная последовательность состояний при такой высокоскоростной попытке убегания кварка от антикварка в мезоне.
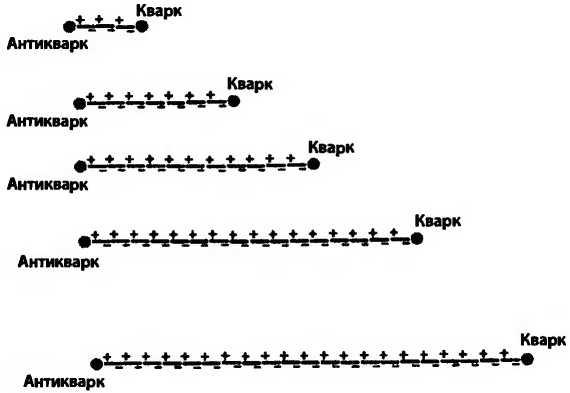
В конце концов кварк исчерпает свою энергию, остановится и вернется обратно к антикварку. То же самое случится и с разогнавшимся кварком в нуклоне.
Струнная теория нуклонов, мезонов и глюболов — это не досужие спекуляции. За прошедшие годы она была исключительно точно подтверждена и рассматривается как часть стандартной теории адронов. Что вызывает путаницу, так это вопрос, следует ли рассматривать струнную теорию как вытекающую из квантовой хромодинамики, иными словами, должны ли струны считаться длинными цепочками долее фундаментальных глюонов или же предпочесть другой способ объяснения: что глюоны — не более чем короткие сегменты струн. Возможно, что оба подхода верны.
Кварки кажутся столь же маленькими и элементарными, как электроны. Они не могут раскручиваться, сжиматься или деформироваться. Но, несмотря на то что в них не видно внутренних частей, они обладают степенью сложности, которая выглядит парадоксальной. Существует много типов кварков с разными электрическими зарядами и массами. Что вызывает эти различия, остается загадкой; внутренние механизмы, лежащие в основе этих различий, слишком малы, чтобы можно было их различить. Поэтому мы называем кварки элементарными, по крайней мере пока, и, как ботаники, даем им разные названия.
Перед Второй мировой войной, когда физикой в основном занимались европейцы, для именования частиц использовали греческий язык. Фотоны, электроны, мезоны, барионы, лептоны и даже адроны происходят из греческого языка. Но потом порывистые, непочтительные и порой глупые американцы взяли верх, и названия упростились. «Кварк» — это бессмысленное слово из романа Джеймса Джойса «Поминки по Финнегану», но с этой литературной высоты все покатилось вниз. Отличия между кварками разных типов стали обозначать совершенно неприемлемым термином аромат. Мы могли бы говорить о шоколадных, клубничных, ванильных, фисташковых, вишневых и мятных кварках, но все оказалось не так. Шесть ароматов кварков: верхний, нижний, странный, очарованный, боттом и топ. В какой-то момент названия «боттом» и «топ» показались слишком рискованными, и довольно быстро они превратились в «прелестный» и «истинный».
Главная цель моего рассказа об ароматах в том, чтобы просто проиллюстрировать, как мало мы знаем о строительных блоках материи и насколько условным может быть применение термина элементарные частицы. Но есть и другое различие, очень существенное для работы КХД. Каждый кварк — верхний, нижний, странный, очарованный, прелестный, истинный — может быть трех цветов: красного, голубого и зеленого. Отсюда и возникает «хромо» в квантовой хромодинамике.
Притормозим на минуту. Естественно, кварки слишком малы, чтобы отражать свет в обычном нашем понимании. Цветные кварки — вещь лишь незначительно менее глупая, чем шоколадные, клубничные или ванильные кварки. Однако людям нужны названия для обозначения вещей; называть кварки красными, зелеными или синими не более смешно, чем называть либералов — синими, а консерваторов — красными. И хотя мы понимаем происхождение цвета кварков не лучше, чем происхождение их аромата, цвет играет намного более важную роль в КХД.
Глюоны, согласно КХД, не имеют аромата, но по отдельности они даже еще более цветные, чем кварки. Каждый глюон имеет положительный и отрицательный полюса, а каждый полюс обладает цветом — красным, зеленым или голубым. Можно сказать, что существует девять типов глюонов (это несколько избыточное упрощение, но по сути корректное).
Почему существует три цвета, а не два, не четыре, не какое-то другое число? Тут нет никакой связи с тем, что цветное зрение опирается на три основных цвета. Как я уже отметил, цветные метки произвольны и не имеют ничего общего с цветами, которые мы видим. На самом деле никто не знает, почему их именно три; это одна из тех загадок, которые указывают, как далеки мы еще от полного понимания элементарных частиц. Однако по тому, как они сочетаются в нуклонах и мезонах, мы знаем, что существует три, и только три цвета кварков.
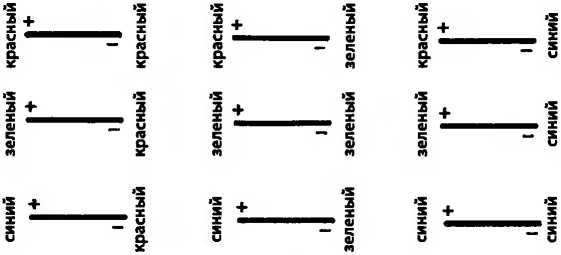
Девять типов глюонов
Тут я должен сделать признание. Несмотря на то что я занимаюсь физикой элементарных частиц более сорока лет, я на самом деле не очень люблю этот раздел физики. Слишком много тут всего намешано: шесть ароматов, три цвета, десятки произвольных числовых постоянных — трудно это назвать примером простоты и элегантности. Почему я продолжаю этим заниматься? Причина (и, я думаю, не только для меня) в том, что сама эта мешанина говорит нам о природе что-то важное. Трудно поверить, что бесконечно малые точечные частицы могут обладать таким числом свойств и такой сложной структурой. На некотором, еще не открытом уровне должен скрываться механизм, поддерживающий все эти так называемые элементарные частицы. Любопытство относительно этого скрытого изрядной сложности механизма и его влияния на фундаментальные законы природы — вот что заставляет меня брести через ужасное болото физики частиц.
Как водится, кварки стали хорошо известны широкой публике. Но если бы меня попросили предсказать, какие из частиц дают нам лучшие подсказки относительно скрытого в глубине механизма, я бы сделал ставку на глюоны. О чем пытаются рассказать нам эти липкие парочки положительных и отрицательных концов?
В главе 4 я объяснял, что в квантовой теории поля есть нечто большее, чем список частиц. Два других «ингредиента» — это пропагаторы, мировые линии, показывающие движение частиц из одной точки пространства-времени в другую, и узлы. Займемся сначала пропагаторами. Поскольку глюоны имеют два полюса, каждый своего цвета, физики часто изображают их мировые линии двойными. Чтобы обозначить конкретный тип глюона, будем подписывать его цвета рядом с отдельными линиями.

Последний «ингредиент» квантовой теории поля — это список узлов. Наиболее важны для нас те узлы, которые описывают распад одного глюона на два. Схема исключительно проста: когда глюон с двумя концами распадается, возникает два новых конца. Согласно математическим правилам КХД, они должны быть одинакового цвета. Рассмотрим два примера. При просмотре снизу вверх видно, что сине-красный глюон распадается на сине-синий и сине-красный; на второй схеме сине-красный глюон распадается на сине-зеленый и зелено-красный.
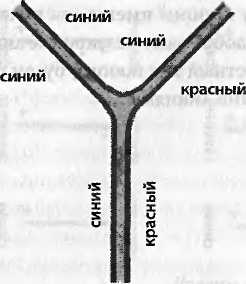
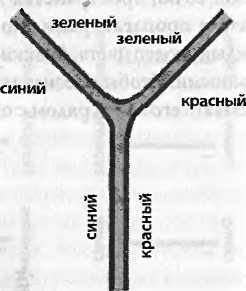
Эти узлы можно перевернуть вниз головой, чтобы показать, как два глюона могут слиться в один.
Хотя все это неочевидно и требует времени для полного понимания, глюоны имеют сильную тягу к слипанию друг с другом и образованию длинных цепочек: положительный конец к отрицательному, красный к красному, синий к синему, зеленый к зеленому. Эти цепочки и есть струны, которые связывают кварки, придавая адронам их струнные свойства.
Струны в фундаменте
Идея эластичных струн вновь всплыла при изучении квантовой гравитации, с той лишь разницей, что они оказались меньше и быстрее примерно на двадцать порядков величины. Эти крошечные, гибкие и невероятно мощные нити энергии называются фундаментальными струнами.
Позвольте мне во избежание недоразумений еще раз повторить, что в современной физике теория струн имеет два совершенно различных приложения. В применении к адронам она используется в масштабах, которые кажутся крошечными по обычным человеческим меркам, но являются гигантскими с точки зрения фундаментальной физики. То, что три типа адронов — нуклоны, мезоны и глюболы — являются струнообразными объектами, которые описываются математикой теории струн, — это признанный факт. Лабораторным экспериментам, лежащим в основе теории адронных струн, уже почти полвека. Струны, которые связывают адроны, а сами состоят из глюонов, называются КХД-струнами. Фундаментальные же струны, связываемые с гравитацией и физикой около-планковского масштаба, как раз и вызвали все волнения, споры, перепалки в блогах и выход в последнее время полемических книг.
Фундаментальные струны могут быть настолько же меньше протона, насколько протон меньше штата Нью-Джерси. Но для них гравитация играет первостепенную роль.
Гравитационные силы во многих отношениях очень похожи на электрические. Формула, описывающая силу взаимодействия между электрически заряженными частицами, называется законом Кулона; формула для сил гравитации — законом всемирного тяготения Ньютона. Обе эти силы — и электрические, и гравитационные — подчиняются закону обратных квадратов. Это значит, что величина силы убывает как квадрат расстояния. Удвоение расстояния между частицами приводит к уменьшению силы в четыре раза; утроение расстояния снижает силу в девять раз; на учетверенном расстоянии сила станет меньше в шестнадцать раз и т. д. Кулоновская сила между двумя частицами пропорциональна произведению их электрических зарядов; ньютоновская сила притяжения пропорциональна произведению их масс. Это сходства, но есть и различия: электрическая сила может быть отталкивающей (между одинаковыми зарядами) или притягивающей (для противоположных зарядов), но гравитация всегда только притягивает.
Одно важное сходство состоит в том, что оба типа сил могут порождать волны. Представьте себе, что происходит с силой, действующей между двумя отдаленными заряженными частицами, когда одна из них неожиданно перемещается, скажем, вдаль от другого заряда. Можно подумать, что сила, действующая на вторую частицу, при смещении первой мгновенно изменится. Но в этой картине кое-что ошибочно. Если сила, действующая на далекую частицу, действительно менялась бы сразу, без задержки, можно было бы использовать этот эффект для отправки мгновенных сообщений в дальние районы космоса. Но мгновенные сообщения нарушают глубочайшие принципы физики. Согласно специальной теории относительности, никакой сигнал не может распространяться быстрее света. Нельзя передать сообщение за меньшее время, чем требуется свету на то, чтобы пройти то же расстояние.
В действительности сила, действующая на дальнюю частицу, не меняется мгновенно при резком движении ближней частицы. Вместо этого от переместившейся частицы начинает распространяться (со скоростью света) возмущение. Только когда оно достигнет дальней частицы, действующая на нее сила изменится. Распространение этого возмущения напоминает волновые колебания. Когда волна наконец приходит, она толкает вторую частицу, заставляя ее вести себя подобно пробке, качающейся на волнах в пруду.
Ситуация аналогична тому, как если бы гигантская рука сдвинула Солнце. Его смещение не ощущалось бы на Земле в течение восьми минут — времени, которое требуется свету, чтобы пройти путь от Солнца. «Послание» распространяется, опять же со скоростью света, в форме колебаний кривизны, или гравитационных волн. Гравитационные волны являются для массы тем же, чем электромагнитные волны — для электрического заряда.
Теперь добавим немного квантовой теории Как мы знаем, энергия колеблющихся электромагнитных волн приходит неделимыми квантами, которые называются фотонами Планк и Эйнштейн имели очень серьезные причины считать, что колебательная энергия может поступать лишь дискретными порциями, и если только мы очень крупно не заблуждаемся, те же аргументы применимы и к гравитационным волнам. Кванты гравитационного поля называются гравитонами.
Здесь я должен сказать, что существование гравитонов, в отличие от фотонов, — это экспериментально не проверенная догадка. Она, как считает большинство физиков, базируется на надежно установленных принципах, но тем нем менее остается гипотезой. Но даже если это так, рассуждения, приводящие к выводу о существовании гравитонов, убедительны для большинства физиков, которые задумывались над этим вопросом.
Сходство между фотонами и гравитонами поднимает интересные вопросы. Электромагнитное излучение объясняется (в квантовой теории поля) фейнмановской диаграммой, в которой заряженная частица — электрон, например, — испускает фотон.
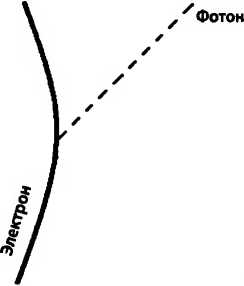
Узел испускания фотона
Естественно ожидать, что гравитационные волны возникают, когда частицы испускают гравитоны. Поскольку в гравитационном взаимодействии участвует всё, то все частицы должны быть способны испускать гравитоны.
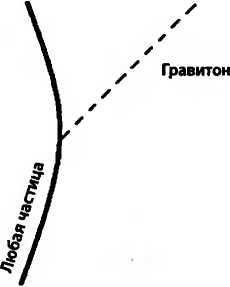
Узел испускания гравитона
Даже гравитоны могут испускать гравитоны.
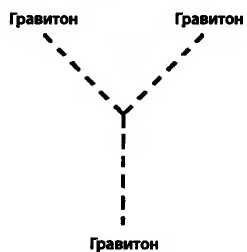
К сожалению, включение гравитонов в фейнмановские диаграммы приводит к математической катастрофе. Почти полвека физики-теоретики пытались придать смысл квантовой теории поля в применении к гравитонам и раз за разом терпели поражение, так что многие из нас пришли к выводу, что это бесполезное дело.
Проблемы с квантовой теорией поля
Одним из ярких эпизодов поездки в Кембридж в 1994году был обед с моим старым другом сэром Роджером Пеироузом. Сэр Роджер как раз только что стал сэром Роджером, и мы с Энн приехали в Оксфорд поздравить его.
Все четверо — мы с Роджером и наши жены — сидели на берегу реки Червелл в приятном открытом ресторанчике, глядя на проплывающих мимо пантеров. Пантинг, если вы не знакомы с этим видом спорта, — это благородный способ катания на лодке с использованием длинного шеста для неспешного отталкивания им от дна. Это буколическое занятие всегда напоминает мне полотно Ренуара «Завтрак лодочников», но в нем есть свои опасности. Когда мимо проплывала лодка с группой поющих студентов, шест у симпатичной девушки, которая с ним управлялась, застрял в иле. Она не желала его отпускать и немало нас позабавила, когда продолжила цепляться за шест, глядя вслед уплывающей лодке.
Тем временем мы вчетвером делили заказанный на всех шоколадный мусс. Дамы уже прикончили свои порции, а мы с Роджеров смеясь над севшей на мель пантершей (она тоже хохотала), еще доедали оставшийся восхитительный темный шоколадный десерт. И тут мое внимание привлекло то, что мы с Роджером, вместо того чтобы брать шоколад полной вилкой, по очереди отрезаем половину от оставшегося куска. Роджер тоже это заметил, и началось соревнование — кто сможет последним разделить оставшийся кусочек.
Греки, напомнил Роджер, интересовались тем, бесконечно ли делима материя или у каждой субстанции есть свои мельчайшие неделимые кусочки — то, что они называли атомами. «Как ты думаешь, а существуют ли атомы шоколада?» — спросил я. Роджер заявил, что не припомнит, является ли шоколад одним из элементов периодической системы. Как бы то ни было, мы наконец доделили мусс до того, что казалось похожим на мельчайший атом шоколада, и, если я не ошибаюсь, он достался Роджеру. Инцидент с пантершей тоже счастливо завершился, когда мимо проплыла следующая лодка.
Проблема с квантовой теорией поля заключается в том, что пространство (и пространство-время) в ней подобны бесконечно делимому шоколадному муссу. Как бы тонко вы его ни нарезали, всегда можно разделить его еще тоньше. Все великие математические загадки имеют дело с бесконечностью. Как представить, что числа идут друг за другом без конца? Но как представить себе, что это не так? Как пространство может быть бесконечно делимым? Но как оно может таковым не быть? Я подозреваю, что бесконечность — главная причина помешательств среди математиков.
Помешанные или нет, математики называют бесконечно делимое пространство континуумом. Проблема с ним в том, что на самых малых расстояниях в нем может происходить ужасающее число событий. Фактически в континууме нет самого малого расстояния — вы можете сгинуть в процессе бесконечного спуска ко все меньшим и меньшим клеткам, и события будут происходить на каждом уровне. Иначе говоря, континуум может содержать бесконечное число битов информации в любом крошечном объеме пространства, сколь бы мал он ни был.
Проблема бесконечно малых особенно неприятна в квантовой механике, где все, что может дрожать, — дрожит, и «все, что не запрещено, обязательно». Даже в пустом пространстве при абсолютном нуле поля, такие как электрическое и магнитное, флуктуируют.
Эти флуктуации происходят во всех масштабах — от самых больших волн с длиной в миллиарды световых лет до волн размером не больше математической точки. Эта дрожь квантовых полей позволяет хранить неограниченное количество информации в любом крошечном объеме. И это рецепт математической катастрофы.
Потенциально бесконечное число битов в каждом крошечном объеме пространства проявляется на фейнмановских диаграммах как бесконечный переход ко все меньшим и меньшим субдиаграммам. Начнем с простой идеи пропагатора, изображающего электрон, движущийся из одной пространственно-временной точки в другую. Он начинается и заканчивается одним электроном.

Для электрона есть и другие способы попасть из точки а в точку b — например, жонглируя по пути фотонами.

Очевидно, что число таких возможностей бесконечно, а согласно фейнмановским правилам, все они должны быть просуммированы, чтобы определить вероятность. Каждую диаграмму можно украсить дополнительными структурами. Каждый пропагатор и узел можно заменить более сложной историей, включающей диаграммы внутри диаграмм внутри диаграмм, пока они не станут неразличимо мелкими. Но, пользуясь мощной лупой, можно добавлять еще более мелкие структуры, и так до бесконечности.
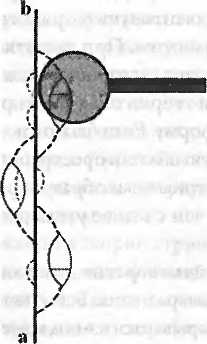

Возможность бесконечно добавлять на фейнмановские диаграммы все более мелкие структуры — одно из тревожных следствий континуальности пространства-времени в квантовой теории поля: количество шоколадного мусса всегда можно уменьшить.
С учетом всего этого — неудивительно, что квантовая теория поля математически опасный предмет. Непросто добиться, чтобы все флуктуации в бесконечно большом числе бесконечно малых ячеек пространства собрались в целостную вселенную. В действительности квантовая теория поля по большей части идет вразнос и дает бессмыслицу. Даже Стандартная модель элементарных частиц может при окончательном анализе не оказаться математически корректной.
Но ничто не сравнится с трудностями, возникающими, когда пробуешь построить квантовую теорию гравитации. Напомню, гравитация — это геометрия. При попытках совместить общую теорию относительности с квантовой механикой оказывается, что по правилам квантовой теории поля само пространство-время постоянно меняет свою форму. Если бы можно было рассмотреть под увеличением крошечную область пространства, мы увидели бы, что оно бешено дрожит, изгибаясь и образуя крошечные кочки и узлы кривизны. Более того, чем сильнее увеличение, тем неистовее становятся эти флуктуации.
Гипотетические фейнмановские диаграммы, включающие гравитоны, отражают эти извращения. Бесконечное число все меньших и меньших диаграмм вырывается из-под контроля. Каждая попытка придать смысл квантовой теории поля для гравитации приводила к одному и тому же результату: в самых малых масштабах происходит слишком много всего. Применение обычных методов квантовой теории поля к гравитации ведет к математическому фиаско.
У физиков есть способ обойти катастрофу, связанную с бесконечной делимостью пространства: они притворяются, будто пространство, подобно шоколадному муссу, не является истинным континуумом. Предполагается, что, дойдя в делении пространства до определенной точки, вы обнаружите у него неделимые крупицы, которые уже нельзя больше раздробить. Иными словами, они прекращают рисование фейнмановских диаграмм, когда их подструктуры становятся слишком маленькими. Это ограничение по малости величины называется перенормировкой. По сути, перенормировка — не что иное, как разбиение пространства на неделимые вокселы, вмещающие не более одного бита.
Перенормировка кажется уходом от проблемы, но для нее есть одно оправдание. Физики долго рассуждали о том, что планковская длина является предельно малым атомом пространства. Фейнмановские диаграммы, даже включающие гравитоны, сохраняют четкий смысл, если только прекратить добавлять к ним структуры меньше планковского размера или около того. Поэтому почти все ожидали, что пространство на планковском масштабе имеет неделимую, гранулярную, вокселизированную структуру.
Но это было до открытия голографического принципа. Как мы увидели в главе 18, замена непрерывного пространства массивом вокселов, имеющих конечный, планковский размер, — это ошибочная идея. Вокселизация пространства значительно завышает число вариантов заполнения его областей. Это привело бы Птолемея к ошибочному выводу относительно числа битов, которые могут храниться в его библиотеке, а теоретических физиков — к неверному представлению о количестве информации, которая может содержаться в области пространства.
Почти с самого появления теории струн признавалось, что она решает загадку бесконечно малых фейнмановских диаграмм. Отчасти она достигает этого, избавляясь от идеи бесконечно малых частиц. Но вплоть до появления голографического принципа недооценивалось, насколько радикально теория струн отличается от перенормировочной или вокселизированной версии квантовой теории поля. Замечательный факт состоит в том, что теория струн — это принципиально голографическая теория, описывающая пикселизированный мир.
Современная теория струн, как и ее более ранние воплощения, имеет дело с открытыми и замкнутыми струнами. В большинстве, хотя и не во всех, версий теории фотон — это открытая струна, подобная мезону, но только значительно меньше. Во всех версиях гравитон — это замкнутая струна, больше всего напоминающая миниатюрный глюбол. Может ли быть так, что в каком-то неожиданном глубоком смысле эти два типа струн — фундаментальные и КХД-струны — окажутся одними и теми же объектами? С учетом различия в их размерах это кажется маловероятным, однако струнные теоретики стали подозревать, что это огромное различие в масштабах может вводить в заблуждение. В главе 23 мы увидим, что в теории струн есть определенное единство, но пока мы будем говорить о двух разных теориях струн для разных явлений.
Струна — это гибкий объект, длина которого много больше толщины: шнурок для ботинок или рыболовная леска — это струны. В физике слово «струна» также подразумевает эластичность: струны могут растягиваться и сжиматься, подобно жгуту эспандера или резиновой ленте. КХД-струны очень прочные — к концу мезона можно подвесить большой грузовик, но фундаментальные струны еще прочнее. На самом деле, невзирая на ничтожную толщину, фундаментальные струны так невероятно прочны, что в мире обычной материи их не с чем сравнить. Число грузовиков, которое могла бы выдержать фундаментальная струна, составляет около 1040. Из-за этого колоссального натяжения чрезвычайно трудно растянуть фундаментальную струну до сколько-нибудь заметных размеров. Поэтому типичные размеры фундаментальных струн должны быть ненамного больше планковской длины.
Для струн, с которыми мы сталкиваемся в повседневной жизни, — жгутов для эспандера, резиновых лент и растянутых жевательных резинок — квантовая механика особой роли не играет, но КХД-струны и фундаментальные струны — это существенным образом квантово-механические объекты. Среди прочего это означает, что энергия может добавляться им лишь дискретными, неделимыми порциями. Переход от одного значения энергии к другому может быть выполнен только «квантовым скачком» вверх по лестнице энергетических уровней.
Нижний конец энергетической лестницы называется нулевым состоянием. Добавление одной единицы энергии переводит в первое возбужденное состояние. Следующий энергетический шаг дает второе возбужденное состояние и так далее шаг за шагом. Обычные элементарные частицы, такие как электроны и фотоны, находятся внизу лестницы. Если они вообще вибрируют, это лишь квантовые нулевые колебания. Но если теория струн верна, то их можно заставить вращаться и колебаться со все большей энергией (а значит, и массой).
Гитарную струну можно возбудить, щипнув медиатором, но, как вы понимаете, гитарный медиатор великоват для того, чтобы возбудить электрон. Простейший способ состоит в том, чтобы ударить электрон другой частицей. В результате мы используем одни частицы в качестве «медиаторов», чтобы «щипать» другие. Если столкновение достаточно сильное, оно заставит обе струны вибрировать в возбужденных состояниях. Естественно задать вопрос: «Почему бы физикам-экспериментаторам не возбудить электроны и протоны на ускорителях, сняв тем самым, раз и навсегда, вопрос о том, являются ли частицы вибрирующими струнами?» Проблема в высоте ступеньки — она слишком велика. Энергия, необходимая для того, чтобы закрутить или заставить вибрировать адрон, — довольно умеренная по стандартам современной физики элементарных частиц, но энергия, требуемая для возбуждения фундаментальной струны, чрезмерно велика. Добавление электрону одной порции энергии увеличило бы его массу почти на планковскую величину. Еще хуже то, что эту энергию надо сконцентрировать в невероятно малом объеме пространства. Грубо говоря, потребовалось бы затолкать массу миллиарда миллиардов протонов в область размером в миллиард миллиардов раз меньше самого протона. Ни один из построенных ускорителей даже близко не подходит для такой задачи. Подобное никогда не делалось и, вероятно, никогда не будет сделано.
Сильно возбужденные струны в среднем больше тех, что находятся в нулевом состоянии; дополнительная энергия растягивает их, увеличивая их длину. Если суметь вкачать в струну достаточную энергию, она растянется и станет похожа на большой, безумно дрожащий, запутанный клубок шерсти И тут нет предела; при наличии достаточной энергии струну можно растянуть до любого размера.
Есть только один способ, которым сильно возбужденные струны могут быть получены в природе, раз уж их не получить в лаборатории. Как мы увидим в главе 21, черные дыры — даже те гиганты, что находятся в центрах галактик, — это колоссальные запутанные «струны-монстры».
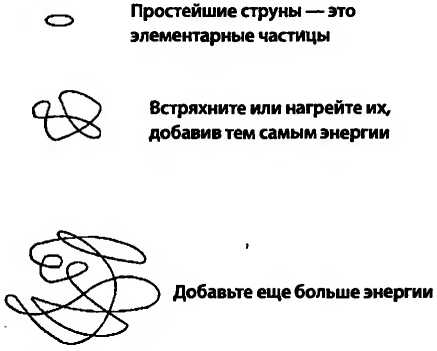
Существует еще одно важное и удивительное следствие квантовой механики, слишком тонкое и технически сложное, чтобы объяснять его здесь. Пространство, каким мы его обычно воспринимаем, трехмерно. Существует много терминов для описания этих трех измерений, например долгота, широта и возвышение или длина, ширина и высота. Математики и физики часто описывают размерности, используя три оси, обозначенные x,yw.z.
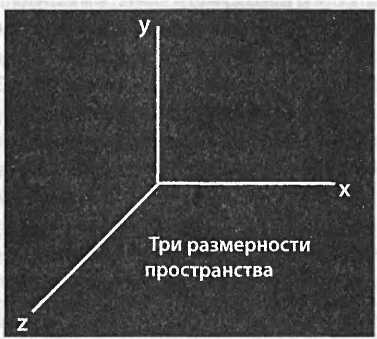
Однако фундаментальным струнам недостаточно для движения только трех измерений. Я имею в виду, что тонкая математика теории струн становится ненадежной, пока к пространству не добавляются дополнительные измерения. Струнные теоретики много лет назад обнаружили, что математическая согласованность их уравнений нарушается, если не ввести шесть дополнительных измерений пространства. Мне всегда казалось, что если понимаешь что-то достаточно хорошо, то должна быть возможность объяснить это неформально. Но потребность теории струн в шести дополнительных измерениях так и не поддается простому объяснению, хотя прошло уже тридцать пять лет. Боюсь, тут я вынужден буду прибегнуть к методу негодяев и сказать: «Можно показать, что…»
Я бы очень удивился, встретив кого-то, способного представить себе четыре или пять измерений, не говоря уже о девяти. Мне это удается не лучше, чем вам, но я могу добавить шесть букв алфавита — r, s, t, и, v, w — к обычным х, у и z, а затем терзать эти символы методами алгебры и анализа. При девяти измерениях, доступных для движения, «можно показать, что» теория струн становится математически согласованной.
Теперь вы можете спросить: если теория струн требует девяти измерений, а наблюдаемое пространство имеет только три, не является ли это прямым доказательством того, что теория струн неверна? Но не все так просто. Многие знаменитые физики, включая Эйнштейна, Вольфганга Паули, Феликса Клейна, Стивена Вайнберга, Мюррея Гелл-Манна и Стивена Хокинга (никто из них не является струнным теоретиком), серьезно рассматривали возможность того, что пространство имеет более трех измерений. Очевидно, они не галлюцинировали, значит, должен быть какой-то способ скрыть существование дополнительных размерностей. Характерные словечки, используемые для обозначения сокрытия дополнительных измерений, — «свертка» и «компактификация». Струнные теоретики сворачивают шесть дополнительных измерений посредством процесса, называемого компактификацией. Идея состоит в том, что дополнительные измерения пространства могут быть скручены в очень маленькие узлы, так что мы, огромные создания, слишком велики, чтобы в них перемещаться или даже заметить их.
Представление о том, что одно или более измерений можно скрутить в крошечную геометрическую форму, слишком маленькую, чтобы ее заметить, — это общее место современной физики высоких энергий. Некоторые люди думают, что дополнительные измерения — это слишком умозрительная идея, «научная фантастика с уравнениями», как сказал один остряк. Но это недопонимание, основанное на невежестве. Все современные теории элементарных частиц используют своего рода дополнительные размерности для обеспечения недостающих механизмов, которые делают частицы сложными.
Струнные теоретики не изобрели концепцию дополнительных измерений, а использовали ее особым творческим способом. Хотя теория струн требует шести дополнительных измерений, общее представление можно получить, добавив к пространству всего одно новое измерение. Давайте исследуем идею дополнительных измерений в этой ее простейшей ипостаси. Начав с мира, имеющего только одно пространственное измерение, — назовем его Лайнландией, — мы добавим одно дополнительное свернутое измерение. Для указания точки в Лайнландии достаточно всего одной координаты; обитатели называют ее X.
Чтобы Лайнландия стала интереснее, нам надо добавить в нее объекты, так что создадим частицы, которые движутся вдоль линии.

Думайте о них как о крошечных бусинах, которые сцепляются друг с другом, образуя одномерные атомы, молекулы и, возможно, даже живых существ. (Я сильно сомневаюсь, что жизнь может существовать в мире с одним измерением, но давайте пока подержим эти сомнения при себе.) Считайте и линию, и бусины бесконечно тонкими, так что они не высовываются в другие измерения. А лучше даже попытаться представить себе линию с бусинами вообще без других измерений.
Сообразительный человек придумает много альтернативных версий Лайнландии. Все бусины могут быть одинаковыми, или, в более интересном мире, может существовать несколько разных типов бусин. Чтобы различать эти типы, пометим их цветами — красным, синим, зеленым и т. д. Я могу представить себе бесчисленно множество возможностей: красные бусины притягивают синие, но отталкивают зеленые. Черные бусины очень тяжелые, а белые — безмассовые и движутся по Лайнландии со скоростью света. Можно даже позволить бусинам быть квантово-механическими, цвет каждой отдельной бусины может быть неопределенным.
Жизнь в одном-единственном измерении очень стесненная. Имея свободу двигаться только вдоль одной линии, лайнландцы непременно будут сталкиваться друг с другом. Смогут ли они общаться? Легко: для отправки сообщений они могут перебрасываться бусинами, находящимися у их концов. Однако их социальная жизнь очень уныла: каждое существо имеет лишь двоих знакомых — одного справа и одного слева. Нужно по меньшей мере два измерения, чтобы сформировать социальный круг.
Но внешность обманчива. Когда лайнландцы смотрят в очень сильный микроскоп, они начинают обнаруживать, что их мир в действительности двумерный. Они видят не идеальную математическую линию нулевой толщины, а скорее поверхность цилиндра. В обычных обстоятельствах окружность этого цилиндра слишком мала, чтобы лайнландцы могли ее обнаружить, но под микроскопом удалось открыть куда более мелкие объекты, меньше даже, чем лайнландские атомы. Эти объекты столь малы, что могут двигаться в двух измерениях.

Подобно своим братьям-великанам, эти лайнландские карлики могут перемещаться вдоль цилиндра, но они достаточно малы, чтобы обходить по его окружности. Они способны даже двигаться одновременно по обоим направлениям, накручивая спиральные витки вокруг цилиндра. И — о, радость! — они могут даже обходить друг друга без столкновений. Вполне резонно они утверждают, что живут в двумерном пространстве, но с одной особенностью: если двигаться по прямой линии в дополнительном измерении, то скоро вернешься в исходную точку.
Лайнландцам понадобилось название для нового направления, и они обозначили его Y. В отличие от Х, вдоль Y нельзя далеко уйти, не вернувшись в исходную точку. Лайнландские математики говорят, что направление Y компактифицировано.
Цилиндр, изображенный выше, получается при добавлении дополнительного свернутого измерения к исходному одномерному миру. Добавление шести дополнительных измерений к миру, в котором уже есть три обычных, выходит далеко за пределы способностей человеческого мозга к визуализации. Физиков и математиков отличает от остальных людей не то, что они мутанты, способные представить себе любое число измерений, а скорее то, что они прошли тяжелую математическую переподготовку, опять же, перепрошивающую сознание, — чтобы научиться «видеть» дополнительные измерения.
Единственное дополнительное измерение не обеспечивает достаточного разнообразия возможностей. Перемещение в свернутом направлении будет подобно движению по кругу без осознания этого. Но уже два дополнительных измерения открывают бесконечное множество новых возможностей. Два измерения могут образовать сферу.

тор (поверхность бублика),

бублик с двумя или тремя дырками,

или даже причудливое пространство, называемое бутылкой Клейна.

Изображение двух дополнительных измерений не составляет больших проблем (мы только что сделали это), но с ростом числа измерений визуализировать их становится все труднее и труднее. К тому моменту когда мы достигнем шести дополнительных измерений, необходимых для теории струн, визуализация без обращения к математике становится безнадежным делом. Особые геометрические пространства, которые струнные теоретики используют для компактификации шести дополнительных измерений, называются многообразиями Калаби — Яу. Их насчитываются миллионы, и среди них нет двух одинаковых. Многообразия Калаби — Яу исключительно сложны, с сотнями шестимерных дырок от бубликов и прочими невообразимыми кренделями. Тем не менее математики создают их изображения, нарезая на слои меньшей размерности, подобно диаграммам вложения. Вот изображение двумерного среза типичного пространства Калаби — Яу.
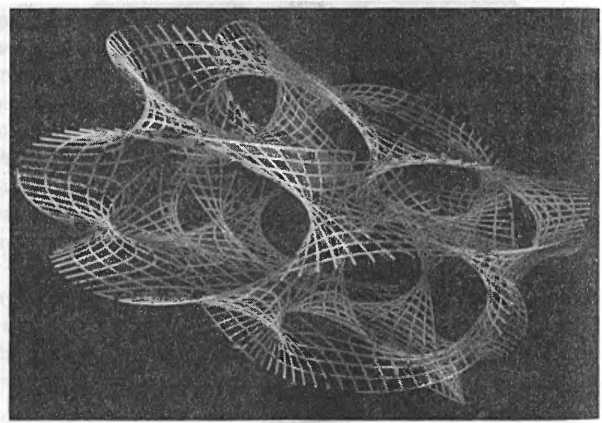
Я попробую дать вам некоторое представление о том, на что похоже обычное пространство, когда к каждой его точке добавлено шестимерное многообразие Калаби — Яу. Сначала посмотрите на обычные измерения, в которых могут двигаться такие большие объекты, как люди. (Я нарисовал его двумерным, но вы уже должны научиться достраивать третье измерение в воображении.)

В каждой точке трехмерного пространства имеется также шесть других свернутых измерений, в которых могут перемещаться очень маленькие объекты. По необходимости я рисую пространства Калаби — Яу отдельно друг от друга, но вы должны представлять себе их в каждой точке обычного пространства.

Теперь вернемся к струнам. Обычный жгут от эспандера можно растягивать в разных направлениях, например вдоль оси восток — запад, или север — юг, или верх — низ. Его можно растягивать под разными углами, скажем, на север-северо-запад с 10-градусным наклоном к горизонту. Но если есть дополнительные измерения, число возможностей многократно возрастает. В частности, струны Могут растягиваться вдоль свернутых измерений. Замкнутая струна Может опоясывать пространство Калаби — Яу один или несколько Раз, но при этом вовсе не быть растянутой в обычных пространственных направлениях.

Позвольте мне еще немного усложнить ситуацию. Струна может опоясывать свернутое пространство и в то же самое время извиваться, подобно змее, так что изгибы прокатываются по струне.

Чтобы натянуть струну вокруг свернутого измерения и заставить ее вибрировать, требуется энергия, так что частицы, описываемые такими струнами, будут тяжелее обычных.
Силы
Наша Вселенная — это мир не только пространства, времени и частиц, но также и сил. Электрические силы, действующие между заряженными частицами, могут перемещать кусочки бумаги и пылинки (скажем, за счет статического электричества), но более важно, что эти силы удерживают электроны на их орбитах вокруг атомных ядер. Гравитационные силы, действующие между Землей и Солнцем, удерживают на орбите Землю.
Все силы в конечном счете связаны с микроскопическими силами, действующими между отдельными частицами. Но откуда берутся эти межчастичные силы? Для Ньютона универсальная силапритяжения, действующая между массами, была просто физическим фактом — в действительности он смог ее только описать, но не объяснить. Однако в течение девятнадцатого и двадцатого столетий такие физики, как Майкл Фарадей, Джеймс Клерк Максвелл, Альберт Эйнштейн и Ричард Фейнман, сделали блестящие открытия, объяснявшие силы через стоящие за ними более фундаментальные концепции.
Согласно Фарадею и Максвеллу, электрические заряды притягиваются и отталкиваются не непосредственно; в пространстве между зарядами существует посредник, передающий взаимодействие. Представьте себе «Слинки» — эту ленивую игрушечную пружинку, — натянутую между двумя разнесенными на некоторое расстояние шарами.

Каждый из шаров подвергается воздействию силы только со стороны присоединенного к нему конца «Слинки». Затем каждый фрагмент «Слинки» воздействует на своих соседей. Сила передается по «Слинки», пока не передаст натяжение к объекту на другом конце. Может казаться, что два объекта притягиваются друг к другу, но это иллюзия, созданная посредничающей между ними «Слинки».
Когда доходит до электрически заряженных частиц, посредничающие агенты — это заполняющие пространство между ними электрическое и магнитное поля. Хотя они невидимы, эти поля совершенно реальны: это непрерывные невидимые возмущения пространства, которые переносят взаимодействия между зарядами.
Эйнштейн в своей теории гравитации пошел еще глубже. Массы искривляют геометрию пространства-времени в своей окрестности и благодаря этому искажают траектории других масс. Искажения геометрии тоже можно рассматривать как поля.

Электрическое поле положительного заряда

Магнитное поле стержневого магнита
Могло показаться, что на этом все кончится. Так и было, пока не появился Ричард Фейнман с квантовой теорией сил, которая на первый взгляд была совершенно не похожа на теории поля Фарадея — Максвелла и Эйнштейна. Его теория начинается с представления о том, что электрически заряженные частицы могут испускать (бросать) и поглощать (ловить) фотоны. В этой идее еще не было ничего странного; давно уже было понято, что электроны испускают рентгеновские лучи, когда внезапно останавливаются у препятствия в рентгеновской трубке. Обратный процесс поглощения был описан Эйнштейном в его статье, где он впервые ввел идею световых квантов.
Фейнман изображал заряженные частицы в виде жонглеров фотонами, постоянно испускающими и поглощающими их и создающими в пространстве, окружающем заряд, огромное число фотонов. Отдельный покоящийся электрон — это идеальный жонглер, никогда не теряющий то, что подбросил. Но, как и в случае с жонглером-человеком в железнодорожном вагоне, неожиданное ускорение может все нарушить. Заряд может сместиться со своей позиции, из-за чего окажется не в том месте, чтобы поглотить фотон. Этот упущенный фотон улетает прочь и становится частью излучаемого света.
Вернемся в железнодорожный вагон, где в поезд вместе с жонглером садится его партнер, и они вдвоем решают попрактиковаться в командной жонглерской работе. В основном каждый жонглер ловит свои собственные броски, но при сближении время от времени каждый из них может ловить шары, брошенные другим. То же самое происходит, когда сближаются два электрических заряда. Окружающие их облака фотонов смешиваются, и один заряд может поглощать фотоны, испущенные другим. Этот процесс называется обменом фотонами.
В результате обмена фотонами возникают силы, с которыми заряды действуют друг на друга. На сложный вопрос о том, будет ли сила притягивающей или отталкивающей, можно ответить лишь с учетом всех тонкостей квантовой механики. Достаточно сказать, что, когда Фейнман выполнял свои вычисления, он обнаружил то же, что Фарадей и Максвелл: одинаковые заряды отталкиваются, а противоположные — притягиваются.
Интересно сравнить жонглерские навыки электронов и жонглеров-людей. Человек, по-видимому, может бросать и ловить предметы несколько раз в секунду, однако электрон испускает и поглощает фотоны примерно 1019 раз в секунду.
По теории Фейнмана, жонглерами являются все материальные частицы, а не только электрические заряды. Любая форма материи испускает и поглощает гравитоны — кванты гравитационного поля. Земля и Солнце окружены облаками гравитонов, которые перемешиваются и участвуют в обмене. А в результате гравитационная сила удерживает Землю на орбите.
Сколь же часто отдельный электрон испускает гравитон? Ответ довольно неожиданный: совсем нечасто. В среднем время, необходимое электрону, чтобы испустить гравитон, превышает весь возраст Вселенной. Вот почему, по фейнмановской теории, гравитационное взаимодействие между элементарными частицами настолько слабее электрического.
Так какая же теория верна: полевая Фарадея — Максвелла — Эйнштейна или фейнмановская теория частиц-жонглеров? Они кажутся слишком разными, чтобы быть правильными одновременно.
И тем не менее обе они верны. Все дело в квантовой дополнительности между волнами и частицами, о которой я рассказывал в главе 4. Волны — это полевая концепция: световые волны — это не что иное, как быстрые колебания электромагнитных полей. Но свет — это частицы, фотоны. Так что картины с фейнмановскими частицами и максвелловскими полями — просто еще один пример квантовой дополнительности. Квантовое поле, порожденное облаком частиц, которыми жонглируют, называется конденсатом.
Струнная шутка
Позвольте мне рассказать свежий анекдот, который стал популярен среди струнных теоретиков.
Пара струн заходит в бар и заказывают по пиву. Бармен говорит одной из них: «Давно тебя не видел. Как дела?» Затем поворачивается к другой струне и спрашивает: «Ты ведь здесь впервые? Ты так же замкнут, как и твоя подруга?» И получает в ответ: «Нет, я чертов узел».
М-да… А чего вы ждали от струнного теоретика?
Шутка на этом заканчивается, но история продолжается. Бармен чувствует легкое опьянение. Возможно, это результат лишней рюмки, тайно принятой за стойкой, или, быть может, мерцание квантовых флуктуаций зашедшей пары немного вскружило ему голову. Но нет, это что-то большее, чем стандартная дрожь; струны, похоже, движутся очень странно, как будто какая-то скрытая сила тянет и соединяет их между собой. Каждый раз, когда одна струна делает неожиданное движение, мгновением позже другая срывается со своего сиденья, и наоборот. Но внешне их, кажется, ничто не соединяет.
Удивленный этим загадочным поведением бармен внимательно всматривается в пространство между ними, пытаясь разобраться. Поначалу он может разглядеть только слабое мерцание, дрожащее искажение геометрии, но где-то через минуту он замечает, что маленькие кусочки струн постоянно отрываются от тел двух клиентов, формируя между ними конденсат. Именно этот конденсат притягивает их и заставляет резко двигаться.
Струны испускают и поглощают другие струны. Рассмотрим случай замкнутых струн. В дополнение к обычной дрожи нулевых колебаний квантовая струна может разделиться на две струны. Я опишу этот процесс в главе 21, а пока нам хватит простой картинки, иллюстрирующей эту идею. Вот изображение замкнутой струны.

Струна извивается и дрожит, пока на ней не появляется небольшое выступающее ушко.
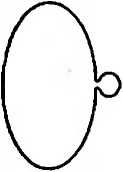
Теперь струна готова разделиться и излучить свой небольшой кусочек.

Противоположное тоже возможно: маленькая струна, встретив Другую, большую струну, может быть поглощена в ходе обратного процесса.
Небольшие замкнутые струнные кольца — это гравитоны, роящиеся вокруг более крупных струн и образующие конденсат, который очень напоминает по своим проявлениям гравитационное поле. Гравитоны — кванты гравитационного поля — похожи по строению на глюболы ядерной физики, но в 1019 раз меньше. Интересно, как все это связано (если связано) с ядерной физикой?
Некоторых специалистов из других областей физики раздражает энтузиазм струнных теоретиков, которые уверяют: «Прекрасная, элегантная, непротиворечивая, устойчивая математика теории струн приводит к удивительным, невероятным, фантастическим фактам, касающимся сил гравитации, а значит, она должна быть верной». Однако для скептически настроенного стороннего наблюдателя подобные славословия, даже если они оправданы, никак не повышают убедительность аргументов. Если теория струн дает верную картину реальности, то подтверждать это надо убедительными экспериментальными предсказаниями и эмпирическими проверками, а не восхвалениями. Скептики правы, но правы и струнные теоретики. Настоящая проблема заключается в чрезвычайной трудности экспериментирования с объектами размером, в миллиард миллиардов раз меньшим протона. Но будет теория струн в итоге подтверждена экспериментальными данными или нет, в настоящее время это надежная математическая лаборатория, в которой проверяются различные идеи относительно того, как гравитация согласуется с квантовой механикой.
Поскольку в теории струн появляется гравитация, можно ожидать, что при сближении достаточно массивных струн должна образовываться черная дыра. Таким образом, теория струн — это концепция, в рамках которой можно исследовать хокинговский парадокс. Если Хокинг прав в том, что черные дыры неизбежно приводят к потере информации, тогда математика теории струн должна это подтвердить. Если Хокинг ошибается, теория струн должна показать, как может информация выходить из черной дыры.
В начале 1990-х годов мы с Герардом 'т Хоофтом (если я правильно помню) дважды встречались в Стэнфорде и один раз в Утрехте, и в этот период 'т Хоофт в целом не доверял теории струн, несмотря на то что сам написал одну из основополагающих статей, объясняющих взаимосвязь теории струн и квантовой теории поля. Я никогда точно не понимал, что именно ему не нравилось, но мне кажется, что отчасти это связано с совершенно безальтернативным доминированием струнных теоретиков в истеблишменте американской теоретической физики начиная с 1985 года. Вечно идущий против общего тренда 'т Хоофт верил (как и я) в силу разнообразия. Чем большим числом разных способов вы подходите к вопросу, чем больше разных стилей мышления применяется, тем выше шансы решить по-настоящему сложные научные проблемы.
Но у скептицизма Герарда были и другие причины помимо того, что он не переваривал захвата физики слишком узкой группировкой. Насколько я знаю, он признавал ценность теории струн, но был категорически против утверждений о том, что она является «окончательной теорией». Теория струн была открыта случайно, и ее развитие шло рывками. У нас никогда не было исчерпывающего набора принципов или небольшого набора основных уравнений. Даже сегодня она состоит из паутины взаимосвязанных математических фактов, которые удивительно хорошо соответствуют друг другу, но эти факты не складываются в некий компактный набор принципов, как в ньютоновской теории гравитации или в квантовой механике. Вместо этого имеется сеть элементов, которые хорошо подогнаны друг к другу, как очень сложно нарезанный пазл, общая картина которого просматривается лишь в туманной перспективе. Напомню высказывание 'т Хоофта, которое я приводил в начале главы: «Представьте, что я даю вам кресло, поясняя, что ножек у него пока нет, а сиденье, спинка и подлокотники, возможно, скоро будут доставлены; что бы я вам ни вручил, могу ли я называть это креслом?»
Теория струн действительно пока не является вполне сложившейся системой, но на сегодня это безоговорочно лучший математический ориентир на пути к окончательными принципам квантовой гравитации. И я должен добавить, что она оказалась самым мощным оружием в Битве при черной дыре, особенно в деле подтверждения ожиданий самого Герарда.
В следующих трех главах мы увидим, как теория струн помогла объяснить и подтвердить дополнительность черных дыр, происхождение их энтропии, а также голографический принцип.

