Книга: Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.
Назад: Часть первая Теорема о распределении простых чисел
Дальше: Глава 2. Почва и всходы
Глава 1. Карточный фокус
I.
Как и многие другие представления, это начинается с колоды карт.
Возьмем обычную колоду из 52 карт; положим ее на стол, подровняв со всех сторон. А теперь сдвинем самую верхнюю карту колоды, не пошевелив при этом ни одну из остальных карт. Насколько можно сдвинуть верхнюю карту, чтобы она еще не упала?
Ответ понятен: на половину длины карты, что мы и видим на рисунке 1.1. Если подвинуть ее так, чтобы на весу оказалось более половины карты, она упадет. Точка опрокидывания находится в центре тяжести карты, т.е. на середине ее длины.

Рисунок 1.1.
Теперь сделаем кое-что еще. Пусть верхняя карта так и лежит, сдвинутая на половину своей длины — т.е. с максимальным нависанием, — а мы начнем осторожно сдвигать следующую карту. Насколько в сумме могут нависать две верхние карты?
Фокус состоит в том, что эти две карты надо рассматривать как единое целое. Где у этого целого находится центр тяжести? Ясно, что посередине общей длины — длины в полторы карты. Значит, центр тяжести расположен на расстоянии в три четверти длины карты от выступающего края верхней карты (см. рисунок 1.2). Суммарное нависание, следовательно, равно трем четвертям длины карты. Заметим, что верхняя карта по-прежнему свисает со второй на половину своей длины. Но две верхние карты мы сдвигали как единое целое.

Рисунок 1.2.
Если теперь начать двигать третью карту и посмотреть, насколько можно увеличить нависание, окажется, что ее можно сдвинуть на одну шестую длины карты. Как и ранее, надо воспринимать три верхние карты как единое целое. Центр тяжести тогда расположен на расстоянии в одну шестую длины карты от выдвинутого края третьей карты (см. рисунок 1.3).

Рисунок 1.3.
За край у нас выдвинута одна шестая третьей карты, одна шестая плюс одна четверть второй карты, а также одна шестая плюс одна четверть плюс одна вторая верхней карты, что в сумме дает полторы карты:
1/6 + (1/6 + 1/4) + (1/6 + 1/4 + 1/2) = 11/2.
Это половина от длины трех карт; вторая половина находится за точкой опрокидывания. На рисунке 1.4 изображено, что у нас получилось после максимально возможного сдвига третьей карты.

Рисунок 1.4.
Полное нависание теперь составляет одну вторую (за счет верхней карты) плюс одна четверть (за счет второй карты) плюс одна шестая (за счет третьей). Всего — одиннадцать двенадцатых длины карты. Потрясающе!
Можно ли добиться нависания, превышающего длину одной карты? Да, можно. Прямо следующая карта — четвертая сверху — при осторожном сдвигании добавит к нависанию одну восьмую длины карты. Я не буду проделывать все эти арифметические выкладки — или поверьте мне, или сделайте их сами, подобно тому как мы это только что сделали для трех первых карт. Вот чему равно полное нависание с четырьмя картами: одна вторая плюс одна четверть плюс одна шестая плюс одна восьмая — все вместе одна и одна двадцать четвертая длины карты (см. рисунок 1.5).

Рисунок 1.5.
Если продолжать действовать в том же духе и целиком использовать всю колоду, то за счет пятидесяти одной карты накопится нависание, равное
1/2 + 1/4 + 1/6 + 1/8 + 1/10 + 1/12 + 1/14 + 1/16 + … + 1/102
(самую нижнюю карту сдвигать бессмысленно). Такая сумма на самую толику меньше, чем 2,25940659073334. Таким образом, мы добились полного нависания более чем в две с четвертью длины! (Рис. 1.6.)

Рисунок 1.6.
Я был студентом, когда узнал про это. Дело было в летние каникулы, и я занимался подготовкой к следующему семестру, пытаясь несколько опередить программу. Свой вклад в оплату обучения я вносил, нанимаясь на время каникул рабочим на стройки — в Англии в те времена профсоюзы не сильно контролировали этот сектор. На следующий день после того, как я узнал про фокус с картами, мне предстояло в одиночку прибраться во внутренней части строящегося здания, где пачками хранились сотни больших квадратных потолочных панелей. Часа два я с забавлялся со стопкой из 52 панелей, пытаясь добиться нависания в две с четвертью панели. Проходивший мимо прораб застал меня глубоко погруженным в созерцание гигантской колышущейся башни, составленной из потолочных панелей, и он, я думаю, утвердился в своих худших подозрениях относительно целесообразности найма студентов.
II.
Есть одна вещь, которую очень любят делать математики и которая оказывается очень плодотворной, — это экстраполировать, т.е. брать конкретную задачу и распространять ее выводы на более широкую область.
В нашей конкретной задаче у нас было 52 карты. Оказалось, что полное нависание составило более чем две с четвертью карты.
Но почему 52 карты? А если бы было больше? Сотня? Миллион? Триллион? А предположим, что у нас имелся бы неограниченный запас карт — какого максимального нависания мы смогли бы тогда добиться?
Сначала взглянем на нашу постепенно растущую формулу. При 52 картах полное нависание составило
1/2 + 1/4 + 1/6 + 1/8 + 1/10 + 1/12 + 1/14 + 1/16 + … + 1/102.
Поскольку все знаменатели здесь четные, можно вынести одну вторую за скобки и переписать в виде
1/2∙(1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + … + 1/51).
Если бы у нас была сотня карт, то полное нависание составляло бы
1/2∙(1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + … + 1/99).
Имея в распоряжении триллион карт, мы добились бы нависания величиной в
1/2∙(1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + … + 1/999999999999).
Чтобы посчитать такое, требуется проделать немало арифметических действий, но у математиков есть способы спрямлять подобные вычисления, и я могу твердо заверить вас, что полное нависание в случае сотни карт будет лишь чуточку меньше, чем 2,58868875882, а для триллиона карт — на самую толику меньше, чем 14,10411839041479.
Полученные числа удивительны вдвойне. Во-первых, тем, что вообще удается добиться нависания в 14 с лишним карточных длин, пусть даже для этого понадобится триллион карт. Четырнадцать карточных длин — это более четырех футов, если брать стандартные игральные карты. А во-вторых, если об этом подумать, тем, что числа оказываются именно такими, а не большими. При переходе от 52 к 100 картам мы заработали дополнительное нависание лишь в одну треть длины карты (даже чуть-чуть меньше, чем в одну треть). А затем переход к триллиону — а колода в триллион стандартных игральных карт будет иметь такую толщину, что покроет большую часть расстояния до Луны, — принес нам всего лишь одиннадцать с половиной карточных длин.
Ну а если бы число карт у нас было неограниченным? Какого максимального нависания мы могли бы достичь? Замечательный ответ на этот вопрос состоит в том, что максимального нависания просто нет. Если в запасе имеется достаточное число карт, можно сделать нависание сколь угодно большим. Желаете получить нависание в 100 карточных длин? Пожалуйста, возьмите что-то около 405 709 150 012 598 триллионов триллионов триллионов триллионов триллионов триллионов карт — колоду, высота которой намного превысит размеры известной нам части Вселенной. А можно сделать и большее нависание, и еще большее — настолько большое, насколько захотите, если только у вас есть желание иметь дело с невообразимо большим числом карт. Нависание в миллион карт? Пожалуйста, но, правда, количество необходимых для этого карт будет таким большим, что только для записи этого числа понадобится нормального размера книга — в этом числе будет 868 589 цифр.
III.
Теперь нам предстоит сосредоточить свое внимание на выражении в скобках, а именно
1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + ….
Математики говорят, что это — ряд; ряд означает неограниченно продолжающееся суммирование членов, каждый из которых задается некоторым общим законом. В нашем случае члены ряда 1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, … — это обратные величины к обычным натуральным числам 1, 2, 3, 4, 5, 6, 7, ….
Ряд 1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + … играет в математике достаточно важную роль, чтобы иметь собственное название. Он называется гармоническим рядом.
Подведем промежуточный итог. Складывая достаточно большое число членов гармонического ряда, можно получить сколь угодно большой результат. У этой суммы нет предела.
Грубый, но распространенный и доходчивый способ выразить то же самое — это сказать, что гармонический ряд суммируется к бесконечности:
1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + … = ∞.
Хорошо воспитанных математиков учат морщиться при виде таких выражений; но я думаю, что с ними вполне можно иметь дело, если знать опасности, которые вас тут подстерегают. Леонард Эйлер, один из величайших математиков всех времен, использовал подобные выражения постоянно и весьма плодотворно. Но все же правильный, профессиональный математический термин, описывающий то, что здесь происходит, звучит так: гармонический ряд расходится.
Сказать-то я это сказал, но смогу ли я это доказать? Всем известно, что в математике каждый результат надо строго логически доказывать. Результат у нас такой: гармонический ряд расходится. Как его доказать?
Доказательство оказывается довольно простым и опирается только на самую элементарную арифметику. В Средние века его нашел французский ученый Никола Орем (ок. 1323-1382). Орем заметил, что сумма 1/3 + 1/4 больше чем 1/2; равным образом и 1/5 + 1/6 + 1/7 + 1/8 также больше чем 1/2; то же верно и для суммы 1/9 + 1/10 + 1/11 + 1/12 + 1/13 + 1/14 + 1/15 + 1/16. Другими словами, будем брать сначала 2, потом 4, потом 8, потом 16 и т.д. членов гармонического ряда и группировать их вместе; получится бесконечное число таких групп, каждая из которых в сумме превосходит одну вторую. Полная сумма, следовательно, должна быть бесконечной. Не стоит переживать из-за того, что размеры этих групп растут очень быстро: «в бесконечности» полно места, и неважно, сколько групп мы уже образовали, следующая все равно окажется на своем месте и к нашим услугам. Всегда есть возможность добавить еще одну а это и означает, что сумма растет неограниченно.
Данное Оремом доказательство расходимости гармонического ряда, по-видимому, пролежало невостребованным в течение нескольких столетий. Пьетро Менголи передоказал этот же результат в 1647 году с помощью другого метода. Сорок лет спустя Иоганн Бернулли дал доказательство еще одним, третьим, способом, а вскоре после того старший брат Иоганна Якоб предложил четвертый способ. Судя по всему, ни Менголи, ни братья Бернулли не знали о найденном в XIV веке доказательстве Никола Орема — одном из хорошо забытых шедевров средневековой математики. Тем не менее доказательство Орема остается наиболее прямым и изящным среди всех доказательств, и его, как правило, и приводят в современных учебниках.
IV.
В рядах изумляет не то, что некоторые из них расходятся, а то, что так делают не все ряды. Когда мы складываем бесконечное число слагаемых, разве мы не вправе ожидать, что и ответ будет бесконечен? То, что это не всегда так, легко проиллюстрировать.
Возьмем линейку, на которой делениями отмечены четверти, восьмые, шестнадцатые и т.д. (чем дальше, тем лучше — я изобразил линейку, на которой отмечены доли в одну шестьдесят четвертую). Поставим остро заточенный карандаш у самого первого деления на линейке — нуля. Подвинем карандаш на один дюйм вправо. Теперь карандаш указывает на деление, обозначающее один дюйм, а переместили карандаш мы также на один дюйм (рис. 1.7).
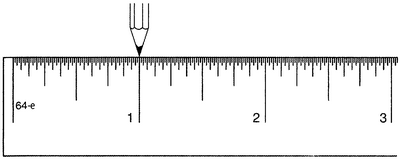
Рисунок 1.7.
Вслед за тем сдвинем карандаш вправо еще на полдюйма (рис. 1.8).
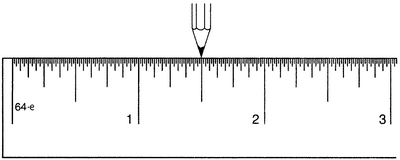
Рисунок 1.8.
Далее сдвинем еще на четверть дюйма вправо, потом на восьмую часть дюйма, потом на шестнадцатую, на тридцать вторую и на шестьдесят четвертую. Где теперь находится карандаш, видно на рисунке 1.9.
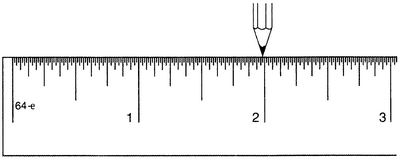
Рисунок 1.9.
А полное расстояние, на которое переместился карандаш, равно
1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64
что, как нетрудно посчитать, составляет 163/64. Понятно, что если продолжать в том же духе, то мы всякий раз будем оказываться все ближе и ближе к двухдюймовой отметке. Точно на нее мы никогда не попадем, но нет предела тому, насколько близко к ней можно подобраться. Можно приблизиться менее чем на миллионную долю дюйма, можно на триллионную; или на триллион триллион триллион триллион триллион триллион триллион триллион триллионную. Этот факт выражается таким образом:
1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + … = 2. (1.1)
Здесь имеется в виду, что слева от знака равенства выполняется суммирование бесконечного числа членов.
Важно осознать разницу между гармоническим рядом и этим новым рядом. В случае гармонического ряда сложение бесконечного числа слагаемых дало бесконечный результат. Здесь же сложение бесконечного числа слагаемых дает ответ 2. Гармонический ряд расходится. Наш новый ряд сходится.
В гармоническом ряде есть свое очарование, и он имеет прямое отношение к главной теме данной книги — Гипотезе Римана. Но вообще-то математиков больше интересуют сходящиеся ряды, нежели расходящиеся.
V.
Предположим теперь, что вместо того, чтобы передвигаться направо на один дюйм, потом на полдюйма, потом на четверть дюйма и т.д., мы будем менять направление: дюйм вправо, полдюйма влево, четверть дюйма вправо, одна восьмая дюйма влево… После семи шагов мы попадем в точку, показанную на рисунке 1.10.
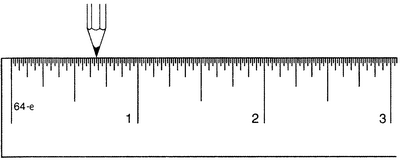
Рисунок 1.10.
С математической точки зрения сдвиг налево означает сдвиг направо на отрицательную величину, и поэтому наши передвижения выражаются такой суммой:
1 − 1/2 + 1/4 − 1/8 + 1/16 − 1/32 + 1/64,
что на самом деле равно 43/64. В действительности несложно доказать — и мы это сделаем в одной из последующих глав, — что если продолжать прибавлять и вычитать до бесконечности, то результат будет таким:
1 − 1/2 + 1/4 − 1/8 + 1/16 − 1/32 + 1/64 − 1/128 + … = 2/3. (1.2)
VI.
Теперь представим себе, что вместо линейки с делениями, обозначающими половины, четверти, восьмые, шестнадцатые и т.д. доли дюйма, в руках у нас линейка с делениями в третьи, девятые, двадцать седьмые, восемьдесят первые и т.д. доли. Другими словами, вместо половинок, половин от половин, половин от половин от половин… у нас нанесены трети, трети от третей, трети от третей от третей и т.д. Будем теперь упражняться в том же, что и раньше, — переносить карандаш сначала на дюйм, потом на треть дюйма, потом на одну девятую, потом на одну двадцать седьмую (рис. 1.11).
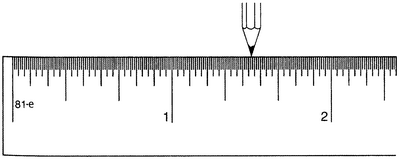
Рисунок 1.11.
Совсем несложно убедиться, что если продолжать такую операцию до бесконечности, то получится полная сумма в 11/2 дюйма. Другими словами,
1 + 1/3 + 1/9 + 1/27 + 1/81 + 1/243 + 1/729 + 1/2187 + … = 11/2. (1.3)
А можно, конечно, и на нашей новой линейке менять направление движения: направо на дюйм, налево на треть, направо на одну девятую, налево на одну двадцать седьмую и т.д. (рис. 1.12).
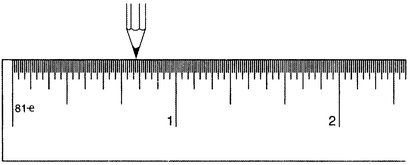
Рисунок 1.12.
Соответствующая арифметика, возможно, не так уж прозрачна, но, как бы то ни было, результат имеет вид
1 − 1/3 + 1/9 − 1/27 + 1/81 − 1/243 + 1/729 − 1/2187 + … = 3/4. (1.4)
Итак, у нас имеются четыре сходящихся ряда: первый подкрадывается слева все ближе и ближе к 2, второй приближается к 2/3 попеременно то слева, то справа, третий подбирается слева все ближе и ближе к 11/2, а четвертый приближается к 3/4 попеременно то слева, то справа. А перед этим мы познакомились с одним расходящимся рядом — гармоническим.
VII.
При чтении математической литературы полезно знать, в какой области математики вы находитесь — какую часть из этого обширного предмета изучаете. Та область, где обитают бесконечные ряды, в математике называется анализом. Обычно считается, что анализ занимается изучением бесконечного, т.е. бесконечно большого и бесконечно малого (инфинитезимального). Когда Леонард Эйлер — о котором будет много всего сказано ниже — в 1748 году опубликовал свой превосходный первый учебник по анализу, он назвал его просто Introductio in analys in infinitorum — «Введение в анализ бесконечного».
Однако понятия бесконечного и инфинитезимального привели в начале XIX века к возникновению серьезных проблем в математике и в конце концов были полностью сметены с дороги в ходе большой реформы математики. В современный анализ эти концепции не допускаются. Но они застряли в словарном запасе математиков, и в этой книге я нередко буду использовать слово «бесконечность». Надо только помнить, что оно представляет собой просто удобное и выразительное сокращение для более строгих понятий. Каждое математическое утверждение, где присутствует слово «бесконечность», можно переформулировать, не используя этого слова.
Когда мы говорим, что сумма гармонического ряда равна бесконечности, на самом деле имеется в виду, что если задаться сколь угодно большим числом S, то сумма гармонического ряда рано или поздно превысит S. Видите? Никаких «бесконечностей». Во второй трети XIX века анализ был целиком переписан на языке подобного рода. Если какое-то выражение нельзя переписать таким образом, то оно не допускается в современную математику. Далекие от математики люди иногда меня спрашивают: «Раз вы знаете математику, ответьте на вопрос, который меня всегда занимал: сколько будет бесконечность разделить на бесконечность?» На это я могу ответить только: «Вы произносите слова, которые не имеют никакого смысла. Это не математическая фраза. Вы говорите о „бесконечности“ так, как если бы это было число. Но это не число. С таким же успехом вы могли бы спросить „Сколько будет истина разделить на красоту?“ Я ничего не могу по этому поводу сказать. Я умею делить только числа, а „бесконечность“, „истина“, „красота“ — это не числа».
Каково же тогда современное определение анализа? Для наших целей, как мне кажется, подойдет такое определение: это изучение пределов. Понятие предела лежит в основе анализа. Например, все дифференциальное и интегральное исчисление, составляющее наиболее значительную часть анализа, основано на понятии предела.
Рассмотрим такую числовую последовательность: 1/1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, 577/408, 1393/985, 3363/2378, …. Каждая следующая дробь получена из предыдущей по простому правилу: новый знаменатель равен сумме старого числителя и старого знаменателя, а новый числитель равен сумме старого числителя и удвоенного старого знаменателя. Эта последовательность сходится к квадратному корню из числа 2. Например, возведение в квадрат числа 3363/2378 дает 11309769/5654884, что равно 2,000000176838287…. Говорят, что предел этой последовательности равен √2.
Рассмотрим еще один пример последовательности: 4/1, 8/3, 32/9, 128/45, 768/225, 4608/1575, 36864/11025, 294912/99225, …. Здесь N-й член последовательности получается так: если N четно, то умножаем предыдущий член на N/(N + 1), а если N нечетно, то умножаем предыдущий член на (N + 1)/N. Такая последовательность сходится к числу π. Последняя из приведенных дробей равна 2,972154… (данная последовательность сходится очень медленно). А вот еще пример: 11, (11/2)2, (11/3)3, (11/4)4, (11/5)5, … — эта последовательность сходится к числу, которое примерно равно 2,718281828459. Это необычайно важное число, и мы будем использовать его в дальнейшем.
Стоит заметить, что приведенные только что примеры — это примеры последовательностей, т.е. наборов чисел, записанных через запятую. Это не ряды, члены которых надо складывать. Но с точки зрения анализа ряд — это все-таки слегка замаскированная последовательность. Утверждение «ряд 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + … сходится к 2» математически эквивалентно такому утверждению: «последовательность 1, 11/2, 13/4, 17/8, 115/16, 131/32, … сходится к 2». Четвертый член этой последовательности представляет собой сумму первых четырех членов ряда и т.д. (Название последовательности такого типа на математическом языке — последовательность частичных сумм данного ряда.) Аналогично, утверждение «гармонический ряд расходится» эквивалентно утверждению «последовательность 1, 11/2, 15/6, 21/12, 217/60, 227/32, … расходится». В этой последовательности N-й член равен предыдущему плюс 1/N.
Все это относится к анализу, т.е. к изучению пределов — того, как именно числовая последовательность может приближаться к некоторому предельному числу, никогда точно его не достигая. Когда говорится, что последовательность продолжается неограниченно, имеется в виду, что, сколько бы членов мы уже ни выписали, всегда можно написать следующий. Когда говорится, что последовательность имеет предел, равный a, имеется в виду, что, какое бы малое число x мы ни взяли, начиная с некоторого момента каждый член последовательности будет отличаться от a на величину, меньшую, чем выбранное x. А если вы предпочитаете говорить «Последовательность стремится к бесконечности» или «Предел N-го члена при N, стремящемся к бесконечности, есть a», то вы вправе так выражаться, если вы сами осознаете, что это просто удобная фигура речи.
VIII.
Традиционное деление на дисциплины внутри математики таково.
• Арифметика — наука о целых числах и дробях. Пример теоремы из арифметики: вычитание нечетного числа из четного дает в ответе нечетное число.
• Геометрия — наука о фигурах в пространстве — точках, линиях, кривых, трехмерных объектах. Пример теоремы: сумма углов треугольника на плоскости равна 180 градусам.
• Алгебра — использование абстрактных символов для представления математических объектов (чисел, линий, матриц, преобразований) и изучение правил, по которым эти символы можно комбинировать. Пример теоремы: для любых двух чисел x и y имеет место равенство (x + y)×(x − y) = x2 − y2.
• Анализ — наука о пределах. Пример теоремы: гармонический ряд расходится (т.е. неограниченно возрастает).
Кроме этого, в современной математике есть, конечно, много всего другого. Например, в ней есть теория множеств, созданная Георгом Кантором в 1874 году а есть «основания» — раздел, который в 1854 году усилиями англичанина Джорджа Буля отделился от классической логики и в котором исследуются логические основы всех математических концепций. Сами традиционные категории также разрослись и стали включать в себя целые новые темы — геометрия вобрала в себя топологию, алгебра — теорию игр и т.д. Еще до начала XIX века происходило значительное просачивание из одной области в другую. Например, тригонометрия (само слово было впервые употреблено в 1595 году) содержит в себе элементы и геометрии, и алгебры. В XVII веке Декарт арифметизировал и алгебраизировал значительную часть геометрии (правда, чисто геометрические доказательства в стиле Эвклида сохранили свою популярность до наших дней за их ясность, изящество и остроумие).
Как бы то ни было, четырехчленное деление сохраняет свою роль в качестве первоначальной ориентировки в математике. Эта классификация полезна и для понимания одного из величайших завоеваний математики XIX столетия, о котором мы далее будем говорить как о «великом соединении» — привязывании арифметики к анализу, что привело к созданию совершенно новой области исследований — аналитической теории чисел. Позвольте познакомить вас с человеком, который одной только публикацией статьи объемом в восемь с половиной страниц дал жизнь аналитической теории чисел, успешно развивающейся и поныне.

