Приложение 2. Гипотеза Римана в песне

Где же нули у функции дзета?

(на мотив Sweet Betsy from Pike)

1   Где же нули у функции дзета?
    Нам Риман оставил догадку про это:
    «На критической линии, там они все,
    А их плотность — один-на-два-π ln T».

5   И эта гипотеза, словно заноза,
    Многих людей довела до психоза.
    Стремились они дать строгий расчет,
    Что происходит, когда t растет.

     Ландау, и Бор, и Крамер, и Харди
10 Среди одержимых шли в авангарде.
     Но все-таки даже они не смогли
     Уверенно все перечислить нули.

     Впоследствии Харди сумел доказать,
     Что на этой прямой их несметная рать,
15 Но его теорема все ж не исключает,
     Что где-то еще те нули обитают.

     Пусть P будет π минус Li — вот прелестно!
     Но как там с порядком P — неизвестно.
     Если корень из x ln x — потолок,
20 То Гипотезу Римана вывесть я б смог.

     Вопрос про μ(σ) задал Линделёф;
     Над ним потрудилось немало умов.
     Проверим критическую полосу,
     И сколько нулей там — как на носу.

25 Но функция эта ведет себя сложно,
     Ее изучили, насколько возможно.
     «График должен быть выпуклым, — смог он сказать, —
     Если сигма сама превосходит 0,5».

     Так где же нули у функции дзета?
30 Даже через столетие все нет ответа.
     А ТРПЧ можно все улучшать,
     Но контур обязан нули избегать.

     Тем временем Вейль обратился к предмету,
     Используя более хитрую дзету.
35 Коль характеристика поля равна
     Простому числу — теорема верна.

     Мораль этой притчи нетрудно понять,
     И всем юным гениям следует знать:
     Если не выручает обычный подход,
40 То по модулю p — авось повезет!

Том М. Апостол, перевод Сергея Ельницкого

Where are the zeros of zeta of s?

Where are the zeros of zeta of s?
G.F.B. Riemann has made a good guess:
«They're all on the critical line,» stated he,
«And their density's one over two pi log T».

This statement of Riemann's has been like a trigger,
And many good men, with vim and with vigor,
Have attempted to find, with mathematical rigor,
What happens to zeta as mod t gets bigger.

The efforts of Landau and Bohr and Cramér,
Hardy and Littlewood and Titchmarsh are there.
In spite of their effort and skill and finesse,
In locating the zeros there's been no success.

In 1914 G.H. Hardy did find,
An infinite number that lie on the line.
His theorem, however, won't rule out the case,
That there might be a zero at some other place.

Let P be the function pi minus Li;
The order of P is not known for x high.
If square root of x times log x we could show,
Then Riemann's conjecture would surely be so.

Related to this is another enigma,
Concerning the Lindelöf function mu sigma,
Which measures the growth in the critical strip;
On the number of zeros it gives us a grip.

But nobody knows how this function behaves,
Convexity tells us it can have no waves.
Lindelöf said that the shape of its graph
Is constant when sigma is more than one-half.

Oh, where are the zeros of zeta of s?
We must know exactly. It won't do to guess.
In order to strengthen the prime number theorem,
The integral's contour must never go near 'em.

André Weil has improved on old Riemann's fine guess
By using a fancier zeta of s.
He proves that the zeros are where they should be,
Provided the characteristic is p.

There's a moral to draw from this long tale of woe
That every young genius among you must know:
If you tackle a problem and seem to get stuck,
Just take it mod p and you'll have better luck.

Примечания

Мотив. Sweet Betsy from Pike — песня, которую поют на этот мотив в Америке. Однако мелодия старше, чем слова. Впервые она прозвучала в английской песенке Villikens and his Dinah, популярной в середине XIX века. (Из этой песенки, кстати, взято имя кошки в книгах Льюиса Кэрролла об Алисе. Villikens and his Dinah была любимой песней Алисы Лидделл — девочки, которая вдохновила его на написание книг, и у нее и в самом деле была кошка по имени Дина.) Если ваше обучение в Британии включало в себя членство в школьном клубе регби, то вы, скорее всего, распознаете эту мелодию как мелодию известной печальной баллады, начинающейся словами О Father, О Father, I've come to confess. I've left some poor girl in a hell of a mess.

Строка 1. См. главу 5.vii.

Строка 2. Полное имя Римана было Георг Фридрих Бернхард Риман (глава 2.iii). Насколько известно, он всегда пользовался только именем Бернхард.

Строка 3. По поводу «критической прямой» (она же критическая линия) см. главу 12.iii, рисунок .

Строка 4. Это следует сравнить с утверждением из главы 13.viii, что на высоте T вдоль критической прямой средний интервал между нулями ~2π/ln (T/2π). Это означает, что на единицу длины вдоль прямой приходится ~(1/2π)/ln (T/2π) нулей. Это автор песни и имеет в виду под «плотностью». Заметим, что, согласно правилам обращения с логарифмами, ln (T/2π) равен ln T − ln (2π), т.е. ln Т − 1,83787706…. Умножив это на 1/2π, получим (1/2π)ln T − 0,29250721…. По мере роста T растет (хотя и намного медленнее) и ln T, так что слагаемое величины 0,29250721… становится совершенно несущественным. Следовательно, плотность равна «один-на-два-пи эль-эн T».

Строка 8. В оригинале обозначение mod t использовано для модуля числа t, определенного в главе 11.v. Когда, как в данном случае, под t понимается вещественное число, mod t — в нормальных обозначениях |t| — выражает просто величину t без учета знака. Как отмечалось в главе 16.iv, t (или T) — довольно стандартное обозначение в теории дзета-функции, когда говорят о больших высотах вдоль критической прямой (или, более общим образом, как видно из обсуждения ГЛ в примечаниях к строчкам 21-28, о мнимой части аргумента дзета-функции).

Строка 9. Харальд Бор (глава 14.iii) и Эдмунд Ландау доказали в 1913 году важную теорему о функции S (см. главу 22.iv), которая гласит, что если дзета-функция имеет лишь конечное число нулей вне критической прямой, то функция S(t) неограничена, когда t стремится к бесконечности. Упоминавшееся в главе 22.iv доказательство Сельберга 1946 года, что S(t) неограничена, — более сильный результат, поскольку не требует указанного условия. По поводу Крамера см. главу 20.vii. Помимо разработки упомянутой там «вероятностной модели» для распределения простых чисел Крамер также доказал и один менее значительный результат о функции S: если ГЛ (см. примечания к строчкам 21-28) верна, то S(t)/ln t стремится к нулю, когда t стремится к бесконечности. По поводу Литлвуда и Харди см. главу 14; по поводу Титчмарша — главу 16.v.

Строки 13-16. Глава 14.v.

Строка 17. Чтобы попасть в размер, термин Li здесь надо произносить как как ell-eye (в оригинале, и как «ли» в переводе. — Примеч. перев.). Далее автор песни обсуждает остаточный член π(x) − Li(x), который мы подробно рассматривали в главе 21.

Строка 18. «Как там с порядком P — неизвестно» означает, что «P есть Ο большое от… от чего? — неизвестно». По поводу Ο большого см. главу 15.ii-iii; при этом имеются в виду большие значения x.

Строки 19-20. Если бы удалось доказать, что π(x) − Li(x) = Ο(√x∙ln x) (другими словами, на разность имеется ограничение, т.е. «потолок»), то и ГР была бы доказана. В этом заключается результат, обратный результату фон Коха 1901 года, приведенному в главе 14.viii. Там это не упомянуто, но если формула фон Коха верна, то верна и ГР. Они следуют друг из друга.

Строки 21-28. Следующие несколько строк целиком посвящены гипотезе Линделёфа (ГЛ) — знаменитому предположению в теории дзета-функции. Его гипотеза касается роста дзета-функции в вертикальном направлении — т.е. вверх по вертикальной прямой в комплексной плоскости.

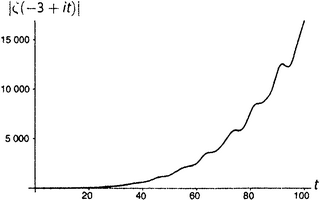
Рисунок П1.

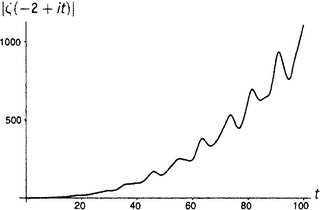
Рисунок П2.

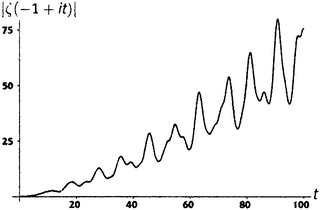
Рисунок П3.

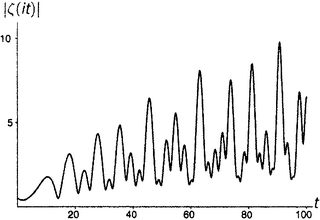
Рисунок П4.

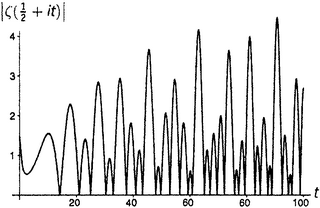
Рисунок П5.

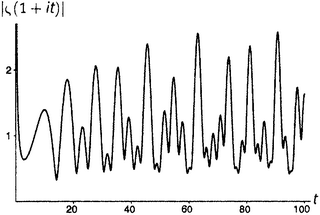
Рисунок П6.

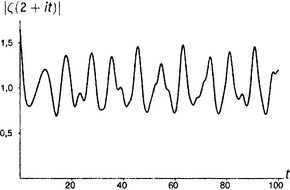
Рисунок П7.

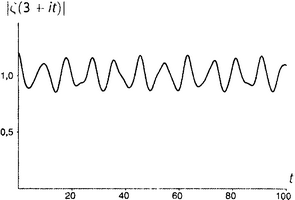
Рисунок П8.

Рисунок П9. Функция Линделёфа.

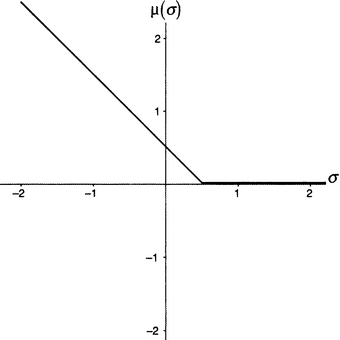
Рисунок П10. Гипотеза Линделёфа.

Строка 24. Можно доказать, что ГЛ эквивалентна утверждению, которое ограничивает число нулей дзета-функции вне критической прямой. Если ГР верна, то, конечно, таких нулей не должно быть вовсе. Но как уже отмечалось, из доказательства ГР последует и ГЛ.

Строка 31. «А ТРПЧ можно все улучшать» — т.е. получить наилучшее возможное выражение типа Ο большого для остаточного члена.

Строка 32. При обычном интегрировании, как мы определили его в главе 7.vii, интегрируют вдоль оси x, от некоторого числа a до какого-то большего числа b. При наличии комплексных переменных можно интегрировать вдоль некоторого контура — т.е. прямой или кривой линии — в комплексной плоскости, от некоторой точки на этом контуре до какой-нибудь другой точки. Обычно контур при этом надо выбирать: результат интегрирования может зависеть от того, по какому именно контуру происходит интегрирование. Контурное интегрирование — одно из основных средств в аналитической теории чисел (и вообще в теории функций комплексной переменной). Для получения определенных результатов об остаточном члене надо интегрировать по контуру, который не проходит через нули дзета-функции.

Строка 33. «Вейль обратился к предмету…». В этих последних куплетах говорится об алгебраическом подходе, упоминавшемся в главе 17.iii, и о результате А. Вейля 1942 года.

Строка 34. «Используя более хитрую дзету» — другими словами, один из упоминавшихся в главе 17.iii аналогов дзета-функции, связанных с конечными полями.

Строка 35. Мы определили характеристику поля в главе 17.ii. Аналоги ГР были доказаны только для дзета-функций, связанных с полями ненулевой характеристики — т.е. характеристики, равной некоторому простому числу p.

Строка 36. «…теорема верна». Благодаря А. Вейлю известно, что аналоги ГР для этих специальных полей верны.

Строка 40. Слова «по модулю p» используются здесь в смысле арифметики циферблата из главы 6.viii; как отмечалось в главе 17.ii, здесь имеется связь с теорией полей.

Отправить