В этом дополнении мы обсуждаем координаты для чёрной дыры Шварцшильда, свободные от дефектов на горизонте. Их предложил Леметр, как систему отсчёта, сопутствующую свободно падающим наблюдателям. Смысл её в том, что в каждую точку пространства помещается наблюдатель. Наблюдатели никак не взаимодействуют между собой, они лишь свободно падают к центру, формально представляя собой точки. Каждому наблюдателю приписываются три пространственных координаты, которые вместе образуют пространственные координаты всего пространства–времён и. А собственное время каждо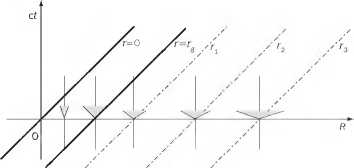

Рис. Д1. Пространство–время геометрии Шварцшильда в сопутствующих координатах Леметра

го наблюдателя вместе определяет координатное время новой системы отсчёта. Форма решения сохраняет сферическую симметрию, поэтому можно сказать, что Леметр сделал переход от шварцшильдовых координат t и r к координатам сопутствующих наблюдателей (сопутствующей системе отсчёта) τ и R.

Мы не приводим форму решения Леметра, а вот диаграмма на рис. 8.2 в его координатах принимает форму, представленную на рис. Д1. Обсудим её. Наклонные на рис. Д1 соответствуют вертикальным линиям постоянных значений координаты r на рисунке 8.2, включая линии горизонта r = r_g и сингулярности r =0. Вертикальные на рис. Д1 — мировые линии сопутствующих наблюдателен. Как видно, они без помех пересекают горизонт.

Проследим за формой световых конусов на рис. Д1. Вне горизонта наклон «лепестков» превосходит 45°, на горизонте он равен 45°, а под горизонтом становится все меньше: конусы сужаются при приближении к «центру». Поскольку распространение лучей света происходит как раз по направлению конусов, а материальных частиц — по мировым линиям внутри конусов, то ясно, что вне горизонта r = r_g возможно движение с удалением от горизонта во внешнюю область. По достижении горизонта такое движение невозможно. Под горизонтом становится неизбежным движение к «центру».