Нулевая частота означает, что нет никакого сигнала вообще! Из-под сферы радиуса r_g световые сигналы не выходят, гравитационные силы не дают им вырваться во внешнюю окрестность. То есть, действительно, это сфера, где вторая космическая скорость становится равной скорости света. Поэтому из-под сферы радиуса r_g невозможно распространение наружу никакой формы материи. Таким образом, эта сфера оказывается барьером, за который внешний наблюдатель не в состоянии заглянуть. Именно поэтому она получила удачное название горизонта событии, а сам объект стали называть чёрной дырой.

Термин чёрная дыра подсказал известному американскому физику–теоретику Джону Уилеру (1911–2008) один из студентов на конференции в 1967 году. Но ещё ранее, в 1964 году, его использовала Анна Ивинг в докладе на собрании Американской ассоциации содействия науке.

До сих пор мы рассматривали фиксированные точки пространства и наблюдателей, связанных с ними Теперь давайте проследим за свободно падающим телом. Пусть падение начинается из состояния покоя из удалённой области, где почти нет искривления, откуда мы будем отслеживать его траекторию. В восприятии удалённого наблюдателя история падения будет следующей. Сначала движение не будет вызывать удивления, Скорость будет нарастать медленно, затем все быстрее и быстрее, вполне соответствуя закону всемирного тяготения. Затем, на расстояниях от центра, сравнимых с гравитационным радиусом, нарастание скорости падения станет катастрофическим. Здесь мы тоже не очень удивимся, мы объясним это тем, что из зоны соответствия с гравитацией Ньютона объект попал в зону сильных искривлений. А на расстояниях долей гравитационного радиуса от горизонта событий он, к нашему изумлению, начнёт резко тормозить и все медленней приближаться к горизонту событий, а в результате, никогда его не достигнет. Но здесь тоже нечего удивляться, недавно мы установили, что для удалённого наблюдателя все процессы при приближении к горизонту событий замирают, падение тела — не исключение.

Эффект того, что из-под горизонта событий ничего не выходит наружу, мы объяснили наличием чрезвычайно сильного гравитационного воздействия. Этот ответ, конечно, правильный, поскольку ничего, кроме гравитации, не рассматривается. Однако он не конструктивный, так как не позволяет понять механизм тех явлений, о которых мы только что говорили. Нет никакого представления о том, что происходит под горизонтом, и происходит ли вообще что-то. С другой стороны, мы договорились, что в эйнштейновской теории гравитационных сил, как таковых, нет вообще. Есть искривление пространства–времени. Поэтому, давайте, шаг за шагом перейдём к описанию в рамках геометрической теории.

Мы уже убедились, что в СТО использование светового конуса помогает понять многие явления. В ОТО, в искривлённом пространстве–времени, имеет больший смысл представлять его не на всей диаграмме, а в окрестности каждой мировой точки. Это будет локальный световой конус, образованный касательными к световым геодезическим в данной точке. Уравнение светового конуса имеет простой вид — интервал приравнивается нулю: ds = 0.

На рис. 8.2 схематически изображены световые конусы для геометрии Шварцшильда. Предполагая, что движения происходят по радиальным направлениям, диаграмма представлена в координатах r и t. Эти координаты для удалённого наблюдателя в его собственной системе отсчёта определяют истинные расстояние и время. Поэтому картина физических явлений, представленная с помощью r и t, — это как раз та картина, которую будет воспринимать удалённый наблюдатель. На рисунке видно, что на значительном удалении «лепестки» конуса расположены под углом 45°, то есть так, как в плоском пространстве-времени. Вертикальные линии соответствуют тем самым зафиксированным (неподвижным) наблюдателям, о которых мы говорили недавно. По мере приближения к чёрной дыре конус становится все уже, на горизонте

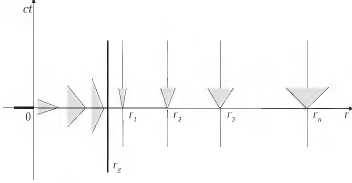
Рис 8.2. Пространство–время геометрии Шварцшильда в координатах удалённого наблюдателя

он «слипается» и превращается в одну вертикальную линию. Вертикальная линия для удалённого наблюдателя означает, что свет «остановился», его скорость стала «нулевой». Это и означает, что на горизонте все явления замораживаются. Расчёт нулевой геодезической показывает, что для удалённого наблюдателя свет никогда не достигнет горизонта.

Частично такое поведение световых конусов связано с эффектом замедления времени при приближении к гравитирующему центру. Однако, полностью его форма, как мы уже говорили, определяется условием ds = 0, как раз оно определяет «видимую» скорость света для удалённого наблюдателя: v_c = c (1 — r_g/r). На значительном удалении от центра скорость близка к c, по мере приближения к центру она уменьшается, а на горизонте, действительно, обращается в нуль. Это прямо связано с формой световых конусов на рис. 8.2. Скорость материальных частиц всегда меньше скорости света (мировая линия физической частицы, находится между створками светового конуса), поэтому их «видимые» предельные скорости тоже уменьшаются при продвижении к центру, и они тоже никогда не достигнут горизонта в координатах r и t. Этот вывод ещё раз подтверждает наше описание свободного падения к горизонту с точки зрения удалённого наблюдателя.

Далее продолжим наш мысленный эксперимент, теперь «сожмём» все вещество сферического объекта не только до гравитационного радиуса, а вообще, до «точки» r = 0. То есть все пространство–время будем рассматривать как вакуумное. Формально мы имеем право это сделать, поскольку решение Шварцшильда как раз вакуумное. Обратимся к выражению для метрики. Мы уже отметили, что на горизонте коэффициент g₀₀ при c²dt² обращается в нуль, а коэффициент g₁₁ при dr² становится бесконечным. Мало того, есть особенность и в «точке» r = 0: здесь, наоборот, g₀₀ становится равным «минус бесконечности», g₁₁ — равным нулю. Вспомним, что для «обычного» тела, о котором речь шла в начале параграфа, не возникло никаких особенностей. Далее мы обсудим смысл как особенности на горизонте, так и особенности в центре.

Начнём с горизонта. Вспомним, что в пространстве Минковского физические сущности пространства и времени остаются разными, несмотря на их релятивистский характер. Это проявляется в том, что временная и пространственная части входят в выражение для интервала с разными знаками: первая — со знаком «плюс», вторая — со знаком «минус». Это так и есть для решения Шварцшильда на удалении от горизонта (в «регулярной» области пространства). Временная часть, определяемая коэффициентом g₀₀ при c²dt², действительно, положительна, а пространственная, определяемая коэффициентом g₁₁ при dr², — отрицательна.

А что будет под горизонтом? Там ситуация изменилась: в выражении для интервала мы должны учесть r < r_g, тогда коэффициент g₀₀ при с²dt²- становится отрицательным, а коэффициент g₁₁ при dr² становится, наоборот, — положительным. А это, как только что мы обсудили, означает, что под горизонтом координата t становится пространственной, а координата r — временной! Теперь, учитывая этот факт, построим световые конусы под горизонтом. Поскольку на диаграмме координаты r и t поменяли смысл, световые конусы как бы лягут на бок, с внутренней стороны на горизонте их створ равен 180°, затем приближаясь к центру r = 0, створ уменьшается. Как всегда, мировая линия реальной физической частицы должна быть внутри створа светового конуса. Наконец, при r = 0 лепестки конусов окончательно «слипаются», как показано на рис. 8.2. Расположение и форма световых конусов под горизонтом говорят о двух вещах. Первое, действительно, ни лучи света, ни какая материальная частица не могут покинуть горизонт и область под ним; второе, все частицы и свет, оказавшись под горизонтом, неминуемо достигнут начала координат при r = 0. Действительно, створ конуса всегда направлен к линии r = 0.

Мы видим, что под горизонтом нет препятствий для движения частиц, хотя и выглядит это несколько необычно. С другой стороны, сигналы извне не могут преодолеть горизонт. Происходит разрыв мировых линий световых лучей и падающих частиц. Самое время обсудить особенность на горизонте. Попытаемся понять, что на горизонте и в его окрестности происходит в реальности.

Придётся вернуться к истокам ОТО и вспомнить, что основной характеристикой пространства–времён и является его искривление (кривизна), которое определяется тензором кривизны Римана. Но вычисление компонент тензора Римана на горизонте и в его окрестности ничего необычного не обнаруживает. До горизонта, на горизонте и под ним кривизна не испытывает никаких разрывов, ведёт себя вполне плавно, постепенно увеличиваясь по мере приближения к центру, Дело в том, что координаты удалённого наблюдателя (а это координаты плоского пространства–времени), в которых и записано решение Шварцшильда, не вполне годятся для описания явлений в окрестности горизонта. Это значит, что нужно найти координаты, которые не имели бы этого дефекта.

Вспомним, что истинное время каждого наблюдателя для него самого всегда имеет одно и то же течение, в том числе и совсем близко к горизонту, А возможно, и на горизонте, почему нет? Поэтому в искомых координатах можно использовать собственное время свободно падающих (сопутствующих) наблюдателей как новую временную координату. Такие координаты для решения Шварцшильда, свободные от дефектов на горизонте, предложил в 1938 году бельгийский астроном и математик Жорж Леметр (1894–1966). В его сопутствующей системе отсчёта мировые линии частиц и световых лучей перестают испытывать разрыв на горизонте — они его свободно пересекают. Диаграмма в координатах Леметра обсуждается в Дополнении 5.

Что же испытают наблюдатели, минуя горизонт? Все зависит от кривизны этого горизонта. Если чёрная дыра огромная, то локально горизонт довольно плоский, и наблюдатель никак не отреагирует на его пересечение. Если уменьшать чёрную дыру, то в определённый момент наблюдатель начнёт ощущать действие приливных сил. Его начнёт «растягивать» по радиусу и «обжимать» с боков. Но эти явления могут начаться и до достижения горизонта, они с ним не связаны. Ключевым моментом является следующее. Оказавшись под горизонтом, наблюдатель имеет возможность получить сигнал из внешнего мира, но не имеет возможности послать сигнал наружу.

Наконец, обсудим особенность в «центре» r = 0. Пока мы получили её, проводя мысленный эксперимент. А может ли такая особенность образоваться в реальности? Снова вернёмся к примеру с «обычным» телом, который обсуждался в начале этой главы. Такой объект описывается внутренним решением, которое статично, не имеет особенностей и «сшивается» с внешним решением Шварцшильда. Внутреннее решение получено с учётом уравнения состояния вещества тела. В этом случае уравнение состояния определяет такое давление, что оно противостоит гравитационному сжатию. Именно поэтому объект статичен. Всегда ли это возможно? Забегая вперёд, где эта проблема обсуждается, скажем: нет, не всегда. Если масса тела равна или превышает пять солнечных масс, то не существует такого состояния вещества, чтобы его давление могло противостоять гравитационному сжатию. Что произойдёт, если тело такой массы образуется, как остаток погибшей звезды? Ясно — тело начнёт сжиматься. Давайте проследим за этим сжатием, только не издалека (мы убедились, что удалённый наблюдатель для этого не годится), а с помощью наблюдателя, посаженного на поверхность этого тела. Сначала наблюдатель вместе с остатком звезды достигнет горизонта. До этого он имеет принципиальную возможность спастись на сверхмощной ракете, покинув злополучный коллапса р. Но сравнявшись с горизонтом, он неминуемо вместе с остатком звезды «свалится» в центр. Фатальное слово «неминуемо» вполне научно обосновано, расположение световых конусов под горизонтом говорит об этом однозначно.

Итак, действительно, все может свалиться в «центр» r = 0. Но можно ли сказать, что в результате образуется особенность, именно, в «точке». Строго говоря, нет. Дело в том, что при таком сжатии плотность и давление вещества достигают величин, для которых известные законы физики уже не работают. Скорее всего, пространство и время перестают быть классическими, поэтому в непосредственной близости от центра, куда все свалилось, уже нельзя построить тех самых световых конусов. Так что разумнее говорить о сверхплотном образовании в центре, физика которого пока не изучена.

С этими оговорками обсудим, тем не менее, идеализированную точечную особенность. Снова, как в случае горизонта, посчитаем компоненты тензора кривизны, Но теперь, в отличие от горизонта, получим, что кривизна обращается в бесконечность. А это означает, что такая особенность не может быть «ликвидирована» с помощью перехода к другим координатам, как особенность на горизонте. Таким образом, для r = 0 имеем особенность, которую часто называют истинной сингулярностью. Далее, поскольку получается, что вся масса объекта сосредоточена в нулевом объёме, то и плотность вещества также обращается в бесконечность. Отметим, что прямая r = 0 на диаграмме рисунка 8.2 пересекает «лепестки» близких световых конусов. То есть по прямой r = 0 никакие сигналы не распространяются и частицы не движутся. Исходя из этого, на умозрительном уровне (без необходимой научной строгости) сингулярность r = 0 можно интерпретировать, как часть пространства с нулевым объёмом, бесконечной плотностью и кривизной, на котором «заканчивается» течение времени.