Пример невидимой звезды Мичелла–Лапласа, хотя и основан на теории, которая не в состоянии дать правильные решения для реальных чёрных дыр со всем многообразием эффектов и необычных свойств, демонстрирует самое главное их свойство. Чёрная дыра обладает настолько сильным гравитационным притяжением, что нет сил в природе, которые бы могли его превозмочь.

Теперь самое время перейти к чёрным дырам в ОТО. Сначала нужно вернуться к решению Шварцшильда, повторим запись интервала для него:

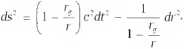
До сих пор мы использовали его для описания искривлённого пространства–времени вокруг (вне) «обычных» статичных сферически симметричных тел, размеры которых существенно больше соответствующего гравитационного радиуса r_g. Как видно, при этом условии внешнее решение не имеет особенностей. А как описывает теория Эйнштейна такие системы полностью? Внешнее вакуумное решение нужно дополнить внутренним, которое будет отличаться от решения Шварцшильда. Снова ограничимся условиями сферической симметрии и статичности, но к ним добавим условия «сшивки» с внешним решением на границе. Чтобы получить внутреннее решение, используют уже не вакуумные уравнения Эйнштейна, а уравнения ОТО с материей (веществом тела). Необходимо определиться также с уравнениями для самой материи. Как минимум, это уравнение состояния (связи между давлением и плотностью). Затем все уравнения решаются совместно. Такие внутренние решения найдены, они также не имеют никаких особенностей, то есть весь физический объект (тело с внешним полем) получается вполне регулярным, и пока нет речи о чёрных дырах.

Зададимся вопросом: что произойдёт, если, сохраняя массу, взять тело меньшего радиуса, и, соответственно, меньшего объёма? При несущественном сжатии ничего особенного не произойдёт, Внешнее искривлённое пространство–время будет представлено все тем же решением Шварцшильда. Если кто-то очень сильный «уплотнит» Солнце, сожмёт его в несколько раз, сохраняя сферическую симметрию, то это никак не повлияет на движение планет — они будут двигаться по тем же орбитам. Обсуждая чёрные дыры Мичелла–Лапласа, мы отметили, что вторая космическая скорость тем больше, чем меньше радиус тела при той же массе. Поэтому, стремясь увеличить вторую космическую скорость, давайте, мысленно (пренебрегая реальными условиями состояния вещества) уменьшать радиус тела, сохраняя массу.

До каких пор интересно продолжать этот мысленный процесс? Как видно, при r = r_g решение Шварцшильда перестаёт быть регулярным: коэффициент временной части обратится в нуль, а пространственной, наоборот, — в бесконечность! Может r = r_g это как раз тот размер объекта, когда вторая космическая скорость равна скорости света? Поэтому, давайте, продолжим мысленное сжатие, пока все вещество не станет сосредоточено в сфере, меньшего радиуса, чем гравитационный r_g.

Напомним, что гравитационный радиус пропорционален массе тела. Сжатая до гравитационного радиуса Земля была бы горошиной диаметром 1,6 см, а Солнце — шаром диаметром 6 км. После такого сжатия область в окрестности сферы радиуса r_g и все остальное пространство станут вакуумными. Это даёт возможность без помех исследовать распространение сигналов вдали от объекта и вблизи r_g, к чему мы и переходим.

Сначала разумно вернуться к «эйнштейновским» эффектам, которые мы уже обсудили в окрестности «обычных» небесных тел, таких как Солнце. Приближение к области в окрестности гравитационного радиуса делает их проявление чрезвычайно выраженным и даже парадоксальным.

Начнём с отклонения луча света. То, что с приближением к сфере радиуса r_g угол отклонения луча будет увеличиваться — вполне ожидаемо. Но до какой степени возможно это отклонение? Оказывается, при достаточном приближении луч может обогнуть объект и уйти в обратном направлении. Далее, если он будет проходить на расстоянии полутора r_g от центра, то угол отклонения станет полным оборотом. То есть в этом случае луч света

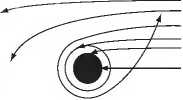
Рис. 8.1. Фотонные орбиты вокруг чёрной дыры

начнёт вращаться по круговой орбите! В отличие от орбит планет, эта орбита неустойчива — после любого незначительного возмущения луч либо покинет объект, либо «свалится» в него. Если продолжить процедуру и ещё приблизить луч к центру, то его траектория превратится в спираль, и он будет захвачен объектом.

На рис. 8.1 видно, что на расстояниях, близких к r_g фотонные орбиты как бы перепутываются. Это приведёт к странным ощущениям наблюдателя, по мере его приближения к объекту. Издалека он будет воспринимать перед собой объект как чёрное пятно, вокруг пятна — обычные созвездия, которые и были бы без объекта. Позади себя он увидит небо с обычным рисунком созвездий. Чем ближе к объекту, тем больше чёрное пятно. А на расстояниях близких к круговой фотонной орбите картина фантастически изменится. Поскольку он будет встречать лучи, которые «развернулись», то вокруг чёрного пятна вместе с прежними звёздами он увидит и звезды, которые позади него. Внутри круговой фотонной орбиты позади себя он увидит кроме обычных звёзд также и звезды, которые реально перед ним. Действительно, в этой области лучи закручиваются, разворачиваются.

Какое выражение примет эффект смещения перигелиев вблизи r_g? Изучение траекторий обычных тел с ненулевой массой покоя, пролетающих на расстояниях сравнимых с r_g, даёт ответы, похожие на описание световых траекторий. Существуют некоторые предельные параметры (зависящие от скорости), дальнейшее изменение которых определяет неминуемый захват тела, который происходит в общем случае по спирали.

Следующие эффекты — это замедление времени и гравитационное красное смещение. Явная форма решения, которое представляет геометрию Шварцшильда, позволяет легко рассказать об этом. Во всем пространстве и на подступах к сфере радиуса r_g распределим неподвижных наблюдателей. Они могут быть зафиксированы, например, с помощью ракетных двигателей, препятствующих падению к центру. У всех наблюдателей одинаковые часы, которые у каждого из них идут одинаково. Но каждая точка имеет собственное (истинное) течение времени, и в сравнении друг с другом это время течёт по–разному.

Истинное время наблюдателя на бесконечности (где, по сути, пространства–время плоское) совпадает с координатным временем t. Для геометрии Шварцшильда истинное время в каждой конкретной точке представляется выражением τ = t(g₀₀)^1/2 = t (1 — r_g/r)^1/2. Эта формула показывает, каким будет наблюдаться ход часов, помещённых в точке с радиальной координатой r удалённым наблюдателем (наблюдателем на бесконечности). То есть с его точки зрения часы, которые ближе к центру (с меньшими значениями r) идут медленнее тех, которые дальше от центра. Это, конечно, относится не только к часам, а ко всем наблюдаемым процессам. Если бы удалённый наблюдатель увидел часы в точке r = r_g то он бы констатировал, что и часы стоят, и все остальные процессы застыли! Поскольку эффект гравитационного красного смещения прямо связан с эффектом замедления времени, то чем ближе к сфере радиуса тем эффект «покраснения» сильнее. Если бы удалённый наблюдатель попытался увидеть сигнал, испущенный из точки r = r_g то он бы обнаружил, что его частота нулевая.